基于随机森林-聚类混合方法的多分类入侵检测研究

吕广旭，卢加奇，魏先燕，王小英

(防灾科技学院，河北 三河 065201)

0 引 言

随着技术手段的不断更新，传统的防御模型已无法应对当前复杂多变的网络攻击技术，以防火墙为首的防御手段正在失去“防火墙”的作用，攻击方逃逸率不断增加，它们往往采取多种攻击方式结合的手段进行，这使得精准防御逐渐变得力不从心。

随着机器学习技术的不断兴起，防火墙防御技术、入侵检测技术等有了较大进步，但仍有较大的提升空间，防御攻击能力相对较弱。网络攻击的复杂多变成为新攻击下网络安全问题不断严峻的新方向。一方面基于有监督的入侵检测方法严重依赖样本数据，样本数据分布是否合理、数据的质量成为有监督入侵检测方法应用过程中的重要一环。在数据量巨大网络环境中，数据良莠的认定成为制约有监督学习的另一关键问题，对于数据的标签处理各行业很难有统一的处理方式，导致效果未能满足要求。为此，基于无监督的入侵检测方法应运而生，无监督检测方法摒弃对样本标签数据的依赖，减少人力资源的消耗，提升了检测手段的实用价值，成为解决入侵检测重点问题的关键抓手。

1 研究概述

用于入侵检测方面的无监督方法获得了大量的关注和研究，为后续研究提供大量的理论基础。2018年，杨文君等人对于K-means聚类方法在密度、距离和阈值等方面进行了分类分析，对于各类应用场景分别进行了详细阐述。此外针对聚类方法容易陷入局部最优等实质性问题，邢瑞康等人使用数据密度等信息改进中心点依赖弊端，显著提高检测效果。入侵检测的数据往往是高维且复杂的，应对高纬度环境下压缩降维难题对于传统聚类方法难以保证检测准确率。2020年，解滨等人结合三支决策思想对传统聚类方法进行改进，消除K值对于聚类效果的限制影响，通过二次聚类手段重新划分，此方法在多攻击行为场景下表现优异。董新玉等人引入多视角余弦相似度作为衡量手段使用主成分分析对数据进行降维处理，克服有监督学习漏检率高等难题。

目前入侵检测方法存在以下关键问题：

一是传统数据降维方式中涉及较多的方式为主成分分析和线性判别分析。无论是作为无监督的主成分分析方法，还是相比较主成分分析具有较优的降维效果的线性判别方法而言，都容易存在过拟合的缺点。但不论是降维还是特征选择的方式，对原始数据的压缩和特征减少会对原始数据的表示存在损耗。因此还会出现损耗过大的情况导致误报率较高。

二是传统聚类方法存在局部最优、漏检率高、难以应对高维复杂攻击数据等主要问题，聚类算法将直接影响聚类效果的好坏。

针对上述问题，适应高维大数据检测，本文使用随机森林方法对于数据进行特征筛选以提供数据降维支撑，将特征筛选结果提供聚类方法实现多分类入侵检测效果。将改进算法应用于入侵检测分析中，其显著提升无监督聚类条件下多维数据的聚类效果，提升检测准确率。

2 随机森林-聚类混合方法

本文使用随机森林-聚类混合方法对于入侵检测数据进行分析，该方法包括两部分组成。

模型前半部分主要利用随机森林方法对入侵检测数据集进行特征筛选，对高维度数据进行降维，在尽可能最大化保留原始数据信息情况下，将数据维度降至最低。模型后半部分接受降维后的数据作为输入，使用基于改进的Canopy+K-means混合聚类方法对于数据集进行多分类划分研究。

2.1 随机森林筛选特征

由于网络流量数据的高维性，导致单独聚类方法对于入侵检测的分类效果不佳，模型的泛化能力较差。就需要前期对数据进行压缩降维处理，使提取的特征数据能够保留原始数据的大部分信息的前提下，对聚类效果进行一个更优的表达。本文使用随机森林方法对数据特征进行筛选。

随机森林筛选特征结构如图1所示，该方法将多个有监督学习模型通过一定的结合策略实现一个能力更加优秀的学习器。随机森林则是以决策树为单元划分多个单元模块分别进行决策，通过投票选择出最优的分类组合。基于随机森林的特征筛选过程则是利用随机森林基于决策树分析的这一核心思想，通过每个单元可以将特征在决策树上进行划分，对比特征对于每个树的贡献程度通常是以袋外数据错误率作为评价指标，对特征进行选取从而达到特征筛选的目的。随机森林因为随机选取初始特征性质以及强大收敛性，相比较于单个决策时进行分析时，更加适应高维数据的处理，很好避免过拟合现象发生。

图1 随机森林筛选特征结构图

2.2 Canopy+K-means混合聚类算法

传统的K-means聚类方法存在以下缺点：

（1）由于中心点的不确定性，导致簇内聚合质量较差，反映到入侵检测方面产生的直接后果影响就是具有较大的错误分类数，对于各攻击的划分非常不明确。

（2）另一方面由于聚类数据量较大，使用聚类方法计算迭代的次数也愈来愈大，导致分析时间延长。

由缺点进而演化出多种基于传统K-means聚类方法的改进方法，从密度和距离计算方式等方面进行改进，极大提高了K-means聚类方法的效果。本文使用Canopy+K-means混合算法作为改进方法，为克服K值选取的困扰，可先用Canopy算法对所选数据进行一个初期的聚类研究，根据Canopy算法的结论然后对K-means算法中的K值进行一个选取，这样既可以减少K值选取的极大不确定性，也可以减少开销时间。Canopy算法原理如下：

（1）将原始数据转换成列表形式作为样本数据，并设定初始阈值S1和S2且S1＞S2。

（2）从列表数据中随机选取样本P，计算样本数据到所有簇中心点的距离D。

（3）如果D＞S1，则形成一个新簇，将P作为新簇中心点并将P从列表中删除。

（4）如果S2＜D＜S1，则判断该样本属于该簇并将其从列表中删除。

（5）如果D＜S2，则该点于该簇中心距离相当近属于强相关，并将其从列表中删除。

（6）直至列表为空结束循环。

3 实验分析

3.1 实验环境和数据

为验证随机森林-聚类混合方法的多分类入侵检测方法的应用效果，本文采用数据为CSE-CIC-IDS2018流量数据集，该数据集主要用于评估和测试入侵检测系统，包括Bruteforce、Heartbleed、Botnet、DoS、DDoS等七种攻击场景，由470台计算机和30台服务器组成的攻防网络中。该流量数据集包含正向数据包总数、数据包平均大小、在向后方向传输的数据包中设置 URG 标志的次数（对于UDP为0）、数据流的平均长度等共80多个特征。

实验环境为LINUX操作系统，Intel CPU、RTX3090 GPU，64 GB内存，运行环境为Python3.6。

为了验证聚类方法在数据集上的实验效果，本文采用调整互信息（AMI）、调整兰德系数（ARI）和准确率三个做为聚类方法“外部”和“内部”性能度量的评价指标。具体如下：

（1）调整互信息是基于互信息的优化，用于评价随机变量之间的关联信息，调整互信息值越大则表明聚类结果和实际分类结果越相近。

（2）ARI调兰德系数是基于兰德系数的优化，评价随机变量之间的划分的重叠程度，结果越接近1，则聚类结果越优秀。

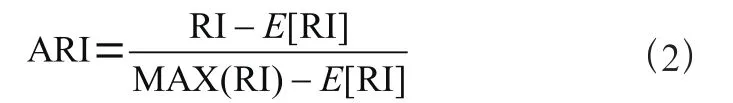
（3）准确率为正确聚类样本数/入侵检测样本数。

3.2 实验结果分析

使用数据集对于首先对于随机森林-聚类混合方法进行分析，并对比单独K-means方法、Agglomerative层次聚类、DBSCAN密度聚类方法进行对比实验，对比不同方法期望验证提出方法的有效性。首先用ids2018数据进行分析，用于随机森林算法对于数据特征进行筛选，使用重采样方法将数据进行划分，对于特征重要性进行排序。

首先对数据集进行预处理，将无效数据和空数据进行替换和删除，同时发现部分数据集的特征值全为零值，对聚类方法效果无影响，因此删除这些特征。使用随机森林作用于数据集进行特征筛选后的结果如表1所示，我们选取阈值大于0.02为有效特征，共计15个特征作为后续聚类分析的输入。

表1 有效特征及重要性

使用Canopy进行粗聚类研究，根据指标调兰德系数分析，当聚类数在7～8之间时，系数值高于其他聚类数，如图2所示。与数据集描述七种攻击场景和一种正常环境也相符合，因此选取初始值为8。

图2 Canopy不同簇数下的ARI值

将聚类K值给定K-means聚类方法进行聚类分析，并对比不同聚类方法的实验效果，实验效果如表2所示。

表2 不同算法在数据集上的实验效果

实验结果表明，传统聚类方法在2018检测数据集中检测效果差距不大，其中层次聚类方法相较于K-means方法和DBSCAN检测方法，在各项指标表现较优，改进后的随机森林-聚类混合方法在入侵检测数据集表现各项指标均优于传统聚类方法，相对于传统方法中表现优越的层次聚类方法，准确率提升了19.6%，同时AMI和ARI指标均大幅度改善，表明该方法簇内和簇间的聚类划分能力强，极大改善了传统入侵检测方法的检测效果。

4 结 论

入侵检测是防御网络攻击中重要一环，为了解决传统聚类检测方法误报率较高，难以应对高维数据分析等关键难题，本文提出一种基于随机森林-聚类混合方法的多分类入侵检测方法，该方法基于CSE-CIC-IDS2018流量数据集，使用随机森林进行特征筛选和组合，然后将筛选后的特征输入聚类算法中，该聚类方法结合Canopy和K-means算法进行，可大幅度减少开销时间，使K值确定更加准确，先用Canopy算法对于数据进行粗聚类为K值大小提供参考依据，然后使用K-means聚类方法进行多聚类划分。实验结果表明，该方法能够有效处理高维数据环境下入侵检测数据，相比较于传统聚类方法，各项指标更高，检测效果更加优越。