动量定理在Unity 3D中的应用

丁彦希，张迪迪，徐秋雨，郭仁春

（沈阳化工大学，辽宁 沈阳 110142）

0 引 言

动量定理是动力学的普遍定理之一。刚体是力学中的一个科学抽象概念，即理想模型。Unity 3D简称U3D，是由Unity Technologies公司开发的一个让玩家轻松创建诸如三维视频游戏、建筑可视化、实时三维动画等类型互动内容的多平台的综合型游戏开发工具。在U3D中，是通过物理引擎机制来实现物体的物理效果。物理引擎通过为刚性物体赋予物理属性的方式来模仿真实世界中的物体碰撞、跌落等反应。本文通过给刚体添加力和力矩来使刚体产生运动，包括平动和转动，并对运动状态进行定量分析，使读者能更好的认识动量定理在刚体运动中的体现，从而更好地设计一个仿真系统。

1 刚体运动——从刚体平动到刚体转动

1.1 牛顿定律和动量定理

刚体都有质心的概念，如果作用力的方向通过质心，则可以将刚体视作质点。当刚体的作用力不在质心上时，刚体会发生转动，转动时所有的物理量和物理定律都可以从平动形式类推过来。

刚体平动用位移，速度，加速度，惯性，力，动量，冲量等描述，对应的刚体转动要换成角位移，角速度，角加速度，转动惯量，力矩，角动量，角冲量等概念，所有的物理定律都不变，如表1所示。

表1 刚体平动与刚体转动物理量对比

1.1.1 平动惯性定律和转动惯性定律

牛顿第一定律也叫惯性定律，惯性是物体要保持原有的状态。惯性是有大小的。物体的质量mass就是衡量惯性的一个重要指标。

转动时，物体要保持匀速旋转的状态，即保持角速度大小和方向不变，这就是转动惯性定律。转动惯性也有大小，用转动惯量来衡量。转动惯量用I来表示，其定义为

其中是质量，是该质心的位置到转轴的距离，的单位是kgm。

1.1.2 平动牛顿第二定律和转动牛顿第二定律

如果要改变状态就需要外力。外力越大状态改变也越大，但如果惯性即质量很大，状态改变就越小。用数学公式来描述即

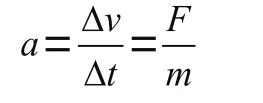
这就是牛顿第二定律，其中是惯性，是外力，是加速度。

如果要改变转动的状态，即改变角速度，就需要对刚体加外力矩，因此角速度的改变用角加速度来衡量，该值与外力矩大小成正比，与转动惯量成反比，这与加速度的定义极为相似，即：

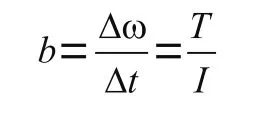
1.1.3 平动动量定理和转动动量定理

平动过程中的动量是，转动过程中的角动量是。平动的动量定理和转动的角动量定理分别为：

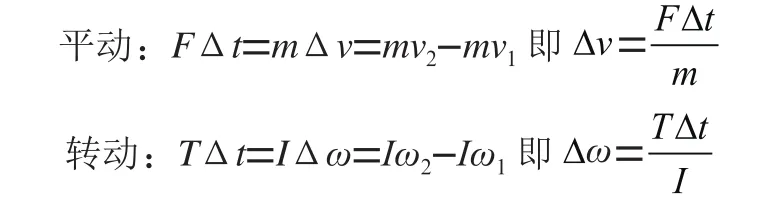
1.1.4 动量守恒和角动量守恒

当两个物体相互碰撞后，在没有损耗的情况下，碰撞前的总动量=碰撞后的总动量，这就是动量守恒。与平动相似，角动量也满足守恒定律。如果两个刚体相碰撞，两者相比较如下：

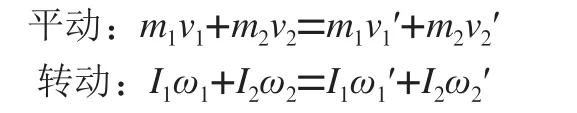
这些定律都体现在U3D的物理引擎中，了解这些物理定律就会让虚拟仿真更符合的预期。

1.2 刚体属性

在场景中放置一个平面Plane作为地面，再添加一个立方体Cube和一个球体，并让这两个物体位于地面上方如图1（a）所示。给立方体和球体增加刚体组件RigidBody如图1（b）所示。运行后物体会自动落到地面。

图1 Rigidbody组件

让场景中的物体运动可以有两种方式，其一是运动学，其二是用物理学。

运动学使用的是物体的Transform，直接用Translate（平移）和旋转（Rotate）来使物体移动或旋转，或者直接用代码改变物体的位置和欧拉角。

场景中的物体加载了Rigidbody组件，就要受到物理定律的控制，如果希望不被物理定律控制，可以开启该组件中的Is Kinematic选项。

与物理问题相关的程序要写在FixedUpdate中，FixedUpdate两帧之间的间隔是固定的，默认是0.02 s，也就是1秒钟运行50次。这与Update不同，Update两帧之间的间隔是不固定的。

质量mass（kg），速度velocity（m/s）是刚体的两个基本属性，一个代表惯性，一个代表状态。在刚体的众多属性中最重要的就是速度velocity了，而mass多数时候可以忽略。

2 转动惯量inertiaTensor

对于平动，刚体有一个惯性量就是质量mass，同样对于转动，刚体也有一个描述转动惯性的量，叫作惯性张量inertiaTensor。

转动惯量除了与质量相关外还与旋转轴位置、刚体形状和大小有关。同一个刚体旋转轴的位置，有不同的转动惯量。若旋转轴通过刚体的质心，轴的方向不同，也会有不同的转动惯量，其中沿着物体坐标系，，主轴的三个方向的转动惯量最为重要，其次是其他方向，这样的转动惯量共有9个参数形成一个张量矩阵如下：

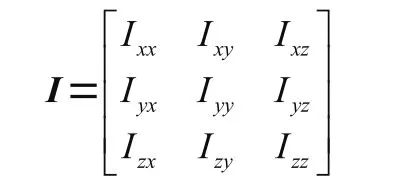
，，主轴方向上的量处于矩阵的对角线上，即I，I和I。在U3D中，惯性张量inertiaTensor就是指这三个数，形成一个向量。

3 AddForce

将场景中物体的质量mass设为2 kg，给刚体施加一个沿轴方向500 N的力的代码如下：

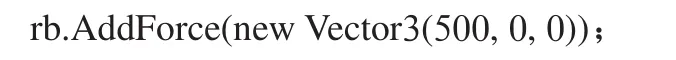
其中，rb是指如图1所示场景中的物体。

像平时扔东西，击球或开枪都是给物体一个初始的力，然后物体就沿力的方向前进了。但同样是给物体一个水平方向500 N的力，瞬间给一下，持续一段时间和一直持续给，物体速度很显然是完全不同的。如下文给出的代码所示：

其中AddForce代码只在Start()中仅加载一次，AddForce是对物体加力，这个力的作用时间Δ其实就是0.02 s，也就是FixedUpdate两帧之间的间隔Fixed Timestep。

根据动量定理求出：

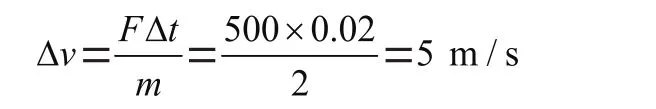
U3D中对AddForce提供了四种模式，用ForceMode来区别，方法是对AddForce增加第2个参数：

rb.AddForce(new Vector3(500, 0, 0), ForceMode.Force);

ForceMode的四种模式分别是：Acceleration、Force、Impulse、VelocityChange，其力的作用方式有些区别，默认是Force，可以省略。

3.1 Force

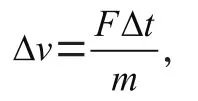
3.2 Acceleration

Acceleration是加速度，单位是m/s，加速度本身就是速度的改变量，因此下面的代码：

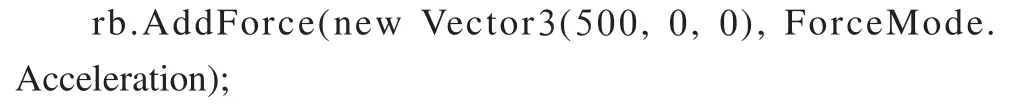
可以猜测得到物体的速度应为：10 m/s

因为加速度=500 m/s，说明速度1秒增加500 m，因而作用时间是0.02 s，最终速度自然就是500×0.02=10 m/s。

由于直接使用的是加速度，就不用考虑物体质量了。

3.3 Impulse

Impulse是冲量，单位是N•s或者kg•m/s，该量就是直接给了Δ。因此下面的代码：

rb.AddForce(new Vector3(500, 0, 0), ForceMode.Impulse);

可以猜测到物体的速度为：

由于直接给的是冲量，这样就不用考虑作用时间0.02 s了。因此Impulse应该是每次运行就施加500 N•s，与作用时间无关，只考虑运行次数即可。

3.4 VelocityChange

VelocityChange 顾名思义是速度的改变量，这样的说法有点类似Acceleration，与Acceleration不同的是，VelocityChange是每次运行就改变速度的量，而Acceleration则是每秒速度的改变量。因此VelocityChange的单位应该是米/秒/次。

因此代码：

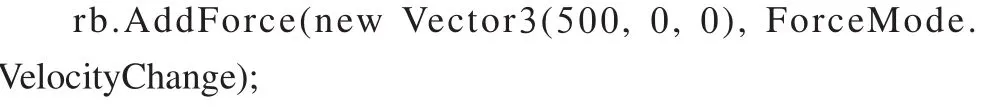
运行结果就应该是：500 m/s

VelocityChange与Acceleration一样不用考虑物体的质量。VelocityChange与Inmpuse一样不用考虑那个时间间隔。

通过这几个例子可以看到velocity才是最想知道的量，而mass常被忽略。

4 AddTorque

4.1 给立方体加力矩

与AddForce相似，可以给物体施加力矩AddTorque，该力矩可以使刚体绕质心旋转。如果外力矩为，则刚体的角速度的变化量为：

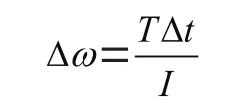
在U3D中Δ=0.02 s，为转动惯量，这个转动惯量为惯性张量inertiaTensor，由于是张量，问题就变得比平动复杂得多，下面依然采用手工计算与代码相结合的形式进行相互验证。

对场景中的立方体编写下文的代码：

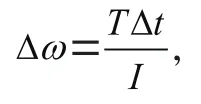
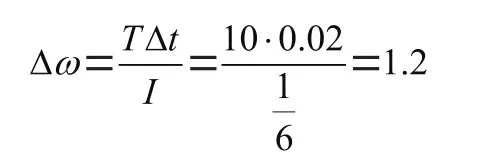
因此结果应该是（1.2，0，0）。运行后发现正是这个结果如图2所示。

图2 给立方体加力矩后的运行结果

4.2 给长方体加力矩

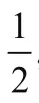
通过代码验证，结果如图3所示。

图3 长方体的转动惯量运行结果

下面将长方体斜着放置，力矩仍保持不变，将立方体的欧拉角设为（0，30，0），如图4（a）所示是顶视图。现在给一个力矩=(10，0，0)，这个力矩是对世界坐标系的而言的。那么认为物体应该绕世界坐标x轴旋转，即如图4（b）所示的那个样子，绕红色轴旋转。

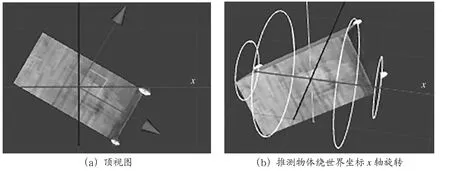
图4 斜长方体方体转

然而运行结果却是另外的形式，转轴相对世界坐标发生了偏移，其角速度如图5所示。

图5 运行结果

如图6（a）所示，物体是绕着黄色的轴旋转的，不是红色的轴

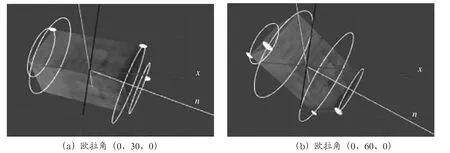
图6 对x轴加力矩，结果旋转轴发生偏移

如果再将欧拉角改成（0，60，0），结果如图6（b）所示的样子，其角速度如图7所示。

图7 运行结果

本来是给世界坐标系的轴施加力矩，实际上物体却没有绕世界坐标系的轴旋转而是发生了偏移，角速度为（1.02，0，-0.312）。

4.3 ForceMode

AddTorque与AddForce一样也有ForceMode选项，包括 Acceleration，Force，Impulse，VelocityChange，含义也都与AddForce中一样，只不过这几个量改变的是角速度，默认Force可以省略，具体如下文给出的代码所示：

含义是对角速度的改变量为10 rad/s，可以推知，作用时间为0.02 s时速度的改变量为0.2 rad/s，不 用考虑转动惯量。

ForceMode.Impulse是冲量，需要考虑转动惯量：

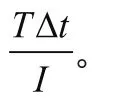
ForceMode.VelocityChange是每次直接改变角速度，不用考虑转动惯量，代码为：

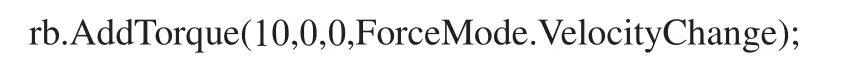
5 结 论

动量定理是物理学中的一个基本规律。在Unity3D中，动量定理在刚体运动过程中充分体现，基于此定理的基础上可以计算出物体的运动状态，从而使用户更精确地去控制虚拟物体的运动。