高功率因数谐振式无桥型LED 驱动电源

黄 聪，曹克煜，刘雪山，周 群，贺明智

（四川大学电气工程学院，成都 610065）

随着AC-DC 开关变换器的大量使用，其向电网中注入的谐波电流已经成为电网中最主要的谐波污染源之一。为减少电力电子设备对电网的谐波污染，欧盟的IEC 61000-3-2 Class C、中国的GB/T 14549—93《电能质量公用电网谐波》 等标准对电力电子设备输入电流的各次谐波提出了限制要求[1]。功率因数校正PFC（power factor correction）技术可以有效减小输入电流谐波，提高电力电子设备的功率因数，因此在LED 驱动电源等领域中得到了广泛应用[2-3]。

传统的AC-DC LED 驱动电源需要在交流输入端加整流桥[4-7]，这增加了驱动电源的导通损耗，降低了效率。为解决这一问题，许多学者对无桥PFC变换器展开了研究[8-11]。文献[9]提出了一种反激类无桥PFC 变换器，该变换器为了防止输入能量向输出直通，需要设置较大的变压器匝比，进而增加了有源开关的电压应力。文献[10]提出的Boost 类无桥PFC 变换器无法实现降压输出，限制了其单级PFC 应用。文献[11]提出了一种无桥功率因数校正变换器，该变换器利用拓扑的双极性增益特性实现了无桥输入，但该变换器仅能实现单路输出，无法实现多路均流输出，限制了其在大功率LED 驱动等领域的应用。

本文在文献[4]的基础上提出一种高功率因数谐振式无桥型LED 驱动电源。该驱动电源利用谐振网络实现正负极性增益，进而实现无桥输入，降低驱动电源的导通损耗。同时，利用谐振电容的电荷平衡实现各输出支路均流，解决并联LED 串的均流驱动问题。该驱动电源中的双向有源开关仅采用一个控制信号，简化控制电路。本文对该LED 驱动电源的工作模态及工作特性进行理论分析，最后搭建一台98 W 的实验样机验证该驱动电源拓扑结构的可行性和有效性。

1 工作原理分析

本文所提出的谐振式无桥型高功率因数LED驱动电源的主电路及其控制电路如图1 所示。主电路由输入LC 滤波器、变压器T（等效成由励磁电感Lm、理想变压器、漏感Lk组成）、双向开关S1、S2、谐振电容Cr、二极管D1、D2、输出电容C1、C2及负载LEDs1、LEDs2组成。此LED 驱动电源采用恒定导通时间COT（constant on-time）控制，用于实现功率因数校正与输出电流的控制。通过控制环路，输出支路1 的电流io1被调节为Vref/Rs，其中Vref为控制环路的参考电压，Rs为输出电流的采样电阻，从而实现恒流输出。利用谐振电容Cr的电荷平衡可实现支路1 和支路2 的均流输出，因此通过控制支路1的电流恒定即可实现对支路2 电流的恒流控制。

图1 LED 驱动电源及其控制电路Fig.1 LED driver and its control circuit

2 工作特性分析

2.1 工作模态分析

为了简化分析，先做出如下假设：

（1）输入电压Vin（t）=Vmsin（ωt），Vm为交流电压幅值，ω 为交流电压角频率；电网工频周期T 远大于变换器开关周期Ts，即T ≫Ts；输入电压在一个开关周期内可近似不变。

（2）变压器由励磁电感Lm、匝比为np∶ns=1∶n 的理想变压器和二次侧漏感Lk组成，其中Lm≫Lk。

（3）谐振电容Cr远小于输出滤波电容C1和C2。令C1=C2且输出滤波电容足够大，使输出电压保持不变。两路LED 负载参数相同。除了变压器以外，所有电子元件都是理想的，忽略其寄生参数影响。

由于所提驱动电源相对于交流输入的正负半周具有对称的电路结构，因此，在交流输入电压的正负半周，驱动电源的工作模态类似。在此仅对输入电压正半周的工作模态进行分析。

图2 为所提驱动电源工作在断续导通模式DCM（discontinuous conduction mode）下的主要波形，其中t0～t2对应d1Ts，t2～t3对应d2Ts。在一个开关周期Ts内，该LED 驱动电源存在4 个工作模态，对应的模态电路如图3 所示。

图2 所提LED 驱动电源的主要波形Fig.2 Key waveforms of the proposed LED driver

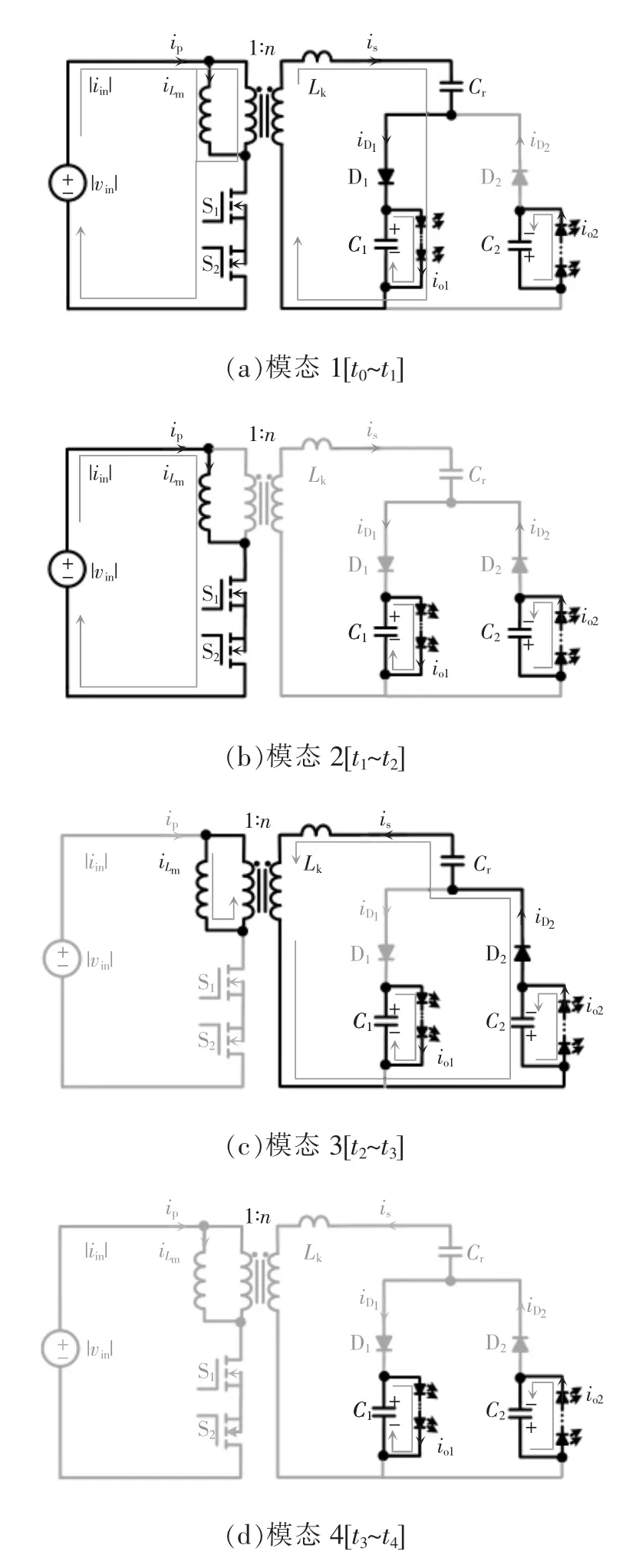
图3 各模态的等效电路Fig.3 Equivalent circuits in different modes

模态1[t0～t1]：t0时刻，开关管S1、S2导通，输入电压加在励磁电感Lm上，励磁电感电流iLm线性上升。变压器二次侧漏感Lk和谐振电容Cr开始谐振，二极管D1因承受正向电压而导通，电容C1提供电压Vo1给LED 供电。在开关周期开始时刻，励磁电感电流iLm=0，可得

式中：VCr为谐振电容电压；ΔVCr为谐振电容电压的幅值；；iD1为二极管D1的电流。

可得一次电流ip为

模态2[t1～t2]：t1时刻，开关管S1、S2继续导通。二极管D1的电流iD1谐振到0，实现了零电流关断ZCS（zero current switching），此时一次电流ip=iLm，继续线性上升，输出电容C1足够大，继续给LED 供电，谐振电容电压VCr保持t1时刻的电压不变，则有

模态3[t2～t3]：t2时刻，开关管S1和S2关断，为保持励磁电感电流iLm的流通路径，理想变压器和二极管D2、谐振电容Cr及输出电容C2为其提供通路，二次电流is反向下降到0，D2实现了ZCS。又因为折算到二次侧的励磁电感n2Lm≫Lk，此时is反向线性下降到0，则有

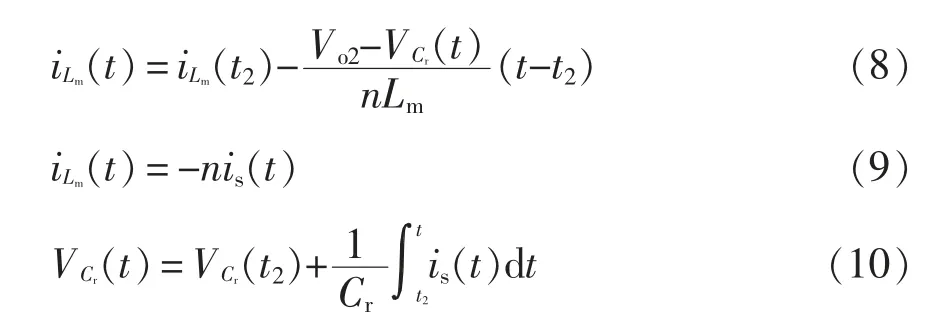
根据式（8）和（9）可得

式中，iD2为二极管D2的电流。

由图2 和图3 可知，谐振电容Cr在模态1 充电、在模态3 放电。根据电容电荷平衡原理，在一个开关周期内Cr的电荷量之和为0。由此可得

式中，Qch、Qdis分别为Cr的充电电荷量和放电电荷量。

根据式（3）和式（11）可以推导出其变化量ΔVCr为

式中：d1为开关管S1、S2的导通占空比；d2为二极管D2的导通占空比。

模态4[t3～t4]：t3时刻，ip和is均减至0，因为输出电容C1和C2足够大，保持输出电压Vo1和Vo2不变继续给LED 供电至t4时刻。t4时刻，该模态结束，开始下一个开关周期。

由以上模态分析可知，该LED 驱动电源无论是交流正半周输入，还是交流负半周输入，负载端均可以实现正电压输出，因此该LED 驱动电源具有正负极性增益特性，进而实现了变压器原边无整流二极管的拓扑结构。

2.2 输出支路均流特性

谐振电容Cr在模态1 充电、在模态3 放电。根据电容电荷平衡原理，在一个开关周期内Cr的充电电荷量Qch和放电电荷量Qdis之和为0。由此可得在一个开关周期内流过二极管D1、D2的平均电流iD1-avg、iD2-avg相等，即有

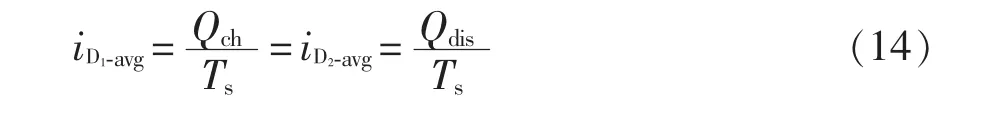
由式（1）、式（6）、式（11）可以进一步求得一个开关周期内流过二极管D1、D2的平均电流为

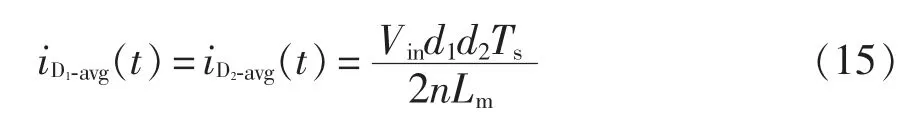
由励磁电感Lm伏秒平衡可得

式中，VCr-avg为谐振电容电压的平均值。

由式（2）、式（7）、式（10）可得，模态3 中谐振电容电压平均值VCr-avg为

将式（16）代入式（17）中可得

将式（18）代入式（15）可得

由此可得输出电流表达式为

利用Matlab 的曲线拟合，可得其近似等式为

将式（21）代入式（20）中，可以得到半个工频周期内输出电流表达式为

根据式（22）可知，输出电流io1=io2，即利用谐振电容Cr的电荷平衡实现了支路1 和支路2 的均流输出，因此通过控制支路1 的电流恒定即可实现对支路2 电流的恒流控制。

2.3 谐振电容的选取

将式（22）化简可得

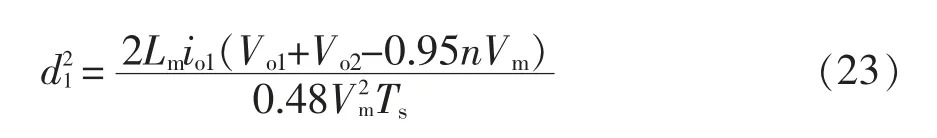
根据模态分析可知，要使二极管D1在模态1实现ZCS，需要满足2d1-minTs＞Tr，这里d1-min为最大输入电压时对应的最小占空比，Tr为谐振周期，将其化简可得

将式（23）代入式（24）中可得

式中，Vm-max为Vm的最大值。

根据模态分析可知，当开关管关断时，要使模态3 中变压器励磁电感复位，需满足Vo2-VCr-max（t）＞0，因为在t2时刻VCr（t）满足最大，则可得

将式（13）、式（18）、式（23）代入式（26），可得

将参数Lm=420 μH，Lk=1 μH，Vm-max=339.36 V，Vo1=Vo2=70 V，io1=0.7 A，n=1/3,Ts=20 μs，π=3.14 代入式（24）和式（27）中，可以得到330 nF＜Cr＜680 nF。

2.4 输出电容的选取

假设变换器的传输效率为100%，则输入功率等于输出功率。由瞬时功率平衡原则，可得

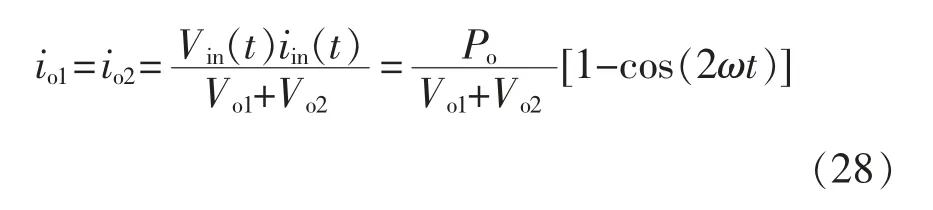
式中，Po为输出功率。式（28）包含2 倍工频的交流分量，可以求得输出纹波电压vrip表达式为

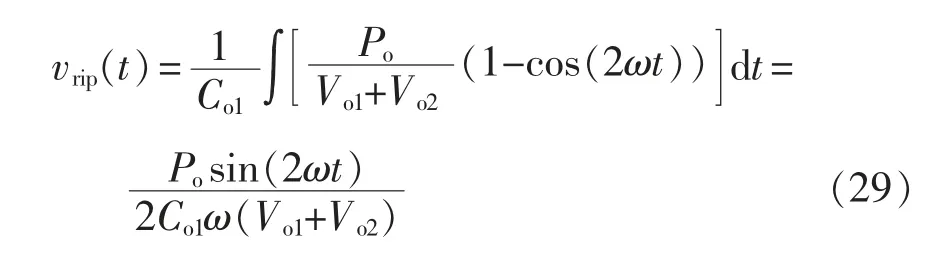
由式（29）可得，输出纹波电流irip表达式以及输出滤波电容表达式为

式中，Δvrip-pp为输出电压纹波的峰峰值，取Δvrip-pp为5 V，代入相应参数到式（31）中，最终选择电解电容容值为660 μF。

2.5 输入电流

图4 为该LED 驱动电源在一个工频周期T 内的关键波形。

图4 一个工频周期内LED 驱动电源关键波形Fig.4 Key waveforms of the proposed LED driver in one line cycle

以工频交流正半周输入为例，结合第2.1 节工作特性分析可知，在一个Ts内，变压器一次侧电流平均值ip-avg由励磁电感电流与次级电流耦合到初级的电流叠加而成，其表达式为

将式（1）、式（3）、式（6）、式（13）代入式（32）中，可得

将式（18）代入式（33），在T/2 内输入电流为

图5 给出了半个工频周期内不同α 取值下输入电流的变化曲线。由图5 可知，当α 取值越小，输入电流正弦度越高，相应功率因数越高。

图5 α 对输入电流iin 的影响Fig.5 Effect of α on input current iin

2.6 效率理论分析

同文献[4]提出的电路拓扑相比，本电路拓扑在变压器一次侧减少了整流桥，增加了一个开关管，变压器二次侧结构相同。因此仅对一次侧的整流桥和开关管的导通损耗做出理论分析。

在一个Ts内，由变压器一次电流引起的整流桥导通损耗Pbr-i为

式中，Vbr为整流桥二极管的导通压降。将式（18）、式（23）代入式（35）中，可得在半个工频周期内整流桥的导通损耗Pbr为

在一个Ts内，由变压器一次电流引起的开关管导通损耗Pmos-i为

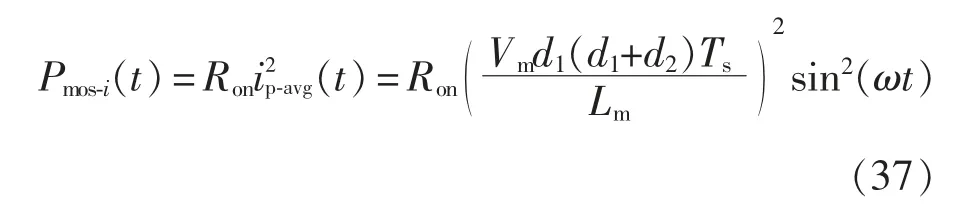
式中，Ron为开关管的导通电阻。将式（18）、式（23）代入式（37）中，可得T/2 内开关管的导通损耗Pmos为

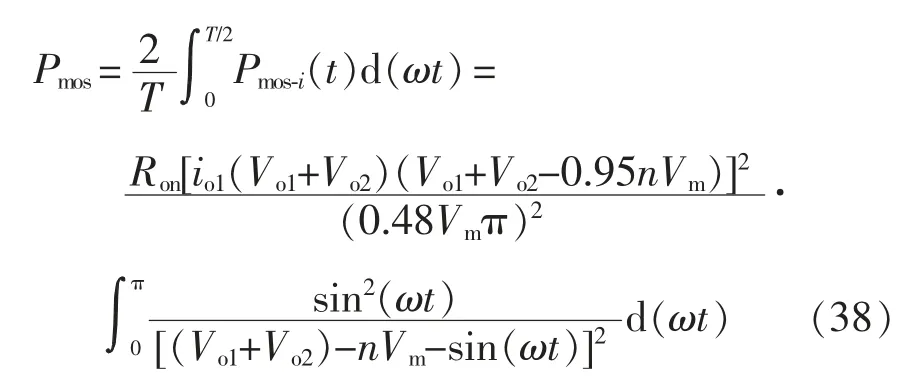
由式（36）和式（38）可知，当输出电压和输出负载不变，即输出功率不变时。整流桥和开关管的导通损耗主要由输入电压决定，输入电压越低，导通损耗越大，效率越低；输入电压越高，导通损耗越低，效率越高。在110 V 交流电压输入时，将Vbr=0.6 V、Ron=0.65 Ω、Vo1=Vo2=70 V、io1=0.7 A、π=3.14 代入式（36）和式（38）中，可以得到Pbr≈1.17 W、Pmos≈0.59 W，整流桥和开关管导通损耗相差0.58 W。

2.7 拓扑结构拓展

利用谐振电容的充放电平衡原理，添加相应的均流支路到本文提出的高功率因数谐振式无桥型LED 驱动电源拓扑中，便可拓展得到n 路输出的无桥LED 驱动电源拓扑，其拓扑如图6 所示。

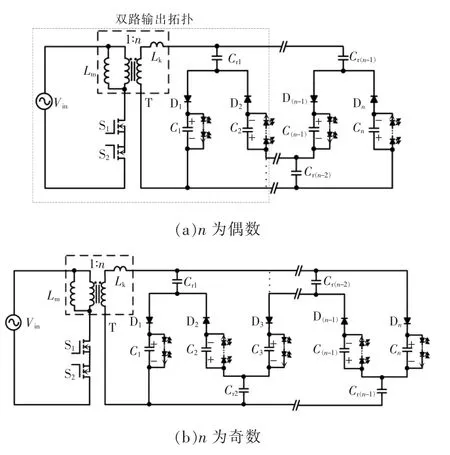
图6 n 路输出无桥LED 驱动电源拓扑Fig.6 Topology of multi-output bridgeless LED driver

3 实验验证

为了验证上述理论分析的正确性及可行性，搭建了一台98 W 实验样机，如图7 所示。该样机输入交流电压为100～240 V；两路输出均为70 V/700 mA；有源开关管S1、S2型号为15N65；变压器型号为PQ3525、Lm=420 μH、Lk=1 μH、np∶ns=3∶1；Cr为470 nF/100 V；二极管D1、D2型号为ES5J；每路输出采用2个330 μF/100 V 电解电容并联滤波；控制芯片采用FL6961；误差放大器采用TSM103。

图7 实验样机Fig.7 Experimental prototype

实验样机关键测试波形如图8 所示。

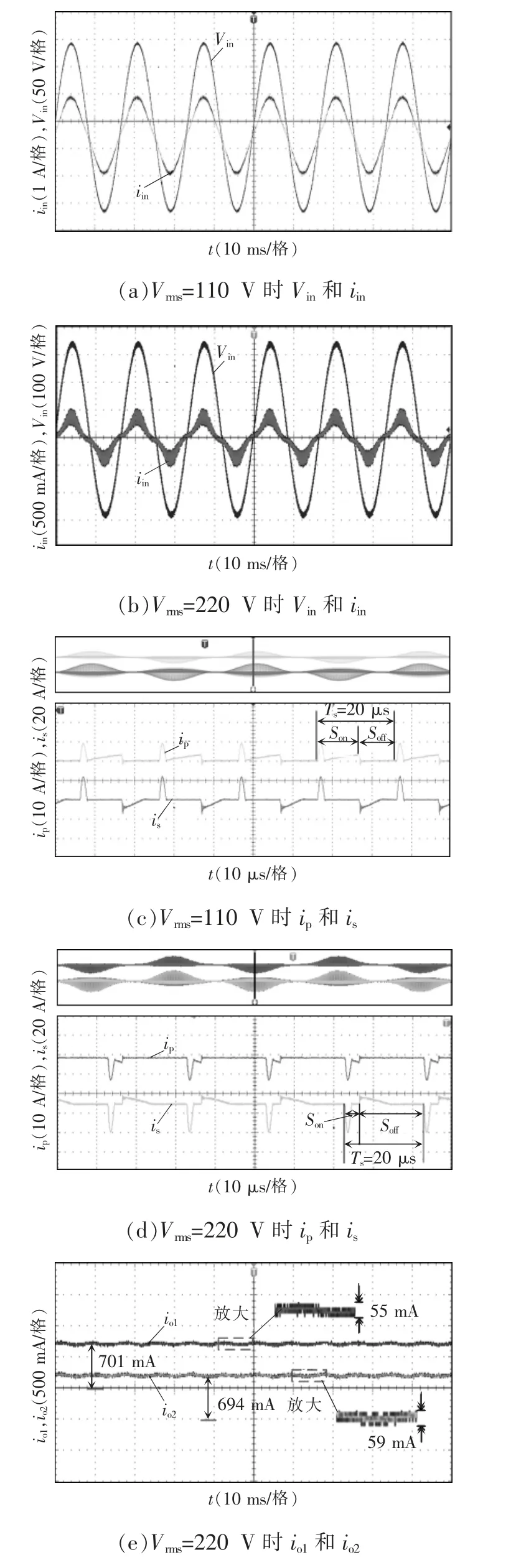
图8 实验样机关键测试波形Fig.8 Key test waveforms of prototype

图8（a）和（b）分别为输入电压有效值Vrms110 V和220 V 输入电压Vin和输入电流iin波形，可以看出iin跟随Vin保持同相位，说明该电源具有较好的功率因数校正功能。结合第2.3 节分析可知，当输出电压不变，输入电压110 V 比220 V 低，相应α 也低，因此输入电压110 V 对应的iin正弦度越高，功率因数也越高；图8（c）和（d）分别为Vrms110 V 和220 V 时，该变换器工作在DCM 模式下的变压器一次侧电流ip和二次侧电流is的波形。可以看出，Ts为20 μs，开关管导通时间和输入电压大小有关，输入电压越低，开关管导通时间越长。图8（e）为Vrms220 V 时两路LED 负载的稳态电流波形，可以看出两路电流较好地实现了均流输出。

在本台实验样机平台基础上，通过增加整流桥和减少开关管，采用相同的控制方式以及输入输出规格，比较文献[4]所提LED 驱动电源和本文所提无桥LED 驱动电源功率因数和效率。2 种变换器的PF与效率随输入电压变化的曲线对比如图9 所示。

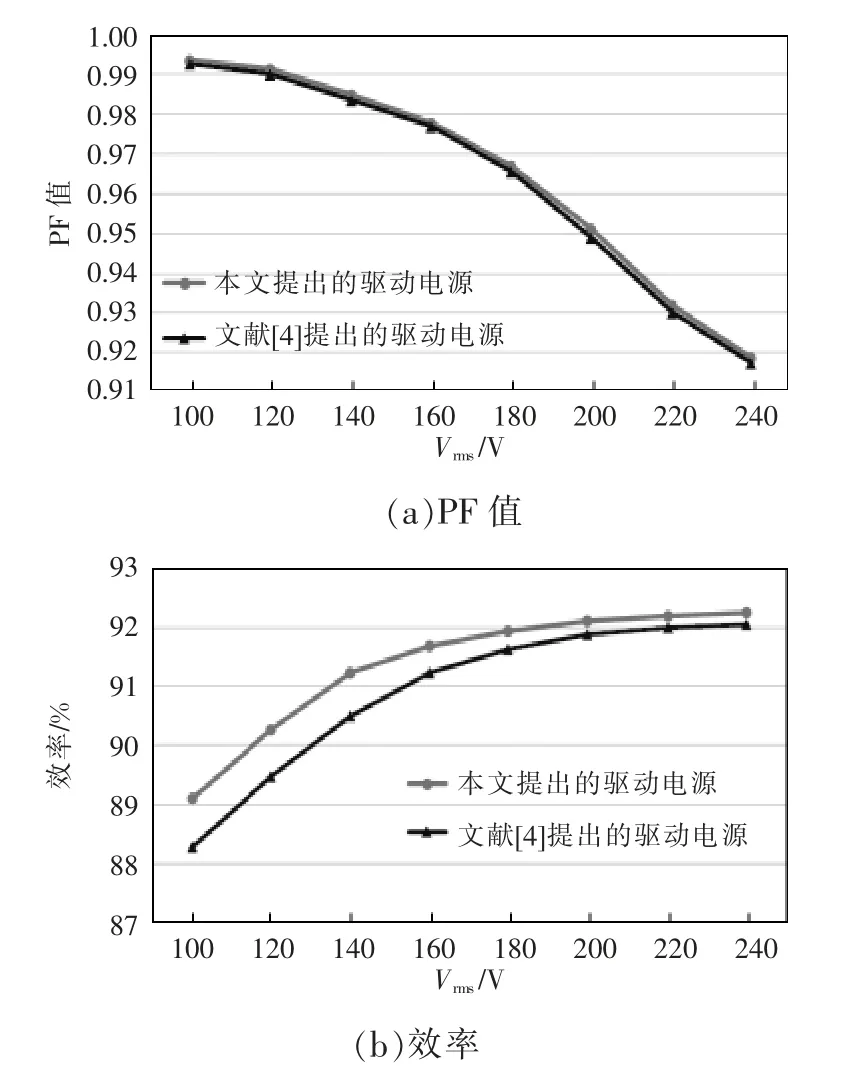
图9 PF 值与效率随输入电压变化的曲线Fig.9 Curves of PF and efficiency against input voltage

由图9 可知，本文所提LED 驱动电源功率因数接近于文献[4]所提LED 驱动电源，而效率明显高于文献[4]所提LED 驱动电源。当输入110 V 时，由第2.6 节理论推导得出本文所提驱动电源比文献[4]所提驱动电源的功率损耗低0.58 W，实际测量值也比较符合，验证了理论推导的正确性。

4 结语

本文在文献[4]的基础上提出了一种高功率因数谐振式无桥型LED 驱动电源，该驱动电源利用谐振网络实现了正负极性增益，消除了交流输入端的整流桥，降低了变换器的导通损耗。同时，利用谐振电容电荷平衡实现了各输出支路均流，解决了并联LED 串的均流驱动问题。本文所提驱动电源中的双向有源开关仅采用一个控制信号，简化了控制电路，具有结构简单、输出升降压、电气隔离等优点。详细分析了该驱动电源工作在DCM 模式的工作模态和工作特性，最后搭建了一台98 W 的样机进行实验验证，实验结果验证了该驱动电源拓扑结构的可行性和有效性。