预应力模态下对旋风机叶片流致振动特性
姜 华,常越勇,宫武旗,张子惠
(1.西安科技大学 能源学院,西安 710054;2.西安交通大学 能源与动力工程学院,西安 710049)
0 引言
对旋风机由于流量大、反风性能好、反风效率高而广泛应用于矿山、隧道、地铁等特殊空间的通风系统[1-2],实际运行过程中对旋风机流场非定常气动激励作用会施加于叶片表面,当激振力的频率等于或是接近叶片固有频率时,很容易引起叶片的共振,严重时会引起叶片的断裂[3-4],因此有必要深入分析对旋风机非定常激励力作用下叶片的动力学特性。但目前有关对旋风机的研究多针对改变叶顶间隙[5-6]、叶片形状[7-8]、转速匹配[9-10]、轴向间距[11-12]、进口畸变[13]等参数来研究风机流场性能或者气动噪声特性,有关对旋风机运行过程叶片流致振动特性的研究鲜少涉及。
模态分析法是叶片动力学分析的基础[14-16],国内外学者采用模态分析法针对风机叶片共振预测、振动原因分析、叶片优化设计、疲劳失效位置定位等方面进行了大量研究。杨冰冰等[17]通过计算对旋风机叶轮模态固有频率预测共振,发现叶轮固有频率避开了电机的频率,在正常工作时不会产生共振。吴娟等[18]对叶片可调式对旋风机进行了叶轮模态及振动试验,结果表明风机低频处振动主要由自身结构问题引发,而高频激振处的振动主要由气流的压力脉动造成。王瀚艺等[19]对故障叶片进行模态应力、振型分析,提出一种改型叶片,避开了故障叶片的事故频率,使用过程中未发生断裂现象。RANI等[20]通过从燃气轮机叶片结构频响函数中提取模态特性,来进行失效模式检测和裂纹定位,显示叶片在6阶模态频率处发生共振,导致叶片失效,且失效叶片计算模型的应力集中区域与现场采集的实际失效叶片裂纹区域得到了验证。然而,上述研究多以自由模态作为风机运行时的实际模态,忽略了风机在运行过程中离心力、气动力这两种预应力作用对于结构模态的影响,这会造成基于模态结果分析叶片动力学特性时产生较大误差,使结果不够精确。
基于此,本文以对旋风机叶片为研究对象,考虑到实际运行中叶片受到预应力的影响,采用基于预应力模态的强迫振动响应分析方法,定量研究了对旋风机非定常气动力激励下叶片的动力学特性,同时对比了无预应力模态和预应力模态下的叶片监控点的振动加速度响应曲线及总振动加速度级,为后续对旋风机叶片的减振优化提供理论依据。
1 数值计算方法
1.1 流场计算设置
本文研究的旋风机设计参数[21]为:流量Q=44 000 m3/h,功率P=55 kW,转速n=2 950 r/min,进口压力Pin=101 325 Pa,出口静压Pst=6 400 Pa,一级、二级叶轮叶片数分别为Z1=15,Z2=10。通过风机设计数据建立对旋风机几何模型如图1所示。
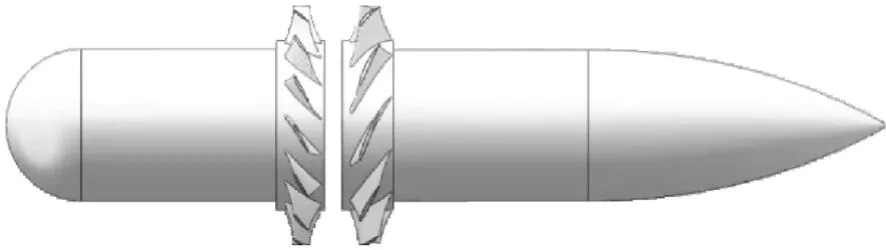
图1 对旋风机几何模型Fig.1 Geometric model of a contra-rotating fan
首先进行网格无关性验证,由图2可知,随着网格数的由70万增加到145万时,对旋风机的压升、效率曲线保持稳定,由此确定对旋风机单流道网格数目为145万。非定常流场计算,边界条件设置为质量流量进口,压力出口,交界面采用滑移网格模型,湍流模型采用大涡模拟,采用PISO算法求解,时间步长设置为4.52×10-5s。

图2 流场网格无关性验证Fig.2 Grid independence verification of flow field
1.2 预应力模态设置
未考虑预应力时叶片结构模态分析控制方程为:

式中 [K]——结构刚度矩阵;
ω——为结构的圆周频率;
[M]——结构质量矩阵;
φ——为特征向量,即结构振型。
实际风机运行中主要受到离心力和气动力两种预应力载荷的作用,叶片预应力模态分析过程为先进行叶片在离心力、气动力载荷下的线性静力计算。由于应力刚化的影响[σ0]→[KD],得到叶片结构更新后的刚度为[K]+[KD],再用更新后的结构刚度进行模态计算,则预应力的模态方程为:
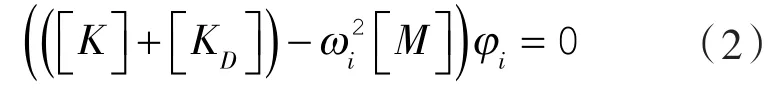
由于式(2)中含有应力刚度矩阵,说明应力刚度矩阵的准确性将对评估对旋风机叶片的振动特性产生影响,而工程上往往忽略预应力对于模态的影响,这样处理会对计算结果准确性造成误差。
将叶片的叶根位置设置固定约束,模拟轮毂位置的刚性条件,采用Block Lanczos的模态提取方法,材料采用Q235钢。计算预应力模态时对两级叶轮分别施加转速来实现离心力载荷的加载,气动力载荷为流场定常计算结果。由于结构振动中起主要作用的是低阶模态,本文模态分析仅关注前6阶固有频率[22-23]。
叶片有限元网格划分方式采用自由剖分四面体网格如图3所示。以前6阶固有频率为指标,进行网格无关性分析,由于各阶固有频率网格无关性曲线随着网格数变化呈现出相同的趋势,图4仅显示第1阶的网格无关性曲线,最终确定一级叶片单元总数为7 348个,节点总数为36 280个,二级叶片单元总数18 767个,节点86 448个。
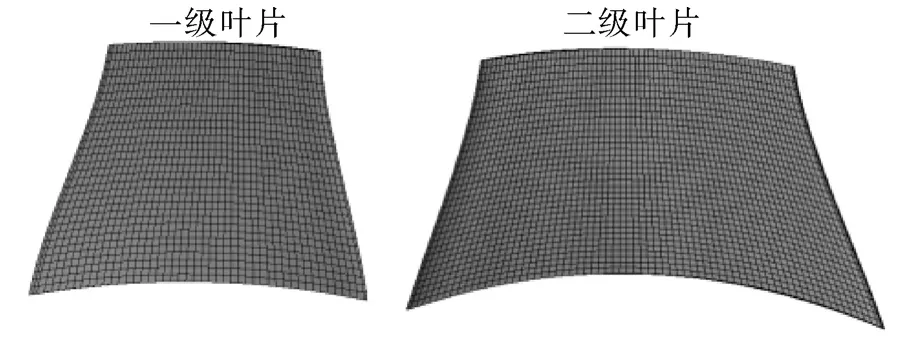
图3 叶片结构网格模型Fig.3 Grid model of blade structure

图4 结构网格无关性验证Fig.4 Grid independence verification of structure
1.3 基于模态的强迫振动响应设置
对旋风机叶片动力学分析的控制方程为:
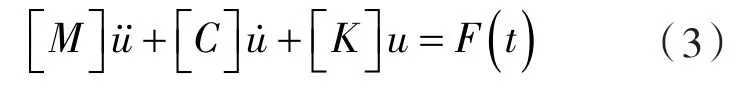
式中,,u——叶片表面节点的加速度、速度和位移矢量;
[C]——结构阻尼矩阵;
F(t)——叶片表面非定常流体激振力。
将式(3)转换为模态坐标系下的动力学方程为:
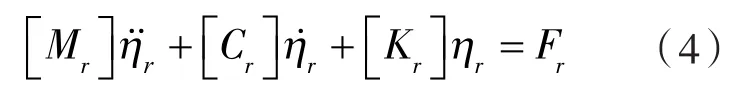
式中 [Mr]——模态质量矩阵,[Mr]=φiT[M]φi;
[Cr]——模态阻尼矩阵,[Cr]=φiT[C]φi;
[Kr]——模态刚度矩阵,[Kr]=φiT[K]φi;
[Fr]——模态力,[Fr]=φiT[F(t)];
ηr——模态参与因子。
求解该方程可得到叶片表面振动加速度。具体步骤如下:(1)三维非定常流场计算结果收敛后,将对旋风机叶片表面节点的静压保存,总时间为叶片转过一圈所需的时间;(2)进行傅里叶分析,得到对旋风机叶片表面各网格离散点的各阶激振力幅值和相位信息;(3)采用模态叠加法将非定常激振载荷的幅值和相位插值到对应叶片结构有限元网格上,实现叶片强迫振动响应的非定常气动载荷加载。
2 对旋风机非定常激振力频率分析
2.1 监控点设置
由于叶顶间隙监控点可反映出流体压力脉动特性,为了获得流动方向流体压力脉动特征,因此提取6个叶顶间隙监控点进行分析。监测点位置如图7所示,T1~T3分别位于一级叶轮叶顶前缘、中部、尾缘,T4~T6分别位于二级叶轮叶顶前缘、中部、尾缘。限于篇幅,流道其它监控点的结果未列出。
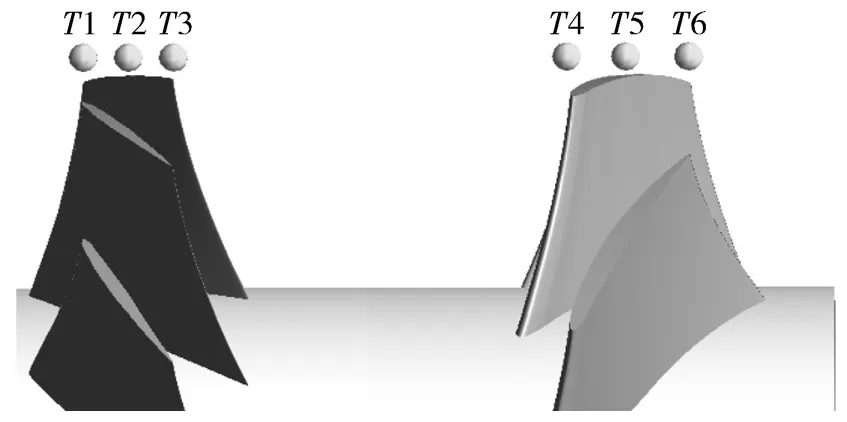
图7 压力脉动监测点位置Fig.7 Position of pressure pulsation monitoring point
2.2 激振力频率特征
非定常气动激励的主要形式为使叶片产生振动的压力载荷,可以使用压力脉动来反映流场激振力特征频率[24-27]。本文监测对旋风机流道内各点的静压变化,并通过PSD功率谱分析来获得气流激振力的脉动主频率。图9示出各监测点功率谱密度,从图可看,T1~T3监控点功率谱峰值位于一级叶轮通过频率(fBPF1=737.5 Hz)及其倍频附近,且T1处功率谱密度最强,T2,T3依次减弱,表现出在一级流道内沿着流动方向压力脉动强度逐渐减弱的趋势,这与文献[28]得到的结论一致。在二级流道内监控点T4,T5,T6也具有相似的规律,其功率谱峰值均位于二级叶轮通过频率(fBPF2=491.66 Hz)及其倍频附近,二级流道内的压力脉动强度同样沿着流动方向逐渐减弱。综上所述,对旋风机流场非定常激振力特征频率为两级叶轮的通过频率及其倍频,且在一、二级流道内激振力的大小均沿着流动方向逐渐减弱。

图9 监控点功率谱密度Fig.9 Power spectral density of the monitoring point
3 模态分析
叶片不施加任何预应力时的得到的模态结果,称为自由模态。叶片同时施加离心力、气动力下的模态称为预应力模态。从表1,2可以看出,各阶预应力模态频率高于自由模态频率,这是因为预应力的施加增加了叶片表面的应力,使得叶片表面刚度发生变化,从而增加了叶片的固有频率。

表1 自由模态固有频率Tab.1 Free mode natural frequencies
4 强迫振动响应分析
本文在设计流量下进行了对旋风机非定常计算,将非定常压力脉动作为流体激振力参与强迫振动响应计算。此处对比分析自由模态与预应力模态下的强迫振动响应。
4.1 振动加速度频谱图
考虑叶片前缘部位为气流来流方向,气流冲击较为严重,将两级叶片叶顶前缘部位设为监控点。监控点位置如图10所示。
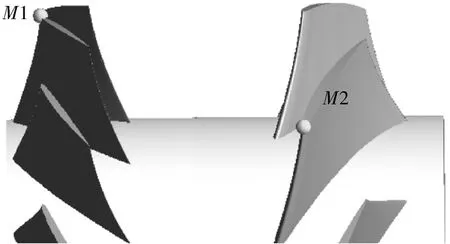
图10 叶片振动监控点Fig.10 Blade vibration monitoring point
图11,12示出了2种模态下监控点的振动加速度频谱。从图中发现2种模态下强迫振动响应峰值均出现在结构模态固有频率附近,其中采用自由模态计算结果峰值偏高,这是由于实际预应力的存在,结构表面产生内压刚化效应,增大了结构的刚度,使叶片振动幅值减弱,而自由模态未考虑这一因素的影响;3个方向中z方向的监控点振动加速度曲线高于另2个方向,这是因为z方向为气流流动方向,受到较另2个方向更多的气流冲击;两种模态计算出的一级叶片最大响应峰值频率(2 100 Hz)均出现在其叶片2阶固有频率(2 017.7 Hz)以及一级叶轮流体激振力的3倍叶频(2 212.5 Hz)附近,同时二级叶片最大响应峰值频率(2 000 Hz)与二级叶轮4倍叶频(1 966 Hz)以及叶片2阶固有频率(2 068.2 Hz)接近,这说明两级叶片监控点振动加速度响应峰值受固有频率与激振源的共同影响,当宽频流体激励力的频率接近叶片结构模态固有频率时将引起结构共振,并产生相应的振动加速度。
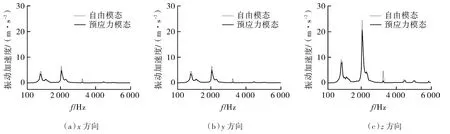
图11 监控点M1振动加速度频谱Fig.11 Vibration acceleration spectrum of monitoring point M1
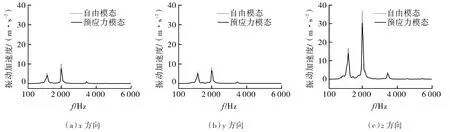
图12 监控点M2振动加速度频谱Fig.12 Vibration acceleration spectrum of monitoring point M2
4.2 监控点总振动加速度级
为了进一步衡量两种模态计算下的监控点处强迫振动响应量,本文采用总振动加速度级La来评价监控点处的振动大小,该评价指标采用对数dB形式表示,既可以适应振动强度较大的变化范围,又可以在振动幅度较小时保持精度,当La值为负时,表明其值低于规范规定的基准加速度。
计算式为:

式中arms——监控点加速度的有效值;
a0——基准加速度值,取a0=1.0×10-6m/s2。
由表2~4可知,3个方向下自由模态计算各个监控点的总振动加速度级值均高于流固耦合模态,且在x方向M1监控点处两种模态计算出的La差值最大,约1.5 dB,此时两种模态计算出强迫振动响应误差最大达到21%左右。这表明在基于模态结果进一步计算叶片强迫振动响应时,应该考虑预应力对于模态的作用,不应随意忽略。
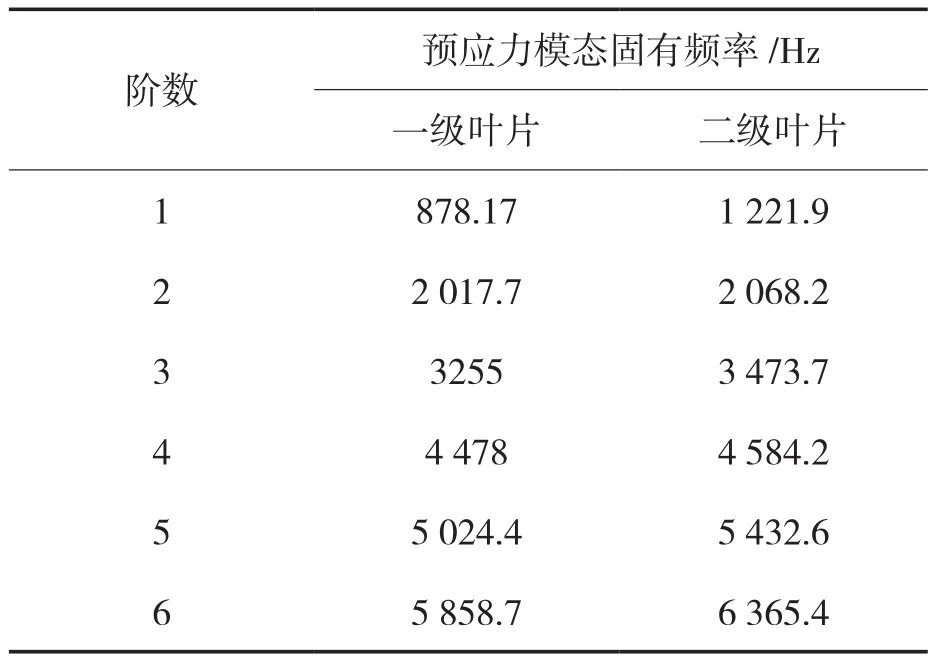
表2 预应力模态固有频率Tab.2 Prestressed mode natural frequencies

表2 x方向两种模态下监控点总振动加速度级Tab.2 Total vibration acceleration levels of the monitoring points under two modes in x direction

表3 y方向两种模态下监控点总振动加速度级Tab.3 Total vibration acceleration levels of the monitoring points under two modes in y direction
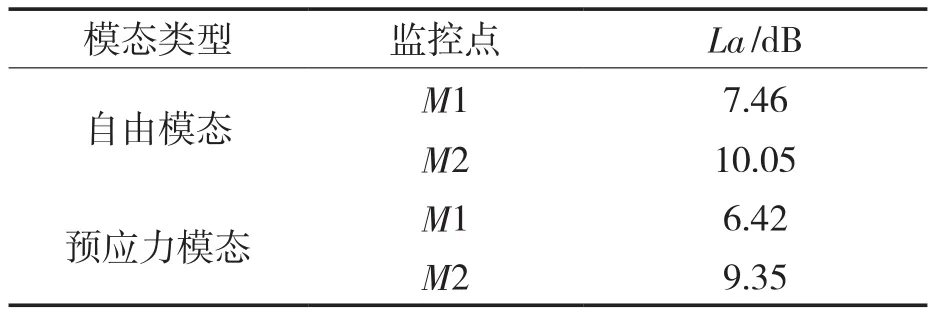
表4 z方向两种模态下监控点总振动加速度级Tab.4 Total vibration acceleration levels of the monitoring points under two modes in z direction
5 结论
(1)对旋风机流场激振力特征频率为一级、二级叶轮的通过频率及其倍频,且在一、二级流道内激振力的大小均沿着流动方向逐渐减弱;
(2)两级叶片监控点振动加速度响应峰值受固有频率与激振源的共同影响,其中一级叶片监控点加速度频谱最大峰值频率(2 100 Hz)与其叶轮的3倍叶频(2 212.5 Hz)、叶片2阶固有频率附近(2 017.7 Hz)接近,二级叶片监控点最大峰值频率(2 000 Hz)与其叶轮4倍叶频(1 966 Hz)、叶片2阶固有频率(2 068.2 Hz)接近,此时流体激振力与叶片结构发生了小幅共振,产生相应的振动加速度;(3)由于忽略了结构表面的应力刚化效应,采用自由模态计算的强迫振动响应较高估计了结构的振动幅度,这会与实际情况产生一定的误差,两种模态计算出的监控点总振动加速度级差值最大约为1.5 dB。

