好奇心驱动的深度强化学习机器人路径规划算法

张永梅， 赵家瑞， 吴爱燕

(北方工业大学信息学院， 北京 100144)

路径规划是指机器人根据对环境的感知自主选择一条从起点到终点的无碰撞路径。路径规划技术是机器人完成其他复杂任务的技术前提。常见的路径规划算法包括非智能算法(如A*、D*及其改进算法[1])以及智能算法(如蚁群算法)。

非智能算法在复杂环境中无法处理复杂高维环境信息，或者容易陷入局部最优[2]。昝新宇等[3]根据多因素综合指标改进了蚁群算法，在全局搜索能力和收敛速度上有了较大提升。此外，智能算法还包括遗传算法、强化学习算法等。其中，强化学习算法与人类学习经验试错过程最为相似。非智能算法通常将路径规划任务视为搜索问题，智能路径规划算法更加强调优化，对实时性要求不高。基于强化学习的机器人路径规划算法可不过多依赖环境，实时性强。强化学习算法通过最大智能体从环境中获得累计奖励学习到完成目标的最优策略，将强化学习用于机器人路径规划问题，近年来受到学术界和工业界的广泛关注，强化学习是目前机器人运动规划的研究热点[4-5]。

典型的强化学习算法为Q学习，该算法将奖励设为固定值或随机值，使算法收敛缓慢。当状态空间集合不再离散或离散后维数较大时，如机器人感知到多维度环境信息时，Q-learning算法将无法维护Q表。此时，需结合深度神经网络等非线性近似表示值函数或策略。使用Q学习的机器人运动规划方法无法处理高维输入[6]。

传统的强化学习方法受到动作空间和样本空间维数的限制，难以适应更接近实际的复杂问题情况，而深度学习具有较强的感知能力，能够更加适应复杂问题，但是缺乏一定的决策能力。因此，谷歌大脑将深度学习和强化学习结合，得到深度强化学习，为移动机器人复杂环境中的运动规划提供了新的思路和方向。深度强化学习具有深度学习强大的感知能力和强化学习智能的决策能力，在面对复杂环境和任务时表现突出，有助于机器人的自主学习和避障规划[7]。

Mnih等[8]于2013年提出深度Q网络(deep Q-learning，DQN)，采用Q学习的一种变种训练卷积神经网络，是深度强化学习领域的开创性工作。DQN是结合深度学习与强化学习，实现从感知到动作的端对端学习的一种全新算法。Nguyen等[9]提出改进经验回放机制的DQN机器人路径规划方法，通过计算经验数据间的相似性来决定是否存储，但该方法需更多训练次数来满足环境的探索程度。DQN依赖于在每一次最优迭代中寻找动作值函数的最大值，只能处理离散低维的动作空间。针对连续动作空间，DQN无法输出各动作的值函数。目前机器人强化学习路径规划采用离散型动作输出算法(将角速度[-2，2]区间离散为集合{-2,1,0,-1,2})的研究占大多数，离散变化的动作取值与真实场景路径规划时连续速度的情景存在较大差异。

深度确定性策略梯度(deep deterministic strategy gradient，DDPG)算法适用于连续动作空间的控制任务，DDPG解决了DQN难以对连续动作估计Q值的问题。DDPG[10]根据环境状态得到连续动作，例如给定区间内连续值。Kenzo等[11]提出基于DDPG的双足机器人导航方法，通过输入图像到卷积神经网络，端到端映射为机器人动作。Hu等[12]提出基于DDPG的空间机器人路径规划方法，引入多重约束奖励机制，使奖励更加合理。Sampedro等[13]提出基于DDPG的多翼机器人伺服控制方法，将图像状态信息映射为飞行机器人的线性速度，并运用于目标跟踪。

在基于深度强化学习的机器人运动规划方法中，训练时会出现稀疏奖励问题，在对环境的探索中，奖励在智能体学习中起着至关重要的作用，但在路径规划问题中奖励信号十分稀疏，导致智能体难以从与环境的交互中学习到最优策略，模型将因稀疏奖励问题而难以收敛。

稀疏奖励问题是深度强化学习解决实际问题面临的核心问题，在强化学习机器人路径规划方法中，智能体要在到达目标点或发生碰撞后才能获得奖励。在学习初始阶段，奖励通常依靠随机动作获取，难以获得奖励，且只有完成有利于实现任务的动作才可获得正向反馈，而这一过程在随机性的影响下较难完成。

稀疏奖励问题影响算法整体收敛效果和训练时间。稀疏奖励问题会导致强化学习算法迭代缓慢，甚至难以收敛[14]。解决稀疏奖励问题有利于提高样本的利用效率，主要研究包括经验回放机制、探索与利用和多目标学习等。其中，探索与利用根据内在奖励计算方式可以分为计数法和内在奖励法。内在奖励法通过学习环境的状态转移，利用预测误差作为内在奖励，降低环境动态的不确定性。

Bellemare等[15]提出一种将伪计数转为内在奖励的方法，通过拟合密度生成模型比较状态相似性，但在拟合模型的选择时难度较大。Stadie等[16]提出基于环境模型判断状态探索度的内在奖励方法，通过状态和动作预测新状态，但环境模型难以建立。Pathak等[17]提出基于内部好奇心模块的奖励生成方法，模型使用前后时刻状态和动作作为训练数据，以预测状态与下一时刻状态误差作为内在奖励。

现分析深度强化学习算法稀疏奖励问题产生的原因，提出好奇心驱动的深度确定性策略梯度，在行动者网络前增加好奇心模块提升奖励获取来源，在机器人运动规划训练前期奖励获取有一定提升，更充分利用状态信息。深度确定性策略梯度可处理高维数据，并且输出的是连续动作，相比深度Q网络更加平滑。

1 深度确定性策略梯度和好奇心算法

1.1 深度确定性策略梯度

深度强化学习是一种端到端的感知与控制算法，通过深度学习感知每个时刻智能体感知环境的高维度交互信息，得到具体的状态空间，按照某种策略从状态得到动作，并基于预期回报来评价各动作的价值，并将感知环境对动作的反应，不断循环该过程得到最优策略[18]，深度强化学习基本框架如图1所示。

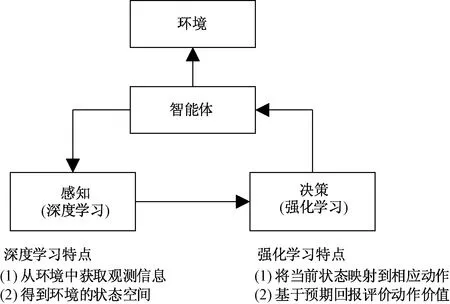
图1 深度强化学习基本框架Fig.1 Basic framework of deep reinforcement learning

因DQN只能处理离散和低维的动作空间，故对于连续控制任务无法应用。可通过离散化动作空间的方式使用，如将[0,1]动作空间离散为(0, 0.25, 0.5, 0.75, 1)，但该方式在应对大范围动作空间时会损失一定动作结构信息，而且如何界定动作数量划分标准会导致训练难度增大。

基于值函数的深度强化学习算法，如DQN，可解决离散动作空间的任务。而对于连续动作空间的任务，采用基于策略梯度的深度强化学习算法可以获得更好的决策效果。策略梯度通过不断计算策略的总奖励期望值关于策略参数的梯度来更新参数，得到最优策略。

DDPG作为一种基于策略梯度的深度强化学习算法，由Actor网络μ(s|θμ)、Critic网络Q(s,a|θQ)和Actor目标网络μ(s|θμ′)以及Critic目标网络(Target-Critic)Q(s,a|θQ′)组成，随机噪声和经验回放以离线策略的方式供网络训练[19]。

DDPG分别采用参数为θμ和θQ的深度神经网络来表示确定性策略a=πμ(s|θμ)和值函数Q(s,a|θQ)。策略网络用来更新策略，对应Actor-Critic框架的Actor。值网络用来逼近状态动作对的值函数，并提供梯度信息，对应Actor-Critic框架的Critic。在DDPG中，定义目标函数为带折扣的奖赏和，表达式为

J(θμ)=Eθμ(r1+γr2+γ2r3+…)

(1)

式(1)中：r1、r2、r3、…为第一、二、三、…时刻的奖赏；γ为奖赏折扣。

采用随机梯度下降方法来对目标函数进行端对端的优化。目标函数关于θμ的梯度等价于Q值函数关于θμ的期望梯度。

(2)

根据策略性梯度a=πμ(s|θμ)可得

(3)

通过DQN中更新值函数的方法来更新评论家网络，此时梯度信息为

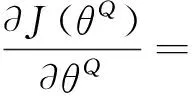
(4)

1.2 好奇心算法

强化学习作为一种依靠与环境交互试错来求解最优策略的算法，在该过程中，只有在任务成功或失败时才会得到奖励，在探索环境初期完全依靠随机性可能减慢寻找最优解速度而出现稀疏奖励问题。

好奇心驱动是一类使用内在奖励引导智能体探索环境的方法，高效探索能够更快地获得外在奖励，同时能够降低环境的奖励、状态转移的不确定性，平衡探索与利用，因此好奇心驱动可以解决稀疏奖励问题带来的稀疏性和不可靠性问题[20]。图2为内在好奇心模块(intrinsic curiosity module，ICM)结构，作为一种预测差法，包括正向模型和逆向模型。

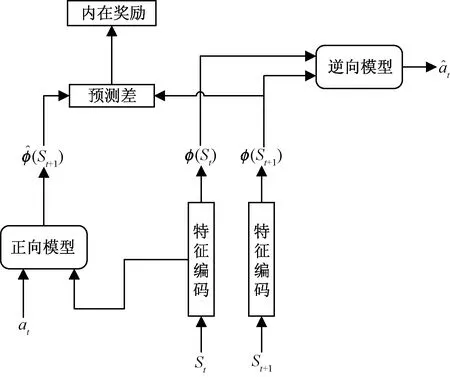
图2 好奇心模块结构Fig.2 Curiosity module structure

正向模型来预测下一步的状态为

(5)

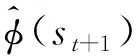
t时刻的内在好奇心奖励为实际状态表示和正向模型的误差。

(6)

式(6)中：η为控制内在好奇心奖励的比例参数，η>0。

(7)

2 改进的深度确定性策略梯度路径规划算法

2.1 加速前期训练的内在好奇心模块设计

在训练深度强化学习模型时，样本的获取过程需要耗费大量时间，特别是训练前期使用随机策略探索环境时，可能训练几百回合也无法得到第一次正向奖励。造成该问题的主要原因是稀疏奖励问题，智能体与环境交互后无法获得奖励，则该条样本对于智能体习得最优策略的贡献较小。若能缩短训练前期探索环境这一过程，即可加速学习过程，加快深度强化学习算法收敛。在实际机器人运动规划时，交互过程不仅耗时且与环境交互可能对硬件设备造成损耗，如碰撞和激光雷达寿命。

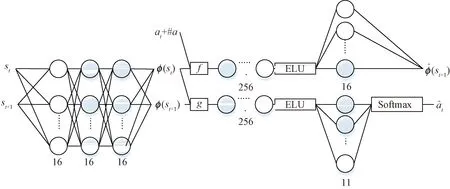
图3 内在好奇心模块具体设计Fig.3 Specific design of the intrinsic curiosity module

2.2 好奇心驱动的深度确定性策略梯度机器人路径规划算法

好奇心驱动的深度确定性策略梯度(intrinsic curiosity deep deterministic strategy gradient, ICDDPG)满足自身运动模型和环境约束条件，可在连续的动作空间中找到最优策略，通过评估到达目标点。算法的优化目标为利用当前机器人自身状态以及环境信息直接控制机器人动作(线速度、角速度)到达目标点，Actor网络与Target-Actor网络输出动作，Critic网络与Target-Critic网络负责估计动作Q值，ICM模块预测下一时刻状态给出内在奖励，经验回放池负责存储探索数据，Gazebo为仿真交互环境，奖励包括内在好奇心奖励和外部任务奖励。

如图5所示，网络训练时，通过在经验回放池中取得样本S，更新Actor网络参数以获取更高奖励。Actor目标网络根据采样的S′预估动作A′，将S′和A′传给Critic目标网络，得到下一状态的Q值，同时Critic网络计算当前状态Q值，通过最小化损失函数更新Critic网络参数。

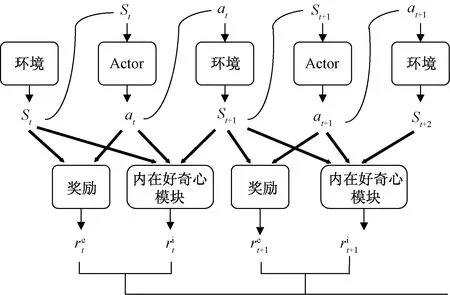
图4 加入内在奖励更新ActorFig.4 Adding intrinsic rewards to update Actor

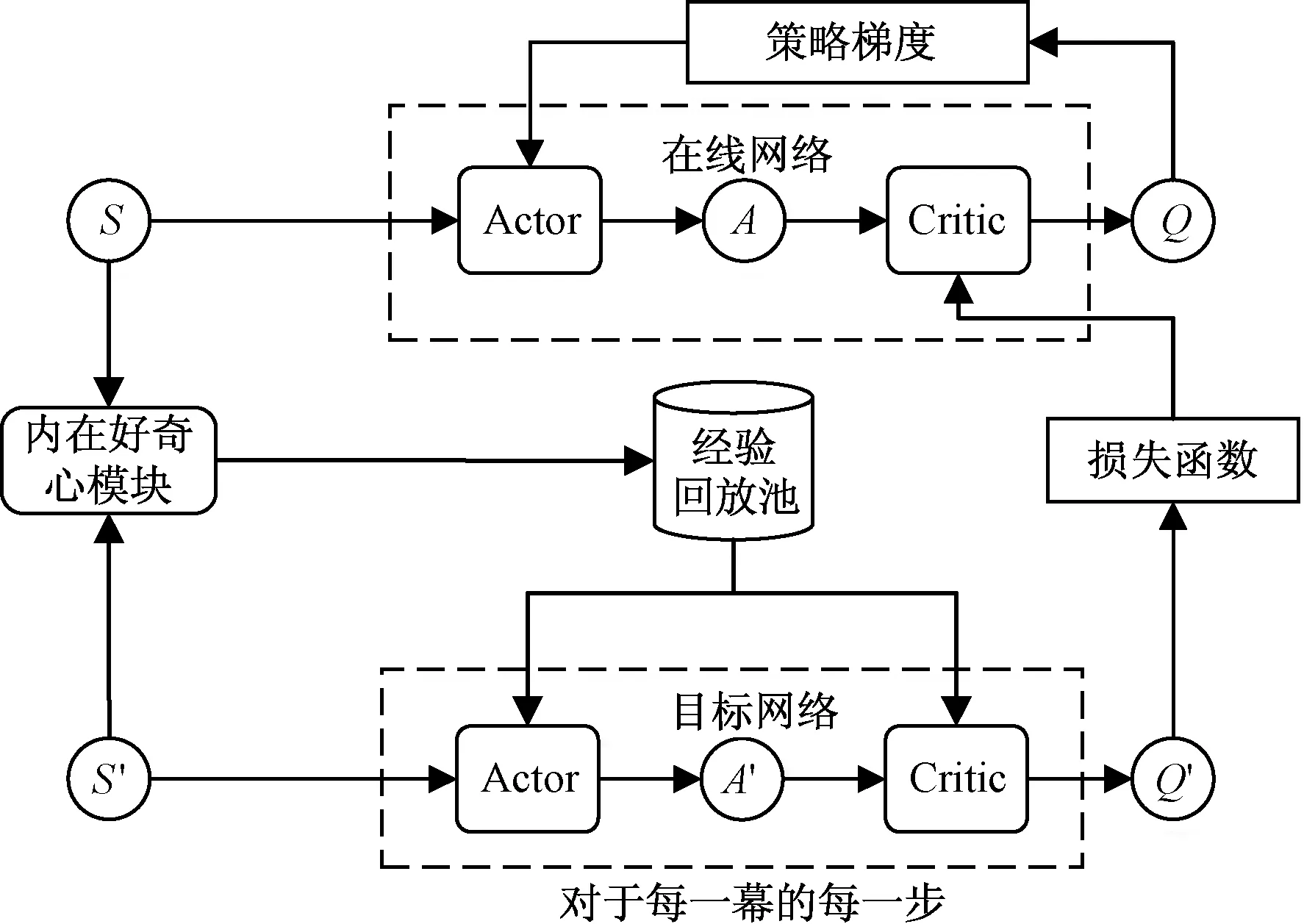
图5 好奇心驱动的深度确定性策略梯度算法流程图Fig.5 The flow chart of the curiosity-driven deep deterministic strategy gradient algorithm

3 实验结果对比与分析

按照提出ICDDPG进行移动机器人路径规划，在仿真场景内不断地学习探索，一旦机器人最大步数未碰撞、未到达目标点或发生碰撞，则复位整个场景；若到达目标点，则重新随机生成目标点，机器人将以上一个目标点作为起点进行路径规划。

Gazebo仿真场景如图6、图7和图8所示，仿真机器人为Turtlebot3-Burger，如图9所示。仿真场景1和2大小均为4.5 m×4.5 m，目标点位置从[-1.5, -0.5, 0.5, 1.5]随机生成，[1,1]、[-1,1]、[1,-1]、[-1,-1]为障碍物。仿真场景3大小为20 m×20 m，包括静态障碍物和动态障碍物，目标点位置在围墙内随机生成，设置动态障碍物在随机运动时只能与仿真机器人发生碰撞。在矢量空间中，机器人的动作主要由线速度和角速度进行控制，线速度约束为0～1 m/s，角速度约束为-0.5～0.5 rad/s，且均为连续值。仿真机器人为Turtlebot3-Burger，其自身与环境交互参数如表1所示。

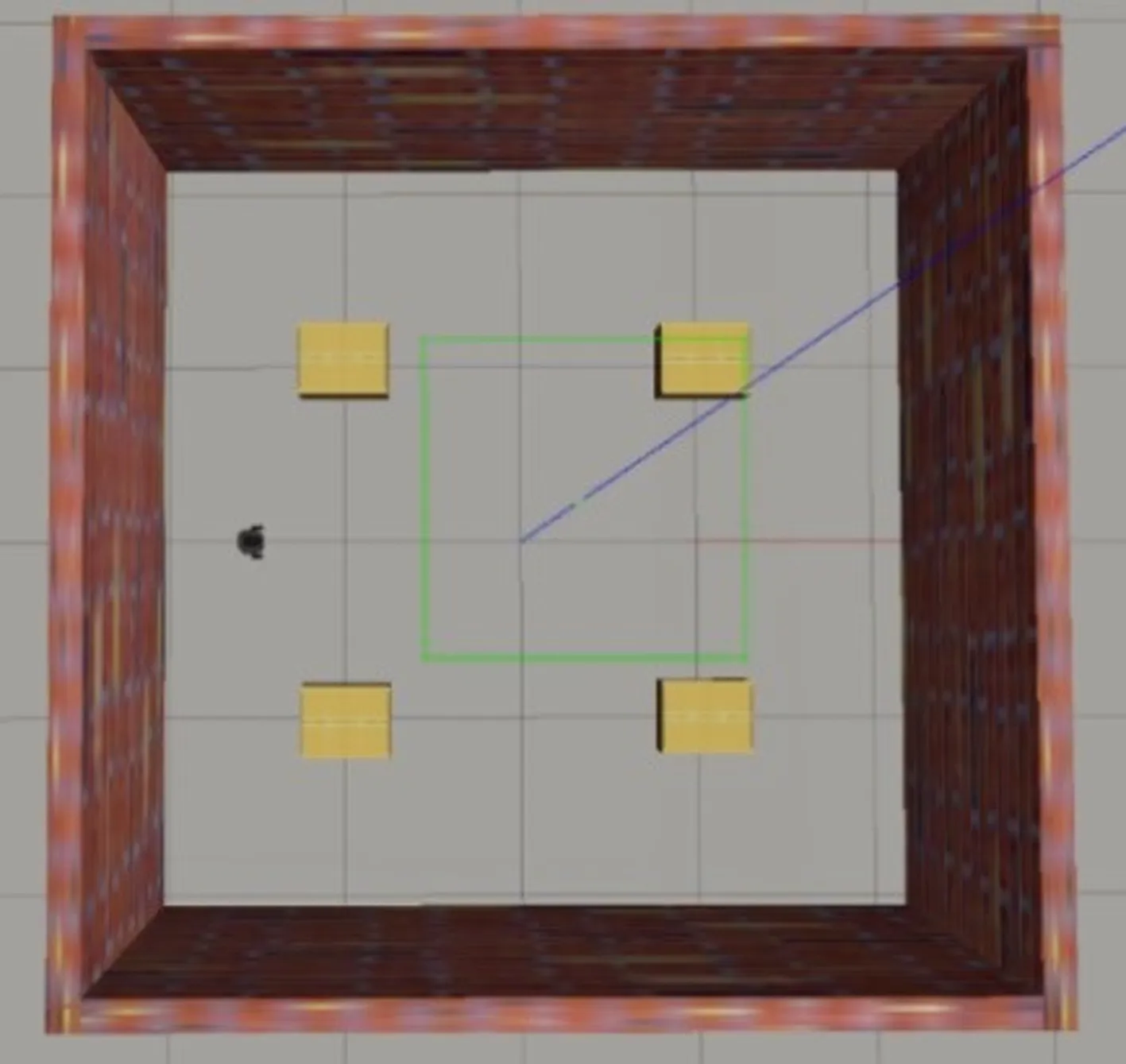
图6 Gazebo仿真场景1Fig.6 Simulation scene 1 for Gazebo

图7 Gazebo仿真场景2Fig.7 Simulation scene 2 for Gazebo

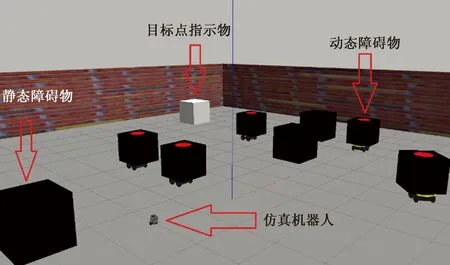
图8 仿真场景3Fig.8 Simulation scene 3 for Gazebo

图9 仿真机器人Fig.9 Simulation robot

表1 仿真机器人参数Table 1 Simulation robot parameters

DDPG选取策略为ε-greedy，训练初始阶段依靠随机性探索环境，经一定步数后，选择随机性概率以0.992衰减，根据网络生成动作概率增加。Actor与Critic网络隐藏层的激活函数均为relu，Actor输出层线速度和角速度，激活函数分别为sigmoid和tanh。网络模型的具体超参数见表2，其中网络神经元考虑了移植到真实硬件环境时，使用神经元数相对较少，因此将每批次经验条数设置为128。

机器人路径规划仿真实验共设置200个回合，经一定回合，经验回放池满足储存3 000条数据样本，开始供Actor、Critic和ICM训练并更新目标网络，并继续完成其余回合任务。机器人路径规划到达目标点奖励为150，发生碰撞为-200。奖励函数设置为

(8)

式(8)中：Dscan为激光雷达感知到的距离；Dgoal为机器人到达目标点的最小距离；Dmin为机器人与墙壁或障碍物的最小碰撞距离；α、β为机器人在最大步数未碰撞而结束回合时的奖励因子，为了平衡任务回合奖惩，将其设置为0.1和0.2；Dir和Dis分别为回合结束时机器人与目标点朝向角差值和距离。

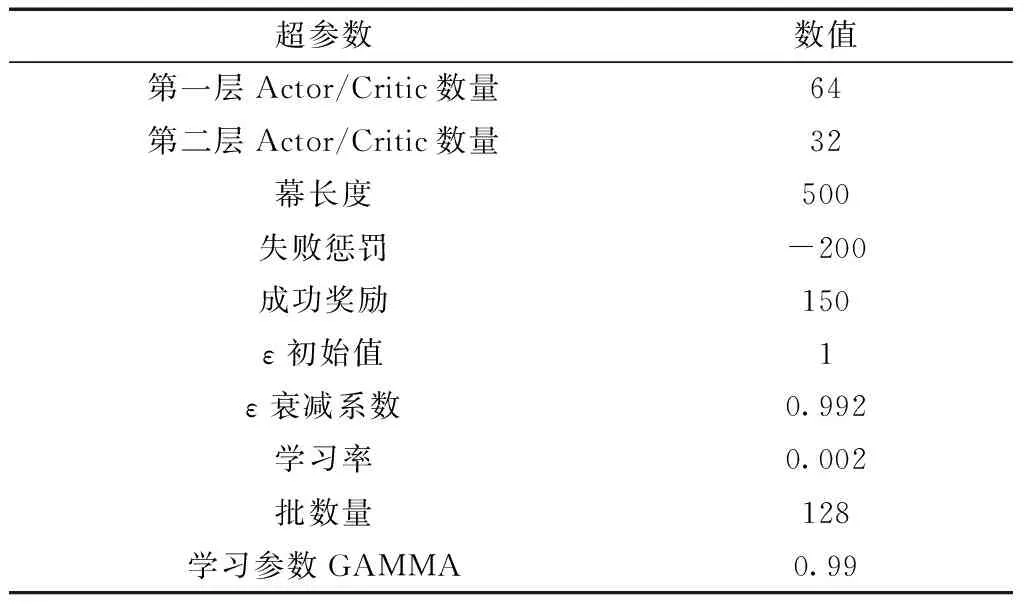
表2 超参数Table 2 Hyper-parameters

通过表3可得出，训练前期因采用ε-greedy策略，处于探索环境阶段时随机性较大，DQN算法每回合所获得的奖励几乎全部为负值，在只有少量样本的情景下难以收敛，DDPG算法和ICDDPG算法的平均奖励呈上升趋势，而ICDDPG算法所得奖励明显高于DDPG算法，表明内在好奇心模块可在一定程度上加速奖励的获取。

在以上200个回合的仿真实验中，如图10、图11所示。DQN、DDPG和提出的ICDDPG在仿真场景1中的平均奖励分别为-188.2、-18.2和4.2，在仿真场景2中的平均奖励为-184.8、-15.8和2.2。在200个回合训练中，ICDDPG算法在两个仿真环境中目标点到达次数分别为33次和36次，DDPG为10次和18次，DQN为16次和20次。

ICDDPG算法可以通过感知的状态信息获得额外奖励，有利于前期随机性较高时的训练。随着训练回合的深入，随机性降低，而动作通过算法得到的概率增加，机器人进入利用知识阶段，到达目标点次数增加，每次训练获得的奖励值不断增加，即机器人能够较好地利用学到的知识到达目标点。

如图10、图11所示，仿真场景3的实验结果表明加入ICM后，训练前期奖励获取有一定提升，ICDDPG相比于DQN所得奖励有明显提升，与DDPG相比大多数回合的奖励更高，DQN、DDPG和ICDDPG的目标点到达次数分别为2、13和19次。本文算法能够更充分利用状态信息，好奇心模块能够加速前期训练，使得算法能更快收敛。

在训练更多回合算法所得奖励稳定时，使用该模型在实际场景下进行了无障碍、静态和动态障碍实验，图12为机器人硬件平台ARTrobot在真实环境中情景。

表3 每40回合平均奖励Table 3 Average rewards for every 40 rounds

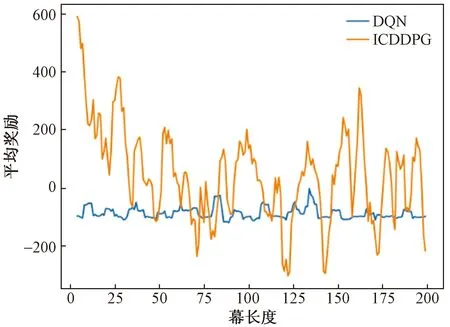
图10 在仿真场景3中DQN和ICDDPG平均奖励对比图Fig.10 Mean reward comparison chart of DQN and ICDDPG in simulation scene 3

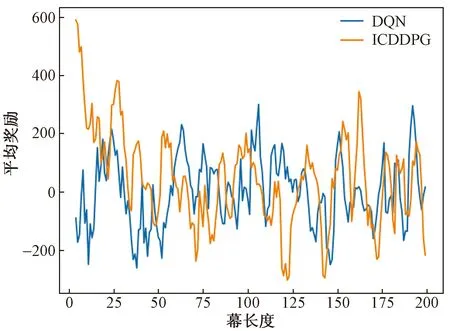
图11 在仿真场景3中DDPG和ICDDPG平均奖励对比图Fig.11 Mean reward comparison chart of DDPG and ICDDPG in simulation scene 3

图12 ARTrobot 机器人Fig.12 ARTrobot robot

在图13的无障碍场景下进行实验时，由于在训练前期使用ε-greedy策略，给定的是随机动作，并受到墙壁影响是非直线，但最终成功到达目标点。

在图14的静态障碍地图中，目标点为障碍后方，机器人与目标点间连线有一个静态障碍，机器人在与障碍的距离大于碰撞距离时，按照直线进行运动规划，小于碰撞距离时，机器人受到碰撞影响较大，进行避障，并到达目标点。

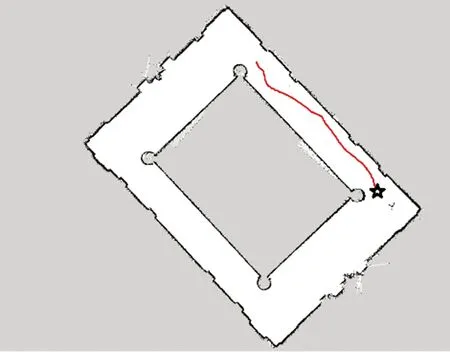
图13 无障碍路径规划Fig.13 Accessible path planning

图14 静态障碍路径规划Fig.14 Static obstacle path planning

在图15以人为动态障碍，以柱子为静态障碍的场景中。当机器人靠近时，刻意去往机器人路径规划的方向，由于机器人根据激光雷达发布动作，成功进行避让，并继续靠近目标点，在给机器人留有可达路线的余地后，可成功到达。对于本文算法的真实环境实验，在以上目标设置中，在某些情况下可以达到近似最佳路径。

图15 动态障碍路径规划Fig.15 Dynamic obstacle path planning

4 结论

分析了深度强化学习算法稀疏奖励问题产生的原因，提出了一种基于好奇心驱动的深度确定性策略梯度路径规划算法，将激光雷达、目标点距离及自身位置信息作为状态样本，以连续的线速度与角速度作为动作输出，加入内在好奇心模块提升奖励获取来源，提高感知信息的利用率。基于深度确定性策略梯度算法在Gazebo中设计了仿真实验训练，验证了内在好奇心模块有利于解决深度强化学习算法训练初期随机性高而奖励较难获取的问题。在实际场景中进行了实验，验证了本文算法的有效性。