基于MATLAB 的粗细联输送系统控制策略研究

杜博文 黄克华,2 张立杰 周红雷 张纯宇

（1.新疆大学，新疆乌鲁木齐，830046；2.新疆利华纺织有限公司，新疆阿克苏，843013）

清梳联、粗细联、细落联以及络筒与自动成包系统是连接纺纱各工序、实现智能化升级的关键。纺纱车间安装粗细联后，可实现粗纱、细纱制造流程的自动化和连续化，使生产效率和产品质量大幅提高，进一步提升了纺纱企业制造智能化水平。纺织企业中，粗纱和细纱工序之间粗纱运输、贮存和领用是一项复杂的系统。一旦生产调度或操作出现错误，轻则导致半制品以及成品的生产供应不平衡，影响细纱生产效率，重则会造成纱线错号［1］。

1 控制策略与方案设计

本研究中粗细联输送系统的目的是使粗纱在输送导轨上能够选择合适的速度。粗细联输送系统选择主从电机控制方式，对粗纱运输、贮存和领用的速度进行控制。其中，粗纱运输机构中的电机为主电机，贮存机构和领用机构中的电机为从电机。在控制系统中，主电机和从电机的速度由变频器控制，而变频器的控制模式为U/F控制模式［3］。利用安装在主电机和从电机上的旋转编码器采集速度反馈信息，比较主电机和从电机的转速差。然后设计具有补偿原理结构的模糊PID 控制器，将对比后的速度差再经模糊PID 控制器模糊运算后提供控制器输入端，构成了速度控制闭环，从而改善了主从同步控制系统的动态反馈、稳定性和抗干扰特性。

2 输送系统传递函数的建立

2.1 电机传递函数

一个表示线型输入和输出关系的函数表达式叫传递函数。传递函数能充分解释系统参数变化后对输出的具体影响，传递函数也可以确定为系统的输出响应。本研究选取3 台同型号同参数的三相异步电机，其电机传动函数变量（或参数）包括同步转速nd（r/min）、额定频率f（Hz）、额定功率PN（kW）、转差率s（%）、额定转速n（r/min）、额定转矩T（N·m）、电机相数M（相）、电机极对数P（极）、额定电压U（V）、转子绕组电阻R（Ω）、电机转子转动惯量J（N·m·s²）、转子质量G（kg）、转子直径D（m）和重力加速度g（m/s2）等，以此确立三相电机变频调速系统的增益系数函数Kr。因为主从三相转子电机为同型号同参数，故主从电机控制传递函数G(s)的表示如式（1）所示。

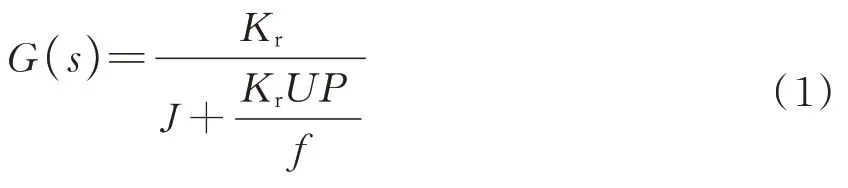
2.2 变频器控制方式

矢量控制是变频器最常见的控制方式，其基本原理是基于电磁定向原理，利用检测并调整驱动电机定子的电流损耗，来调整电机的励磁电流和转矩电流，进而实现对驱动电机转速的调整［4］。与其他变频器方法比较，矢量控制引入了频率补偿功能，减少了转速调整偏差，也减少了对低速时定子电压的影响，从而增强了对电气动作响应的准确度和稳定性。变频器传递函数G1（s）的表示如式（2）所示。

式中：Ts为平均控制滞后时间（s）；K为比例系数。

3 传统PID 控制算法

3.1 PID 控制原理

作为一种线性控制器，PID 控制器本身是一种基于信息估计的简单控制算法。其控制偏差e(t)可根据给定值r(t)与实际输出值y(t)构成。PID 控制是将偏差按比例、积分和微分通过线性组合构成控制量，对被控制对象进行调节控制，其控制方式如式（3）所示。

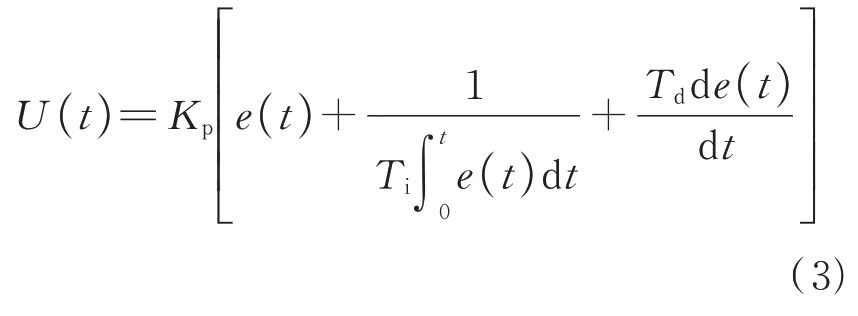
式中：U(t)为控制器输出值；Kp为比例调节系数；e(t)为偏差值；Ti为积分时间系数；Td为微分时间系数；Ki为积分系数；Kd为微分系数；Ti=

将上式改写成传递函数形式，如式（4）所示。

在控制电路运行过程中，为了达到实际控制条件，并寻求最优化的控制参数，就必须对控制器中3 个参数加以设定。Kp比例调节是通过增加比例系数，减小系统控制的调节误差，提高系统的反应速率。Ki积分调节主要为了减少系统静态误差，进一步提高控制器工作运行稳定性，同时增强控制器的无差度和抗干扰能力。Kd微分调节能够反映系统偏差信号变换速度，当调节系统中存在较大差值时，可以提前引入修正量，从而提高系统动态调整性能。

3.2 PID 控制器设计仿真

在MATLAB 软件系统中，构建粗细联输送系统速度传统PID 控制器仿真模型，通过仿真可得传统PID 控制的系统阶跃响应曲线［5］如图1 所示，其系统误差曲线如图2 所示。

2.2.3 两季稻合计产量比较 对照黄华占产量为12 736.44 kg／hm2，居第七位，比对照增产的品种有 6个，产量由高到低依次是天两优953、黄广油占、甬优4949、两优33、黄科香1号、黄科香2号，其中天两优 953 产量最高，为 14 481.09 kg／hm2，比对照增产 13.70%；A 优 338产量最低，比对照减产 9.02%。

从图1 和图2 中不难看出，即使通过长期调试的传统PID 控制器，仍没有取得非常满意的曲线，还存在着控制系统的响应曲线超调以及稳定后仍出现正常波动的状况，且调整时间也相对较长，同步控制效率并不好［6］。

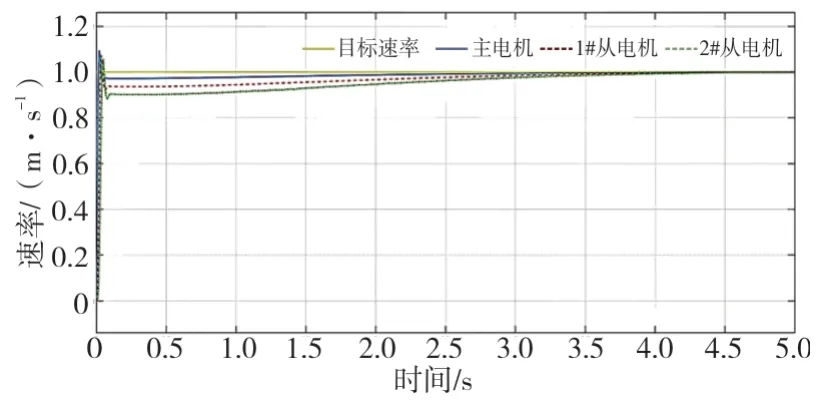
图1 传统PID 控制系统阶跃响应曲线

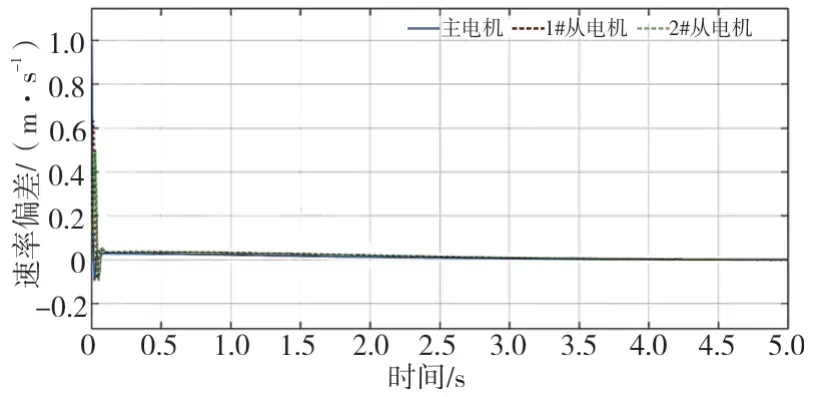
图2 传统PID 控制系统误差曲线

4 模糊PID 控制算法

4.1 模糊PID 控制原理

与传统PID 控制系统相比，模糊PID 控制系统是目前较为领先的一类控制器，能够测量并解析控制器过程中的不确定条件、参量、延时、扰动因素，并采用模糊推理的方式实现PID 参数kp、ki、kd的实时自动调节，既保留了传统PID 系统设计原理简洁、应用简便、鲁棒性强等优良特性，也增加了灵敏度、适应性和操控精确度等特性。

模糊控制原理如图3 所示。其模糊控制属于二维逻辑控制器。整个系统内部参数的模糊处理、模糊规律的运算、对模糊决策的判断和PID 控制是通过模糊PID 控制器的方式控制整个流程。模糊控制规则由中央控制台计算并实施，首先由控制器读取传感器反馈的发电机转速数值，将转速数值和指定数值加以对比从而得到误差数值［7］。

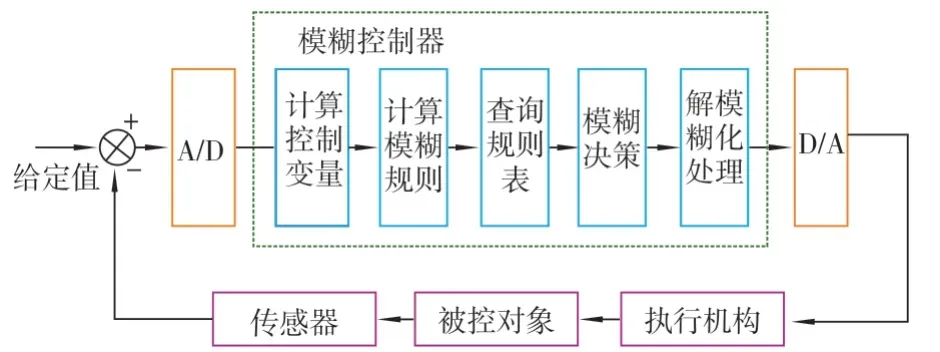
图3 模糊控制原理图

在模糊控制器对误差数据进行模糊化处理过程中，对误差数据进行处理后将获得模糊输出量U=E×R。其中，E为模糊矢量子集；R为模糊控制规则。

模糊PID 控制通过偏差e和偏差变化率ec作为控制器的输入量，模糊量E和ec都是经过对模糊规则模糊推理，并查阅由模糊规则表设定的PID 控制器参数，经过运算模糊决策加以调节，再经过模糊推理获得模糊控制量U，最后经过解模糊化获得控制量u并发送给控制对象输出［8］。

以传统PID 为基准，模糊PID 控制器的设计思路如图4 所示。

图4 模糊PID 控制器

经过调整之后放入的PID 参数是模糊控制的输出，而速率偏差变化率ec和速率偏差e是模糊控制的输入，如式（5）～式（7）所示。

基于以往对PID 控制参数调整的成功经验，在模糊控制设计架构中，由速率偏差e与速率偏差变化率ec的大小和正负确定了PID 基本参数的波动。将其定义在NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）这7 种模糊集合中，并按照表1～表3 中的规则加以选取。

如表1 所示，当速率偏差e与速率偏差变化率ec的值均是负大时，说明现在存在很大的速率偏差，并且速率偏差e在短时间内变化得很快，系统稳定性下降。要使速率得到迅速恢复，系统的稳定性得到提高，只能用很大的比例进行快速调节。将上述规律整理成规则：e=NB 且ec=NB时，Δkp=PB。

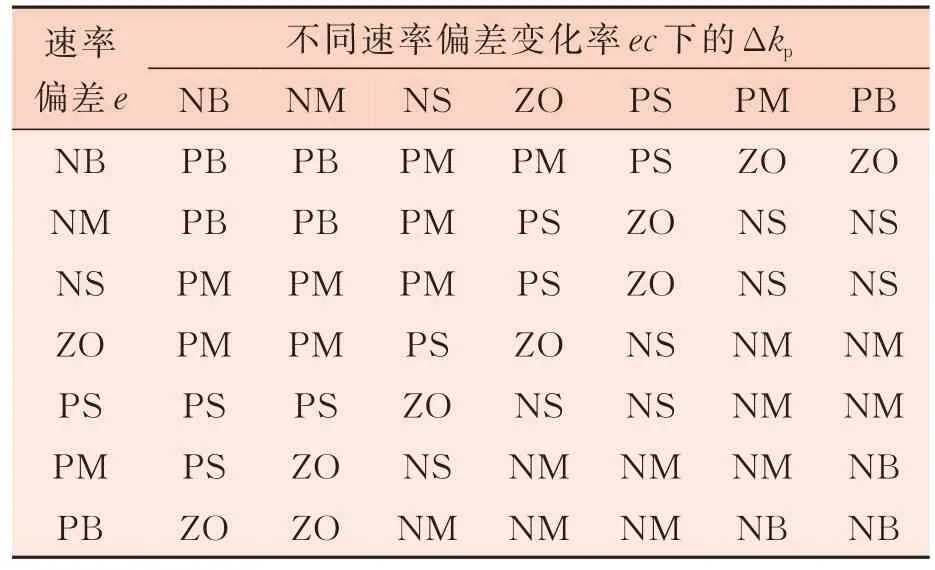
表1 比例系数增量Δkp的模糊规则

如表2 所示，当速率偏差e与速度偏差变化率ec的值均是正大时，说明现在存在很大的速率偏差，并且速率偏差e在短时间内变化得很快，系统稳定性下降。要使速率得到迅速恢复，系统的稳定性得到提高，只能用很大的积分进行快速调节。将上述规律整理成规则：e=PB 且ec=PB时，Δki=PB。

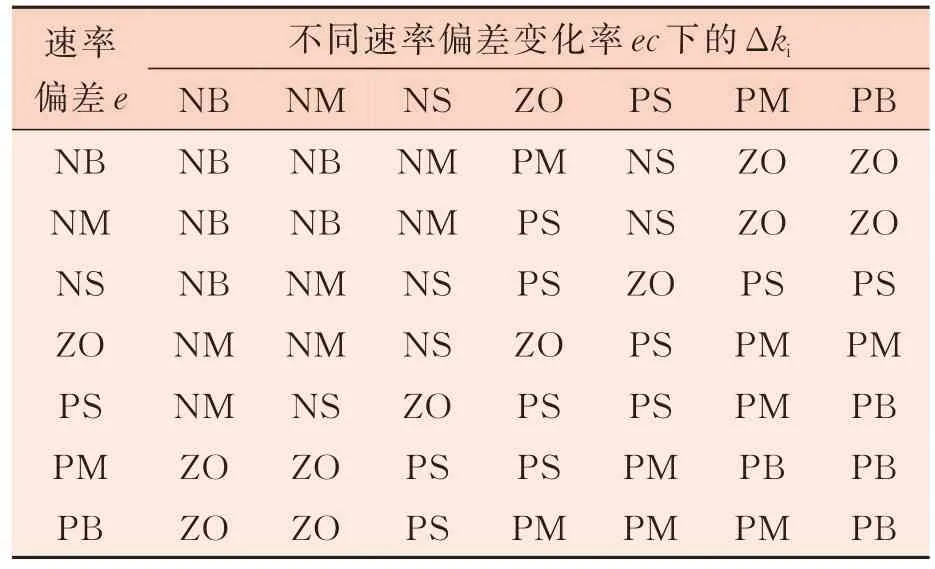
表2 积分系数增量Δki的模糊规则

如表3 所示，当速率偏差e的值为负中、速率偏差变化率ec的值为正中时，说明存在较小的速率偏差，并且输送速率并没有产生很大的超调量。当速率偏差e的值为正中、速率偏差变化率ec的值为负中时，说明存在较小的速率偏差，并且输送速率并没有产生很大的超调量。将上述规律整理成规则：e=NM 且ec=PM 时，Δkd=NS；e=PM 且ec=NM 时，Δkd=NS［9］。

4.2 模糊PID 控制器设计仿真

使用Matlab Fuzzy Toolbox 建立一个二输入三输出的模糊规则控制器并编辑模糊规则以及隶属函数e、ec、kp、ki、kd。粗细联输送系统的主从电机转速控制仿真模型已在MATLAB 软件的Simulink 工具箱中所建立。对模糊PID 控制系统模块进行系统仿真模拟计算，并得出了模糊PID控制电机模型的系统阶跃曲线和系统误差曲线，如图5 和图6 所示。

图5 模糊PID 控制系统阶跃响应曲线

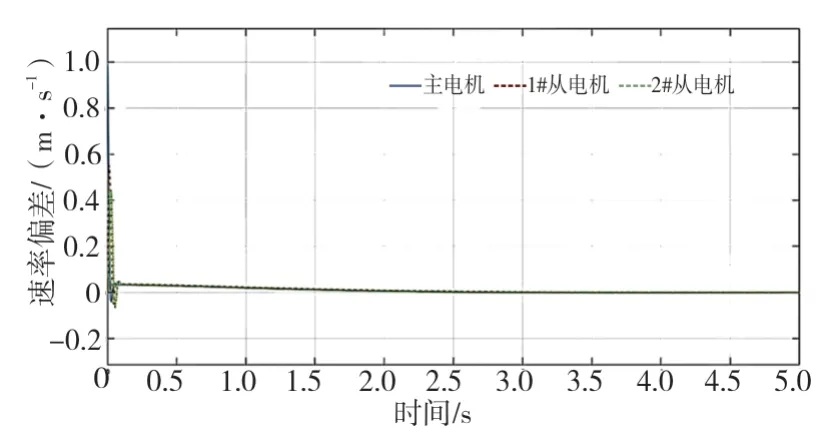
图6 模糊PID 控制系统误差曲线

由图1 与图5 可以看出，传统PID 控制系统阶跃响应曲线在4 s 以后趋于平稳，模糊PID 控制系统阶跃响应曲线在2.5 s 后趋于平稳，图1 曲线的峰值数值比图5 曲线峰值数值大，而传统PID 控制系统超调量为17%，模糊PID 控制系统超调量为5%。采用模糊PID 控制算法调节时间减小，系统的响应速度加快，控制系统的振动和超调得到有效减小。

由图2 与图6 可以看出，传统PID 控制系统误差曲线在3 s 后趋于平稳，模糊PID 控制系统误差曲线在2 s 后趋于平稳，而图2 曲线的峰值数值绝对值比图6 曲线峰值数值绝对值大，可发现与传统PID 控制系统相比，模糊PID 控制系统调整偏差时间也明显降低。这就大大增加了系统在扰动期间的稳定性［10］。

5 结语

本研究建立了变频器和电机之间的速度传递函数，并选用了传统PID 控制和模糊PID 控制用于粗细联输送系统速度的调节算法。根据两个速度控制算法在MATLAB 中构建了拖链速度控制的仿真模型，并设计了模糊PID 控制器规则的检索表。通过对传统PID 控制与模糊PID 控制仿真结果的对比可以看出，传统PID 控制在对输送速度调整的控制精度以及在对控制系统误差上的调整效果均不如模糊PID 控制好。模糊PID 控制能更有效抑制输送执行速率调整时产生的振荡和超调，从而减少输出机构转速的波动，并改善输送系统的运行稳定性。因此，选定模糊PID 控制用作粗细联输送系统的运行速度调节算法控制效果较为理想。