基于数学核心素养下深度教学的三种策略——以事件的关系与运算为例

周 瑛

(浙江省永嘉中学，浙江 永嘉 325100)

“事件的关系与运算”这节课的课程标准要求：了解随机事件的关系与运算，结合实际问题，知道随机事件的含义，并能识别它们之间的关系；知道随机事件的关系与运算的集合表示，能用简单随机事件表示复杂的随机事件，能结合实例进行随机事件的并交运算

概率研究的一个重要方法是建立一些运算法则，用简单事件的概率推算复杂事件的概率这就需要研究事件之间的关系与运算，而用简单事件的运算表示复杂事件的概率是概率学习的一个难点所以，教师要通过不同语言转换及多种不同方法突破此难点,为学生后续学习事件独立性、概率的基本性质、概率的计算、排列组合、随机变量分布列等内容打下坚实的基础

基于以上分析，下面谈谈如何进行基于核心素养下的深度教学策略

一、加强教师对数学学科素养内涵的深刻理解

事件的关系与运算的教学目标是培养学生数学抽象、逻辑推理、数学建模、数据分析、数学运算的核心素养和数学思想方法,重点是培养学生的数学抽象、逻辑推理的核心素养

(一)数学抽象

特征：(1)符号式：数学概念、学习方法都可以进行抽象，都可以使用抽象的符号来表达

(2)阶梯式：逐级抽象，下一次的抽象是建立在一次抽象材料的基础之上，甚至在更早的抽象材料上拾级而上

(3)广泛性：高度的抽象必然有高度的概括

如，本节课至少有四次抽象，具体如下：

第一次抽象：

引入问题：在掷骰子的试验中，观察骰子朝上面的点数，可以定义许多事件

设计意图：要求学生将自然语言转化为符号语言，再转化为图形语言

事件集合形式事件集合形式C1=“点数为1”C1={1}C2=“点数为2”C2={2}D1=“点数不大于3”D1={1,2,3}D2=“点数大于3”D2={4,5,6}E1=“点数为1或2”E1={1,2}E2=“点数为2或3”E2={2,3}F1=“点数为偶数”F1={2,4,6}F2=“点数为奇数”F2={1,3,5}

第二次抽象：

将事件的关系与运算用自然语言、符号语言、图形语言三种语言描述

事件的关系或运算自然语言符号语言图形语言包含关系A发生则B一定发生B⊇A(或A⊆B)相等关系A发生B一定发生,且B发生A一定发生B⊇A且A⊇B(或A=B)并(和)事件A与B至少有一个发生A∪B(或A+B)交(积)事件A与B同时发生A∩B(或AB)互斥事件A与B不能同时发生A∩B=∅对立事件A与B有且仅有一个发生A∩B=∅A∪B=Ω

第三次抽象：

模型抽象：

(1)较复杂的试验，按模型归类可轻而易举得以解决例如,抛掷一枚硬币；1个产品是正品还是次品；射击是否命中；新生儿的性别等这些试验的样本空间具有相同的结构这一模型的学习可为两点分布打下基础

(2)抛掷3枚硬币；抛掷3次骰子；观察三个元件构成的电路是否通畅等都是3次重复试验的问题依次类推，可以得出次重复试验模型,放球入盒、两人比赛问题也可以化为有放回摸球问题这一模型的学习可为二项分布打下基础

(3)抽签问题：抽到次品与正品；摸球不放回等都可以化为不放回模型，为超几何分布的学习打下基础

(4)两个随机事件运算结果抽象

第四次抽象:

方法抽象：如类比、归纳等研究方法

(二)逻辑推理

逻辑推理是指从已有事实和命题出发，依据规律推出其他命题的思维过程主要包括两类，一类是从特殊到一般的推理，推理形式主要有归纳、类比；另一类是从一般到特殊的推理，推理形式主要是演绎

从数学学习的研究过程来看，我们经常使用如下的逻辑思考方法：

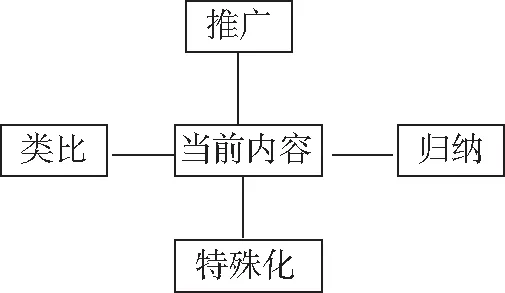
它突出了联系的特点，通过类比、推广、特殊化等方式，可以有力地促进学生的数学思考，使学生更有效地寻找自己感兴趣的问题，从而获得研究方法的启示

本节课可以用集合的观点来研究事件的关系和运算：

此外，事件关系与运算的得出都是从实际问题出发，先举实例，由特殊到一般，再从一般到特殊同时，教师选的例子也应呈现进阶性，事件个数从一个到二个，再到三个，再到个

数学思维活动是数学素养形成与发展的核心过程要素，有效的问题链可以引领学生进入深度学习基于问题链的概念课堂教学应着眼于学生的最近发展区，在学生原有的基础上进行，通过独立活动提升其解决问题的水平，再提供需要挖掘、有难度的内容激发学生的潜能，提升学生的发展水平，并超越其最近发展区而达到下一发展阶段，教师在此基础之上进行下一个阶段的教学

设计问题链的流程：

本节课可以设置以下问题链：

问题1：你能说说本试验的其他事件吗？试用集合的形式表示这些事件

问题2：借助集合之间的关系与运算，你能发现这些事件之间类似的联系吗？

问题3：你能说出实际生活中具有包含关系的随机事件吗？

问题4：你能归纳概括一下不可能事件的定义吗？

问题5：你能举出事件的一个互斥事件吗？对立事件呢？

问题6：互斥事件与对立事件的联系和区别有哪些？

问题7：三个事件的并事件；交事件你能写出来吗？

问题8：你能写出表示两个元件工作状态的样本空间吗？

问题9：你能用集合的形式表示事件、事件以及它们的对立事件吗？

问题11：如何用事件的运算得到新的事件

问题12：将串联改为并联，你又如何看待这几个问题？2个元件改为4个元件，你又如何解决这几个问题？摸球事件与电路试验有何联系？

问题13：你有什么收获？

三、提升学生的参与度

学习主体在思维活动中的经历、体验、反思过程中产生的情感共鸣是其数学素养形成与发展的催化剂

深度学习流程图如下：

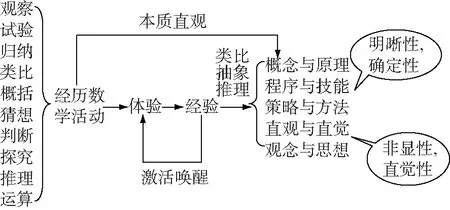
具体措施：

1适当留白

2设置学生感兴趣的探究题

如：以通用技术中接线路问题为切入点,层层递进设置问题,提升学生的学习兴趣

现有4个外观一致的电子元件甲、乙、丙、丁，每个元件可能正常或失效

如图，由甲、乙两个元件组成一个串联电路，观察两个元件正常或失效的情况设事件=“甲元件正常”，=“乙元件正常”

(1)写出表示两个元件工作状态的样本空间

(2)用集合的形式表示事件，以及它们的对立事件

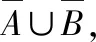
设计意图：让学生进一步巩固概念

2已知电子元件甲、乙(标号为1和2)正常，丙、丁(标号为3和4)失效，现从中不放回地依次随机抽取2个元件，如图，组装成一个串联电路

设事件=“第一次抽取到正常元件”，=“第二次到抽取正常元件”，

=“两次都抽取到正常元件”，=“两次都抽取到失效元件”，

=“两次抽取的元件状态相同”，=“电路不能正常工作”

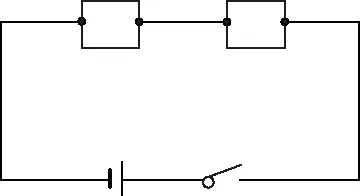
(1)用集合的形式分别写出试验的样本空间以及上述各事件

(2)事件与，与，与之间分别有什么关系？

(3)∪与事件有什么关系？∩与事件有什么关系？

变式方法:

(1)将电子元件甲、乙、丙、丁改为红球1号、2号，绿球3号、4号

(2)从中不放回地依次随机抽取2个元件改为从袋中不放回地依次随机摸出2个球

(3)=“第一次抽取到正常元件”→“第一次摸到红球”，

=“第二次抽取到正常元件”→“第二次摸到红球”，

=“两次都抽取到正常元件”→“两次都摸到红球”，

=“两次都抽取到失效元件”→“两次都摸到绿球”，

=“两次抽取的元件状态相同”→“两个球颜色相同”，

=“电路不能正常工作”→“两个球颜色不同”

上述例题从两个元件的串联，到两个元件的并联，再到四个元件选两个进行串联，再到抽象出一样模型的摸球问题，逐层递进问题还可以挖掘，如拓展为三个正常元件等，让学生带着问题回顾课堂所谓学习不止，探究不息

3给学生展示的机会与适当的鼓励

教师要经常巡视班级，多多倾听学生的想法，给予学生正面的评价与鼓励，让学生充满学习数学的成就感，对数学的学习更加有兴趣，同时设置浅层的问题，帮助学困生逐渐提起学习数学的兴趣，使其在不断的鼓励中形成数学思维

四、结 语

数学的世界是星辰大海，是浩瀚宇宙，它深邃唯美作为教师，应该带领求知欲旺盛的学生们探究数学，感悟数学，享受数学纸上得来终觉浅,绝知此事要躬行,教师在平常教学中要践行基于数学核心素养下深度教学的三种策略,真正提升学生的数学思维，从而实现立德树人