叉车转向桥有限元软件的开发与应用分析

王彬 马成云

合肥和安机械制造有限公司 安徽 合肥 231200

1 有限元计算要点

使用常规ANSYS、ABAQU软件对转向桥进行仿真设计，通常需要经过多个步骤，不仅效率较低，最终效果也难以得到保证，在此背景下，有关人员指出应将开发有限元软件的工作提上日程，以此来弥补常规软件所存在不足。有限元计算所依托基础为三维模型，对模型进行建立时，有关人员应对存储规律引起重视，充分利用产品数据库所存储各项参数完成计算工作，确保所建立分析模型能够发挥出应有作用。随后，再借助所建立模型进行计算，将计算所得数据以较为直观的方式进行展示。

2 有限元软件开发

以厂家所提供图纸为依据，对转向桥所适用计算模型进行建立。考虑到转向桥多为对称结构，除特殊情况外，均可将整体的1/2视为计算模型，在保证计算精度和有效性的前提下，对局部进行相应的简化[1]。

2.1 建立模型

由于转向桥内部往往无须搭载制动器，在建立模型时，通常不需要考虑车轮所承受切向力，而是将重心放在侧滑所产生横向力、垂直力上。在确定计算载荷时，应对不同工况所表现出特点加以考虑，转向桥常见工况如下：

其一，侧向力最大。简单来说，就是叉车处于空载转向工况时，受离心力影响，车轮往往会呈现出临界侧滑的状态，对侧向力进行计算的公式为：

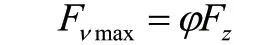
其二，垂直力最大。空载叉车通过凹凸不平的路段时，其内部将产生一定动载荷，使得垂直反力快速增加[2]。由此可见，垂直力极易受到轮胎弹性、行驶速度还有路面情况的影响，相关计算公式为：

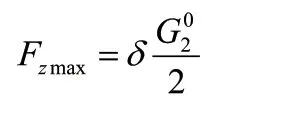
2.2 开发前处理模块

基于转向桥示意图对网格进行划分的关键是对物体进行离散化处理，利用15节点或是20节点对转向桥进行填充，曲面可借助空间插值函数做拟合处理，保证节点编号可达到带宽最小的要求，这样做能够在极大程度上缩短计算时间。为确保计算所得结果准确，有关人员选择将1/2转向桥划分成2666个节点、分属1524个单元，同时该网络共包括16层，各层均有计算模式对应[3]。

对结构较为复杂的转向桥而言，在划分网格的前提下，对各节点编号和对应坐标进行快速确定的难度极大。考虑到节点标号、对应坐标均属于原始数据，通常与几何数据、工程数据间存在紧密联系，有关人员指出，前处理的主要任务是准确生成集合数据。本软件以前处理模块为载体，新增了参数化设计的相关功能，同时强化了模块和PRO/E、ANSYS等软件的适配性，确保在利用上述软件建立模型的过程中，该模块能够充分发挥出采集、存储相关数据的功能。此外，还开发了负责修正数据的程序，旨在降低对构件进行前处理的难度，使前处理所取得效果更加理想。为保证所建立模型符合项目要求，有关人员决定参照前处理方法对力学模型进行建立，通过对比现有方案的方式，确定可最大限度满足项目要求的模型。

2.3 开发后处理模块

在有限元计算期间通常会形成海量数据，要想降低对比多个方案的难度，关键是要保证计算结果以十分醒目且直观的形式被呈现出来。后处理的关键，便是充分利用现有技术，对应力图、变形图、等值线图或是渲染图进行绘制，通过直观表达计算所得数据的方式，为后续检查工作的开展提供便利。

在对转向桥刚度、强度进行计算期间，本软件能够凭借OPENGL库和可视计算，高效完成编写后处理程序的工作，同时保证所编写程序可提供结果处理、变形显示以及绘制应力曲线等功能，通过提高处理效率的方式，减少该环节需要花费的时间[4]。

对后处理强度进行分析所遵循理论为第四强度理论，计算公式如下：

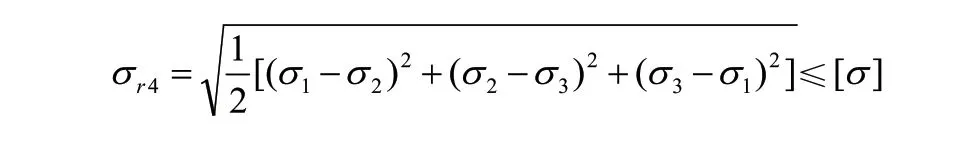
在该公式中，σ1代表第一主应力。σ2代表第二主应力。σ3代表第三主应力。[σ]代表允许应力，转向桥的主要材质为钢，而钢的允许应力约为293MPa。

3 软件应用实例说明

内燃叉车所配备转向桥多通过钢板焊接所得，运行期间往往需要承受侧向力、纵向力和垂直力，其工况的复杂程度有目共睹。在进行有限元分析时，有关人员决定先简化模型，假设桥体所用材料为均质、连续材料，同时符合完全弹性体的条件，在此基础上，对有限元软件进行使用，所涉及内容如下：

3.1 受力分析

3.1.1 空载静止。处于空载静止工况的叉车，其内部转向桥对应等效应力的最大值在18.8MPa左右，多数应力均位于桥体焊接点周围，纵向（Z向）位移最大的构建为轴套，相关数值在0.0019mm左右。

3.1.2 空载急刹。空载叉车由高速行驶状态切换成紧急刹车状态时，转向桥对应等效应力的最大值为18MPa，多数应力均分布在钢板焊接区域，轴套附近出现明显位移，位移相对值在0.0017mm左右[5]。由此可见，静态工况下，转向桥变形、等效应力值均未达到屈服极限，这表示转向桥强度能够达到行业标准。

3.1.3 空载转向。处于空载转向工况的转向桥，其等效应力最大值为19MPa，略大于空载静止工况，钢板焊接区域所承受应力较多，轴套附近所出现位移情况较其他区域更加明显，位移距离在0.0057mm左右。

3.2 模态分析

以静态分析模型为落脚点，借助ANSYS软件对结构模态进行计算，在此期间，不需要考虑阻尼所产生影响，只需将预应力开关打开，便可完成后续的模态计算等工作。本文所分析转向桥的参数如下：

表1 转向桥基本参数

对其固有频率进行计算所得结果如下：

表2 频率取值

上图共包括前十阶振型，其中，1阶是指转向桥两侧分别沿Z振动；2阶是两侧均沿Z振动；3阶是指两端均沿Y振动；4阶是指两侧分别绕Z转动；5阶是指两侧均绕Z转动；6阶是指两侧均绕Z、X转动且转速相同；7阶是指桥体绕Z转动；8阶同样是指桥体绕Z转动，但其振型较7阶略大；9阶是指桥体绕Y转动；10阶是指桥体绕Y、Z转动。

研究表明，转向桥对应1阶频率取值是313Hz，此时，路面激励频率处于低阶频率状态，其空间频率取值往往集中在0.2～2.0c/m间。对空间频率进行转化，可得出“时间频率处于1～20Hz”的结论，这表示1阶频率并未处于额定频率范围内，换言之，行驶状态下的叉车并不会导致桥体出现共振，加之多数位移均处于轴套附近，这说明叉车对转向桥在刚度方面所提出要求较为严格。

3.3 零件应用

3.3.1 桥体。有关人员利用分析系统对某叉车所配备铸钢转向桥进行了模拟。很长一段时间内，转向桥均以钢为主要材质，在本软件的辅助下，有关人员成功研发出了铸钢转向桥，其性能较钢转向桥更为突出。

图1 桥体模型

3.3.2 转向销。转向销主要材质为20Cr钢，将其强度换算成应力，最大值约为278MPa，可达到项目所提出要求。

3.3.3 转向节。该叉车转向节材质为45#钢，对应网格模型如下：

图2 转向节网络模型

将节点强度换算成应力值，计算所得数据均在264MPa左右波动，未超出允许范围，与使用要求相符。

4 结束语

通过上文的分析可知，在对叉车进行设计期间，有限元软件的作用主要是评估方案是否可行。基于计算机技术对相关系统或程序进行开发，可促使有关人员快速完成分析零件的工作，针对分析过程中所发现问题，对设计方案进行调整。事实证明，本文所开发有限元软件在拓展性、实用性等方面均具有突出表现，将其用于零件、叉车设计，一方面可保证设计需要得到满足，另一方面可使产品质量得到显著提高。未来有关人员应将工作重心向其倾斜，通过定期升级现有软件的方式，确保其所具有优势能够得到更加充分的发挥。