我国行业投入产出网络结构与资产收益率关系研究

袁 强 张自力 陈 姝 赵学军1北京大学光华管理学院北京 100871 嘉实基金管理有限公司北京 10000

引 言

在经济系统中，各个行业非孤立存在，因物质传递和信息交互，与其他行业相互连接，彼此构成复杂的网络系统。经济网络的拓扑结构复杂，行业间连接数量和紧密程度具有差异，对其他行业的风险传导和波及程度互不相同，体现了其所处经济系统位置的重要程度。在资本市场中，收益率反映了资产承担风险的水平，经典的资本资产定价模型（Capital Asset Pricing Model，简称CAPM）表明，市场组合收益率能很大程度解释风险资产的收益率，通过衡量风险资产收益率与市场组合收益率的联动关系，可以测度资产在资本市场中对系统性风险的暴露程度。目前，从资产间关联关系分析定价问题的研究不多，尤其是关注于行业间网络关联对其在资本市场表现的主题有待探索。已有文献中较有代表性的是Aobdia等（2014）［1］开展的关于美国行业关联与资产收益的研究，认为经济系统中越中心的行业在资本市场中暴露的系统性风险越大。但文章中行业关联网络的建立将行业间直接消耗和直接分配的关系进行综合，未区分行业在实体经济中发挥的供给和需求等不同功能，且以特征向量中心度描述行业在网络中的核心程度，在直观理解上也相对抽象。

本文在相关研究基础上，测度我国各行业从供给和需求等不同角度看，在经济网络中的位置是否不同？从动态年份上看，各行业的重要性排序是否有显著变化？对于我国而言，行业基于供需关系体现的系统重要性，能否解释行业在资本市场中承担的系统性风险？如果可以，供需角度下哪个指标的解释力度更好？

1 文献综述

对行业网络的定量分析和关键部门识别研究方面，很多学者将国家和区域的投入产出表与复杂网络分析方法结合进行分析。上世纪30年代，美国俄裔科学家列昂惕夫提出了投入产出表，记录经济系统中行业间生产消费关系。投入产出表的构成可分为3个象限，其中第二象限显示了各个行业中间投入和中间产出的数值关系，反映了各行业基于投入产出关系的连接状态和紧密程度。对于行业投入产出关系的定量描述，常见有直接消耗和完全消耗系数、直接分配和完全分配系数等指标，分别反映列昂惕夫模型中行业需求和供给的关联关系；Ditzenbacher等（2005）［2］综合完全消耗系数和完全分配系数反映的关联效应，计算两个系数的平均值，提出了行业之间的关联度系数概念。对于投入产出表的应用，学者们结合复杂网络方法讨论行业间的关系及经济结构。赵炳新（1996）［3］利用山东省62个部门关联关系，以及王茂军和杨雪春（2011）［4］以四川省67个制造行业连接情况，分析了省域经济的产业关系和结构特征。黄祖南和郑正喜（2021）［5］则利用2017年我国投入产出表，构造供给推动的前向关联和需求驱动的后向关联关系，构建产业有向有权关联网络，发现相比于基于威弗系数的无向无权网络，权重和方向的引入能更好地识别产业结构和经济系统中的关键产业部门。

对于产业部门重要性的计算，一般基于投入产出关系的行业网络，计算各个行业节点的网络中心度，表征行业在经济活动中占据的位置，以及对经济系统的重要性（汪云林等，2008）［6］。对网络中心度的描述，可分为点度中心度（Degree Centrality）、中介中心度（Betweenness Centrality）、接近中心度（Closeness Centrality）等常用指标（叶堃晖和袁欣，2018）［7］，或通过刻画网络节点时空距离定义相对中心度等特定指标（张自力等，2020）［8］。对于有向连接的复杂网络，点度中心度的计算还可根据连接方向区分入度（In－degree）和出度（Out－degree）概念（赵构恒等，2020）［9］。

对于行业间网络关联与经济金融表现的研究，Alhern（2013）［11］利用美国1997年投入产出表，发现产业关联越强，越可能出现并购活动。Alhern和Harford（2014）［12］通过指标对比发现，特征向量中心度在描述经济冲击对行业网络的传播效应方面表现效果更好。Boni和Womack（2006）［10］发现在金融市场中，行业因分析师信息而产生关联，资产价格会受关联关系传导影响。Aobdia等（2014）［1］利用1997年美国投入产出表，构造特征向量中心度对美国行业核心程度进行定量识别，发现特征向量中心度越高的行业，其组合收益率与市场组合收益率回归的R方越高。对于行业金融风险的测度，包括Aobdia（2014）［1］、王建斌和王少剑（2014）［13］、徐顺青等（2019）［14］、韩焯林等（2019）［15］用到了常见的CAPM模型进行定量描述。该模型由Sharpe（1964）［16］于上世纪70年代提出，奠定了现代金融理论的基石，并被国内外学者广泛运用于资产定价研究中。但综合而言，目前从我国行业关联角度出发分析行业定价的研究探索还较少。

本文研究我国行业中心度与资产收益率的关联，与以往研究的不同主要表现在，区分了行业在经济系统中供给与需求等不同功能，开展了多元指标对行业系统性风险的相关性检验，并对结果增加了动态时间上的稳定性分析，将对基于行业投入产出关系的资产定价研究提供有益参考。此外，以A股市场作为研究对象，也丰富了行业定价问题在我国资本市场中的研究探索。

2 研究方法

本文研究的方法主要分3个部分：（1）基于投入产出表分别从需求和供给的角度计算行业间的关联关系，从而反映各行业在经济系统中对其他行业的后向需求拉动效应、前向供给推动效应以及综合的供需关联效应；（2）基于上述关联关系构建行业复杂网络，多角度地表征行业的中心度并排序，进而从供需多方面体现行业在经济系统中的重要性；（3）计算各行业收益率在CAPM模型的回归R方，并检验行业网络中心度指标与R方间的相关关系。具体分析步骤如下。

2.1 基于投入产出表的行业关系识别

在我国，第一张投入产出表于1987年编制完成，一般每逢尾数为2和7的年份编制一次基本表，尾数为0和5的年份编制延长表，而基本表相比延长表对行业的分类尺度更细致。按照《国民经济行业分类KGB／T4754－2017》分类标准，我国2012年、2017年、2018年投入产出表的行业总数分别为139、149、153个。为了获取行业收益率数据，本文匹配投入产出表行业与申万二级行业分类，相应地对投入产出表的部分行业分类做了整合，具体对应结果略（由于篇幅有限，留存备索）。

本文利用我国2012年、2017年、2018年发布的投入产出表，分年份计算完全消耗系数、完全分配系数、关联度系数，体现行业间关系状态和连接强度［17－19］。经申万二级行业对应合并后，2012年、2017年和2018年行业投入产出网络分别具有90、96和98个行业节点。对完全消耗系数矩阵、完全分配系数矩阵、关联度系数矩阵的计算，公式如下所示：

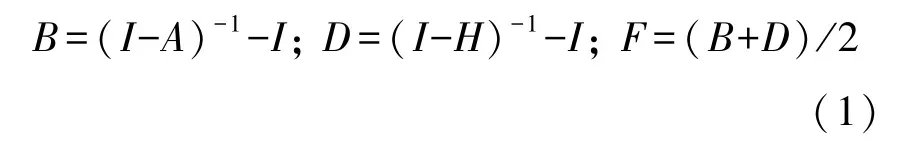
其中，B为完全消耗系数矩阵，A为直接消耗系数矩阵，A中元素aij＝xij／xj，xij为行业j对行业i的消耗量，当i和j相等时，表示行业对自身的消耗，而xj为行业j总的消耗量；完全消耗系数bij反映了行业j提供1单位最终产品，对行业i产品的直接消耗和间接消耗之和；D为完全分配系数矩阵，H为直接分配系数矩阵，元素hij＝xij／xi，xij为行业i对行业j的分配量，当i和j相等时，表示行业对自身的分配，而xi为行业i总的分配量；完全分配系数dij反映了行业i提供1单位最初投入，直接和间接分配给行业j产品之和；I为单位矩阵，F为关联度系数矩阵，Fij体现了行业i对j完全消耗和完全分配关系的叠加。

为具体说明上述3个矩阵中元素值对于行业间关系描述的实际内涵，这里以完全消耗矩阵为例，展现行业对经济系统产生的需求效应。

上式减去单位矩阵后，则有B＝A＋A2＋A3＋…，表示经济系统无穷级的消耗对经济的拉动影响。令A为3×3矩阵，如下：

A2为经济系统中行业间一次传导的间接消耗系数，a11a11＋a12a21＋a13a31是行业1通过一次传导对本行业的消耗，具体包括：a11a11为行业1通过消耗本行业间接对该行业的消耗影响，a12a21是行业1通过消耗行业2进而拉动行业2对行业1的消耗，a13a31是行业1通过消耗行业3进而拉动行业3对行业1的消耗。A2中其他元素也是如此。

而当经济系统二次、三次直至无限多次传导消耗，则有了A3、A4直至Ak（k＞0）的间接消耗矩阵。所以，完全消耗矩阵B表示行业间直接消耗加间接消耗的综合，矩阵元素反映了行业两两之间在经济系统中总消耗关系。

2.2 网络视角的行业中心度刻画

在建立行业间的复杂网络时，以行业为节点，将上述3个矩阵作为邻接矩阵，进行行业节点连接，而节点之间的连接则基于矩阵数值赋予权重，分别构建3个年度下行业消耗关联、分配关联、供需关联的有向有权复杂网络，即经济系统的消耗网络、分配网络和综合关联网络。图1显示了基于2018年投入产出表中关联度矩阵构建的行业综合关联网络，网络节点为行业名称，行业间因关联系数而形成有向有权连接①。在我国投入产出行业网络中，除个别行业连接数量较少外，绝大多数行业均与其他所有行业发生全连接关系。

图1 基于2018年投入产出表的行业综合关联网络示意图

因所构建的行业供需复杂网络中行业节点连接具有方向特征，同时考虑到完全消耗系数、完全分配系数以及关联度系数已经包含了行业之间的直接和间接关系的总和，反映了行业间在网络路径中直接传导和间接传导的总影响，这里利用点度中心度相较于其他中心度指标对行业重要性的描述更为合理。

对于消耗网络、分配网络和综合关联网络的行业重要性分析，通过计算消耗网络中各节点入度，反映行业在需求拉动效应中的重要性；计算分配网络中各节点出度，反映行业在供给推动效应中的重要性。同时，考虑到关联系数综合了供给和需求双重效应，分别计算综合关联网络中各节点的出度和入度，反映行业间供需综合效应的网络含义。

其中，Siin、Soiut分别为行业的连接关系的入度中心度和出度中心度；wij为行业i指向行业j的关系权重，在本文研究中分别为B、G、F中的矩阵元素。

2.3 行业中心度与行业资产定价关系

为识别资产的系统性风险，本文利用经典的CAPM模型，计算各个行业收益率与市场组合收益率的联动关系。考虑到与投入产出表中行业分类的匹配程度，这里本文以申万二级行业分类中64个行业作为研究样本②，分别搜集2007～2012年、2013～2017年以及2018～2020年3个时段的行业指数周收益率和作为市场组合收益率的万德全A周收益率，将银行1年期定期存款利率的周收益率作为无风险收益率。CAPM模型解释了风险资产与市场组合的线性关系，资产与市场组合联动性越强，说明其承担的系统性风险更高。该模型计算表达式如下：

上式中ri，t为t时刻风险资产i的收益率，rf，t为t时刻无风险资产收益率，rm，t为t时刻市场组合收益率，βi是风险资产i的风险系数，ei，t为t时刻资产i收益率的随机扰动项。

这里使用统计指标R方，作为资产与市场组合联动的测度指标，取值范围为［0，1］。由式（7）可以看出，对于风险资产i，市场组合收益率对行业收益率解释力度越大，则R2i越高，表明行业对系统性风险的暴露程度越大。

其中，SSRi为风险资产i收益率预测数据与原始收益率数据均值之差的平方和，SSTi为风险资产i原始收益率数据与均值的差值平方和。var［×（rm，t－rf，t）］表示市场组合带来的总体变动，var（ei，t）表示行业特质性的变动，R2i与市场组合变动var［×（rm，t－rf，t）］呈现单调性。

为了表明R2与行业中心度S间的相关关系，利用皮尔森相关系数（Pearson Correlation Coefficient）进行测度。

其中，r为皮尔森相关系数，S为行业的中心度指标。

3 研究结果与分析

3.1 行业中心度排序及年际变化

基于消耗、分配以及综合关联网络的中心度分析，不同指标所描述的行业重要性排序有显著差异，但同一种中心度描述指标在年际间数值变化不大。下面以2018年计算结果为例，说明不同指标对于行业排序结果的差别。如表1所示，以关联入度升序排列，排名第1位的行业房地产开发在消耗入度、分配出度、关联出度中，分别排名在64、84、29的位置，而第2位的商务服务则在41、24、7位。对于关联入度排名较后的环保工程及服务在分配出度排名第8位和关联出度第20位。这反映了行业从供给和需求等角度，在经济系统中发挥的作用不同，也印证了本文从供需等多个视角观测行业重要程度的必要性。

表1 2018年各行业在不同指标下的中心度排序

而以关联入度为中心度测量指标，对经济含义的解释力度更强。参考黄祖南和郑正喜（2021）［5］的研究，选取中间消耗占比作为测量行业重要性的判断指标，商务服务、化学制品、半导体、钢铁等关联入度前5位的行业在中间消耗排名也位居前列，而其它3个测度指标与中间消耗量排名差距显著，如钢铁行业在中间消耗量排序位于第3位，而消耗入度、分配出度以及关联出度等分别排在第45、31、15位。对于中间消耗量排名靠后的社会工作、社会保障等行业，其在关联入度的排位名次也较后。这表明关联入度指标对于测度行业在经济系统的重要性有较好的表征能力。

从动态时间上看，我国经济系统中绝大多数行业的关联入度数值变化不大，经济结构相对稳定，部分行业的重要性排序在年际间有显著变化，如表2所示，半导体、通信设备等重要性连续上升，达到2018年的第3位和第8位，显示其对经济系统的拉动和分配作用在增强，这也较好地吻合了我国在这些科技产业中的投资及消费显著增长的趋势。对比2012年和2018年，高速公路、其他采掘以及煤炭开采等偏基建的行业则呈现下降趋势，分别降低10位、13位和11位，显示我国新时期基建对经济发展的拉动作用不及10年前的影响。

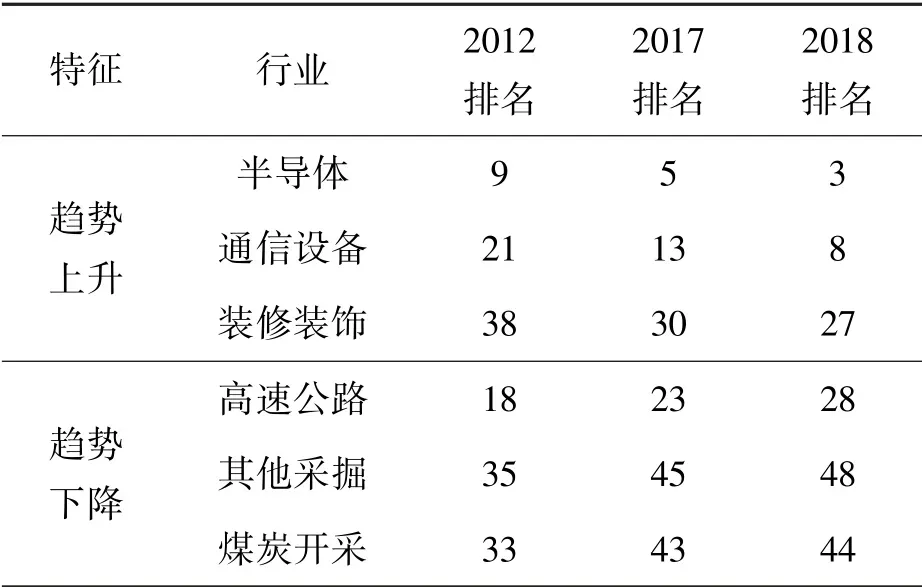
表2 2012年、2017年、2018年重要性变动显著的代表性行业

3.2 行业资产定价结果及与网络中心度关系

从2007～2012年、2013～2017年和2018～2020年3个时段整体分析（由于篇幅有限，具体对应结果留存备索），专用设备、通用机械、化学制品等行业R方较高，3年均值皆大于80%，说明这些行业暴露在市场中的系统性风险较大。保险、餐饮等行业与市场收益率的联动性较低，3年R方均值小于40%，与市场组合的联动性不强。

以变异系数对R方的年际变化进行测度，行业i的R方变异系数数学表达为CVi＝σ（Ri，t）／Ri，t。计算结果如图2所示，变异系数大于20%的仅有农业综合、装修装饰、运输设备、银行等8个行业。整体看，大部分行业的R方都较为稳定，说明在不同时期行业收益率与市场组合收益率联动程度变化较小，承担的系统性风险较为一致。

图2 3个时段下各行业R方的变异系数数值及累计比例

按中心度数值的分位数对行业进行分组，计算各组的行业R方均值并比较。如表3所示，关联度入度越大的行业组别，CAPM模型检验的R方越大，这说明行业的R方与关联入度存在正相关关系，两者呈现显著的单调性趋势。表3中关联入度四分组结果显示，3个年份数值也表明了关联入度对行业承担的系统性风险有较好的区分效果。由此可见，关联入度指标不仅可以体现行业在经济系统的重要性，且反映了其在资本市场承担的系统性风险，即经济系统中越重要的行业，在资本市场中与市场组合收益率的联动性越高。

表3 以关联入度指标三分组下各组R方的平均值

为进一步说明行业关联入度与行业资产承担的系统性风险程度，本文计算了3个时段下行业关联入度与R方的皮尔森相关系数。图3显示3个年份的r值均为正，说明R方和行业关联入度存在正相关关系，其中2013～2017年和2007～2012年的相关系数值为0.4左右，两者相关程度显著。2018～2020年度的相关性系数相对较低，可能是R方的计算样本相对少所引起，但得到的相关系数仍显著大于0。这也直接证明了行业关联入度指标对资本市场系统风险具有较强的解释力度。

图3 3个时段行业关联入度与行业收益率R方的关系

为探究关联入度指标是否对行业资产定价具有区分优势，这里将其与消耗入度、分配出度、关联出度3个指标进行对比。如表4所示，基于各时段下四分组分析发现，分配出度在4个组别的R方均值差异不大，以2018年为例，最高组和次低组值为0.625和0.635，消耗入度、关联出度等指标的次高组R方均值基本都大于其他组别，未体现单调性特征。由此可见，关联入度作为衡量行业承担系统性风险的指标，比其他指标更能描述行业承担资本市场系统性风险的程度，并在动态年份的测度上体现了较好的稳定性。

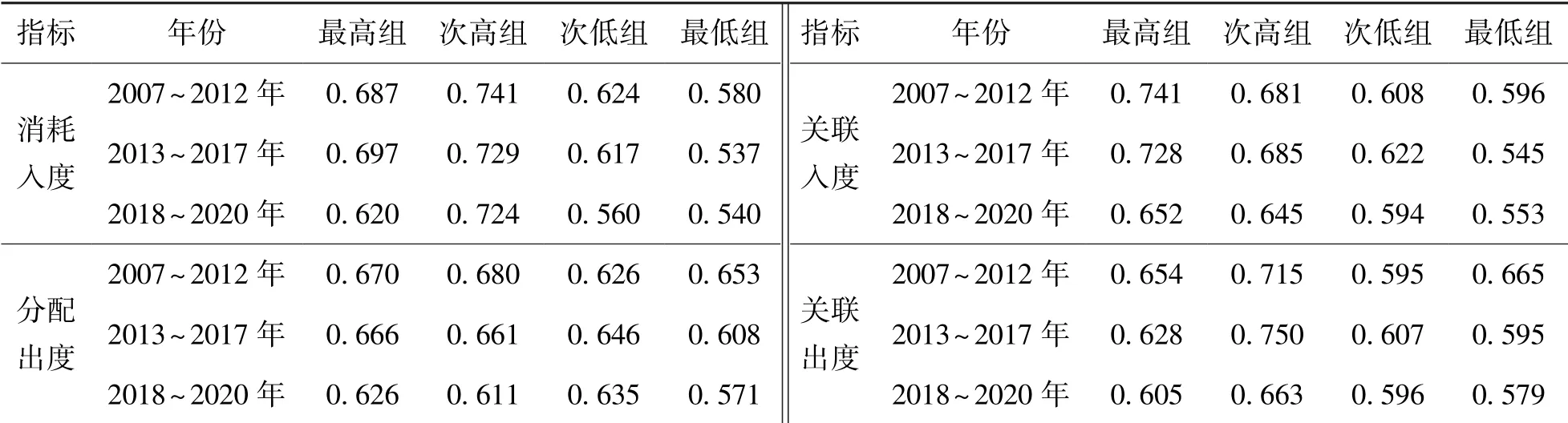
表4 各时段不同指标四分组下R方均值比较

4 结 论

经济系统中，行业通过生产供给和产品消费等贸易活动相互关联，形成彼此连接的复杂网络。在资本市场中，行业收益率表现出异质性特征，反映了行业承担的系统性风险并不一致。本文研究分析了各年份我国国民经济行业在经济系统中的重要性，探索其与行业承担的系统性风险之间的关系。

研究结果发现：（1）基于投入产出表与复杂网络技术构建的关联入度指标，可以反映行业在经济系统中的重要性，该指标显示，我国2012～2018年间，经济系统的行业结构有一定变化，半导体、通信设备等科技行业重要性上升，而基建类行业的重要性则有所下降；（2）基于资本资产市场定价模型，在2007～2012年、2013～2017年、2018～2020年3个时段，我国A股市场专用设备、通用设备、化学制品等行业R方较大，显示了其与市场组合收益率保持较强的联动性；（3）3个时段下，行业关联入度指标与行业R方有明显的正相关性，对行业系统性风险暴露程度有较好的解释力度，相比其他指标，对区分行业资产收益率表现有显著效果。研究结果中不同行业与市场收益率联动的异质性，对行业资产配置活动具有一定参考。此外，鉴于行业关联入度与R方的关联特征，建议政策部门可以通过定量行业在投入产出网络的中心度，识别和防范行业在资本市场中的系统性风险。

注释：

①线条箭头代表连接方向，线条越粗体现行业间连接权重越大，行业节点颜色越深代表中心度越大。

②3张投入产出表公布的行业数量略有差别，2012年投入产出表未包含一般零售、公交、互联网传媒等行业类别，收益率研究的行业样本为61个。