扩展有限元法在断裂力学相场模型中的应用

张子瑜，郝林

上海飞机设计研究院 载荷部，上海 201210

由于裂纹可能威胁到民用飞机主传力结构的完整性，进而威胁飞行安全，对裂纹扩展的模拟是疲劳及损伤容限分析的重要内容。扩展有限元方法(X-FEM)采用单位分解的思路，将单元形函数空间加以丰富，从而在不要求有限元网格与内部边界吻合的前提下模拟大量的物理问题，其在断裂力学领域的应用日趋广泛。Hansbo A和Hansbo P提出的幻影节点法(Phantom-node Method)能够在技术层面等效地执行X-FEM，此方法将被裂纹切割的单元复制后仅在被复制单元的真实域内对相关量(如刚度矩阵等)做局部数值积分。这种方法将传统X-FEM中添加额外自由度的需求替换为对网格的更改。

相场法在模拟裂纹扩展问题时则采取另一种思路，将表达破损区域的相场方程与力学方程耦合，从而使得裂纹可以自然扩展，使得计算裂纹的前进方向和距离不再必要。然而，由于相场法无法构建出清晰的裂纹断面，故该方法存在一些局限。例如，它很难模拟裂纹断面之间的接触及摩擦效应，也会使裂纹区域单元的局部刚度趋于0而导致求解困难。

在早期介绍水平集(Level-set)方法的文献[9] 中，X-FEM被用来模拟完全破坏的区域(即空洞)。相场法方面的研究者受到启发，使用幻影节点法将被相场等高线切割的单元做局部数值积分，并删去位于等高线内部的单元，从而模拟破损区域。本文同样将X-FEM与相场法结合，但提出一种构建清晰裂纹断面的替代方法：通过一定的算法，找到能够近似地连接相场值为1的所有点的单根轴线(即相场中线)，并通过X-FEM来实现相场中线对网格的切割。

另外，在以往构建相场中线的文献[11-14]中，研究者常连接位于相场等高线内部的最大球的球心来生成中线，但这些方法存在局限性，如过分耗时，或仅能解决静态裂纹问题等。鉴于此，本文利用相场等高线与辅助网格的交点，构建一种新的、效率更高的中线生成方法。

1 扩展有限元基本算法

幻影节点法不直接添加额外的形函数和自由度，而是在裂纹处创建重叠的单元。图1说明了幻影节点X-FEM的基本思路。当1个单元被裂纹完全切开后，创建2个子单元(或称为副本单元)，2个子单元将从原来的母单元继承不同的物理域，称此物理域为“碎片”(即图1右侧单元的阴影部分)。注意，图1中圆圈所表示的节点不属于单元碎片，因此它们被称为“幻影节点”。幻影节点处的数值解不重要，但可用于对物理域内某点的数值解进行插值。一般说来，一个子单元拥有的幻影节点将与其“兄弟”单元完全脱开。在2个子单元被创建后，所有新的自由度会被适当分配，且母单元将被删除。

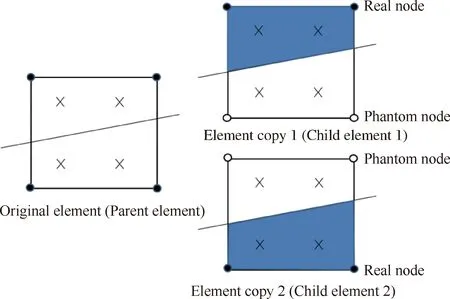
图1 幻影节点X-FEM中裂纹切割单元Fig.1 Elements cut with phantom-node X-FEM

原始的X-FEM法会采用分段积分方法对被裂纹切割的单元求积分。在幻影节点X-FEM中，只需在每一个子单元的物理域内进行积分。因为幻影节点法更易于被系统化地执行，所以更适合商用代码使用。在有裂纹分叉的情形出现时，此方法更显其优势。注意，文献[5]的方法只适用于整个单元被裂纹完全切割的情况。Rabczuk等则为幻影节点法开发出一种裂纹尖端单元，使得在进行静态裂纹仿真时，裂纹尖端可以位于单元内部。本文使用的幻影节点X-FEM切割单元的算法被称为“单元碎裂算法”，其在每一个时间步中的基本流程如下：① 更新相邻单元的信息；② 标记裂纹尖端处的单元；③ 标记新的切割点；④ 创建碎片；⑤ 从碎片创建子单元；⑥ 连接相邻的碎片和子单元；⑦ 清理母单元。

2 相场法在断裂力学中的应用

本文采用Miehe等提出的相场断裂力学模型。通常情况下，可以通过将总势能最小化，或使虚功率等于零，来获得控制方程的强形式:

+-=0

(1)

式中：为总应变能；为耗散能；为外力功。总势能为位移和相场的函数:

(2)

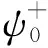
若不考虑防止裂纹愈合的方法，脆性材料的耗散能一般可被写为

(3)

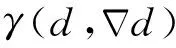
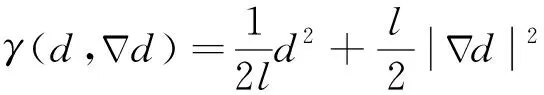
(4)

外力功则遵循传统的形式

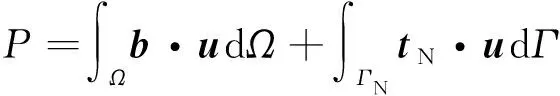
(5)

式中：为体积力密度；为单位面积的边界力;为位移场；Г为Neumann边界。

将式(2)～式(5)代入式(1)，并使用分部积分，可得如下强形式的控制方程：

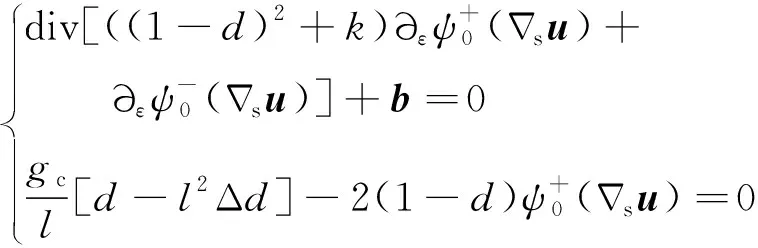
(6)

且满足边界条件

(7)

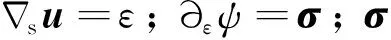
为了保证相场的不可逆条件，Miehe等对式(6)的第2个方程进行了改进，引入了1个的对偶变量及1个额外的约束方程。那么，相场断裂问题的控制方程可写为

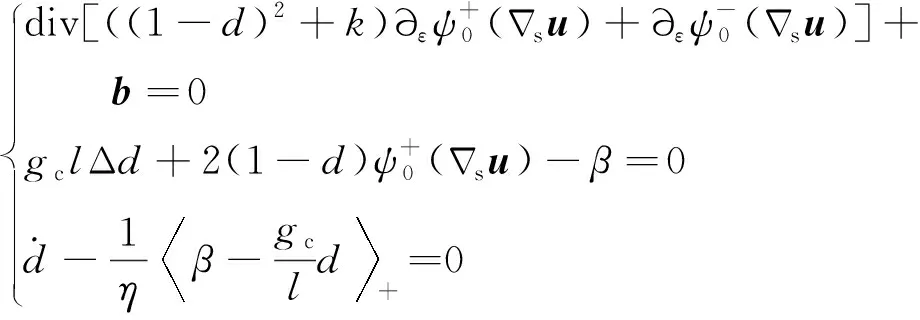
(8)

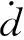
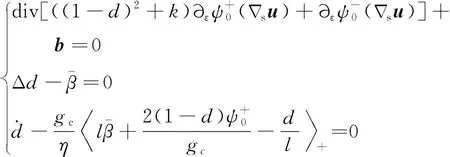
(9)

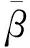
(10)

式(10)可使用有限元方法进行离散求解。

3 生成相场中线的方法

构建相场中线算法的核心思想为：创建一个比有限元网格粗的辅助网格，使其能够覆盖求解域。之后，求出相场等高线与辅助网格的交点，并将基于这些交点生成能够表征相场中线的线段。其算法可分为2步：

1) 对于每一个辅助网格单元，求出中线交点及其方向向量。其中，中线交点即为相场中线与辅助网格单元边的交点，而其对应的方向向量代表着相场中线的方向。在执行本步的过程中需遍历所有辅助网格单元。

2) 在每一个辅助网格单元中，适当地将中线交点相连来创建单元内的中线线段。那么，完整的相场中线将由所有单元的中线线段组成。

注意，相场等高线由常规的行进正方形(Marching Squares)算法生成。此外，使用排序算法将组成等高线的小线段沿着逆时针方向排列存储。图2为相场云图及=0.9所对应的等高线示意图。值得一提的是，即使在行进正方形算法中将相场值设置为1，通常情况下也无法得到1条单一的等高线。这是因为，有限元方法的离散性使其无法捕捉到相场值严格等于1的尖点。

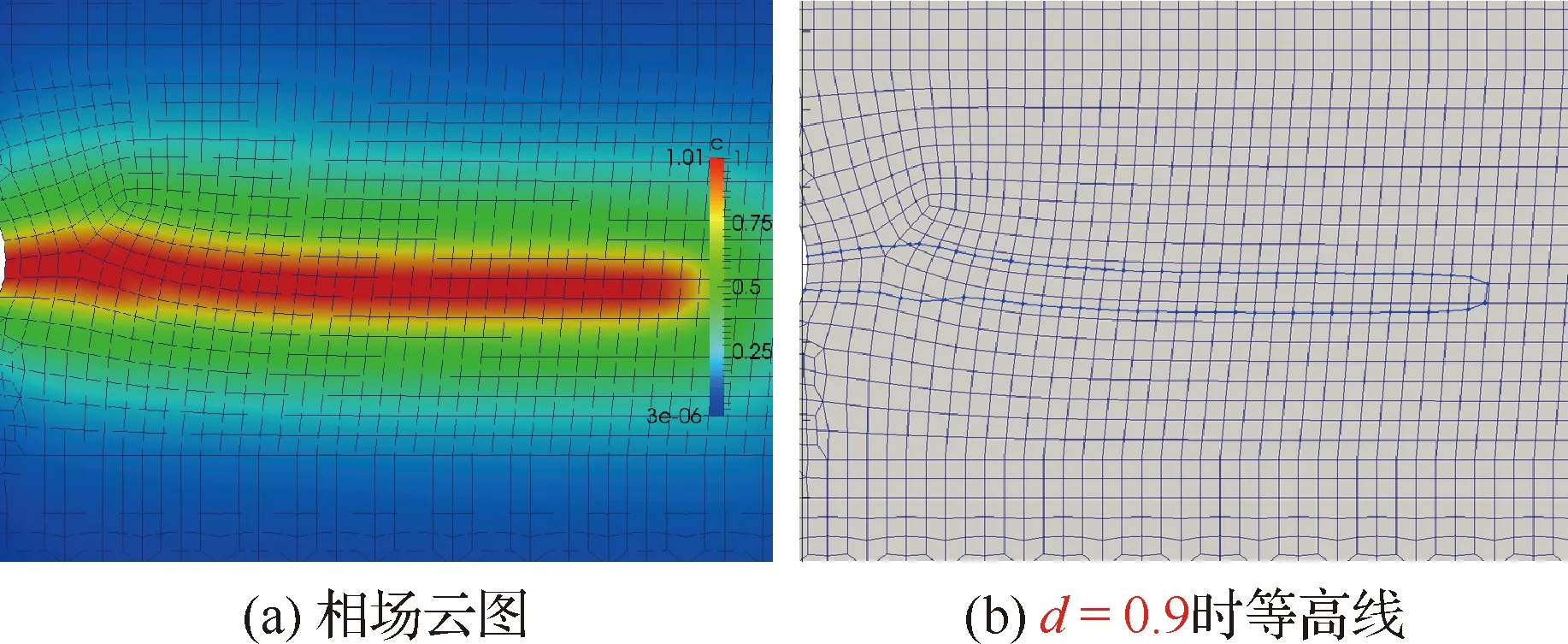
图2 相场云图及其对应的等高线Fig.2 A phase-field and its isocontour

3.1 计算辅助网格单元的中线交点

在计算相场中线与辅助网格单元的交点时，通常有3种情况需要处理，现论述如下。

辅助网格单元的边和相场等高线只有一个交点。

以图3左下角的单元为例来说明算法。当遍历此单元的所有边后，可以发现右侧的边与相场等高线只有1个交点，且此单元右上角的节点距离这个交点最近。那么将与这个节点相连的所有单元边(这些边形成1个“十”字)与相场等高线相交，则可得到4个交点。最后，将这4个点的坐标取平均后即得相场中线与单元边的交点(即图3中的点5)。这一过程被称为“节点块搜索”。

图3 情况1示意图Fig.3 Illustration of Case 1

相场中线与辅助网格交点的方向向量可基于相场等高线与辅助网格交点的切向量来计算。如前所述，由于组成相场等高线的小线段以逆时针排列存储，故可将与辅助网格单元边相交的相场等高线小线段的方向作为等高线交点的切向量。取第1个等高线交点和最后一个等高线交点的切向量，将二者平均后即可得到相场中线与辅助网格交点的方向向量。在图3中，相场中线交点的方向向量即为0.5(-)，其中，为等高线交点1的切向量，为等高线交点4的切向量。注意，相场中线交点方向向量的方向与等高线交点1切向量的方向一致，因为后者的方向通常代表了裂纹扩展的方向。

辅助网格单元的边和相场等高线有多个交点。

以图4为例，考察左上角的单元，其左侧的边与相场等高线有2个交点，故只需将2个交点的坐标取平均即得到相场中线交点。对于右侧的边，可以找到3个等高线交点，标记为编号1～3，如图4所示。注意，编号1～3事实上也代表了相场等高线小线段在数组中的存储顺序。将这3个交点按照距离单元右侧边第1个节点由近及远的顺序排序后，可得数组{交点2, 交点3, 交点1}。之后，遍历交点对，依次计算交点2、3的中点CutNode23和交点3、1的中点CutNode13。鉴于CutNode23位于相场等高线围成的区域之外，故只有CutNode13可作为相场中线交点。此外，等高线交点2未与其他交点形成交点对，故它被称作孤立交点，可调用节点块搜索来计算其对应的相场中线交点。与情况1类似，CutNode13的方向向量可由0.5(-)计算。

图4 情况2示意图Fig.4 Illustration of Case 2

还可以判断相场中线方向向量与辅助网格单元的关系，即，它是在“进入”“离开”或者“掠过”当前的辅助网格单元。具体的判断准则为：若相场中线交点方向向量与辅助网格单元边法向量的点乘为正，则方向向量“离开”；若点乘为负，则方向向量“进入”；若方向向量与2个单元边都有点乘，且二者符号相反(如图4左下角单元中右上节点附近的相场中线交点)，则方向向量“掠过”此单元。

在图4中，虽然辅助网格单元边与相场等高线只有3个交点，但情况2的算法可推广到更多交点的情况。

找到辅助网格单元内部的相场中线交点。

裂纹的起始点通常位于辅助网格单元的内部，称作尖端交点，如图5所示。如果一个辅助网格单元与相场等高线只有一个中线交点，搜索等高线在单元内部的缺口，那么缺口的中点即为尖端交点。

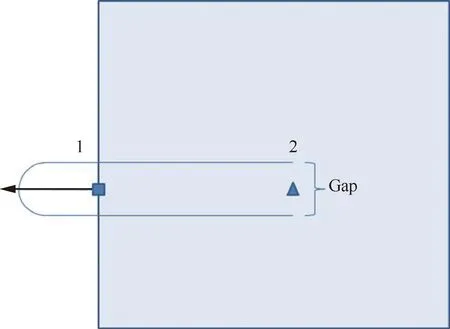
图5 情况3示意图Fig.5 Illustration of Case 3

总之，上述算法可使我们找到每个辅助单元上的中线交点以及每个中线交点的方向向量和方向向量的属性(即“离开”“进入”或“掠过”)，方向向量是中线线段局部方向的表征。有了这些信息后，就能够生成中线线段。

3.2 生成辅助网格单元的中线线段

寻找辅助网格单元内中线线段的方法与单元中线交点的数目有关。如果某单元只有2个中线交点，则这2个点可直接相连以创建表征裂纹的线段。若某辅助单元有3个中线交点，且其中1个是进入状态、另外2个是离开状态(简称为“一进两出”)，则首先找到3个中线交点的方向向量的交点。若3个向量的交点位于此辅助单元内部，则此交点即为裂纹分叉点，且裂纹线段可通过连接分叉点和3个中线交点来建立(见图4)。若3个向量的交点位于此辅助单元外部，则将进入状态的中线交点作为分叉点。若3个中线交点的状态并非“一进两出”，则使用下面介绍的对齐算法。

对于拥有大于等于3个中线交点的辅助单元而言，可使用对齐算法确定两两相连的中线线段。对齐算法执行时，程序遍历所有中线交点。对于任一中线交点，尝试将此点与其他所有的中线交点相连。对于每一个连接线段，程序计算此线段与两端中线交点处方向向量的夹角，其中较大的角被定义为对齐指标，用于衡量中线线段与两端方向向量的一致程度。对齐指标的定义为

=max(,)

(11)

=

(12)

式中：=1或2；=-；、分别为中线线段两端中线交点的坐标向量；为中线交点处的方向向量。若某中线交点的某一个中线线段的对齐指标最小，则此线段为唯一有效的中线线段。为了详细解释，考察图6中的中线交点3。在所有可能的中线线段3-4、线段3-1和线段3-2中，线段3-4及其2个端点的方向向量的对齐程度最好。因此，线段3-4是中线交点3唯一有效的中线线段。

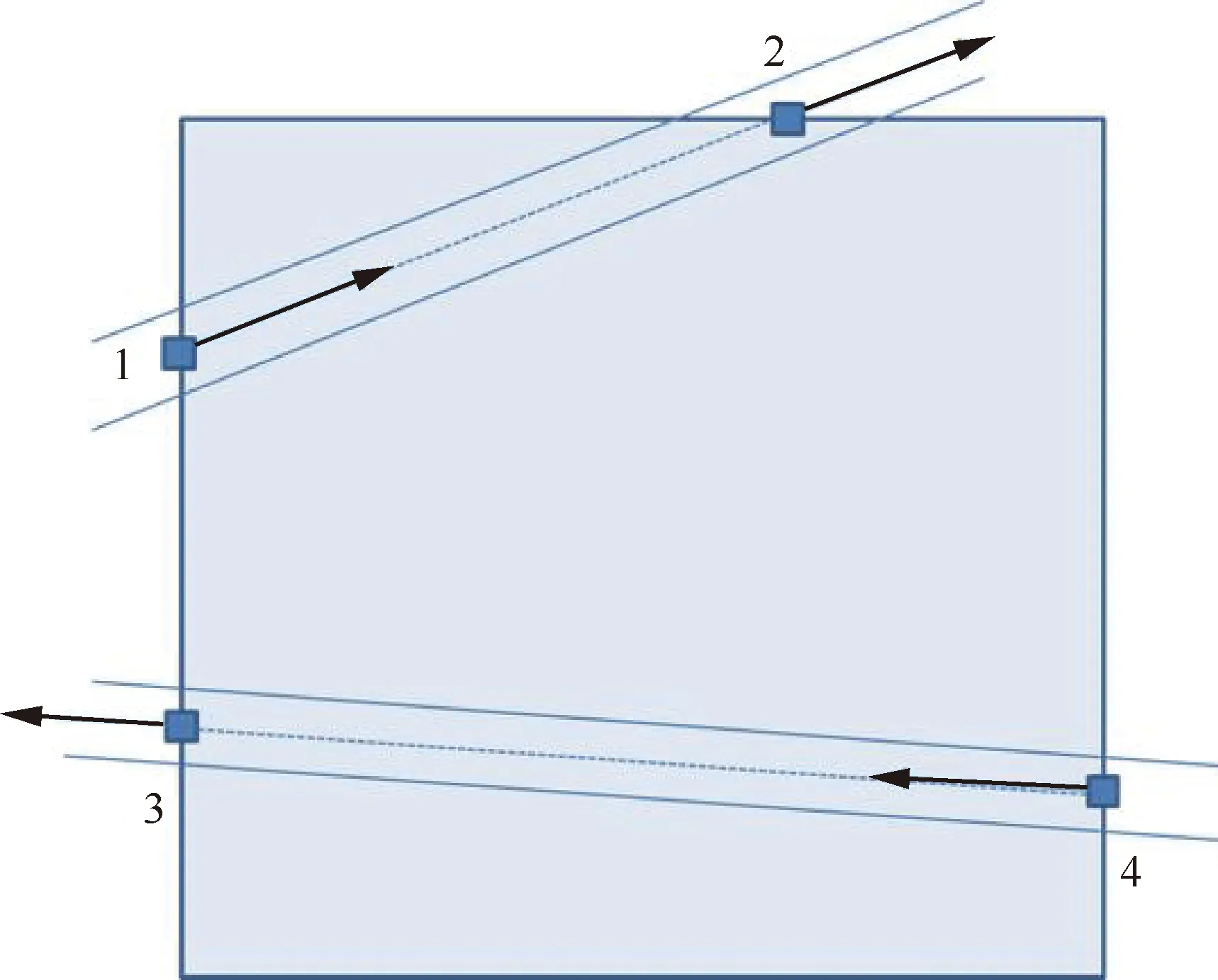
图6 对齐算法示意图Fig.6 Alignment algorithm

当某辅助网格单元的中线交点数量为奇数时，上述算法可能导致某中线交点同时从属于多条中线线段。若对这类中线交点再次使用对齐算法，可使仅拥有最佳对齐指标的中线线段被保留。

3.3 添加新的中线线段

随着仿真的进行，相场等高线会动态变化。当有新的中线交点生成时，程序会尝试将新中线交点的方向向量和已有的中线线段相交来生成新的中线线段，如图7所示。在图7中，线段1-2是已经存在的中线线段，中线交点3是新的中线交点。程序计算中线交点3处方向向量与中线线段1-2的交点(即图7中的点4)，并将其与中线交点3相连，从而生成了新的中线线段。

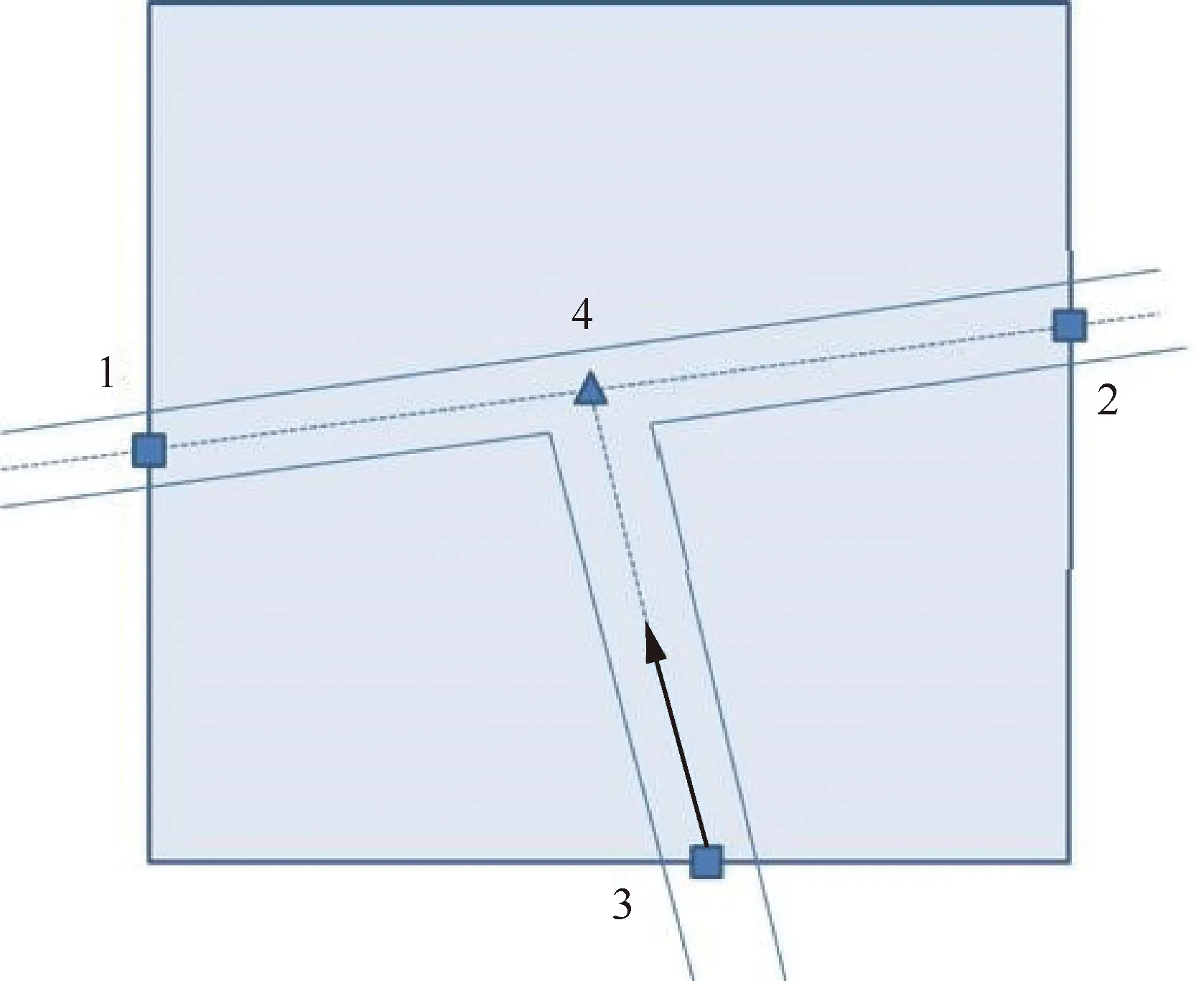
图7 生成新中线线段的过程Fig.7 Process of computing new medial segments

4 数值算例

4.1 静态等高线的中线

图8所示为一个给定的静态等高线的中线生成结果。在本例中，辅助网格被巧妙处理以创造更多的棘手情况，从而测试程序的健壮性。图8中，中线线段以红线表示。特别地，单元9左上角中线交点的计算即为3.1节中节点块搜索的典型例子，而单元22的中线交点符合“一进两出”，其分叉结构由图4所示的方法生成(详见3.2 节)。此外，使用对齐算法生成了单元21的中线线段。

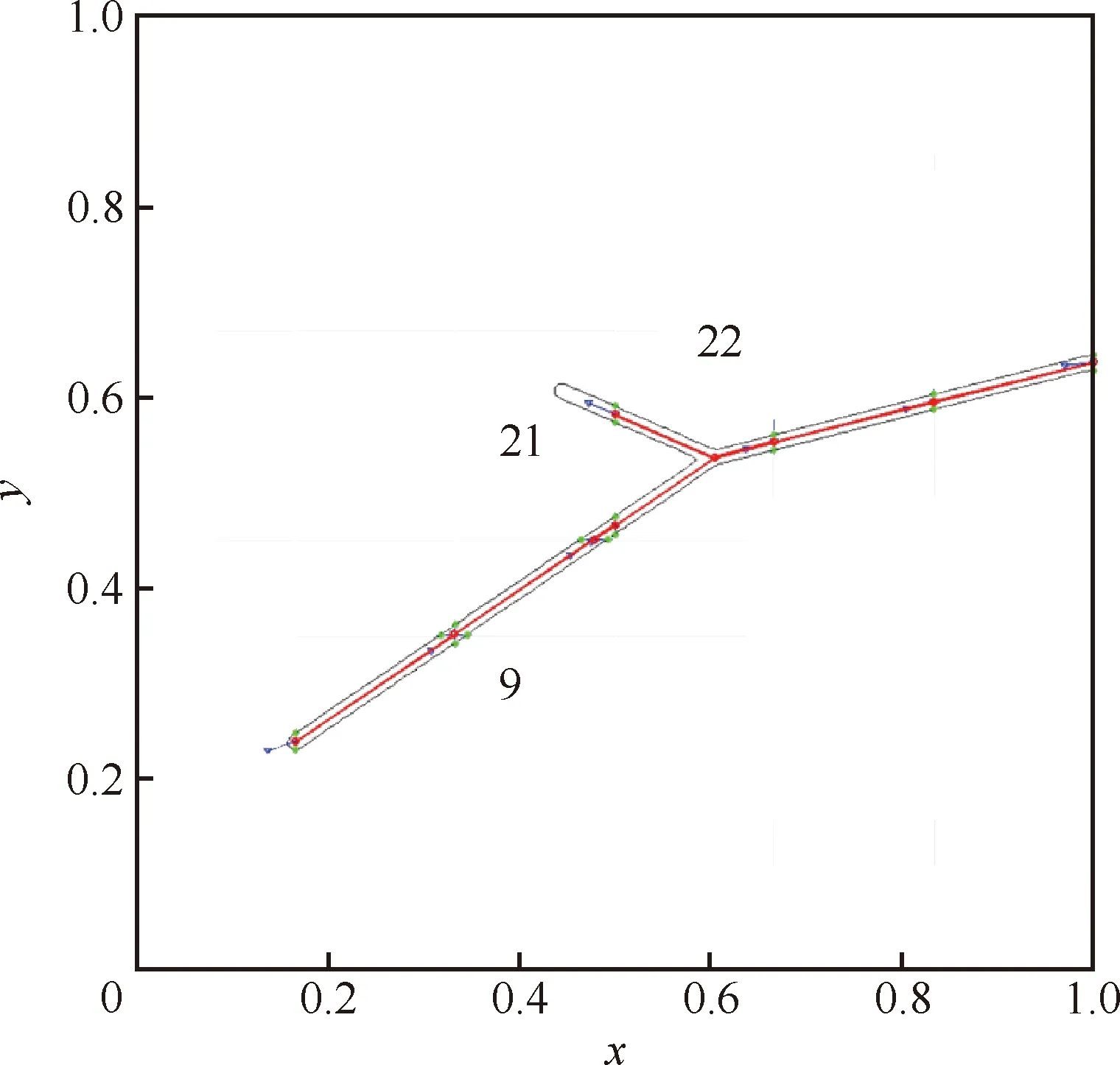
图8 静态等高线的中线生成Fig.8 Medial-axis generation of a static isocontour

4.2 动态等高线的中线

4.2.1 裂纹融合

设计1个二维断裂数值算例：1个1 mm×1 mm 的方形板在=0～0.00 308 203 s的时间内受拉，拉力施加于上部边界。随后，上部边界停止受拉，转而在右侧边界受拉。

上部边界的位移边界条件为

(13)

右侧边界的位移边界条件为

(14)

将材料设置为各向同性，杨氏模量=208 kN/mm，泊松比=0.3，本构阈值=10kN/mm，相场特征尺度=0.03 mm，人工黏性=10(kN·s)/mm。使用开源平台MOOSE(Multi-physics Object Oriented Simulation Environment)进行仿真，结果见图9。可见，红色的线段所示的相场等高线中线能够随着相场等高线适当地扩展，且捕捉到了裂纹融合的过程。

图9 二维融合裂纹的相场云图及其中线Fig.9 Phase-field contour and medial-axes of 2D merging cracks

4.2.2 裂纹分叉

4.3 使用相场中线切割网格

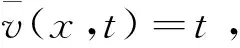
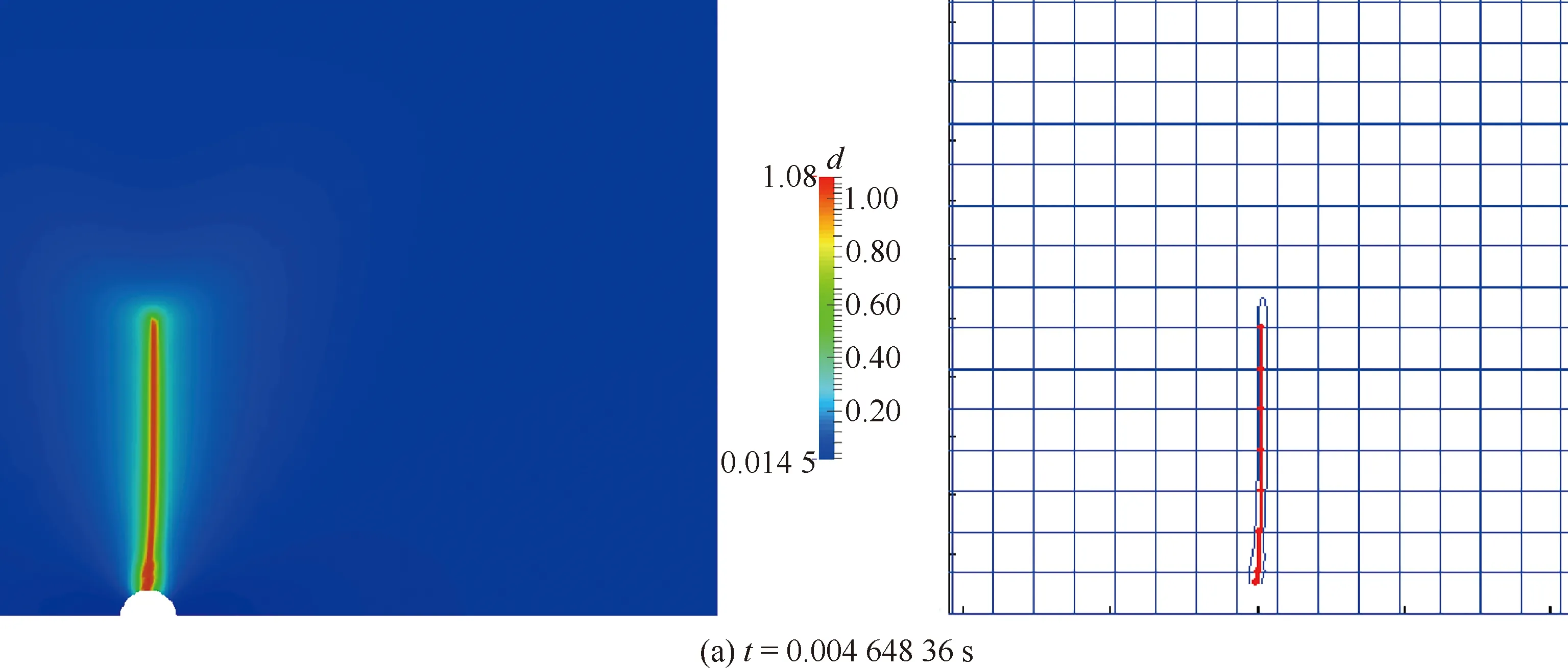
图10 二维分叉裂纹的相场云图及其中线Fig.10 Phase-field contour and medial-axis of a 2D branching crack

图11 使用单条裂纹的相场中线切割网格Fig.11 Mesh-cutting using medial-axis of a single crack

图12对比了不切割网格与切割网格时的位移-载荷曲线，二者几乎完全重合。结合图11、图12 可知，由X-FEM造成的网格切割不影响相场结果。此时，可安全无虞地在清晰的断裂面上引入接触、摩擦等算法。值得注意的是，使用X-FEM切割网格后，位于破坏区域的单元的长宽比得到了改善。

图12 裂纹扩展问题的位移-载荷曲线Fig.12 Load-displacement curves of single edge-notched tension test

5 结 论

提出了一种能够捕捉二维断裂力学问题相场等高线中线的算法。通过引入扩展有限元方法，使用相场等高线的中线切割网格，从而创建了清晰的裂纹界面。本文算法使得在断裂面上添加物理现象成为可能，可以缓解裂纹附近区的域网格畸变，且改善了矩阵的病态程度。

本文算法的基础是计算相场等高线与辅助网格的交点，与材料本构无关。因此，虽然本文中算例皆使用各项同性材料，但本方法亦适用于各向异性材料的情况。注意，欲使本算法成功运行，辅助网格单元的尺寸须足够大。一般地，辅助网格单元尺寸应至少为相场等高线宽度的2倍。使用时，还应尽量避免裂纹在辅助单元内部极度弯曲的场景，因为此时程序生成的相场中线线段可能部分位于相场等高线外部。数值算例表明，本文提出的中线生成算法可以成功捕捉到脆性材料典型断裂形貌的相场中线，且使用相场中线切割网格不会对相场本身产生影响。