高速角接触轴承保持架结构特性的数值模拟

刘冰洋，谢兴会，范 强，赵春江，陈 明，张晋峰，张祥云

(1.太原科技大学 机械工程学院，太原 030024；2.洛阳LYC轴承有限公司，河南 洛阳 471039;3.航空精密轴承国家重点实验室，河南 洛阳 471039)

近些年来我国航空航天工程不断发展，角接触轴承作为用于航空航天工业的关键性零部件，其在工作过程中的运动平稳性越来越引起行业学者的重视。作为高速角接触轴承的重要结构部件，保持架在动态运转过程中，其几何结构、受力情况和运动关系都极其复杂；不合理的轴承结构参数将会影响保持架的运动特性与共振特性。因此，对变结构参数下高速角接触轴承保持架的动态特性和共振特性研究就显得尤为重要。

国内外学者已经对保持架的运动特性问题做了大量研究，Walter等学者建立了处于六个自由度下的球轴承保持架的运动方程，并结合数值仿真研究了保持架在动态条件下的运动规律[1]。Gupta全面的分析了影响保持架运转平稳性的因素，并分析了不同保持架间隙比下的质心运动轨迹[2-6]。张成铁分析了轴承元件间的相互作用和角接触轴承的有关动力学特性[7]。邓四二等人通过数值方法分析了角接触球轴承保持架的动态性能[8]。杨海生在轴承动力学基础上建立了高速运转的圆柱滚子轴承保持架动力学仿真[9]。汪杨等学者研究了轴向载荷对高速角接触球轴承运动特性的影响，比较了轴承不同的运行工况条件对滚动体的位移，保持架自转角速度和位移的影响规律[10]。叶振环等分析了轴承不同的内外圈转动方式对角接触球轴承动力学性能的影响特点以及椭圆型兜孔对高速球轴承保持架动态性能的影响[11-12]。汤鹏等人研究了轴向载荷，径向载荷，转速，沟曲率系数等参数对角接触球轴承的保持架运转稳定性的影响规律[13]。张涛等学者研制了内外圈反向旋转的轴承保持架动态特性试验机并利用此试验机进行了试验分析[14]。李厅等学者对高速转动条件下的塑料型保持架进行了模态分析[15]。张文虎等学者分析了不同的轴承运行状态和不同的轴承结构参数对高速运转下的圆柱滚子型轴承振动特征的影响规律[16]。Liu Yuqing等学者在动力学基础上建立了滚动轴承滑移模型，研究了轴承所受的径向载荷，保持架连接刚度和轴承内圈加速度对轴承打滑的影响[17]。Fang B等人研究了轴承所受外部载荷，以及转速和轴承的内部游隙对球轴承刚度的影响[18]。

以上学者们主要研究了高速角接触轴承的各部件之间的接触、运动和摩擦、磨损特性。为高速角接触球轴承的研究奠定了基础。保持架结构参数变化主要包含兜孔间隙与引导间隙的变化，以及由于滚动体个数的变化引起的保持架结构参数变化。本文主要研究了定引导间隙下，变滚动体个数和变兜孔间隙对保持架运动特性和振动特性的影响，为高速角接触轴承的优化与设计提供了参考。

1 理论分析

1.1 保持架运动特性分析

保持架的旋转运动波动情况可以利用质心涡动速度偏差比来反映。通常采用保持架质心的各个瞬时径向旋转线速度的标准偏差值与保持架质心平均旋转线速度的比值来定义保持架的质心涡动速度偏差比。质心涡动速度偏差比数值越小，保持架在径向方向的波动就越小。其计算公式为：

(1)

1.2 模态分析理论

模态振动分析是动力学分析的基础，其可以反映一个机构的固有振动特性。通过分析轴承保持架的固有频率与模态振型，可以预测出保持架在实际运转工况下的振动情况，进而避免保持架发生共振。通常，对于具有n个自由度的线性系统，其振动方程可以表示为:

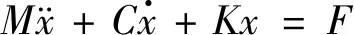
(2)

式中M为系统的质量矩阵，C为系统的阻尼矩阵，K为系统的刚度矩阵，F为系统所受的外部载荷。当系统没有阻尼和外部载荷时，振动系统的方程可以表示为：

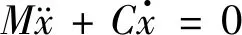
(3)

位移向量：

x=φicosωit

(4)

式中φi为模态向量，ωi为系统的第i阶固有频率；将(4)式代入(3)式可以求得特征方程，令特征方程的值为0可以得到：

(5)

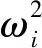
2 有限元建模

以 7218B角接触球轴承为研究对象，7218B型轴承基本结构参数见表1，具体建模过程如下:

表1 7218B轴承基本参数Tab.1 Basic parameters of 7218B bearing

首先，根据7218B轴承的结构参数，在三维制图软件SolidWorks中建立轴承的三维模型。接下来将7218B轴承的三维模型导入ABAQUS软件中。在ABAQUS中建立保持架、内圈、外圈、滚动体、引导表面、载荷加载面共计40个表面。建立滚动体与内外圈滚道、滚动体与保持架兜孔、保持架与内外圈引导面之间的相互作用共计50个。接触类型选择面与面接触，接触属性中切向接触选用罚函数，滚动体和轴承内外圈摩擦系数设为0.05，其他接触部位摩擦系数设置为0.1.有限滑移方式，接触面法向设为硬接触，接触后允许分离。径向载荷设置为2 000 N，轴向载荷设置为10 000 N.

由于轴承的结构复杂，直接进行网格划分无法实现，因此选择对轴承的各部分先进行拆分，然后再划分各部分的网格。采用扫掠的六面体网格划分方式对滚动体、内圈和外圈进行划分，在划分过程中对轴承的内圈和外圈的滚道进行局部细化，指派单元类型为C3D8R.由于保持架具有复杂的结构，因此采用以六面体为主的网格划分方式，并对保持架的兜孔区域网格进行局部细化。轴承有限元网格模型如图1所示，共有412 783个结点，322 506个单元。最后在ABAQUS的属性单元中设置轴承的内圈、外圈、滚动体和保持架的材料密度以及弹性模量和泊松比，不考虑材料的塑性变形和非线性。轴承的内外圈材料为轴承钢，尼龙为保持架的材料，氮化硅是滚动体的材料，材料参数如表2所示。

表2 材料参数Tab.2 Material parameters

图1 有限元模型Fig.1 Finite element model

3 计算与分析

3.1 动力学分析

3.1.1 滚动体个数对保持架动态特性的影响

当轴向载荷Fa=10 000 N，径向载荷Fr=2 000 N，外圈转速n=15 000 r/min(内圈固定)，兜孔间隙为1.77 mm时，将滚动体个数分别设为13、14、15、16，分别得到保持架的角速度变化曲线和质心速度偏差比如图2、图3所示。

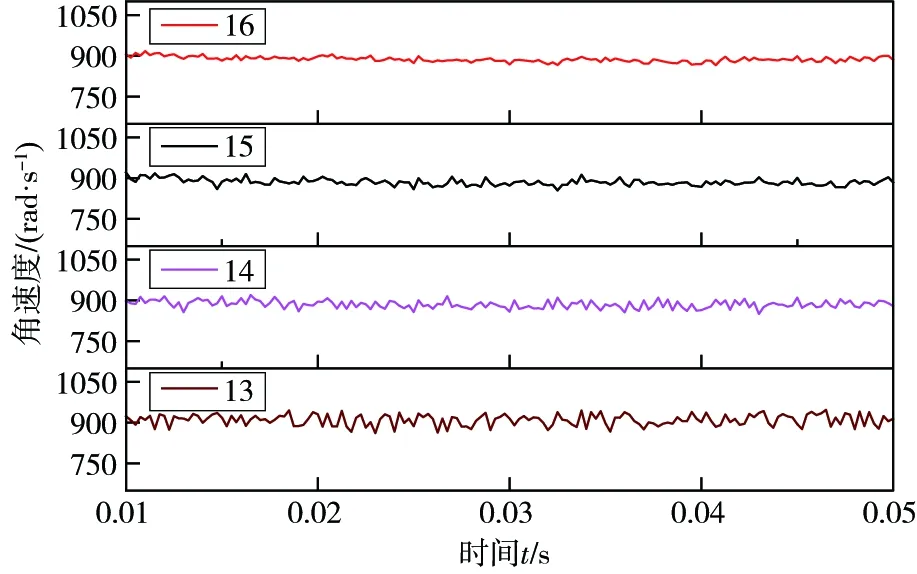
图2 不同滚动体个数下保持架的角速度变化曲线Fig.2 The angular velocity change curve of cage under different number of rolling elements

图3 不同滚珠个数下保持架质心涡动速度偏差比Fig.3 Deviation ratio of cage centroid vortex velocity under different number of balls

由图2和图3可以看出，当滚动体个数逐渐增加时，保持架的角速度波动幅度逐渐变小，质心涡动速度偏差比呈下降趋势。这是因为在其它条件不变的情况下，当滚动体个数增加时，每个滚动体承受的载荷减小，滚动体与保持架的碰撞力变小，摩擦力也减小，从而使质心运动趋向稳定。因此在滚动轴承设计中，适当的增加滚动体的数目，可以减少保持架的波动情况。

3.1.2 兜孔间隙对保持架动态特性的影响

当轴向载荷Fa=10 000 N，径向载荷Fr=2 000 N，外圈转速n=15 000 r/min(内圈固定)，滚动体个数为16，兜孔间隙分别为0.42 mm、0.87 mm、1.32 mm、1.77 mm时。分别得到保持架的角速度变化曲线和质心速度偏差比如图4、图5所示。

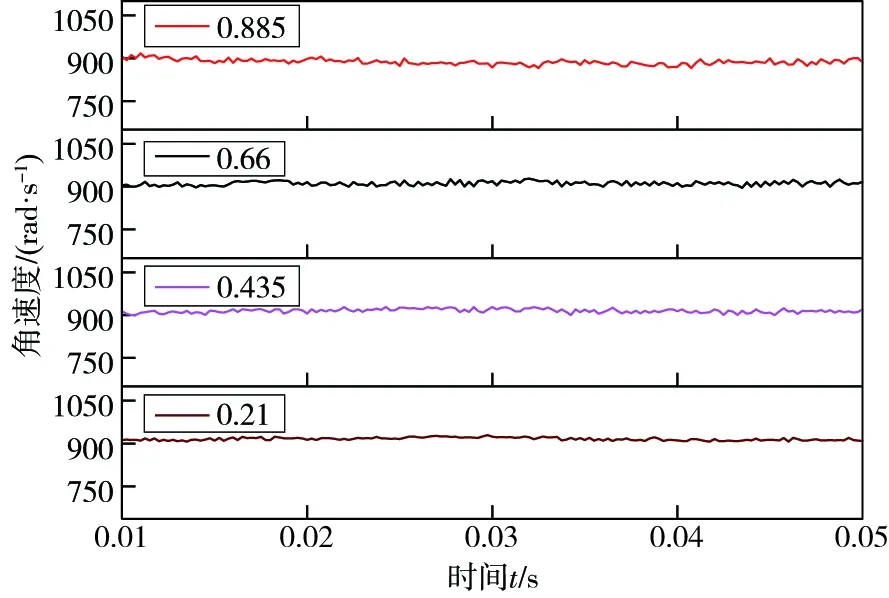
图4 不同兜孔间隙下保持架的角速度变化曲线Fig.4 Change curve of angular velocity of cage in different pocket gaps

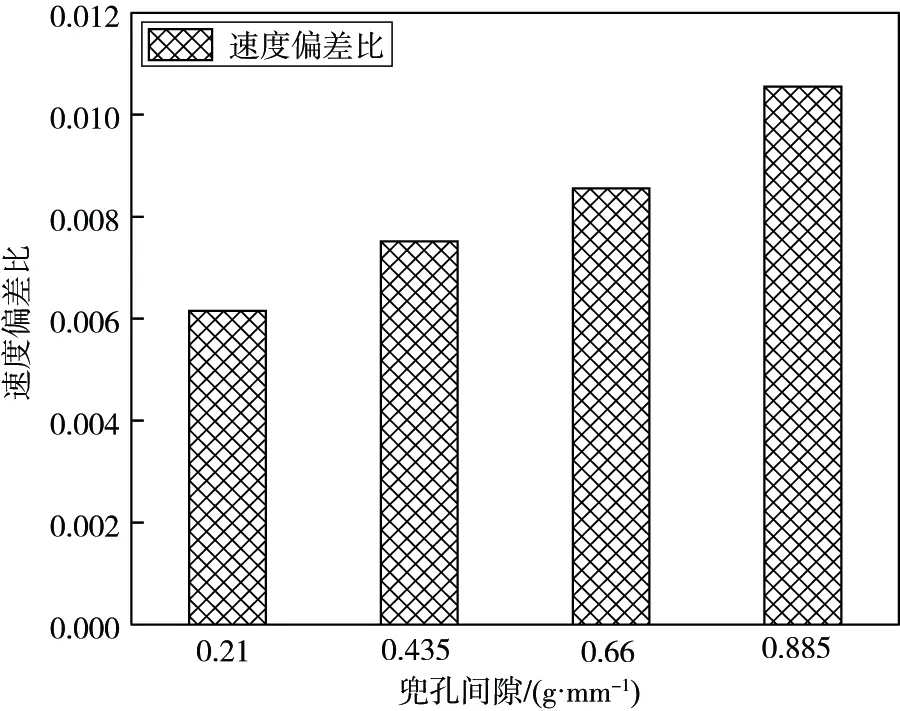
图5 不同兜孔间隙下保持架质心涡动速度偏差比Fig.5 Vortex velocity deviation ratio of the center of mass of the cage under different pocket gaps

从图4和图5可以发现，增大保持架兜孔的间隙，会使保持架的质心涡动速度偏差比小范围变大，从整体来说，质心涡动速度偏差比都具有较小的数值，保持架具有较好的运转平稳性。因此，通过减小兜孔间隙的办法来提高保持架的运转平稳性，效果并不显著；并且兜孔间隙减小将会增大滚动体和保持架之间的碰撞风险，加剧保持架和滚动体之间的磨擦，不利于轴承内部之间的润滑，造成滚动体或者保持架的过早失效。

3.2 模态分析

把7218B轴承保持架的实体三维模型导入到ABAQUS有限元软件中，分别设置保持架的材料类型与属性类型。再进行分析步与历史输出变量的设置，选择50作为特征值求解的个数。由于角接触轴承保持架的结构形式复杂，在进行网格划分时，为了获得较高的计算精度，除仍采用六面体网格划分外，需要对保持架的兜孔处的网格进行局部细化。图6为保持架的有限元网格模型。最后，借助ABAQUS软件里的求解器Lanczos进行求解。

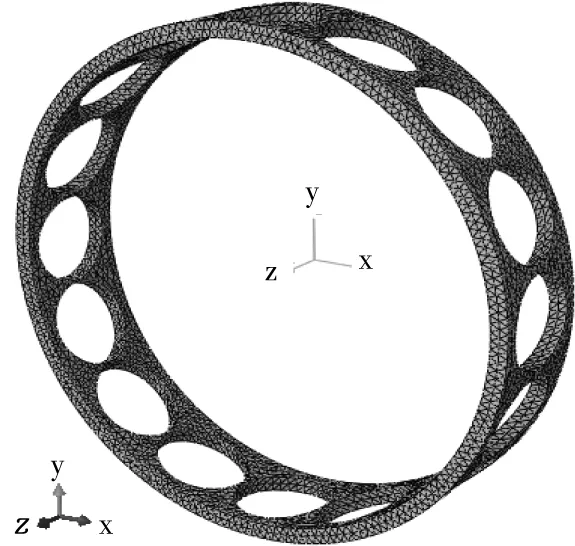
图6 保持架网格模型Fig.6 Mesh model of the cage

3.2.1 不同滚动体个数对保持架模态的影响

由图7可知，随着滚动体的个数的增多，保持架的各阶固有频率逐渐减小。从图8来看，保持架的振动主要包括以下两个方面，即保持架内外表面的弯曲变形和面外扭转变形，由于保持架的扭转变形，因此，当外加激励的频率和保持架的固有频率相等时，将激发共振。因此，随着滚动体数目的增加，保持架的共振风险将加大。

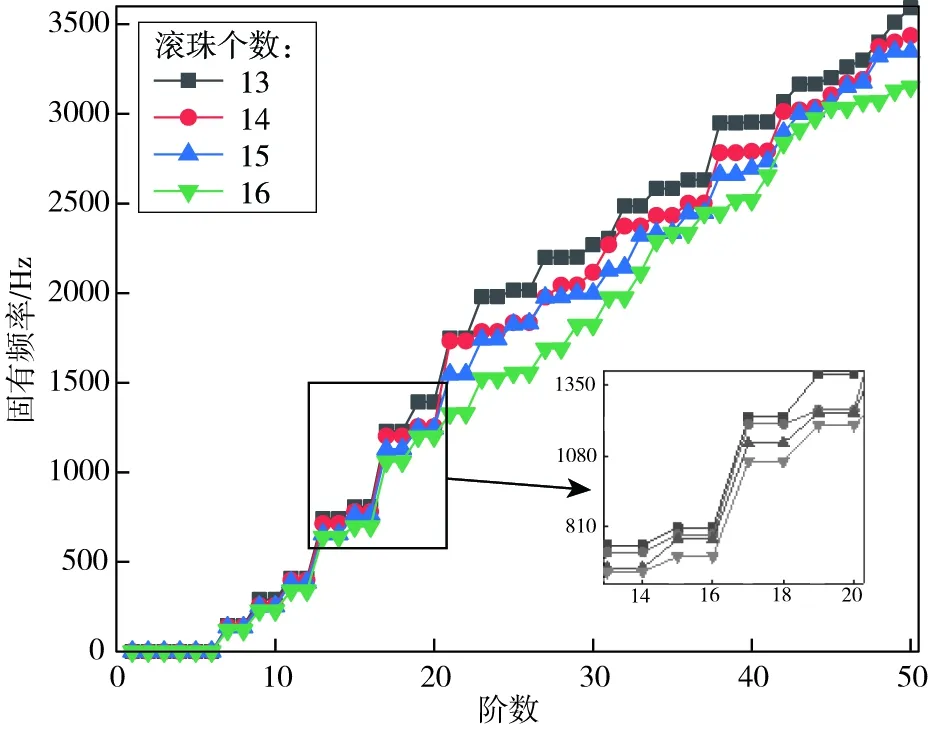
图7 不同滚动体个数下保持架固有频率变化曲线Fig.7 The natural frequency change curve of the cage with different ball numbers

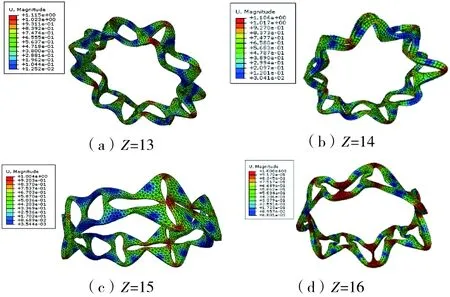
图8 不同滚动体个数下保持架第50阶模态振型图Fig.8 50th modal shape diagram of cage with different number of balls

3.2.2 不同兜孔间隙对保持架模态的影响

从图9中可以看出，保持架的每一阶固有振动频率均随着保持架兜孔间隙值的增大而减小，显然这增大了保持架发生共振的风险。图10为不同的兜孔间隙对应的保持架第50阶模态振型，保持架变形量最显著的部位发生在兜孔与兜孔连接的部位。这将为保持架的结构设计提供有益参考。

图9 不同兜孔间隙下保持架固有频率变化曲线Fig.9 The natural frequency change curve of the cage with different pocket gaps

图10 不同兜孔间隙下保持架的第50阶模态振型Fig.10 50th modal shape diagram of cage with different pocket gaps

4 结论

为提高轴承保持架运转的平稳性，本文利用ABAQUS有限元分析软件建立了在轴承外圈引导时7218B型轴承的多体动力学模型，研究了不同的滚动体数目以及不同的兜孔间隙对保持架的运转平稳性及模态振动特性的影响，得到以下结论：

(1)随着滚动体个数的增加，保持架的角速度波动幅度逐渐变小，质心涡动速度偏差比呈下降趋势，保持架的运转平稳性得到增强，但较多的滚动体个数使得保持架的各阶固有频率有所降低，保持架共振的风险增大。

(2)随着保持架兜孔间隙逐渐变大，保持架的角速度波动幅度处于较低的水平；虽然质心的涡动速度偏差比值有所变大，但是从整体范围上看，质心的涡动速度偏差比的数值始终维持在较低的水平。并且，随着兜孔间隙的增加，保持架的各阶固有频率均降低，增大了保持架共振的风险。