一种基于时间序列与核岭回归的结构损伤定位方法

何定桥,杨 军

(清华大学 土木工程安全与耐久教育部重点实验室,北京 100084)

0 引言

近年来,随着计算机技术、传感器技术的快速发展,结构健康监测逐渐成为研究热点,结构健康监测的一个重要目的是结构损伤识别与定位[1-2]。结构损伤识别与定位由以下部分构成:(1) 判别结构是否存在损伤;(2) 判别结构损伤发生的位置;(3) 判定结构的破坏程度;(4) 对结构健康状况进行评估。其中,对结构损伤位置及损伤程度的判断是难点。基于上述(2)、(3)部分可以实现结构状况的整体评价。通过无线智能传感器配合云平台可以实现建筑结构的全天候不间断监测。在地震荷载、风荷载等作用下结构出现损伤时,监测数据可以有效反映结构的损伤信息[3-4]。

基于监测数据的结构损伤识别与定位可分为模态参数方法和非模态参数方法。模态参数法是根据结构模态参数在损伤前后的变化反映结构损伤的信息。常见的模态参数包括固有频率[5]、模态振型[6]、振型曲率[7]及应变曲率模态曲率[8]等。基于模态参数的方法因对损伤不敏感、模态振型测量复杂、容易受外界干扰等问题,在实际工程应用中受到很大的限制,实用性还需进一步的研究[9]。非模态参数法原理是对结构振动响应进行变换后得到可以反映结构损伤的参数来进行损伤识别与定位。非模态参数法包括基于小波变换[10-12]、希尔伯特黄变换[13]、时间序列等模型方法。时间序列模型最初应用于经济学和电气工程领域,后在结构监测领域被大量应用。Fugate 等[14]建立了结构的自回归模型,提取模型残差作为损伤特征量,采用质量控制图法监测结构状态。H.Sohn等[15]建立了自回归-外加输入自回归模型(AR-ARX),以模型残差作为特征量,采用统计模式识别方法进行损伤识别与定位。刘毅等[12]建立了自回归滑动平均模型(ARMA),基于自回归部分参数,采用主成分分析法提出结构损伤特征指标。然后采用t-检验考察该指标在损伤前后的变化进行损伤定位。王真等[16]建立了自回归系数的损伤灵敏度矩阵,通过该矩阵反映的自回归系数变化与损伤系数变化之间的关系进行损伤识别与定位。

卢宏彬[17]基于ARMA模型构造了残差指标、前三阶指标和马氏距离指标在内的损伤指标体系对结构损伤进行了识别,并将该方法应用于主跨428 m的广州新光大桥健康监测系统上。杜永峰等[18]建立了AR模型,将待识别工况的残差与AR预测参考模型的残差的方差之比作为损伤指标。张凯玮等[19]基于ARMA模型和马氏距离定义了损伤指标,根据各工况下隧道结构的加速度响应进行了损伤识别分析,实现对盾构隧道结构损伤的检测和定位。

可见,当前基于ARMA模型的结构损伤识别研究普遍利用自回归系数的统计学特征,理论意义不明确,主观性较强。而核岭回归算法具有非线性、拟合性能强、泛化能力强等特点。本文结合ARMA时间序列模型与核岭回归提出了一种结构损伤识别与定位的新方法,并用算例验证了其有效性。

1 理论基础

结构损伤会改变结构的动力特性,也会改变结构在时域响应的统计特性[20]。时间序列模型可以将大量结构响应数据所蕴含的信息凝聚为少量的模型参数,例如自回归系数、滑动平均系数和模型残差方差等,其中的自回归系数内含了结构的固有动力特性,可以通过机器学习算法建立结构自回归系数变化与损伤的联系,进行损伤识别与定位。

1.1 ARMA模型的建立

对于一个平稳、正态、零均值的时间序列{Xt},若xt与前p步取值xt-1,xt-2,…xt-p,前q步输入激励at-1,at-2,…at-q有关,则时间序列模型可以表示为:

(1)

式中:p是自回归模型的阶数;q是滑动平均模型的阶数,模型记为ARMA(p,q)，φ和θ分别是时间序列和输入激励的各阶特定系数。对式(1)引入后移算子B,使得Bixt=xt-i,模型可以表示为:

(2)

(3)

上式反映了系统的脉冲响应函数,分子θ(B)包含了结构与外部之间的交换关系,分母φ(B)包含了结构的固有特性信息。利用结构在外界激励下的位移/加速度时程建立ARMA模型,模型的自回归系数包含了结构固有特性信息。

1.2 自回归系数与结构损伤的联系

对于发生损伤的结构,其总体刚度矩阵为:

(4)

式中：ki为第i个构件未发生损伤时的刚度矩阵；M为构件的数量；定义αi为第i个构件的损伤系数,αi∈[0,1],未发生损伤时αi=0,完全损伤时αi=1。

结构发生损伤后,模态参数会发生变化,反映结构固有特性信息的自回归系数会发生变化,但是自回归系数的变化与结构损伤系数αi不一定是线性变化的。假设结构有p个测点,对每个测点信号可以提取前q阶自回归系数,共可获得s=p×q个自回归系数。定义自回归系数向量为:

{φ}=[φ1,φ2…φs]T

(5)

对自回归系数φi(i∈[1,s])做一阶变分:

(6)

自回归系数向量的一阶变分可以表示为:

{δφ}=[δφ1,δφ2,…δφs]T=

(7)

式中:P为s行、M列矩阵;Pij反映了损伤系数αj的单位变化引起第i个自回归系数的变化量(i∈[1,s],j∈[1,M])。

自回归系数的一阶变分反映了损伤结构自回归系数与未损伤结构的自回归系数之差:

(8)

(9)

可以得到:

{δφ}={φ}-{φ0}=P{δα}=P{α}

(10)

进而求出结构损伤系数向量{α}:

{α}=P+[{φ}-{φ0}]

(11)

式中:P+为P的伪逆矩阵,定义为损伤识别矩阵。该矩阵只与结构自身的动力特性有关,若能求出P+矩阵,便可以乘上损伤结构与未损伤结构的自回归系数向量之差求出结构的损伤系数向量,从而识别损伤的位置与大小。

1.3 利用核岭回归获得损伤识别矩阵

有大量的损伤样本与对应的自回归系数时,可以通过机器学习(Machine Learning)对损伤识别矩阵进行估计。自1950年图灵提出机器学习的概念以来,其理论和方法发展迅速,在土木工程的多个细分领域已被广泛应用[21-22],对损伤程度的预测适用于连续型有监督的回归算法(Regression),首先考虑使用普通的线性回归对结构损伤系数进行回归预测:

(12)

(13)

式中：N是训练集中的样本数量。其使用最小二乘法求得的解为:

(14)

求解线性回归的前提条件是对给定数据集X,XTX可逆。结构监测系统存在多个测点,每个测点获得的自回归系数阶数较高,样本的特征数量s较高,部分特征之间可能高度相关,则XTX接近于奇异的病态矩阵。上述问题变为不适定问题,计算误差很大,在最小化目标中加一个惩罚项,使得目标函数变为:

(15)

这种回归称为岭回归(Ridge Regression)。岭回归可以限制模型的复杂度,防止过拟合(Overfitting),使得模型在复杂度和性能间达到平衡,可以有效应用于结构损伤定位。λ是待定的参数,岭回归的关键是找到合理的λ来平衡模型的损失函数和偏差。使用岭回归求得系数的解为:

(16)

(17)

这种回归称为核岭回归,目标函数可以表示为:

(18)

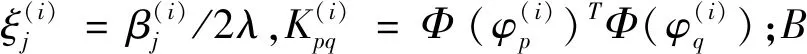
K(x(i),x(j))=Φ(x(i))·Φ(x(j))=

(19)

2 数值算例

利用时间序列与核岭回归进行结构损伤识别与定位,需建立有限元模型,在模型中模拟结构的损伤。假设结构有p层,识别精度仅限于损伤发生的楼层,损伤模式记为{α}=[α1,α2,…,αp],共随机生成m种破坏模式。

对m个损伤模型分别输入环境激励,每个模型输出p条响应。对每条输出响应均建立ARMA模型,每个ARMA模型提取前q个自回归系数,得到s=p×q个自回归系数作为后续核岭回归输入特征,自回归系数记为{φ}=[φ1,φ2…φs]T。

将每种损伤模式的s个自回归系数作为核岭回归的输入特征,损伤系数作为输出变量,对模型进行训练。完成训练的模型可以接受结构发生未知损伤后提取的自回归系数,输出预测的损伤系数。

2.1 有限元模型

本文采用4层钢筋混凝土框架结构作为数值算例,该结构长3.0 m、宽2.0 m、层高2.6 m,梁均为高0.66 m、宽0.25 m的矩形梁,柱为0.4 m×0.6 m矩形截面柱,采用开源有限元软件OpenSees建立结构有限元模型。该模型采用线弹性模型,楼面荷载3 kN/m2,混凝土采用C30,弹性模量为3×104MPa。模型如图1所示。

图1 混凝土框架OpenSees有限元模型Fig.1 OpenSees FEM model of the concrete frame

沿结构短边方向(Y向)在底部输入白噪声激励,激励时长30 s,采样间隔为0.01 s,采样频率为100 Hz。未损伤结构在白噪声激励下一层(图1中A点)及4层(图1中D点)加速度时程如图2所示。

图2 混凝土框架白噪声激励下加速度时程Fig.2 Acceleration time history of concrete frame under white noise excitation

2.2 特征提取

对受损伤的结构输入白噪声后得到4层加速度时程(图1中A,B,C,D点),分别建立ARMA模型,该模型要求输入的时间序列是平稳的,且首先对时间序列的稳定性进行单位根检验(ADF),然后对模型进行定阶。

选择合适的模型阶数非常重要,模型的阶数越大拟合性越强,但阶数过高误差会加大,造成过拟合[23]。常用的定阶方法包括自相关系数法、偏相关系数法、赤池信息量准则法(AIC)及贝叶斯信息准则(BIC)等。本文对模型采用AIC热力图定阶,根据经验取AR阶数1～30,MA阶数1～5,分别计算对应的ARMA模型的AIC,选取使得AIC最小的AR与MA阶数组合。

如图3所示为未损伤结构4层加速度时程ARMA模型的AIC热力图。随着AR与MA阶数的增大,AIC基本稳定于2.6。模型的AR与MA阶数可选择(19,1)、(14,2)、(12,3)、(12,4)、(9,5)等组合,实际计算过程中优先选择MA阶数较小的模型(19,1)。

图3 ARMA模型AIC定阶热力图Fig.3 AIC heatmap of ARMA model

为保证输入信息的完整性,核岭回归模型取每条信号ARMA模型的前10阶自回归系数,损伤系数为柱刚度折减系数。对于第三层柱刚度折减30%的损伤模型(α1= 0,α2=0,α3=30%,α4=0)自回归系数分布如图4所示。图5中可以看到结构受到损伤后自回归系数系数发生了显著改变,且不同层自回归系数变化不同。

图4 损伤结构前10阶自回归系数Fig.4 Top 10 autoregressive coefficients of damaged structure

图5 损伤结构与未损伤结构前10阶自回归系数之差Fig.5 Difference between the top 10 autoregressive coeffici- ents of damaged and undamaged structures

2.3 数据集搭建与模型训练

本文通过对上述有限元模型进行随机构造损伤,共生成损伤模型1 200个,分别输入白噪声激励后得到4 800条加速度时程数据,对每条加速度时程分别建立ARMA模型,每个ARMA模型提取前10阶自回归系数,每个损伤模型对应40个自回归系数以及4个输出变量(1层、2层、3层、4层的结构损伤系数)。将数据集进行分割,随机选取1 000个损伤模型作为训练集,其余200个模型作为验证集。

机器学习中超参数选择对模型的预测精度至关重要。核岭回归中需要确定的超参数包括:(1)正则化系数λ,表征正则化的强弱,λ过小可能出现过拟合,λ过大可能使得模型回归系数太小,出现欠拟合;(2)核函数(Kernel),不同核函数泛化能力不同,平滑程度不同,适用的样本也不同,本文依据经验选取最为常见的核函数径向基函数;(3)径向基函数参数γ代表RBF的幅宽,会影响模型的泛化性能。需要确定的超参数只有λ和γ,且超参数范围已知,可以利用穷举搜索找出使得模型表现最好的超参数。

本文中对4个输出变量的预测分为4个模型,确定超参数后对模型进行训练,如图6所示,单个模型训练时长约为4～5 s,模型整体训练总时长约16～20 s。

图6 模型训练样本量与训练时间Fig.6 Model training sample size and training time

如图7所示,单层的核岭回归模型R2在训练集上可以达到一层95%、二层84%、三层81%、四层88%,在验证集上可以达到一层81%、二层67%、三层68%、四层66%。训练样本数量超过400后模型表现趋于稳定。

图7 模型R2学习曲线(R2小于0时,图中体现为0)Fig.7 Model R2 learning curves

为了验证核岭回归的优势,使用无正则化无核函数的线性回归(Liner Regression)、有正则化无核函数的岭回归(Ridge Regression)、无正则化有核函数的支持向量回归(Support Vector Regression)三种算法与其进行对比。

如图8、图9所示,在训练集上,线性回归表现最好,R2在训练过程中维持在95%以上,均方误差(MSE)维持在0.001以上,但在验证集上线性回归表现很差,R2维持在0及0以下,模型出现过拟合。

图8 不同回归算法模型R2学习曲线 (R2小于0时,图中体现为0)Fig.8 Model R2 learning curves with different regression methods

图9 不同回归算法模型MSE曲线Fig.9 Model MSE curves with different regression methods

表1为最终几种回归模型的表现,岭回归、支持向量回归的表现介于线性回归与核岭回归之间,结果说明添加正则化与核函数后可以显著提升模型的拟合性能与泛化性能。

表1 不同回归模型训练时间及表现对比Table 1 Training time and performance of different regression models

2.4 模型验证与应用

为验证模型损伤识别与定位的准确性,选取5种工况进行验证,分别为未受损工况、两种单损伤工况(结构仅一处发生损伤)及两种多损伤工况(结构多处发生损伤)。损伤情况如表2所列。

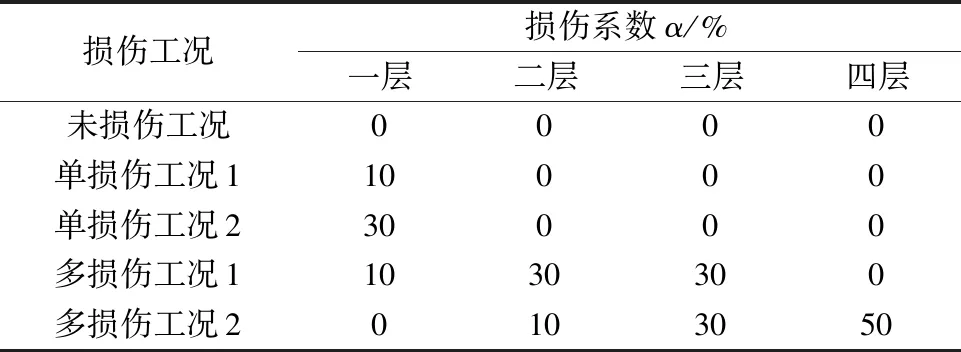
表2 模型损伤工况Table 2 Damage conditions for model

对未受损的原结构,核岭回归模型识别一至四层的损伤系数分别为4.6%、0.4%、3.2%、4.2%,平均误差为3.1%；对于单损伤工况1,一层损伤10%,模型识别一层的损伤为8.9%,一至四层平均识别误差为2.7%;对于单损伤工况2,一层损伤30%,模型识别一层的损伤为29.0%,一至四层平均识别误差2.7%;对于多损伤工况1,模型一层、二层、三层发生10%、30%、30%损伤,模型识别结果为10.1%、28.9%、24.3%,一至四层平均识别误差2.7%;对于多损伤模型2,模型二层、三层、四层发生10%、30%、50%损伤,模型识别结果为9.3%、30.6%、55.2%,一至四层平均识别误差3.3%。由表2可看出，模型在多种工况下均表现出较高的识别准确率。损伤识别完整结果列于表3。

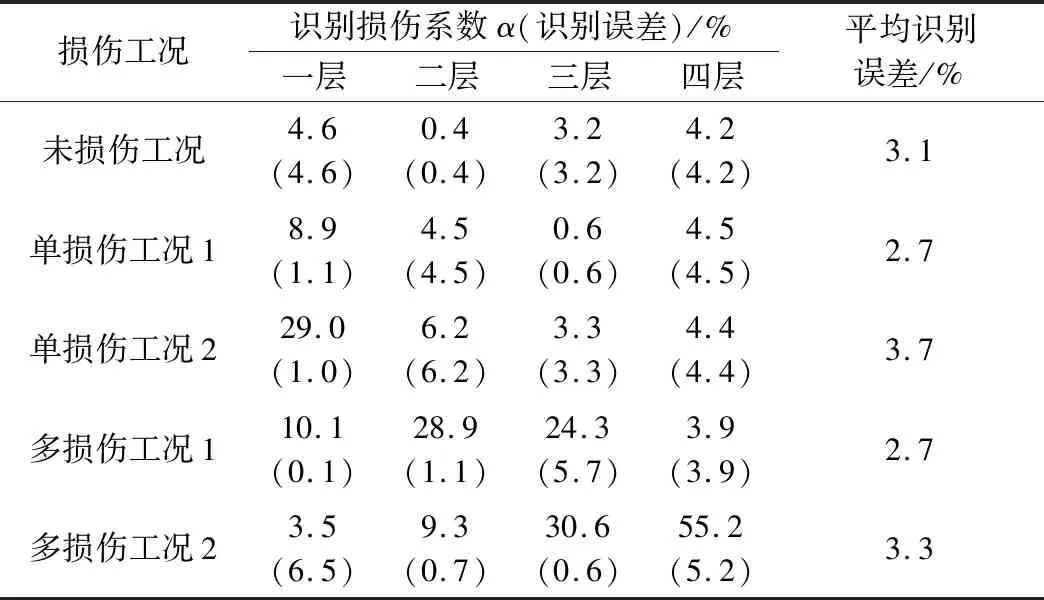
表3 损伤识别结果Table 3 Damage identification results

3 结论

本文通过理论分析并结合数值模拟,建立了核岭回归模型,利用结构时间序列模型中自回归系数实现了结构损伤识别与定位:

(1) 提出结构的损伤识别矩阵P+,该矩阵只与结构自身的动力特性有关,若能求出该矩阵便可以通过损伤结构与未损伤结构的自回归系数向量之差识别结构的损伤位置与大小。

(2) 通过4层框架结构数值模型对理论进行验证,模型R2在训练集上可以达到80%,在验证集上可以达到65%。对多个单损伤和多损伤工况进行验证,模型识别平均误差不超过3.7%。

(3) 相比无正则化无核函数的线性回归、有正则化无核函数的岭回归、无正则化有核函数的支持向量回归三种算法,核岭回归准确率最高,说明核函数和正则化可以有效提高模型的拟合性能与泛化性能,更好地应用于结构损伤识别。

本文不足之处在于需要建立结构较为精确的有限元模型,且需对结构各种损伤下的情况进行数值模拟,建立ARMA模型,需要较高的计算成本。