两部定价契约下基于销售努力的双渠道供应链定价与协调
黄红伟,陈振颂,吴 胜,焦建锋,王先甲
(1.郑州航空工业管理学院 数学学院,河南 郑州 450046;2.武汉大学 土木建筑工程学院,湖北 武汉 430072;3.河南财经政法大学 电子商务与物流管理学院,河南 郑州 450016;4.武汉大学 经济与管理学院,湖北 武汉 430072)
0 引言
2020年突如其来的新冠肺炎疫情,让中国的零售业出现了“冰火两重天”的局面:传统渠道销量惨淡,电子渠道则乘势而起,迅速发展。传统零售商面临着市场份额逐渐被电子渠道蚕食的危机,鉴于此,传统零售商纷纷采用各种策略提高顾客线下购物满意度,增加产品市场需求量,以期在激烈的竞争环境中获得较多的利润。销售努力作为提高顾客满意度,增加其市场份额的一种重要手段,被广大零售商所采用。例如百货超市每隔一段时间调整各种商品的陈列摆放位置和形状,通过导购、宣传等增加消费者对产品功能、质量的了解,通过不同的店面装修、企业文化增加消费者的购物兴趣,这些销售努力从视觉、听觉和感觉等多方面增加了消费者的购物体验,从而引导产品市场需求的变化。传统零售商的销售努力是其增加产品市场需求量、抢占市场份额的关键手段,特别是在新冠疫情对传统零售业带来不利影响的前提下,更需要传统零售商重视销售努力,提高销售努力水平。因此在电商平台参与下(电商平台扣点费率[1]固定),研究不同决策模式下基于销售努力的双渠道供应链最优定价决策问题具有重要的实践意义。
近年来,在双渠道供应链定价决策的研究中,ZHOU等[2]研究了信息不对称下垄断制造商和零售商在双渠道供应下的定价决策,并研究了信息不对称对供应链定价决策的影响。考虑价格和交货时间对双渠道供应链的影响,MODAK等[3]从线下和线上渠道的零售价格、订货量,以及线上渠道的交货时间等方面对双渠道供应链定价决策进行了研究。WANG等[4]研究了由两个制造商和一个零售商组成的三元供应链,两个制造商通过电子渠道和传统渠道销售互补性产品的双渠道定价和服务决策问题。毛照昉等[5]考虑线下零售商为线上零售商提供售后服务的双渠道营销定价决策问题,对比分析了分散决策和集中决策下供应链的最优定价策略。刘广东等[6]利用Stackelberg博弈理论探究了生产成本扰动和风险规避对双渠道供应链定价和订购决策的影响。可以发现,关于双渠道供应链定价决策的研究主要聚焦在考虑信息、交货时间、售后服务等不同因素对决策的影响,然而考虑电商平台扣点费率下传统零售商的销售努力对双渠道供应链定价决策影响的研究则相对较少。面对新冠肺炎带来的线下销售困境,本文从传统零售商销售努力视角出发,基于电商平台扣点费率,研究销售努力对供应链最优定价决策以及供应链整体利润的影响。
销售努力对供应链定价决策的影响主要体现在销售努力引导消费者购买意愿,增加产品市场需求等方面。现有研究主要从不同方面展开:TAYLOR[7]研究了销售努力影响渠道回购策略下的供应链协调问题,结果表明在销售努力影响产品市场需求的前提下,单一线性回购契约不能实现供应链的协调。SAHA等[8]考虑产品市场需求受价格和销售努力水平的影响,研究了由制造商、分销商和零售商组成的三级供应链渠道协调问题。RANJAN等[9]考虑产品市场需求受到绿色度和销售努力水平的影响,基于收益共享契约研究了双渠道供应链的定价策略和协调机制。MA等[10]研究了3种均衡策略下生产商和零售商同时进行销售努力对供应链定价决策和最优利润的影响。姚锋敏等[11]则研究了零售商和制造商分别进行销售努力的情形下,考虑企业社会责任行为的闭环供应链定价决策问题。相对于上述笼统的销售努力,展厅作为销售努力的一种具体形式,亦得到了国内外学者的广泛研究。LI等[12]研究了展厅对双渠道供应链最优定价决策和服务努力的影响,考虑无服务、事前服务和事后服务等情形,研究结果显示展厅效应使企业在事后服务情形下的收益最大;刘灿等[13]认为零售商线下展厅效应对制造商线上渠道需求具有促进作用,构建了集中式决策与分散式决策下的双渠道供应链定价模型。
不同于上述文献中采用的批发价格契约和收益共享契约,本文研究了两部协调定价机制下基于销售努力的双渠道供应链定价决策问题,并将电商平台的扣点费率作为外生变量纳入模型考量范围;然后,分析了分散决策、集中决策和两部协调定价决策3种模式下的最优定价决策,并分析了销售努力水平和电商平台扣点费率对最优定价决策和供应链局部利润以及整体利润的影响,并得出相应的结论;最后,通过灵敏度分析,验证了相关命题,并阐述了本文研究的理论意义和现实意义。
1 模型描述与假设
本文研究由一个生产商、电商平台和一个传统零售商组成的双渠道供应链定价决策问题。在电子渠道中,生产商通过电商平台以售价pE直接向消费者销售产品,并支付给电商平台一定的销售费用δ(0<δ<1)(扣点费率[1],本文设定其为常数);在传统渠道中,制造商以批发价格w销售产品给传统零售商(线下零售商),传统零售商再以零售价格pT销售产品给消费者。具体双渠道供应链结构如图1所示。

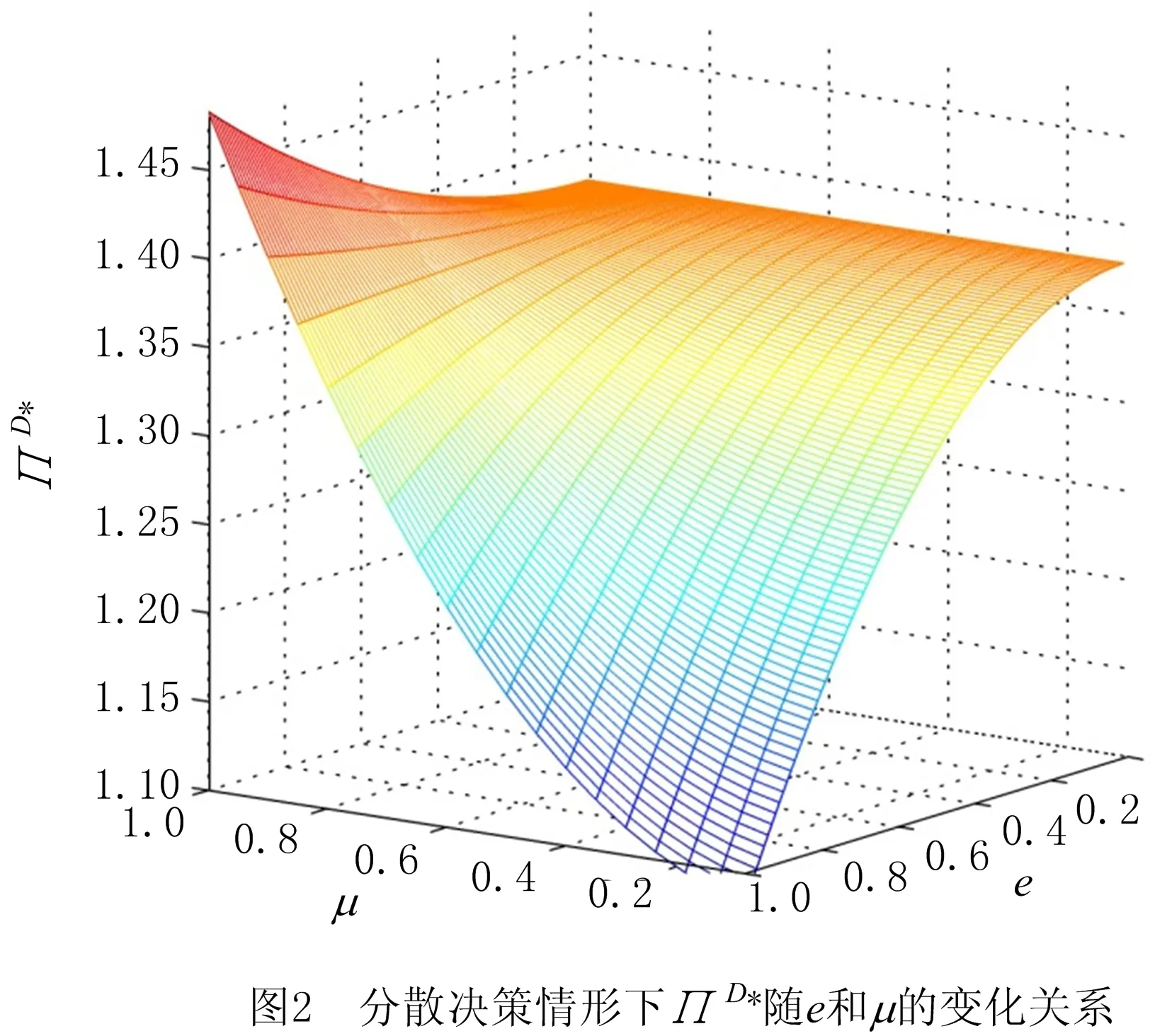
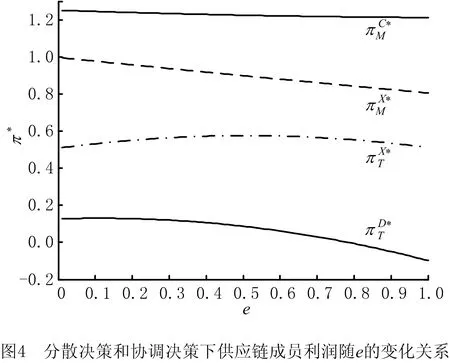
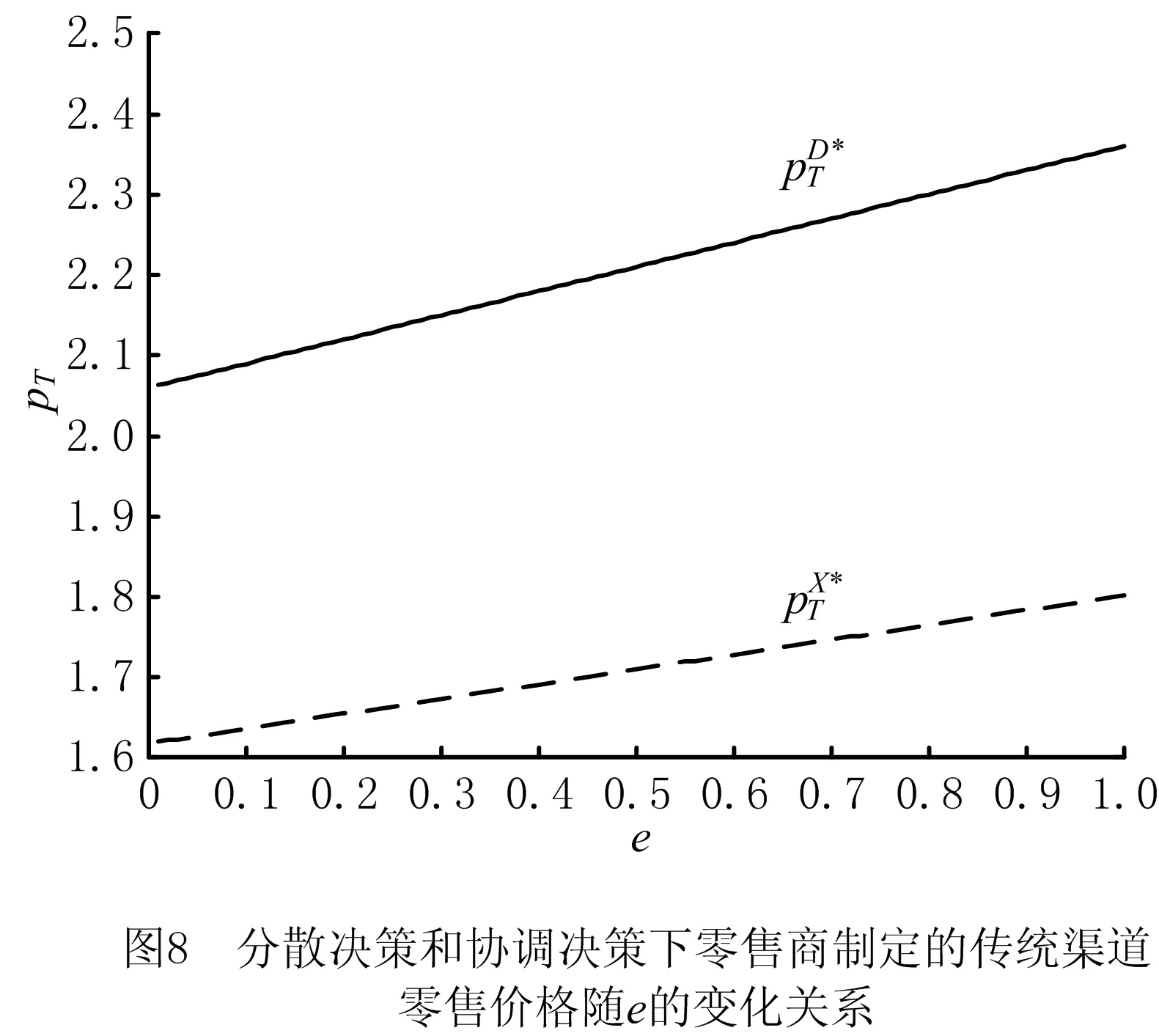
为了提高产品的销售量,传统零售商进行销售努力e(0 为了方便研究,本文给出如下假设: 假设1制造商的生产成本不予考虑,电商平台和传统零售商的销售成本不计,并且不考虑产品缺货。 假设2①制造商和传统零售商基于批发价格契约销售产品,即制造商通过批发价格w销售产品给传统零售商,传统零售商再以零售价格pT销售产品给消费者;②制造商通过电商平台以零售价格pE直接销售产品给消费者,电商平台统一收取扣点费用δ(0<δ<1),该变量为外生变量。 假设3产品市场需求受零售价格和销售努力水平两个因素影响。 考虑传统零售商进行销售努力[14]对供应链成员产品市场需求量的影响,假设产品在双渠道上的需求量为一个常数,线下零售商进行销售努力以后,线下渠道需求量的增加将导致线上渠道需求量的降低,为了简化模型,本文假设增加量和减少量相同,结合文献[14]设传统渠道和电子渠道的需求函数分别为: qT=a-kpT+ηpE+μe; (1) qE=b-kpE+ηpT-μe。 (2) 式中:a表示偏好传统购物方式的消费者的基础需求量;b表示偏好电子购物方式的消费者的基础需求量,且a,b>0;k表示消费者对产品价格的敏感系数;η表示传统渠道和电子渠道之间由于价格变化而造成的需求扩散程度,k,η均为常数,且0<η 传统零售商利润函数为: (3) 制造商的利润函数为: πM=qTw+(1-δ)pEqE。 (4) 结合文献[1],可知由生产商和传统零售商组成的双渠道供应链的利润函数为: (5) (6) (7) (8) (9) wD*=(1-δ)[(4k2-δη2)(a+eμ)+2ηk(2-δ) (b-eμ)]/[8k(1-δ)(k2-η2)-kδ2η2], (10) 使生产商利润最大化。 同时求解二阶偏导数,可得Hesse矩阵: 联合上述两式,可得最优的电子零售价格和批发价格如式(9)和式(10)所示。命题1得证。 该命题表明,在双渠道供应链中,生产商的最优策略受到电商平台收费比率的影响(现实生活中,一般电商平台的收费比率在5%~20%之间,详见文献[1])。因此,生产商可以根据相应的收费比率,确定最优的电子零售价格和批发价格。 将求解的式(9)和式(10)代入式(7)中,可得传统零售商的最优零售价格为: (b-eμ)]/[8k(1-δ)(k2-η2)-kδ2η2]。 (11) 由式(9)~式(11)可得生产商和传统零售商的最优利润函数分别为: δηk(b-eμ))2/[k(8(1-δ)(k2-η2)- (12) (a+eμ)2-ηk(a+eμ)(b-eμ)(3δ-4)]/ [8k(1-δ)(k2-η2)-kδ2η2](1-δ)。 (13) A=μ(k-η)(1-δ)(2η+2k-δη); B=2ak2-2aη2+aδη2+bδηk; C=8δη2-8δk2-8η2+8k2-δ2η2; 证明传统渠道和电子渠道的需求量、最优零售价格随销售努力水平的变化关系可由一阶偏导数直接求解获得。下面求解传统零售商的最优销售努力水平。求解传统零售商和生产商最优利润关于销售努力水平e的一阶偏导数可得: (2η+2k-δη)·[(2ak2-2aη2+aδη2+bδηk)+ eμ(2k2-2η2+δη2-δηk)]/ [k(δ2η2-8δη2+8δk2+8η2-8k2)2]; ηk(b-a)·(4-3δ)+2ak2+(2η2+6k2-8ηk- 2δη2-4δk2+6δηk)·μe]/ [k(8δη2-8δk2-8η2+8k2-δ2η2)]。 eD*=2μ(k-η)(1-δ)2(2ak2-2aη2+aδη2+ bδηk)·(2η+2k-δη)/[kξ(8δη2-8δk2-8η2+ 8k2-δ2η2)2-2μ2(k-η)2(1-δ)2 (2η+2k-δη)2]; (14) eD=k(a+b)(2δ2-9δ+8)/[2μ((3-2δ)k- η(1-δ))·(2-δ)]-δk(a+b)/[2μ(k-η) (2-δ)]-a/μ。 (15) 由命题2可知,在分散决策情形下,传统零售商提高销售努力水平,将增加消费者对传统渠道购物的好感度,从而增加其产品的市场需求量,并直接增加传统零售商的最大化利润;但是,当销售努力的水平提高到一定程度(eD*)以后,提高销售努力水平对产品需求量的增加速度小于零售价格增加对产品需求量的降低速度,即提高销售努力水平获得的利润小于提高销售努力水平产生的成本。因此,传统零售商将选择最优销售努力水平eD*来获得最大的利润。 对于生产商来说,传统零售商销售努力水平的提高,将降低消费者对电子渠道购物的好感度,造成其产品市场需求量降低,故而生产商只能通过降低电子渠道的零售价格来提高其市场需求量。因为eD* 在集中决策情形下,生产商和传统零售商作为一个整体,并基于供应链整体利润最大化进行决策,从而确定最优的传统零售价格和电子零售价格。由式(3)~式(5),并结合文献[1],可得集中情形下双渠道供应链整体的利润函数为: ΠC=πT+πM=pT(a-kpT+ηpE+μe)+ (1-δ)pE(b-kpE+ηpT-μe)-ξe2/2。 (16) (17) 和电子渠道存在最优的零售价格 (18) 使供应链整体利润最大化。 证明求解供应链整体利润函数Π关于pT和pE的一阶偏导数,可得: kpE(δ-1)。 求解其二阶偏导数,可得Hesse矩阵: 基于命题3的结论,可得集中决策情形下供应链整体的最大化利润为: ΠC*=(δ-1)[k(a2+2aeμ+b(1-δ)(b-eμ)+ (2-δ)e2μ2)+η(2-δ)(a+eμ)(b-eμ)]/(η2 (δ2-4δ+4)+4δk2-4k2)-ξe2/2。 (19) 命题4在集中决策情形下,供应链在电子渠道和传统渠道的最优零售价格都随着传统零售商销售努力水平的提高而增大。当销售努力水平e满足0 证明对式(17)和式(18)求解关于销售努力水平e的一阶偏导数: 求解供应链最大化利润ΠC*关于销售努力水平e的一阶偏导数,由∂ΠC*/∂e>0可得: e<μ(δ-1)[2k(a-b+bδ)-η(2-δ)(a-b)]/[ξ(η2(2-δ)2+4δk2-4k2)+2μ2(k-η)(2-δ)(1-δ)],此时ΠC*是关于e的增函数;反之,ΠC*是关于e的减函数。命题4得证。 命题4表明,在集中决策情形下,传统零售商和生产商统一决策,随着销售努力水平的提高,供应链成员都可以以此来提高产品在双渠道上的零售价格,因为销售努力水平的增加意味着消费者购买效用的增加。另外,传统零售商的销售努力投入低于某边界时,供应链的整体利润随着销售努力投入的增加而增大;反之,销售努力投入的增加将会降低供应链的整体利润。因此,供应链管理者可以基于命题4选择合适的销售努力投入,从而促使供应链整体利润最大化。 由式(12)、式(13)和式(19)可得集中决策和分散决策情形下供应链整体利润差值为: 4(k2-η2)(1-δ)3[(a+eμ)(2k2-2η2+ δη2)+δηk(b-eμ)]2/[(4k(1-δ)· (k2-η2)-kδ2η2)(δ2η2-8δη2+8δk2+ 8η2-8k2)2]。 (20) 由命题3可知4(k2-η2)(1-δ)-δ2η2>0,故而可得ΔΠ>0,即在集中决策情形下供应链的整体利润大于在分散决策情形下供应链的整体利润。这是因为在分散决策情形下,传统零售商和生产商都以自身利润最大化进行决策,从而造成供应链整体利润的次优化(供应链常见的双重边际效用)。 命题5随着传统零售商销售努力投入e的增加,双重边际效用造成供应链整体利润次优化的程度越明显;电商平台的收费比率δ越大,双重边际效益亦越明显。 命题5说明,在传统的企业管理中,供应链成员的很多决策都会造成双重边际效用的加剧(例如传统零售商销售努力投入的增加);并且在双渠道供应链中电商平台的收费比率作为外部因素,也严重影响分散决策情形下供应链的整体利润。解决双重边际效用问题,学者们广泛采用收益共享契约[15-17],以确保供应链成员收益水平高于分散决策状态,达到供应链最优绩效;然而,相对于收益共享契约,采用两部定价契约,生产商可以实现供应链的纵向整合,在达到供应链整体利润最优化的同时,通过调节固定收费的范围,可使供应链成员实现帕累托绩效改进。因此,本文通过两部协调定价机制来协调供应链,促使分散决策下供应链整体利润仍能达到集中决策情形下的最大化。 在生产商主导的双渠道供应链中,为了实现供应链整体利润的最优化,生产商可以采用两部协调定价机制,生产商首先向传统零售商收取固定的费用(可以看出加盟费),然后再根据产品市场需求量确定单位产品的批发价格。两部协调定价机制在实际企业管理中被广泛的采用,例如:肯德基、海底捞等可加盟的连锁零售企业,初次加盟时,公司会收取加盟费,然后再以相应的批发价格销售产品给各加盟店;同样,电话公司通常先按月收取固定费,再按用户通话次数收取电话费;更多地,若包下一辆出租车,通常先付一笔固定费(起价),而后再按里程付费。 因此,基于销售努力的双渠道供应链中,生产商采取两部协调定价机制的具体策略为: S=G+wXqT。 (21) 式中:G≥0为传统零售商向生产商订货时需要交付的固定费用,wX为协调策略下的批发价格。在两部定价机制下,生产商可以通过调节固定费用G来分配供应链成员的利润,使供应链达到协调。 生产商制定的电子渠道的零售价格等于集中决策时的最优零售价格,即: (22) (23) wX*= (24) 因此,只有将生产商的批发价格设置为wX*,传统零售商基于自身利润最大化才会将传统渠道的零售价格设置为: (25) 从而实现供应链整体利润的最大化。命题6得证。 由命题6可得协调机制下传统零售和生产商的最优利润函数分别为: (26) (27) D1=δ2η2; A1=(1-δ)(k2-η2); B1=4(k2-η2)(1-δ)3/k; C1=((a+eμ)(2k2-2η2+δη2)+δηk(b-eμ))2。 证明考虑在两部协调定价机制下,零售商仍然进行决策,而生产商作为供应链的主导者,要实现供应链整体利润的最大化,将制定较低的批发价格(由wX* (k2-η2)-δ2η2)((a+eμ)(2k2-2η2+δη2)+ δηk(b-eμ))2/[4(1-δ)·(k2-η2)- δ2η2]2k(8(1-δ)(k2-η2)-δ2η2)2; δη2)+δηk(b-eμ))2·(k2-η2)(1-δ)3/ [k(4(1-δ)(k2-η2)-δ2η2)2(8(1-δ)· (k2-η2)-δ2η2)]。 通过数值仿真来验证上述命题,并分析供应链成员收益、利润分配、最优定价策略随相关参数的变化关系。根据第2部分模型构建时参数的假设,取偏好传统购物方式的消费者的基础需求量a=30,鉴于电子购物方式发展的时间较短,取偏好电子购物方式的消费者的基础需求量b=20,根据k>η>0,取k=0.6,η=0.4。 考虑销售努力参数对双渠道供应链定价策略、供应链成员利润变化,以及两部收费策略的影响,根据文献[1]取电商平台的收费比率δ=0.2。 图2和图3分别给出了分散决策和集中决策下供应链整体利润随销售努力水平e和销售努力对产品市场需求量敏感参数μ的变化关系。图2和图3说明,在分散决策和集中决策下,当销售努力对产品市场需求影响较小(μ较小)时,供应链整体利润随着销售努力水平的提高而增加,当销售努力水平提高到一定程度以后,供应链整体利润会随着销售努力水平的提高而下降;当销售努力对产品市场需求影响较大(μ较大)时,供应链整体利润会随着销售努力水平的提高而增加。因此,在实际的供应链决策中,存在最优的销售努力水平使供应链利润最大化,并且集中决策下最优销售努力水平大于分散决策时的最优销售努力水平。 图4显示了分散决策和两部协调定价决策下生产商和传统零售商利润随销售努力水平的变化关系。可以发现,传统零售商的利润在两种决策模式下都是先增加再降低,但协调定价下,未分配利润前,传统零售商的利润增减幅度都要小于分散决策下的利润增减幅度;然而,销售努力水平对生产商利润的影响则相反。这显示了两部定价策略下,销售努力水平对传统零售商利润的影响较小,对生产商的利润则影响加大。 图5表明两部协调定价决策下,随着销售努力水平的提高,生产商分配利润的区间越来越大,原因是销售努力水平的提高造成了生产商和传统零售商在两种决策模式下利润差距增大。从而验证了命题5。由图6可得,两种决策模式下生产商在电子渠道制定的最优零售价格随着销售努力水平的提高而降低,且分散决策下的最优零售价格低于协调决策;图7中,生产商制定的最优批发价格随着销售努力水平的提高在分散决策下增加,在协调决策下则降低。 由图6和图7可知,面对零售商销售努力水平的提高,生产商在分散决策下通过降低电子渠道零售价格和提高传统渠道批发价格来提高产品在电子渠道的市场需求量,该定价决策造成了供应链双重边际效应的加剧;而在协调决策下,生产商则通过降低批发价格,来实现供应链整体利润的最优化。图8显示了传统零售商通过提高销售努力水平来增大传统渠道零售价格,从而实现利润的在最大化,可以发现协调决策减弱了销售努力水平提高对最优零售价格增大的影响。 本节研究电商平台扣点费率对供应链定价决策的影响,取e=0.3。 表1展示了两种决策模式下供应链成员定价策略随电商平台扣点费率的变化关系。可以发现,随着电商平台扣点费率的增大,两种决策模式下电子渠道的零售价格将增加,传统渠道的零售价格先降低后增加,而批发价格则降低。这是因为电商平台扣点费率的增大,迫使生产商倾向于传统渠道销售,故而会增加电商平台的零售价格,降低批发价格,而传统零售商在扣点费率较小时降低零售价格,当扣点费率较大时则增加零售价格。同时,协调决策增强了扣点费率对供应链定价决策的影响(pX*随δ的变化率大于pD*)。 表1 分散决策和协调决策下供应链定价策略随δ的变化关系 图9和图10分别给出了在两种决策模式下供应链局部利润和整体利润随电商平台扣点费率增大的变化关系。由图9可知,供应链整体利润随电商平台扣点费率的增大先降低后增加,协调决策下的极小值点为δ=0.64,分散决策下的极小值点为δ=0.75。图10显示了随着电商平台扣点费率的增大,生产商的利润将降低,而传统零售商的利润则增加,且随着扣点费率的增大,生产商和传统零售商在两种决策模式下利润差逐渐增大。这是因为电商平台扣点费率的增加导致生产商在电子渠道的利润减少,生产商制定较高的零售价格来应对,从而降低了电子渠道的需求量,增加了传统渠道的需求量,造成传统零售商利润增加。 由图11可知,电商平台扣点费率的增加造成生产商和零售商在两种决策模式下的利润差变大,故而在两部协调定价决策下,生产商分配利润G的范围将增大。这亦说明电商平台扣点费率的增大造成供应链双重边际效应逾明显。这个结论验证了命题5。 本文以双渠道供应链为背景,构建了基于传统零售商销售努力和电商平台扣点费率的双渠道供应链定价决策模型,分析比较了分散决策和集中决策下供应链成员的最优价格策略,并利用两部协调定价策略解决分散决策时产生的供应链双重边际效应,主要研究结论和管理学启示如下: (1)建立了分散决策、集中决策、两部协调定价决策3种决策模式下的双渠道供应链定价决策模型,求解不同决策模式下的最优定价策略,实现了供应链成员利润的最大化、供应链整体利润的局部最优和全局最优化。 面对电子渠道逐步蚕食传统渠道市场份额的现象,传统零售商通过增加销售努力来提高其市场份额,本文通过构建基于销售努力和扣点费率下的双渠道供应链定价决策模型,从而获取最优的定价策略,为供应链管理者在该环境下决策提供理论、模型和实证依据,以期实现供应链局部和整体利润的最优化。 (2)研究了传统零售商销售努力对双渠道供应链定价决策以及供应链成员利润的影响。研究发现,在分散决策下,传统零售商希望通过提高销售努力水平来增加自身最大化利润,这种行为造成生产商利润的次优化,最终导致供应链整体利润的次优化。 相对分散决策,两部协调定价决策减弱了销售努力水平提高对最优定价决策的影响,亦减弱了销售努力水平提高对传统零售最优利润的影响,但增强了其对生产商最优利润的影响。在实际的供应链管理中,通过两部协调定价决策,传统零售商可以适当提高销售努力水平(命题4给出了最优销售努力水平的解析解),以实现供应链整体利润的最优化。 (3)研究了电商平台扣点费率对双渠道供应链定价决策以及供应链成员利润的影响。研究表明,面对电商平台提高扣点费率的情形,供应链管理者可以采用两部协调定价策略减弱扣点费率提高对供应链整体利润的负面影响。同时,较高的扣点费率增加了消费者在电子渠道购买产品的成本,损害了供应链整体的利润。 面对电子商务的迅速发展,特别是新冠肺炎对传统零售商的影响,在考虑电商平台扣点费率的前提下,本文研究了传统零售商提高销售努力水平对供应链定价决策的影响,提出两部协调定价策略协调供应链,得到最优的定价决策方案,使生产商和传统零售商均能获得最大化的利润,具有较强的理论和现实指导意义。但是,为了简化模型,本文只是将电商平台扣点费率作为一个外生变量来分析,并且供应链成员包括生产商和传统零售商,没有将电子商务平台作为一个决策者纳入供应链定价决策范畴内。因此,下一步的研究将考虑由生产商、传统零售商和电商平台组成的三元供应链的定价决策模型。2 模型构建与求解
2.1 分散情形下的双渠道供应链决策




2.2 集中情形下的双渠道供应链决策



2.3 两种决策模型下对比
2.4 两部协调定价机制研究





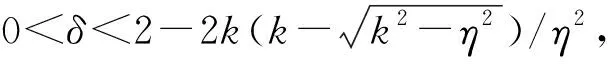
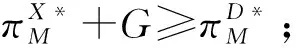
3 数值仿真
3.1 销售努力参数灵敏度分析




3.2 扣点费率参数灵敏度分析




4 结束语

