一种新的广义对数正态分布点估计方法
温录亮,陈平炎
(1.佛山科学技术学院, 广东 佛山 528225;2.暨南大学, 广州 510632)
0 引言
基于正态分布的推广和应用一直是统计学领域的热点研究问题,如2021年,魏正元等[1]提出了离散alpha偏正态分布,并分析了其性质和参数估计问题。对正态分布进行拓展,可以得到对数正态分布,目前对数正态分布已广泛应用于生命科学的不同领域,包括生物学、生存分析以及金融和风险分析等[2-3]。2005年,Nadarajah[4]提出并研究了广义正态分布的相关性质,并讨论了极大似然估计,给出了信息矩阵。在此研究基础上,2009年,Martín等[5]提出了广义对数正态分布,利用贝叶斯方法进行参数估计,并应用于分析生命周期数据。2012年,Singh等[6]对广义对数正态分布的极大似然估计和贝叶斯估计进行了对比研究。2013年,Toulias等[7]和Kleiber[8]讨论了广义对数正态分布不同条件下的矩求解问题。2017年,Li等[9]提出使用Jeffreys先验,比较了广义对数正态分布在已知先验和极大值条件下的贝叶斯估计性能。2020年,Tomazella等[10]提出了一种新的贝叶斯方法,估计了广义对数正态分布的参数并应用于生存数据分析。综上所述,相关学者针对广义对数正态分布的参数估计,主要采用极大似然估计或贝叶斯估计方法。为此,提出广义对数正态分布形状参数一种新的强相合的点估计量,并和极大似然估计、贝叶斯估计结果进行对比,评估新提出的点估计方法的性能。
在内容的编排上,第1节给出了广义对数正态分布的定义和期望方差;第2节将提出广义对数正态分布形状参数υ和σ的一种新的点估计量,给出具体的证明过程和逆变换抽样方法;第3节进行数值模拟,验证第2节定理的结论;第4节将提出的点估计和极大似然估计、贝叶斯估计结果进行对比,评估点估计性能;第5节给出结论。
1 广义对数正态分布
如果一个随机变量X服从广义对数正态分布,则其概率密度函数可以写为:
(1)
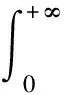
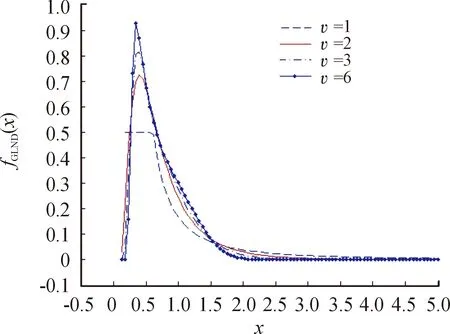
图1 广义对数正态分布的概率密度函数曲线(μ=0,σ=1)
参考文献[8,11],当υ>1时,可以推导出广义对数正态分布k阶原点矩。
命题1设随机变量X的概率密度函数为式(1),则X的k阶原点矩为:
(2)
证明根据计算公式,有:
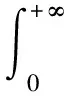
将式(1)代入,得出:
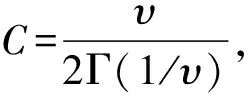
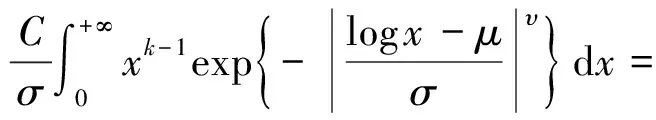
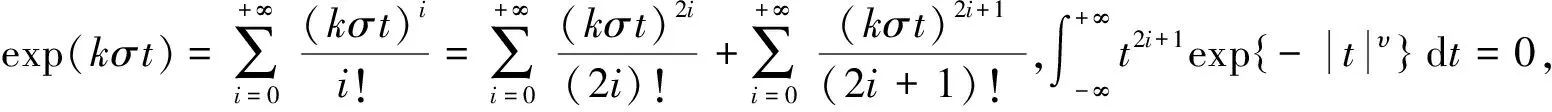
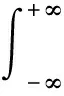
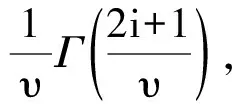
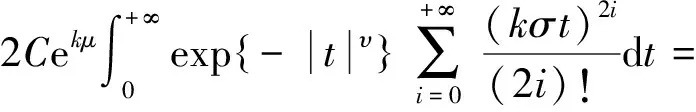
从而可以写出广义对数正态分布的期望和方差为:
利用矩估计时要注意,以上是当υ>1时的k阶原点矩。当υ<1时,k阶原点矩不存在;当υ=1时,由上述推导可知,当且仅当kσ<1时存在k阶原点矩。
2 点估计及逆变换抽样
本节通过来自广义对数正态分布总体样本的极值来估计形状参数,并证明此估计量是强相合的。具体地,设总体X服从广义对数正态分布,即其概率密度函数为式(1),X1,X2,…,Xn为来自总体X容量为n的样本,则形状参数υ的估计量为:
若υ已知,则σ的估计量为:
下面的结论表明这2个估计量都是强相合的。
定理1设随机变量X服从广义对数正态分布,X1,X2,…,Xn为来自总体X容量为n的样本,则:
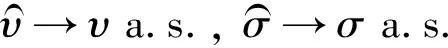
(3)
下面给出定理1的证明,先介绍一些记号和必要的引理。
设{An,n≥1}是一个事件序列,参考文献[12],记
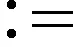
表示事件序列{An,n≥1}发生无穷多次。
运用翻转课堂是一种培养学生自主性的有效方式。“翻转教室”这一名词最早起源于美国,其具体形式为:首先学生在课外通过网络平台,观看学习老师做的教学视频,然后再由教师在课堂上进行测试,并讨论了课前记忆的知识,最后帮学生们将知识转为内化[3]。显而易见,将知识共享并实现内化是老师和学生在课堂上互相协助实现的。“翻转课堂”的特点十分明显,学生和老师的角色互换的传统教学过程是教师集中作业,学生的学习任务是事先不可知的。但在“翻转课堂”教学形式中,学生可以提前学习知识,之后在课堂上教师和学生共同学习的一种新颖方式。这样更加注重学生的自主性及在课堂上的研究,讨论与同伴以及老师的协作、交流以及反思。
下面的引理1可参考文献[13],引理2可参考文献[4]。
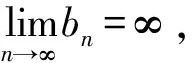
(4)
引理2如果随机变量X服从广义对数正态分布,可以得到:
(5)
命题2设{X,Xn,n≥1}是独立且恒等分布的序列,假设X服从广义对数正态分布,则可以得到:
(6)
证明不失一般性,可以假设μ=0,首先证明:
等价于证明:
对任意的ε>0,通过引理1可以得到:
P{logXn≥(1+ε)1/υσ(logn)1/υi.o.}=0
根据Borel-Cantelli引理,要证明上式,只需证明:
通过引理2,可以得到:
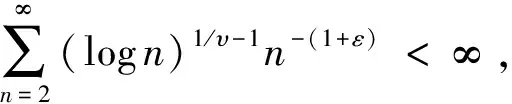
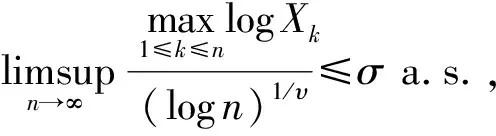
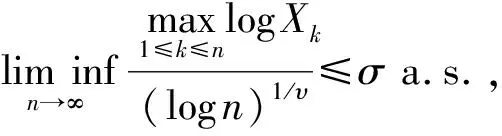
根据Borel-Cantelli引理,要证明上式,只要证明对任意的ε>0,有:
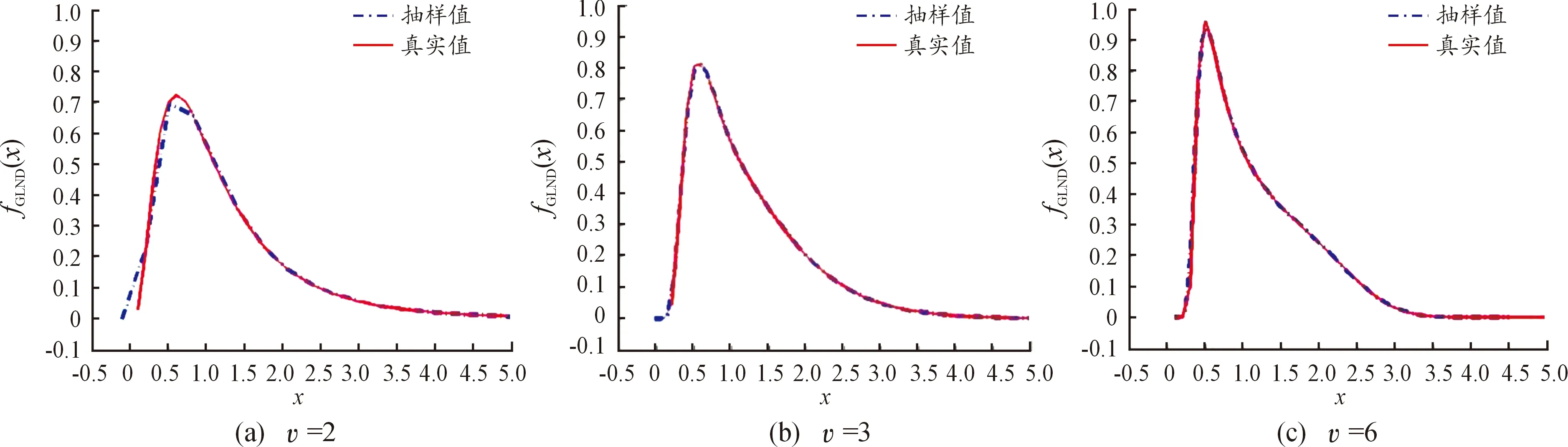
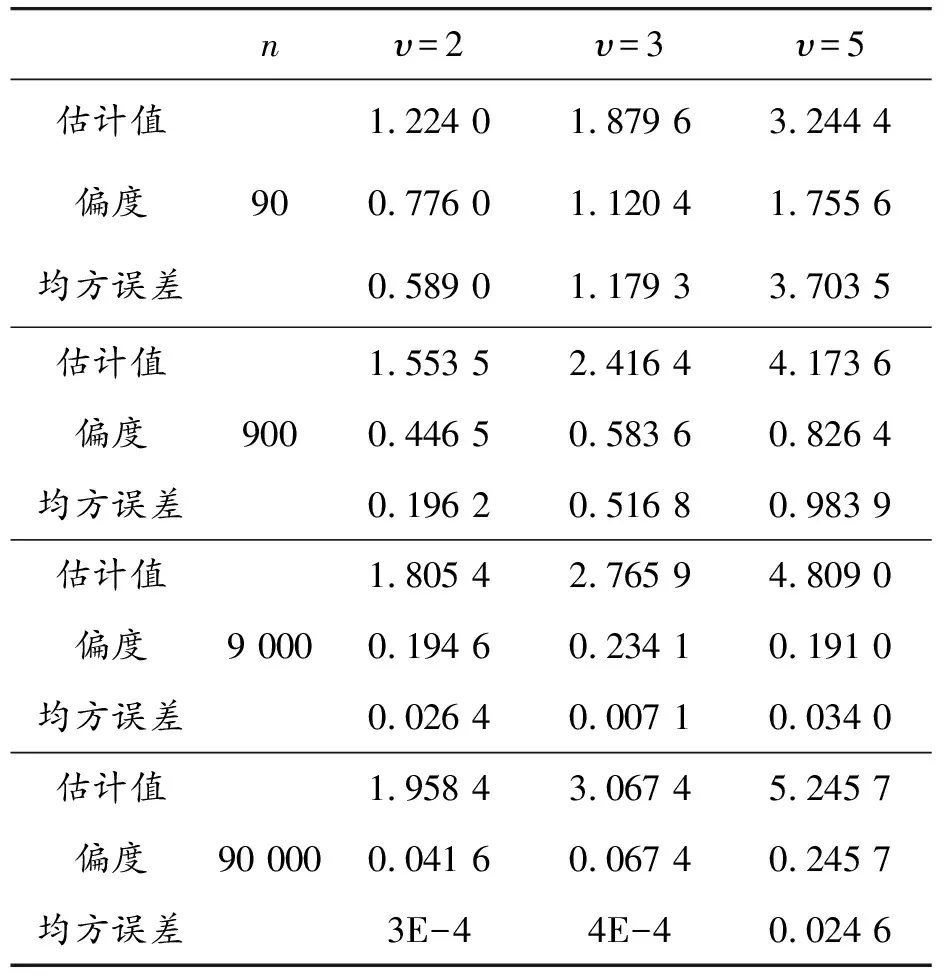
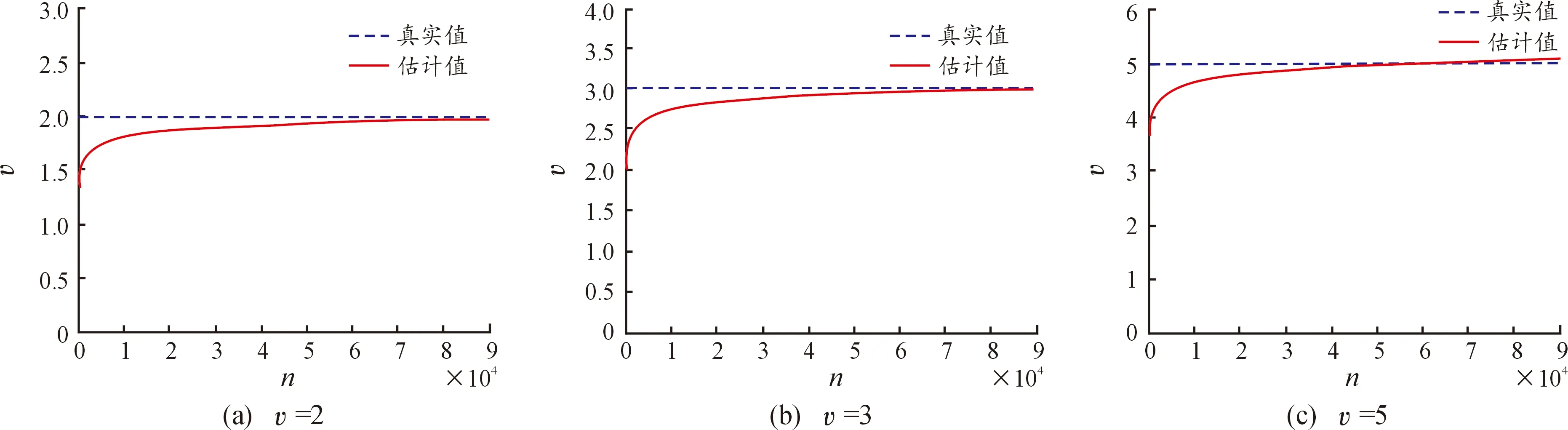
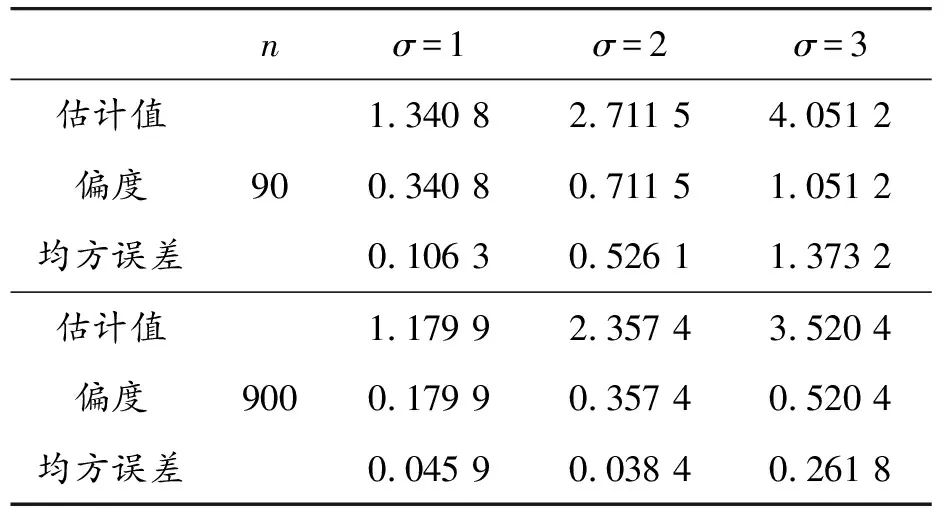
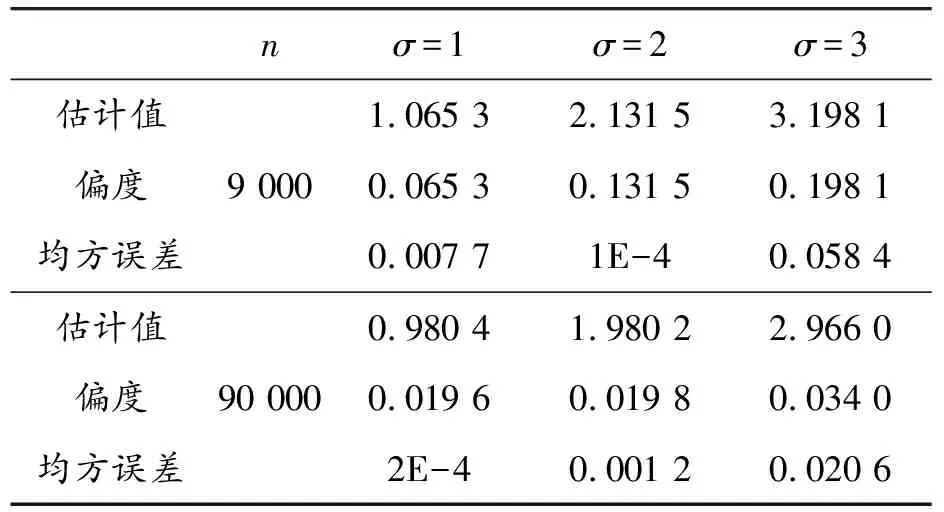
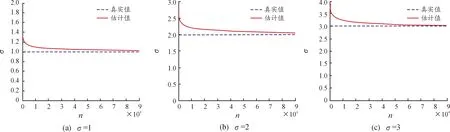
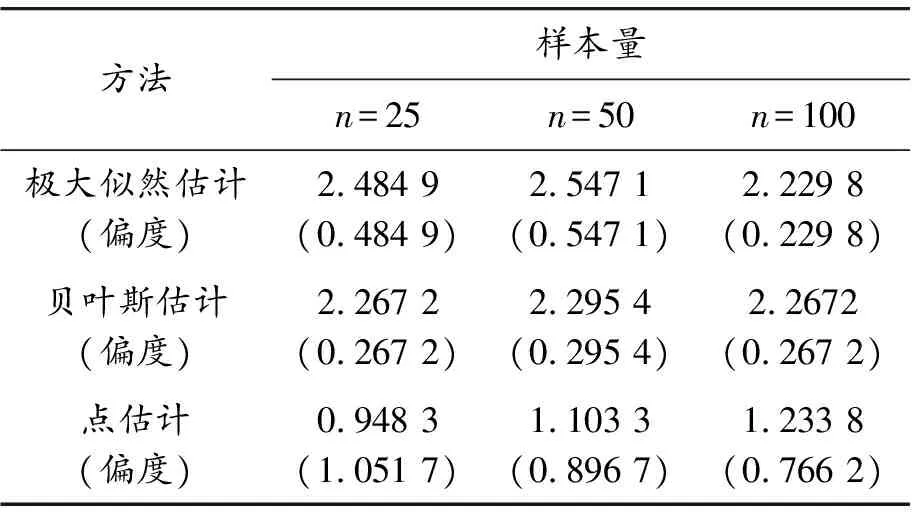
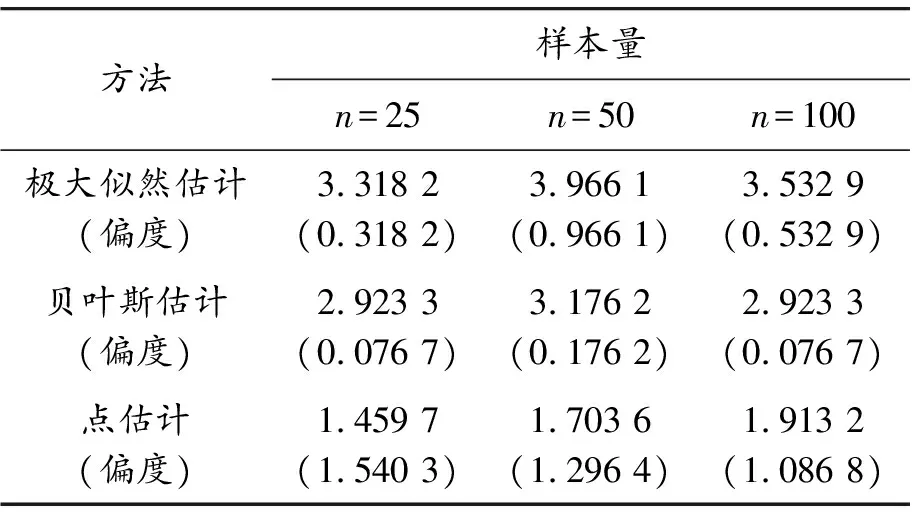
已知对任意的x>0,有1-x [1-P{logX≥(1-ε)1/υσ(logn)1/υ}]n< e-nP{log X≥(1-ε)1/υσ(log n)1/υ} 通过引理2可以得到: nP{logX≥(1-ε)1/υσ(logn)1/υ}~ 上式中的不等式对于足够大的n成立。 综上可以得到: 定理1的证明由上面推导得知当 因此: 为了对定理1进行数值模拟,需要产生相应的随机数。下面的逆变换抽样方法借鉴了文献[5,14]的思想方法。 设X、U、V是随机变量,抽样算法流程为: 步骤1设U~Γ(1+1/υ,1),产生随机数; 步骤2设V~Uniform (-1,1),产生随机数; 步骤3令X=exp(σU1/υV+μ),可以得到服从广义对数正态分布的随机数。 利用以上算法流程,选取500个随机数,可以画出抽样概率密度曲线和真实概率密度曲线的对比图。通过图2可以发现,υ取不同值时的抽样概率密度曲线和真实概率密度曲线重合度都很高,说明通过命题3提出的逆变换方法对广义对数正态分布进行抽样,效果是理想的。 图2 广义对数正态分布的抽样概率密度曲线和真实概率密度曲线(μ=0,σ=1) 本节进行数值模拟,评估广义对数正态分布的点估计性能。首先给出偏度和均方误差的公式: (7) 表1 关于广义对数正态分布参数υ的点估计结果 图3 关于广义对数正态分布参数υ的点估计量收敛效果图 nσ=1σ=2σ=3估计值偏度均方误差901.340 82.711 54.051 20.340 80.711 51.051 20.106 30.526 11.373 2估计值偏度均方误差9001.179 92.357 43.520 40.179 90.357 40.520 40.045 90.038 40.261 8 nσ=1σ=2σ=3估计值偏度均方误差9 0001.065 32.131 53.198 10.065 30.131 50.198 10.007 71E-40.058 4估计值偏度均方误差90 0000.980 41.980 22.966 00.019 60.019 80.034 02E-40.001 20.020 6 图4 关于广义对数正态分布参数σ的点估计量收敛效果图 第3节对定理1的结论进行了数值模拟验证,本节对点估计和极大似然估计、贝叶斯估计的结果进行对比。固定μ=0,σ=1,取υ=2,3,利用点估计方法仿真实验重复进行100次,求平均值得到估计结果,并和Li等[9]提出的极大似然估计、贝叶斯估计结果进行对比,如表3和表4所示。 表3 关于参数υ=2的点估计和极大似然估计、贝叶斯估计的结果 表4 关于参数υ=3的点估计和极大似然估计、贝叶斯估计的结果 通过表3和表4可以发现,针对参数υ,在样本量分别为n=25,50,100的情况下,利用提出的点估计方法,得出参数估计结果的偏度值明显大于极大似然估计和贝叶斯估计得出的结果。所以说,如果样本量较小,利用极大似然估计或贝叶斯估计是合适的,而利用点估计则会产生较大误差。如果样本量较大(如超过10 000),建议考虑选用点估计方法。相对于其他估计方法,提出的这种新点估计方法更加简单易算。 提出了广义对数正态分布形状参数υ和σ的一种新的点估计量,给出了推导证明过程,利用逆变换抽样方法进行数值模拟,可以看到随着样本量n的增大,估计值越来越收敛于真实值,和定理1的结论一致。和广义对数正态分布的极大似然估计、贝叶斯估计结果进行对比,发现这种新的点估计方法不适用小样本估计,而适用于大样本估计,在进行相关大数据分布模型参数估计时,具有推广应用价值。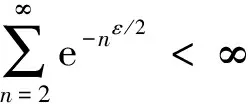
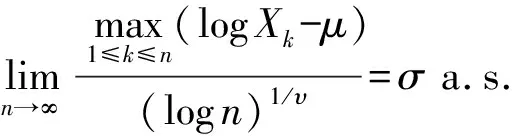
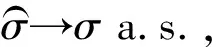
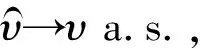
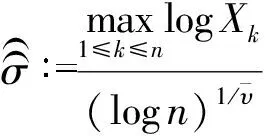
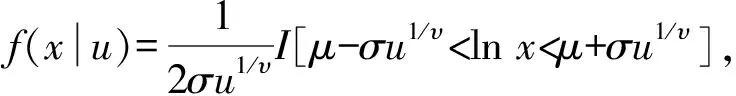
3 数值模拟
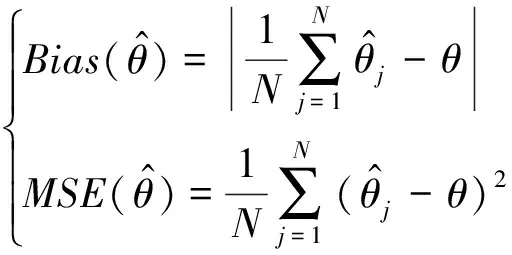
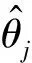
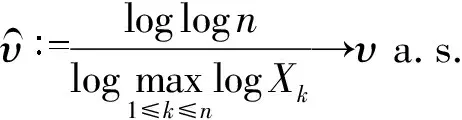
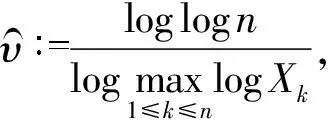
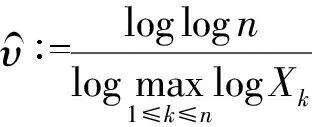
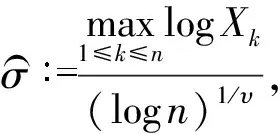
4 参数估计效果对比
5 结论

