具有无限马尔可夫二维Roesser系统的模糊H∞状态反馈控制

叶志勇，严 芳，罗小玉，何 鑫，赵红霞

(1.重庆理工大学 理学院， 重庆 400054；2.重庆人文科技学院 机电与信息工程学院， 重庆 401524)

0 引言

众所周知，马尔可夫跳跃系统在模拟突变结构和参数变化方面具有一定的研究意义。值得注意的是，现有的大多成果都是在有限状态空间马尔可夫链条件下进行的。近年来，具有无限状态空间马尔可夫跳系统引起了学者们的密切关注[5]，人们已经认识到，有限马尔可夫跳系统和无限马尔可夫跳系统的性能存在本质的区别。文献[6]讨论了对于平稳的有限马尔可夫跳系统，随机稳定性等价于渐近均方稳定性，但在无限状态空间马尔可夫链情况下则并非如此。文献[7]研究了带无限状态马尔可夫链的离散时间不确定时滞系统的稳定性，讨论了系统渐近均方稳定性、随机稳定性、均方指数稳定性等之间的关系。

一般来说，T-S模糊模型的优点是通过对局部线性系统模型的“混合”，来逼近任意光滑非线性函数，从而使线性控制系统理论有助于解决非线性问题。文献[8]研究了基于Fornasini-Marchesini (FM)局部状态空间模型建立二维离散模糊系统模型的稳定性分析问题。文献[9]研究了离散时间非线性二维Roesser模型系统的镇定问题。文献[10]考虑了第二FM模型下基于观测器的二维T-S模糊系统的H∞控制器设计。文献[11-12]解决了Roesser模型的控制问题。文献[13]研究了用Roesser模型描述的T-S模糊系统的耗散性分析和控制器设计问题。文献[14]针对二维离散切换系统的H∞鲁棒控制器设计问题，采用具有多面体不确定性的Roesser模型来描述。文献[15]利用T-S模糊模型方法解决了一类受规定干扰衰减水平影响的非线性网络控制系统的事件触发滤波问题。

目前，带有无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定的H∞控制问题仍然是一个非常有趣且具有一定挑战性的问题。也很少有工作去处理这个问题，这主要是因为二维Roesser系统、无限状态空间马尔可夫链和T-S模糊模型的性质所引起的数学复杂性。因此，带有无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定的H∞控制问题的成果并不多，这推动了笔者的研究。

主要研究了对带有无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定的H∞控制问题。首先介绍了Roesser模糊模型系统的预备知识，通过构造Lyapunov函数以及线性矩阵不等式方法证明了带无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定性和H∞控制问题，并用一个特例验证其有效性和实用性。

1 基础知识和模型建立

1.1 符号说明

1.2 模型描述

在(M,F,P)空间上考虑一个二维离散时间T-S模糊Roesser模型系统如下：

规则kIfθ1(i,j) isMk,1，andθ2(i,j) isMk,2,…,θg(i,j) isMk,g，then

(1)

这里θ(i,j)=[θ1(i,j),θ2(i,j),…,θg(i,j)]是前提变量；Mk,l对l=1,…,g是模糊集，xh(i,j)∈Rnh是水平方向状态，xv(i,j)∈Rnv是垂直方向状态，u(i,j)∈Rnu是控制输入，ω(i,j)∈Rnω是外部干扰，y(i,j)∈Rny是可测输出，r是模糊规则数。其中

是已知相应维数的实值矩阵，并且他们都是马尔可夫链γi, j的函数。

γi, j在无限可数集K1={1,2，…}中取值，转移概率矩阵Θ1=(Λpq)，Λpq形式如下：

Pr{γi+1, j=q|γi, j=p}=Pr{γi, j+1=q|γi, j=p}=Λpq

(2)

根据概率论，Λpq满足如下条件：

(3)

对∀p,q∈K1。系统(1)的边界条件(X0,Γ0)定义如下：

(4)

同时，将零边界条件定义为：

xh(0,j)=0,xv(i,0)=0,i,j=0,1,2,…

进一步在X0上作出如下假设。

假设1假设X0满足下列条件：

(5)

这里E{·}表示数学期望，|·|表示欧式范数。

模糊集函数定义如下：

(6)

这里μk,l(θl(i,j))是在模糊规则数k上θ(i,j)的隶属度。通过定义有：

基于模糊规则，T-S模糊Roesser模型可以推断如下：

(7)

其中：

本节采用了状态反馈控制中常用的假设，假设γi, j的精确值难以获得，设计状态反馈控制器如下：

(8)

这里K(ηi, j)表示控制增益，它依赖于参数ηi, j∈K2(K2={1,2,…})，ηi, j是变量控制的模式，同时它的条件概率Λps可以由γi, j得到，即：

Pr{ηi, j=s|γi, j=p}=Λps

(9)

Θ2=(Λps)为条件概率矩阵，同样满足：

将γi, j、γi+1, j(γi, j+1)、ηi, j简记为p、q、s，如A(ηi, j)简记为Aq。

把式(8)代入式(7)得到闭环动态系统如下:

(10)

其中：

Gps=Ap+BpKs,Hps=Cp+DpKs

注:本节得到的闭环系统形式上与文献[12]的闭环系统相似，是在此基础上向T-S模糊模型、无限状态空间的马尔可夫链进行的推广。

为了进一步研究对带有无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定的H∞控制问题，给出如下定义。

定义1当闭环二维系统(10)中外部扰动输入ω(i,j)=0时，如果对任何边界条件(X0,Γ0)满足如下条件：

(11)

则闭环系统(10)被称为渐近均方稳定。

(12)

则闭环系统(10)有H∞性能指标μ。

2 主要结论

(13)

(14)

证明构造李亚普诺夫函数如下：

V(i,j)=xT(i,j)Rpx(i,j)

定义：

ΔV(i,j)=x1T(i,j)Rqx1(i,j)-xT(i,j)Rpx(i,j)

(15)

根据状态方程(10)，当ω(i,j)≡0时，很容易得到：

(16)

(17)

通过舒尔补引理，从式(14)得到：

(18)

结合式(17)和式(18)，可得：

(19)

(20)

这里m1,m2是正整数。

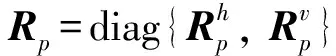
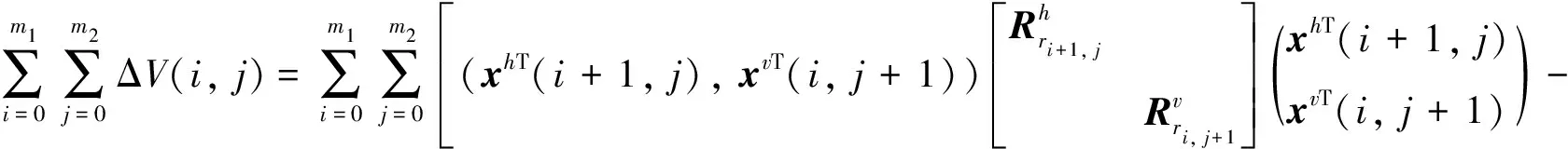
(21)

通过式(20)和式(21)可以推得：

(22)

(23)

由假设1中的式(5)，有

(24)

则式(11)满足，故闭环系统(10)渐近均方稳定。得证。

进一步地，讨论基于零边界条件下的H∞性能指标。

记

则式(14)等价于如下矩阵：

(25)

通过舒尔补定理，等价矩阵(25)可以等价于如下不等式：

(26)

通过闭环系统(10)，得到：

(27)

(28)

(29)

结合式(27)和式(28)，可得：

E{yT(i,j)y(i,j)-μ2ωT(i,j)ω(i,j)+ΔV(i,j)}=

(30)

只要条件(13)(26)成立，即得到J<0，可以推得：

(31)

在零边界条件下，又由式(21)(29)(30)，得到：

(32)

综上所述，对无限状态空间马尔可夫链的模糊Roesser模型，根据定义2，则式(12)满足，故定理1得证。即最终得到了关于无限状态空间马尔可夫跳的模糊Roesser模型系统在假设1条件下的渐近均方稳定和H∞控制的充分条件。

接下来，给出一个实例的仿真模拟来验证其定理的有效性以及实用性。

3 仿真模拟

在本节中，基于文献[16-17]将提供一个实例来说明所提出方法的有效性。在现实世界中，有些气体吸收、水流加热的动力学过程和空气干燥可以如下公式表示：

b(γi, j)u(x,t)+e(γi, j)ω(x,t)

(33)

其中：f(x,t)是关于空间x∈[0,xf]和时间t∈[0,∞]的未知函数；a0(γi, j),a1(γi, j),a2(γi, j),a3(γi, j),b(γi, j),e(γi, j)是关于γi, j的函数；ω(x,t)是输入扰动，u(x,t)是控制输入。定义：

(34)

则微分方程(33)可转化为以下二维状态空间模型：

(35)

为了得到非线性系统的二维T-S模糊模型，考虑以下2个规则：

规则1If sin2(xv(x,t)) is about 0，then

(36)

规则2If sin2(xv(x,t)) is about 1，then

(37)

二维T-S模糊系统的隶属函数是：

h1=cos2(xv(x,t)),h2=sin2(xv(x,t))

接下来，将上述T-S模糊系统离散化为采样时间T1和T2，对应于变量x和t。因此，带无限马可夫离散二维模糊系统由下式给出：

规则1If sin2(xv(x,t)) is about 0，then

(38)

规则2If sin2(xv(x,t)) is about 1，then

(39)

取T1=T2=0.1,a0(γi, j)=4,a1(γi, j)=-8,a2(γi, j)=-8以及b(γi, j)=-4,e(γi, j)=-4，得到系统相对应的参数矩阵如下：

为了研究系统(1)的H∞控制问题，令式(1)中相应的参数矩阵为：

其中转移概率矩阵Θ1=(Λpq),Θ2=(Λps)为：

得到式(8)中反馈控制的反馈增益矩阵为：

利用Matlab对系统进行模拟，模拟结果如图1—3所示。模拟结果表明H∞控制中参数的最小值为u2=4。

图1 有控制输入的水平状态

由图1和图2可以看出，二维系统水平方向与垂直方向一开始波动比较大，但在一段时间后都渐近的逼近于零。因此证明了定理1。

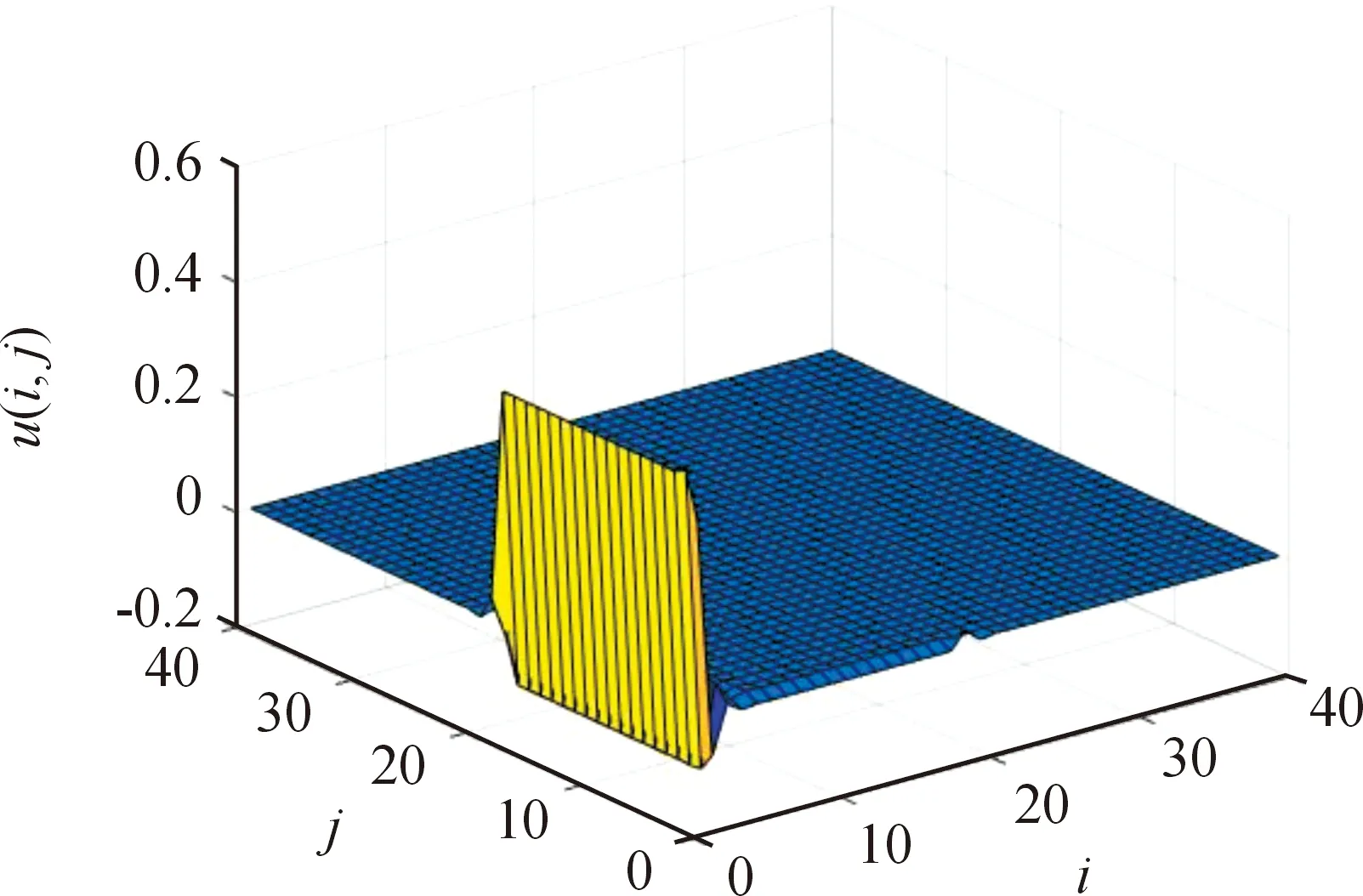
图3 控制输入图

4 结论

目前的研究中，通常都是对二维Roesser模型H∞控制的研究；但带有无限状态空间马尔可夫链的二维Roesser T-S模糊模型系统的渐近均方稳定的H∞控制问题仍然是一个非常有趣和具有挑战性的问题。基于T-S模糊模型，研究了一类离散时间无限状态空间马尔可夫跳二维Roesser模型系统的渐近均方稳定性与H∞控制，并且通过构建李雅普诺夫函数，利用线性矩阵不等式给出了证明。利用Matlab模拟出的结果表明H∞控制中参数的最小值为u2=4，验证了理论的有效性和实用性。