蜗杆蜗轮减速机的非线性规划设计

高清冉，刘波，赵国正

(济源职业技术学院 机电工程学院，河南 济源 459000)

一、蜗杆蜗轮减速机优化设计基础

蜗杆蜗轮减速机是一种动力传递机构，利用蜗杆蜗轮啮合的大传动比，将电机(马达)的高转速一次性快速减小到低转速，大幅提高转矩。在传递动力与运动的机构中，由于蜗杆蜗轮传动工作平稳、噪声小、结构紧凑，还可以实现自锁等优点，蜗杆蜗轮减速机的应用范围相当广泛[1]。但一般的蜗杆蜗轮由于相对滑动速度较大，蜗轮磨损严重，故蜗轮齿圈常需用贵重的锡青铜等耐磨金属材料制造。为了降低制造材料成本，在蜗杆蜗轮减速机的优化设计中，常以降低蜗轮齿圈体积作为设计目标。

某矿运送矿渣的带式运输机用单级普通圆柱蜗杆减速机，其输入功率P=10 kW，转速n=1450 r/min，传动比i=20，单向传动，载荷无冲击(载荷系数K=1.1)。蜗杆选用低碳合金钢20 CrMnTi，芯部调质处理，齿面渗碳淬火，硬度大于45 HRC；蜗轮选用锡青铜 ZCuSn10Pb1，金属模铸造。蜗轮齿圈的许用接触应力σH=220 MPa。按照设计要求对蜗轮齿圈体积进行优化设计，并设计蜗杆蜗轮尺寸。

二、建立数学模型

(一)确定齿圈体积计算公式

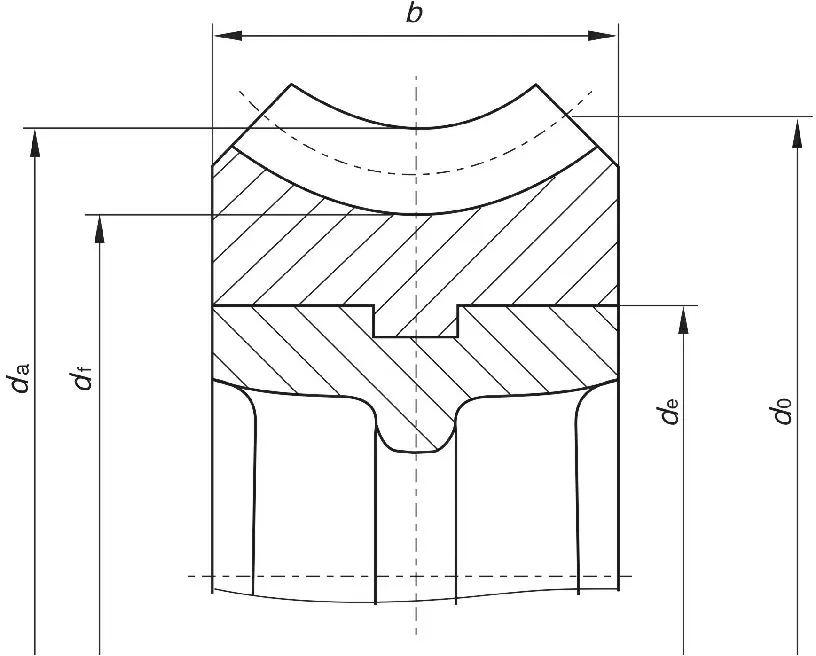
注：b—齿宽；de—齿圈外径；d0—齿圈内径；da—齿顶圆直径；df—齿根圆直径。

根据机械设计手册[2]，确定计算项目及其计算公式如表1所示。

表1 计算项目及其计算公式

根据表中几何尺寸，计算齿圈体积V：

(二)确定设计变量

由齿圈体积的计算公式可知，齿圈体积是关于蜗杆头数z1、模数m、直径系数q和传动比i的函数，通常传动比i是设计已知量，因此取z1、m、q作为设计变量[3]：

(三)确定目标函数

齿圈体积作为目标函数，写成式(1)：

(1)

(四)确定约束条件

1.确定接触约束条件

由机械设计手册，确定蜗轮齿面接触疲劳强度条件：

其中T2是蜗轮的扭矩，单位N·mm，σH为蜗轮的许用接触应力，单位MPa。把z2=i×z1，x1=z1，x3=q带入上式，整理后得到接触约束条件式(2)：

(2)

蜗轮的齿根弯曲疲劳强度：由于蜗轮的抗弯能力强，不容易发生轮齿折断，通常不进行蜗轮齿根弯曲强度计算[4]。

2.确定蜗杆刚度约束条件

蜗杆工作时，其最大挠度y小于等于0.001d1=0.001mq，即

蜗杆支承跨度L≈0.9d2=0.9miz1；

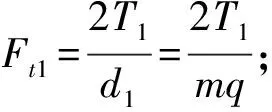
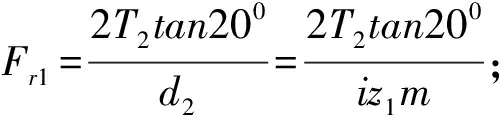
弹性模量E=2.1×105MPa

157.5πx22x3(x3-2.4)4≤0。

(3)

3.确定蜗杆头数约束条件

对于蜗杆动力传动，通常取z1=2～4，所以有

g3(X)=x1-4≤0，

(4)

g4(X)=2-x1≤0。

(5)

4.确定模数约束条件

对于蜗杆动力传动，为了保证轮齿的抗弯能力[5]，中轻载要求3≤m≤5，所以有

g5(X)=x2-5≤0，

(6)

g6(X)=3-x2≤0。

(7)

5.确定蜗杆直径系数约束条件

通常取5≤q≤18，因此有

g7(X)=x3-18≤0，

(8)

g8(X)=5-x3≤0。

(9)

由上面分析可知式(1)—式(9)组成蜗杆蜗轮的优化设计数学模型[6]。该数学模型是由2个性能约束和6个边界约束组成的三维非线性规划问题，共有8个不等式约束。

(五)建立优化设计数学模型

f(X)=0的解一般通过代数几何来求解，s.t.是英文“subject to”的缩写，意为“受约束于”[7]。优化设计问题的数学模型包括N维设计变量X、约束条件(g(X)≤0或h(X)=0)和目标函数f(X)三要素，其数学模型实质是优化问题的数学抽象，在满足所有约束条件的情况下，求解N维设计变量X，使设计目标函数达到最优[8]。最优化问题一般称为“数学规划问题”，求解约束非线性规划问题的MATLAB 函数是它要求目标函数、约束函数和函数梯度都是连续的，该函数根据初始值来进行梯度步长收敛，能够搜索到局部最优解[9]。这时蜗杆蜗轮非线性规划问题优化设计的数学模型表示为：

三、编写程序

程序根据传动比i=20，选取蜗杆头数z1=2，查表选取模数m=5，q=18，则初始点X0=[2，5，18]T，根据设计变量的边界条件、约束条件的变量系数矩阵和常数向量，编制目标函数wg_f和约束函数wg_g。

计算蜗杆传动的动力参数前，先计算蜗杆传动效率[10]：

(一)编写动力参数程序

蜗杆蜗轮动力参数程序如下：

K=1.1；P1=6；n1=1450；i=20；sigma_HP=220；

eta=1-0.035*sqrt(i)；T1=9550*P1/n1；T2=i*eta*T1

用MATLAB运行结果如图2所示。

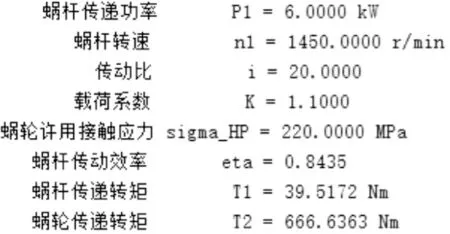
图2 蜗杆蜗轮动力参数

(二)蜗杆蜗轮约束优化

1.建立目标函数文件wg_f.m

function f=wg_f(x)；

i=20；psi_e=1.5；psi_b=0.75；

a1=pi*psi_b*x(2)^3*(x(3)+2)/4；

a2=(i*x(1)+psi_e+2)^2；

a3=(i*x(1)-4.4)^2；

f=a1*(a2-a3)；

end

2.建立约束函数文件wg_g.m

function[g，geq]=wgcd_g(x)；

K=1.1；P1=6；n1=1450；i=20；sigma_HP=220；

eta=1-0.035*sqrt(i)；T1=9550*P1/n1；T2=i*eta*T1；

g(1)=K*T2*(15150/(i*x1*sigma_HP))^2-x(2)^3*x(3)；

g2_1=0.729*i^3*x(1)^3*sqrt((2*T1/(x2*x3))^2+，

(2*T2*tan(pi/9)/(i*x1*x2))^2)；

g2_2=157.5*pi*x2^2*x3*(x3-2.4)^4；

g(2)=g2_1-g2_2；

g(3)=x1-4；

g(4)=2-x1；

g(5)=x2-5；

g(6)=3-x2；

g(7)=x3-18；

g(8)=5-x(2)；

geq=[]；

end

3.函数优化

非线性规划设计程序编写：

x0=[2；5；18]；

lb=[2；3；5]；

ub=[3；5；18]；

A=[]；b=[]；

Aeq=[]；beq=[]；

[x，fval]=fmincon(@wg_f，x0，A，b，Aeq，beq，lb，ub，@wg_g)；

蜗杆蜗轮传动优化结果如图3所示。

图3 目标函数优化结果

约束函数最优解的函数值如图4所示。

图4 约束函数优化结果

(三)计算蜗杆蜗轮主要尺寸

根据机械设计手册，编写如下程序：

z1=input(‘ z1=’)；

m=input(‘ m =’)；

q=input(‘q =’)；

Vz=wg_f([z1m q])；

fprintf(‘ Vz = %3.4f mm^3 〗n’，Vz)

d1=q*m；z2=i*z1；d2=z2*m；

a=0.5*(d1+d2)；

da1=d1+2*m；da2=d2+2*m；

df1=d1-2.4*m；

b1n=2*round((8+0.06*z2)*m/2)；

gama=atan(z1/q)；

Sn=0.5*pi*m*cos(gama)；

psi_e=1.5；psi_b=0.75；

b2m=round(psi_b*da1)；

de2m=da2+psi_e*m；

运行程序，输入z1=3，m=5，q=8后得到优化后的齿圈体积 Vz= 692787.4481mm3。

蜗杆蜗轮的几何尺寸如图5所示。

图5 蜗杆蜗轮几何尺寸

四、结语

X0=[z1，m，q]T=[2，5，18]T，初始蜗轮齿圈体积V0=wg_f(x0)；运行程序，得到蜗轮初始齿圈体积V0= 920226.4844mm3。而最优结果X=[z1，m，q]T=[3.000，5.000，7.7277]T，fmin(X)= 673921.3360mm3，极小点满足约束条件。取值z1=3，m=5，q=8后得到优化后的齿圈体积 Vz= 692787.4481mm3。根据机械设计手册，优化结果结合国家标准，规范取值为z1=3，m=5，q=10，作为优化后实际标准取值，此时得到实际优化齿圈体积Vz= 831344.9377mm3，和初始值蜗轮齿圈体积V0相比，优化设计凑整后的解是原设计结果的 0.9034倍，齿圈体积明显缩小。其缩小的主要原因是增加了蜗杆头数Z1，降低了蜗杆直径系数q，降低了蜗杆齿顶圆直径da1，而蜗轮齿宽b随着da1的降低而降低，从而得到减小齿圈体积Vz的目的。由上述设计结果可知，用MATLAB设计蜗杆蜗轮减速器，主要几何尺寸设计能够通过编写m文件运行程序完成；设计中用非线性规划优化齿圈体积降低重量，在满足使用要求的前提下，不仅降低了制造成本，同时使减速器结构也更加紧凑。