基于深度强化学习的驾驶仪参数快速整定方法

万齐天，卢宝刚，赵雅心，温求遒，*

（1.北京理工大学宇航学院，北京 100081；2.北京航天长征飞行器研究所，北京 100076；3.中国运载火箭技术研究院，北京 100076）

0 引 言

自动驾驶仪的主要任务为控制和稳定飞行器飞行，消除干扰引起的飞行器姿态变化，使飞行器按照期望的飞行轨迹或飞行姿态飞行［1］。作为一种经典的过载驾驶仪设计结构，三回路驾驶仪以其良好的性能在飞行器控制领域得到了广泛的应用。三回路驾驶仪的设计过程中需对二阶根自振频率的进行设计，文献［2-5］采用求解关于稳定裕度的非线性方程来得到合适的二阶根自振频率。然而，传统驾驶仪设计方法采用非全局剖面状态进行控制参数设计，导致其对全局约束和性能指标的考量不足。当飞行环境存在较大的不确定性时，会导致飞行器对标称轨迹跟踪制导方式的自主性和鲁棒性较差。

近年来，深度强化学习方法的发展［6-9］为飞行器智能控制实现提供了新的可能。强化学习［10-13］是一种基于动态规划求解框架的无模型马尔可夫决策过程（Markov decision process，MDP）处理方法，通过智能体与环境的不断交互和迭代学习，找到可以让智能体获取最大收益的最优策略。深度强化学习的弱模型特性和可迁移性相比于传统控制优化方法具有更广泛的适用性，在飞行器控制系统设计中有着良好的应用前景。目前，深度强化学习方法在智能控制领域已取得一定研究成果［14-23］。文献［24］利用反向传播神经网络算法作为值函数的逼近策略，对舵机动作池进行了离散处理并训练得到控制策略。文献［25］利用强化学习及自适应动态规划原理，设计了一种适用于微小型弹药的两回路驾驶仪，并建立了纵向通道控制模型。文献［26］提出了一种基于深度强化学习的智能比例-积分-微分（proportional-integral-differential，PID）控制器，实现了对过载指令的精确跟踪。但目前采用深度强化学习的控制设计方法存在训练参数维数过大、策略学习效率不高、算法不易收敛等问题，如何提升深度强化学习方法在飞行器驾驶仪领域的实用性成为了亟待解决的问题。

本文提出一种基于深度强化学习的三回路驾驶仪参数自整定方法，采用近端策略优化算法，针对驾驶仪控制参数设计造成的训练速度慢、奖励函数收敛性不好等问题进行优化改进。通过解析法得到从三维控制变量转换为一维设计参量的关系式，对深度强化学习训练数据的维度进行了简化，提高了算法的效率和奖励函数收敛性。本文内容安排如下：第1部分提出了以驾驶仪极点配置为核心的控制参数快速设计方法；第2部分构建了离线深度强化学习训练叠加在线多层感知器神经网络实时计算的智能控制架构；第3部分以典型再入飞行器为例，完成深度强化学习训练和神经网络部署，并进行了仿真验证。

1 控制参数快速设计方法

如图1所示，当前很多飞行器上采用了三回路驾驶仪结构，可采用极点配置法对其设计控制参数。各动力学参量定义可参考文献［27］。

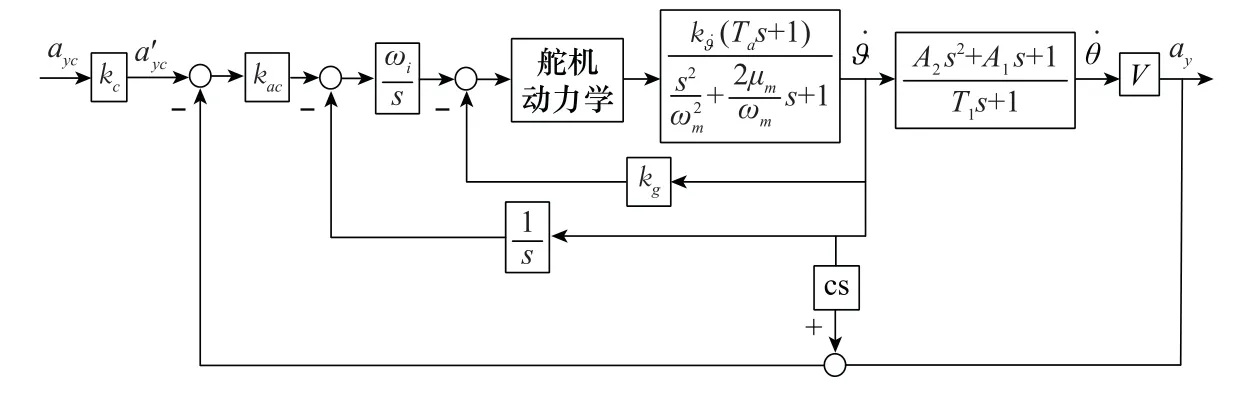
图1 驾驶仪结构图Fig.1 Diagram of autopilot structure

三回路驾驶仪主导极点为一负实根，由时间常数τ决定，直接决定了系统响应的主要特性。非主导极点由一对振荡根组成，并可由自振频率ω与阻尼μ表示。这两个参数中，阻尼决定了二阶系统振荡特性，为保证系统好的动态特性，通常设计中期望其值在0.7左右。而二阶根自振频率ω则往往很难提出绝对合理的设计约束。

略去舵机、角速度陀螺、结构滤波器及过载计的动态特性，将系统在舵机所处位置断开，得到系统开环传递函数为

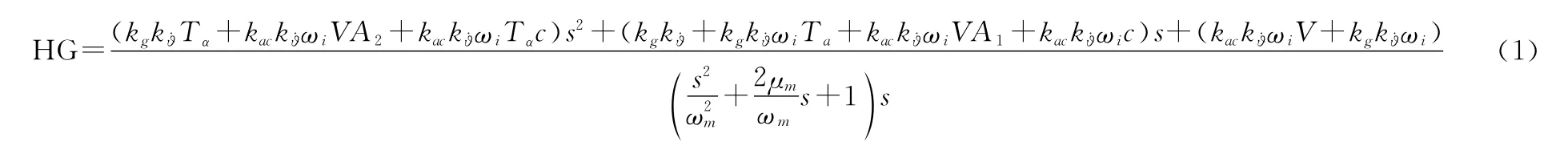
待设计的控制变量有k g、ωi、k ac，可根据三回路驾驶仪设计经验对设计参数进行简化。根据文献［2］推导可得驾驶仪设计参数k g，ωi，k ac的设计表达式为

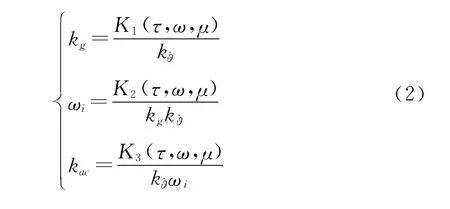
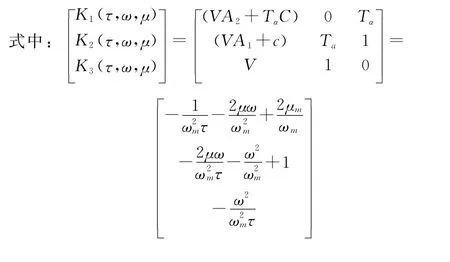
各动力学参量定义可参考文献［27］，计算所需各变量值为

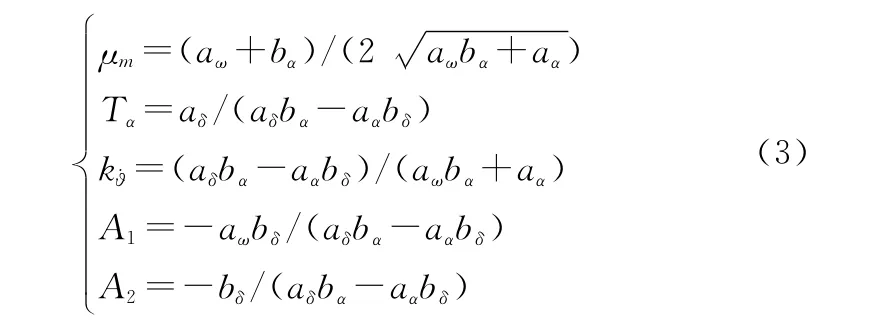
由此可将驾驶仪控制变量k g、ωi、k ac的设计转化为设计参量τ、ω、μ的设计。通常μ给定为0.7，τ由驾驶仪快速性确定，而ω在设计中很难确定。通过已有文献证明［2］，ω的变化对相位裕度P m和幅值裕度G m具有明显影响。可通过求解ω关于稳定裕度P m的非线性方程，使稳定裕度不断接近理想设计指标，最终完成自振频率ω的迭代求解。由此可得到将三维控制参数设计转化为一维设计参量ω设计的快速设计方法。

2 基于深度强化学习的驾驶仪参数自整定方法

以第1节推导的控制参数快速设计方法为基础，构建面向飞行器全飞行包络范围的近端策略优化（proximal policy optimization，PPO）离线训练方法，使得可以快速完成对设计参量在线调节的多层感知器（multi-layer perception，MLP）神经网络的训练。将训练完成的MLP神经网络进行在线部署，根据当前实际的飞行状态，由MLP神经网络实时计算得到设计参量，并直接调用快速设计方法中的极点配置解析计算方程，从而快速完成控制参数的自适应调整。采用深度强化学习控制参数自整定的飞行器制导控制方案如图2所示。

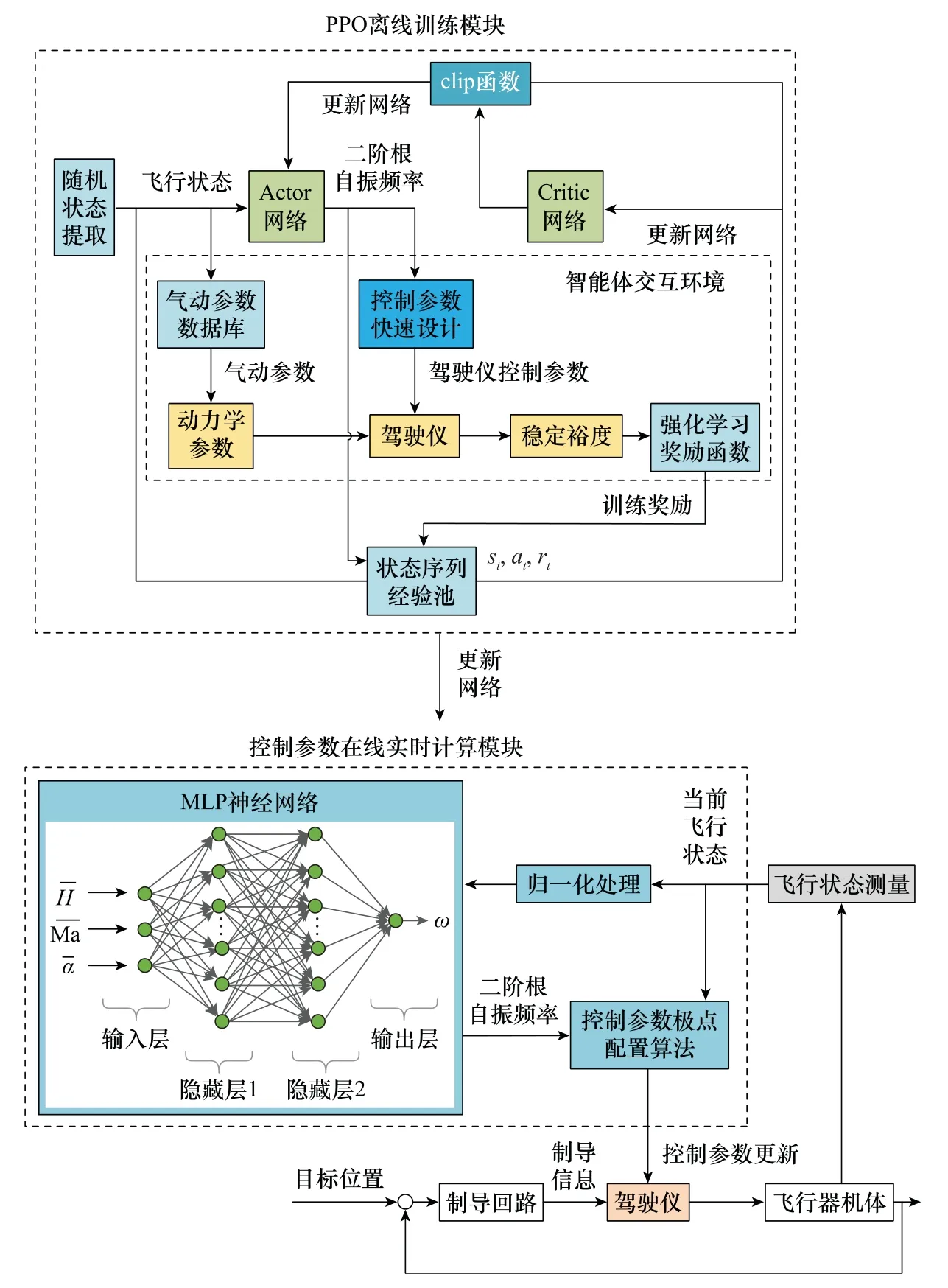
图2 基于深度强化学习方法的参数整定框架Fig.2 Parameter tuning framework based on deep reinforcement learning

2.1 PPO算法

PPO算法［28］为策略梯度类算法，其思路与信赖域区间策略优化（trust region policy optimization，TRPO）算法［29］一致，都是想在优化时采取尽可能大的步幅但又不能太大以至于产生崩坏。相比于TRPO算法，PPO算法实现起来更简单，泛化能力更强。该方法交替进行与环境的相互作用与数据采样过程，并利用随机梯度上升方法优化目标函数。相比于标准的策略梯度方法需对每个数据样本执行梯度更新，PPO算法提出一种允许小批量数据进行多周期更新的目标函数。PPO算法相比于其他算法鲁棒性更好，这与其使用的最大期望算法有关，保证了PPO算法每次更新策略总能让性能获得单调的提升。PPO算法对其超参数的变化不敏感，相比于其他深度强化学习算法，PPO算法的调参过程更加简便。

策略梯度方法采用带有一个参数（通常用θ表示）的函数来建模，直接对策略本身进行优化。策略优化的目标函数定义为

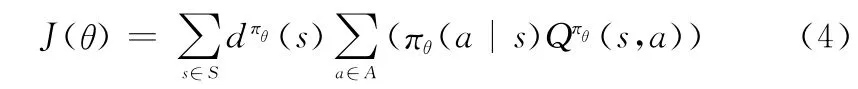
式中：s为当前状态值；a为当前动作值；S为策略分布函数的状态空间；A为策略分布函数的动作空间；（s）为由πθ决定的马尔可夫平稳分布；πθ（a｜s）为带参数θ的行为策略；Qπθ（s，a）为服从策略πθ的行为价值函数。

通过计算目标函数的梯度ΔθJ（θ），将参数θ向某个特定的方向移动，以使策略πθ可以最大化最终收益。目标函数梯度表示为

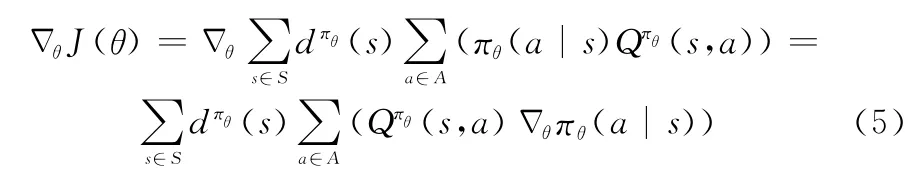
为了减小策略梯度的方差，可引入基线对行为价值函数（s，a）进行处理［30］，得到优势函数：

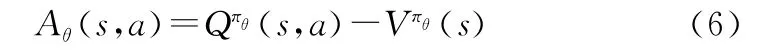
式中：（s）为引入的基线。

由于状态价值函数（s）由价值函数网络学习得到，与实际值之间存在偏差，尤其在训练初期偏差较大。可采用泛化优势估计（generalized advantage estimator，GAE）法［31］对优势函数进行估计，并通过调节参数来平衡方差与偏差。采用GAE方法的优势函数估计值为

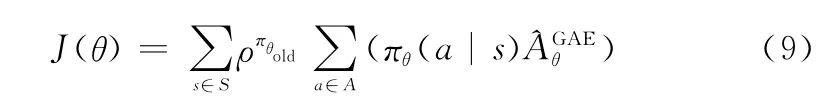
当执行强化学习异策略算法或同策略并行异步算法时，用于产生样本的行为策略β与所优化的目标策略π是不一致的。为了解决这种不一致性带来的误差，TRPO算法使用重要性权重πθ（a｜s）／β（a｜s）对此误差进行修正。可得到目标函数为

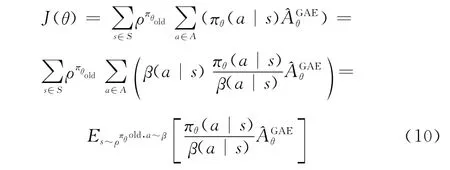
式中：θold为梯度更新前的参数。

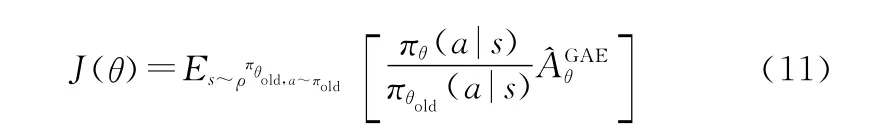
为了保证新旧策略间的差异不会太大，TRPO算法使用KL（Kullbck-Leible）散度来限制新旧策略分布之间的距离。因此，目标函数J（θ）优化时，需要满足如下限制：

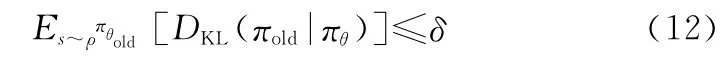
式中：δ为信赖域范围，用于限制两个策略分布之间的距离；DKL（πold｜πθ）为πold与πθ的KL散度。

求解目标函数时，可将目标约束转换为目标函数的一部分，目标函数转换为无目标约束的TRPO算法目标函数为

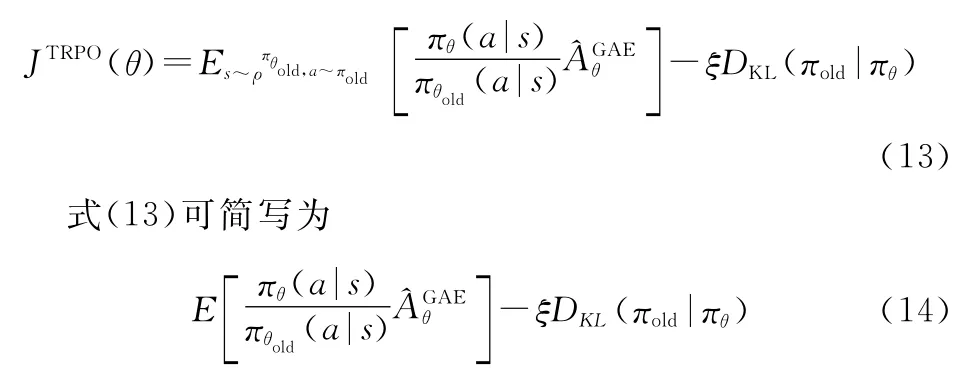
式中：ξ为约束项系数。

若在最大化JTRPO（θ）时不对θold和θ之间的距离加以限制，将会因为过大的参数更新幅度以及过大的策略比值而使得更新过程不稳定。令旧策略分布函数和新策略分布函数之间的比值为

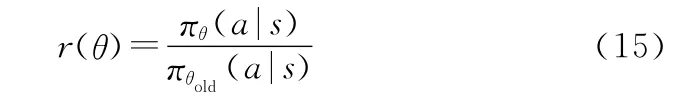
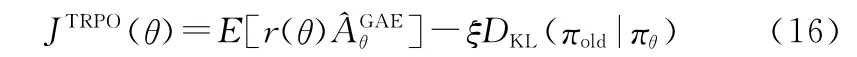
PPO算法通过使用一个截断的替代目标函数来优化TRPO算法，将r（θ）限定在1附近的领域中，即［1-ε，1＋ε］，来施加这一约束。其中，ε为超参数。采用clip限制方法的目标函数为

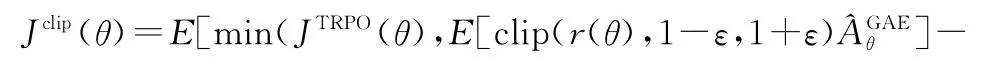
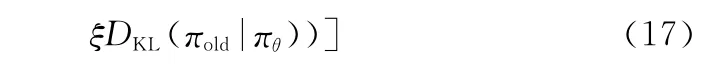
函数clip（r（θ），1-ε，1＋ε）将策略比值约束在［1-ε，1＋ε］范围内，可定义为

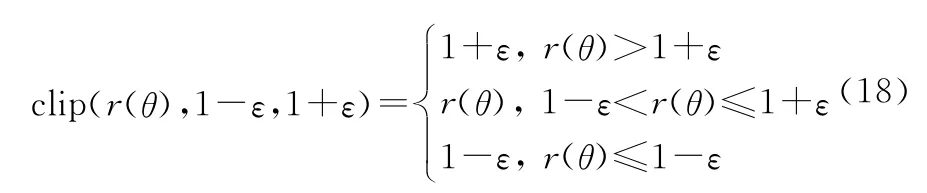
式中：ε为某一小量。

PPO算法的目标函数变为取原始值与截断值之间的较小值，这与TRPO算法尽可能最大化策略的更新幅度的理念不同，保证了策略迭代的稳定性。

将PPO算法应用在Actor-Critic网络结构上时，目标函数在截断回报的基础上增加关于值估计的误差项（Vθ（s）-Vtarget）和熵正则项H（s，πθ（·））用以鼓励探索。可得PPO目标函数为

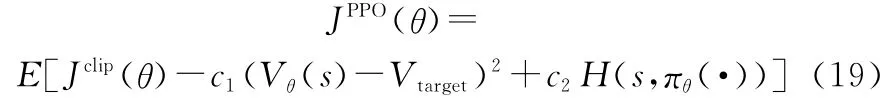
式中：c1为误差项参数；c2为熵正则项参数。

PPO算法流程［32］如下。

步骤1初始化策略网络πθ（s）的参数θ0，初始化价值网络的参数ϕ0。

步骤2遵循当前策略，智能体与环境交互得到当前系统状态｛st，at，rt｝。

步骤3使用优势估计函数方法计算优势值，并更新策略网络。其中，优势值计算公式为

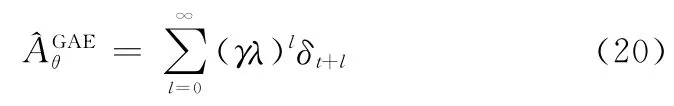
步骤4求解代理目标函数JPPO（θ）的梯度并更新参数θ，其中JPPO（θ）的表达式为

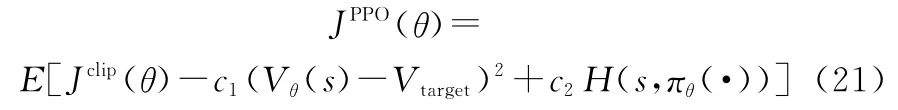
步骤5求解目标函数JBL（ϕ）的梯度并更新价值网络参数ϕ，其中JBL（ϕ）的表达式为

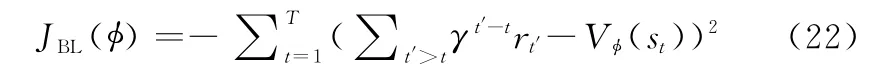
步骤6重复步骤2～步骤5，直到训练集到达终止状态。

2.2 深度强化学习离线训练方法

在深度强化学习离线训练算法中，将驾驶仪参数自整定问题建模为一个强化学习问题，需要定义出强化学习算法的状态、动作、奖励。其中，动作的定义比较明晰，即为驾驶仪设计参量二阶根自振频率ω，而状态与奖励函数需进一步讨论。

由于驾驶仪设计需根据特定飞行状态来进行设计，其中马赫数Ma、攻角α会影响气动特性变化，飞行高度H、马赫数Ma会影响动压变化。由此，可设置强化学习的状态向量为［H，Ma，α］T。对于特定飞行任务，H∈［Hmin，Hmax］，Ma∈［Mamin，Mamax］，α∈［αmin，αmax］。Hmin表示飞行最小高度，Hmax表示飞行最大高度；Mamin表示飞行最小马赫数，Mamax表示飞行最大马赫数；αmin表示飞行最小攻角，αmax表示飞行最大攻角。为使深度强化学习所使用的神经网络训练更快并消除输入数据的量纲，通常可对神经网络的输入输出进行归一化处理，使其尽量接近标准正态分布。定义神经输出的动作属于（-1，1）范围，并对于状态向量进行如下处理：

根据工程设计经验可取ω的范围为（0，ωmax），其中ωmax为最大自振频率，可得动作值的反归一化公式为

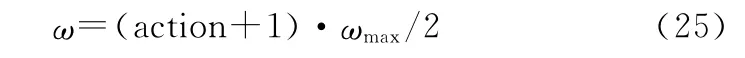
采用频域稳定裕度中的相位裕度P m和幅值裕度G m作为影响强化学习交互奖励的因素，可设置奖励函数为

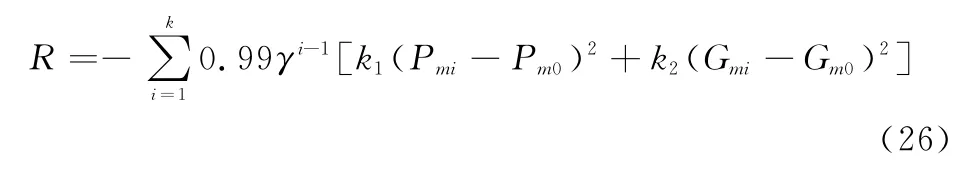
式中：γ为累积奖励的折扣因子；Pmi为每一训练步长产生的相位裕度；Pm0为理想相位裕度；Gmi为每一训练步长产生的幅值裕度；Gm0为理想幅值裕度；k1为相位裕度对奖励值的影响权重，k2为幅值裕度对奖励值的影响权重。每一步长产生的相位裕度和幅值裕度可由Matlab相关函数计算得到。

将状态空间、动作空间、奖励函数及智能体交互环境代入PPO算法框架中，可以得到基于PPO算法的驾驶仪参数自整定训练框架如图3所示。

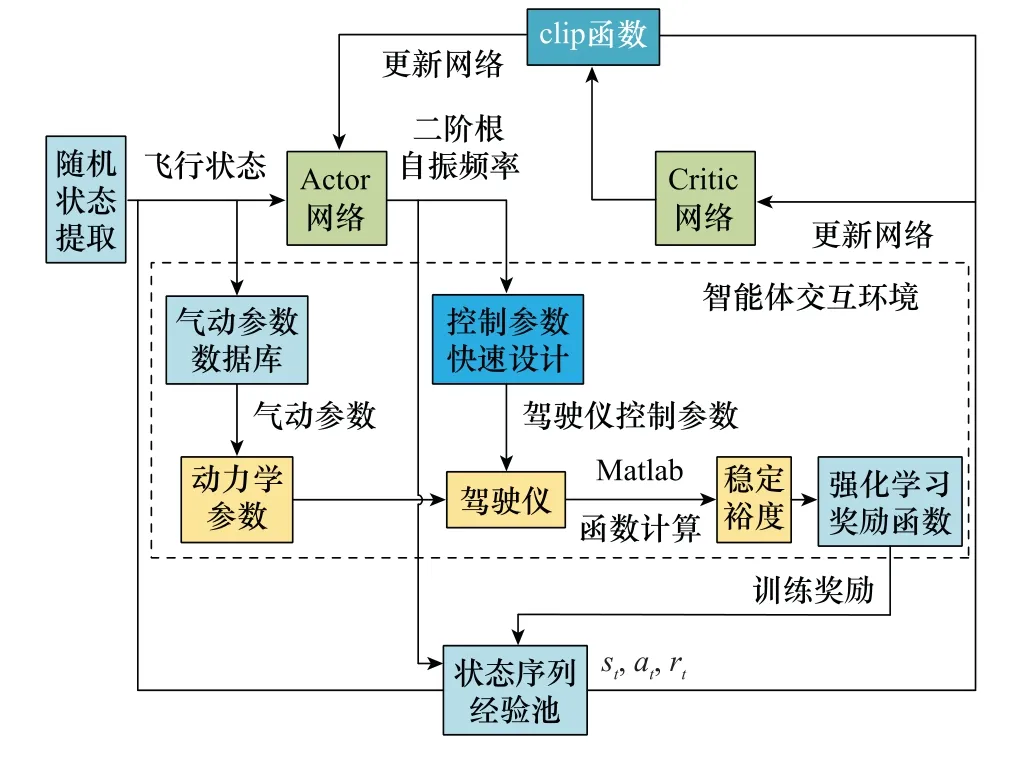
图3 基于PPO算法的参数自整定离线训练框架Fig.3 Parameter tuning training framework based on PPO algorithm

图3中Actor网络选用具有256个隐藏神经元的MLP神经网络，Critic网络选用具有256个隐藏神经元的MLP神经网络；st、at、rt分别为强化学习算法当前的状态值、动作值、奖励值；驾驶仪控制参数为k g、ωi、k ac。

2.3 控制参数在线实时计算策略

将训练完成的MLP神经网络进行在线部署，即根据当前实际的飞行状态（高度、马赫数、攻角），由MLP神经网络实时计算得到二阶根自振频率ω，并调用快速设计方法中的极点配置解析计算方程，从而得到驾驶仪控制参数k g、ωi、k ac，完成控制参数快速自适应调整。MLP神经网络在线实时计算模型如图4所示。

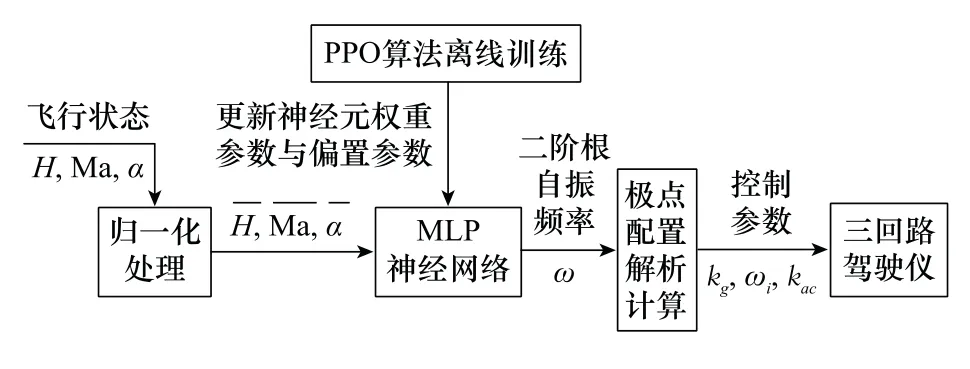
图4 MLP神经网络在线实时计算模型Fig.4 MLP neural network online real-time calculation model

图4中的MLP神经网络是由输入层、隐藏层及输出层构成的神经网络模型，其输入层神经元接收输入信号，隐藏层和输出层的每一个神经元与其相邻的所有神经元连接，即全连接，同一层的神经元间不相连。隐藏层和输出层中每一个神经元的输入为前一层所有神经元输出值的加权和。假设为MLP中第l层第m个神经元的输入值，和分别为该神经元输出值和偏置参数，为该神经元与第l-1层第i个神经元的权重参数，则有：

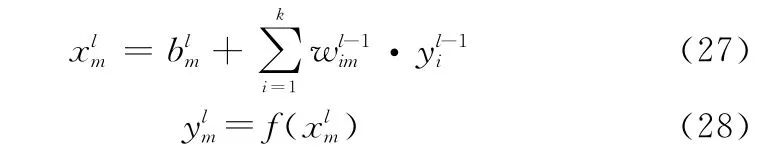
式中：f（·）为非线性激活函数分别为神经元权重参数和偏差参数，为强化学习算法训练所得。非线性激活函数选用线性整流函数（rectified linear unit，ReLU），函数图像如图5所示，表达式为

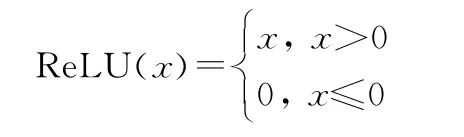
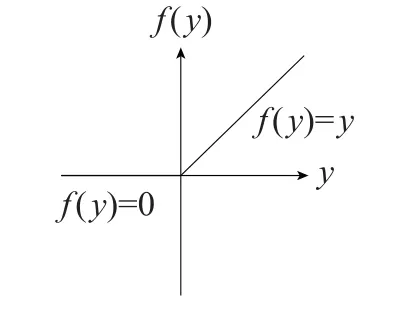
图5 Re LU函数Fig.5 Re LU function

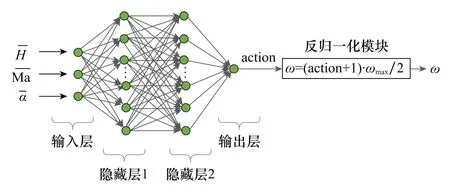
图6 MLP神经网络结构图Fig.6 MLP neural network structure diagram

由于使用飞行器全包络飞行状态数据对MLP神经网络进行训练，故该神经网络适用于飞行器全包络飞行过程，且MLP神经网络的非线性特征可对飞行过程中的参数不确定性有着一定的适应性。

3 仿真分析

本节将对驾驶仪参数自整定模型进行深度强化学习训练，给出了PPO算法训练的效果，并对加入MLP神经网络控制系统的飞行器典型指令跟踪及再入段轨迹跟踪进行仿真验证。

选取PPO 算法的状态空间为［H，Ma，α］，H∈［0，20-000］，Ma∈［0.8，4.5］，α∈［-5，8］。

选取设计指标为控制系统理想相位裕度P m0＝65°、理想幅值裕度Gm0＝8.5 dB，取奖励函数为

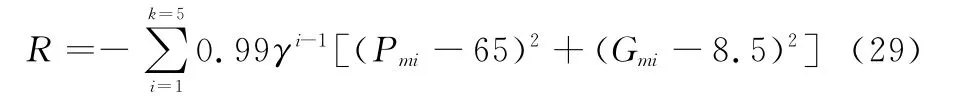
对PPO算法训练超参数进行预调试，调试得到PPO算法训练的超参数如表1所示。

表1 PPO算法训练超参数Table 1 Training hyperparameters of PPO algorithm

若按照强化学习方法工程应用常规思路，需选择影响驾驶仪状态的3个设计参数k g、ωi、kac作为智能体动作，进行三维动作空间训练，训练过程中的奖励值变化如图7所示。

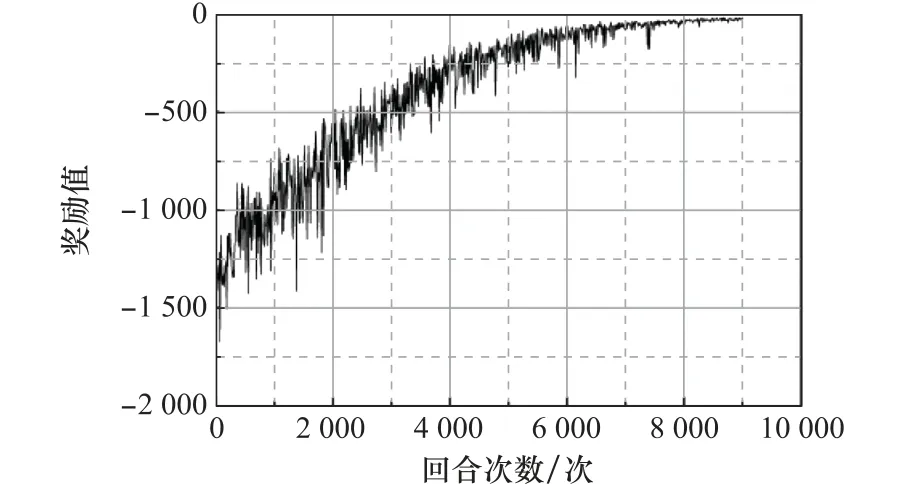
图7 三维动作训练过程奖励值变化曲线Fig.7 Three-dimensional actions training process reward value curve

本文利用已有的研究对象模型转换方法，对强化学习训练进行适当简化，采用一维动作ω进行训练。训练过程中奖励值的变化如图8所示，可以看出在训练初期由于动作随机选取使得奖励很小，随着训练的进行，智能体选取能产生较大奖励动作的概率逐渐增大，使得训练回合奖励值逐渐增大，并逐渐收敛。通过降低动作空间维数，可有效提高深度强化学习算法的效率和奖励函数收敛性。

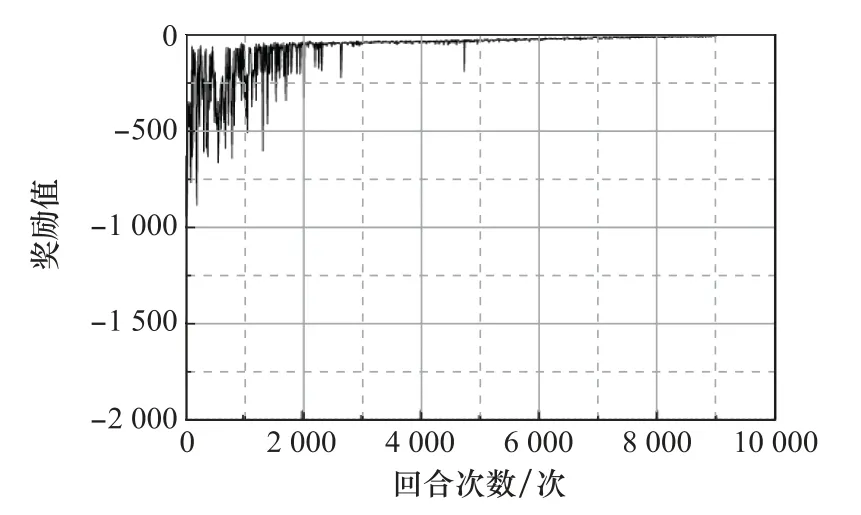
图8 一维动作训练过程奖励值变化曲线Fig.8 One-dimensional action training process reward value curve

训练得到以飞行状态为输入、以驾驶仪设计参量为输出的MLP神经网络，该神经网络适用于飞行器全包络飞行状态。取某飞行器再入段进行仿真验证，其高度变化曲线如图9所示，马赫数变化曲线如图10所示，攻角变化曲线如图11所示。

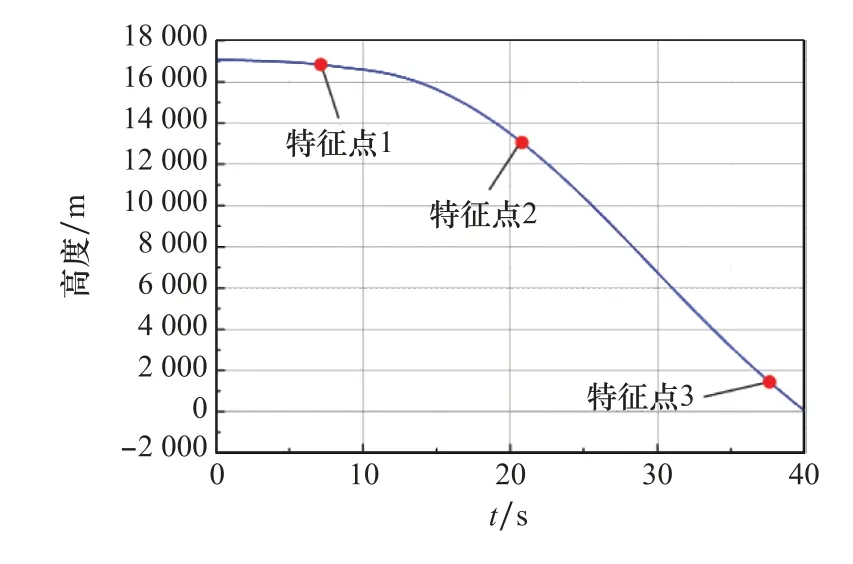
图9 再入段高度变化曲线Fig.9 Reentry height curve

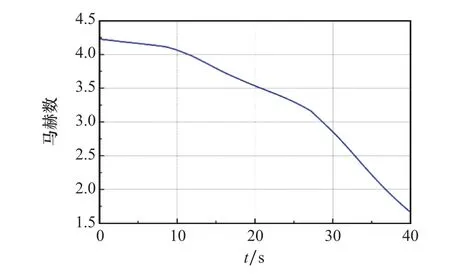
图10 再入段马赫数变化曲线Fig.10 Reentry Mach number curve

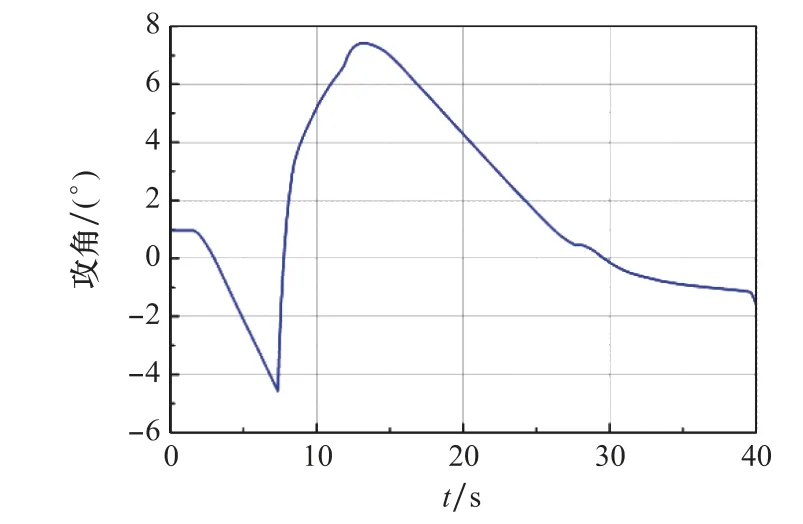
图11 再入段攻角变化曲线Fig.11 Reentry angle attack curve

选取飞行过程特征点如图9所示，特征点飞行状态如表2所示。取舵机参数：ωact＝220 rad／s，μact＝0.65；陀螺参数ωgyro＝400 rad／s，μgyro＝0.65；加速度计参数ωacce＝300 rad／s，μacce＝0.65；结构滤波器参数ωsf＝314 rad／s，μsf＝0.5；其他参数取c＝0.68 m。

表2 不同特征点处的飞行状态Table 2 Flight status at different feature points

取设计参数τ＝0.3，μ＝0.7，使用训练完成的MLP神经网络计算得到二阶根自振频率ω，表3给出了设计结果及设计得到的驾驶仪特性结果，可以看出驾驶仪开环稳定性和闭环特性满足设计要求。

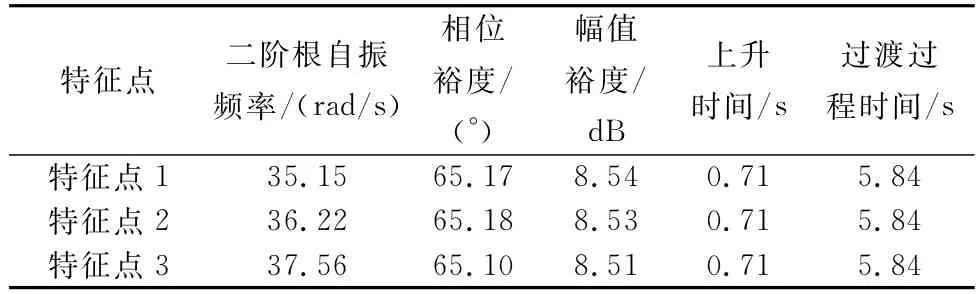
表3 不同飞行状态设计结果Table 3 Design results of different flight states

将计算结果代入三回路驾驶仪进行仿真，其单位阶跃响应曲线如图12所示，可以看出通过深度强化学习设计得到的三回路驾驶仪性能表现良好。

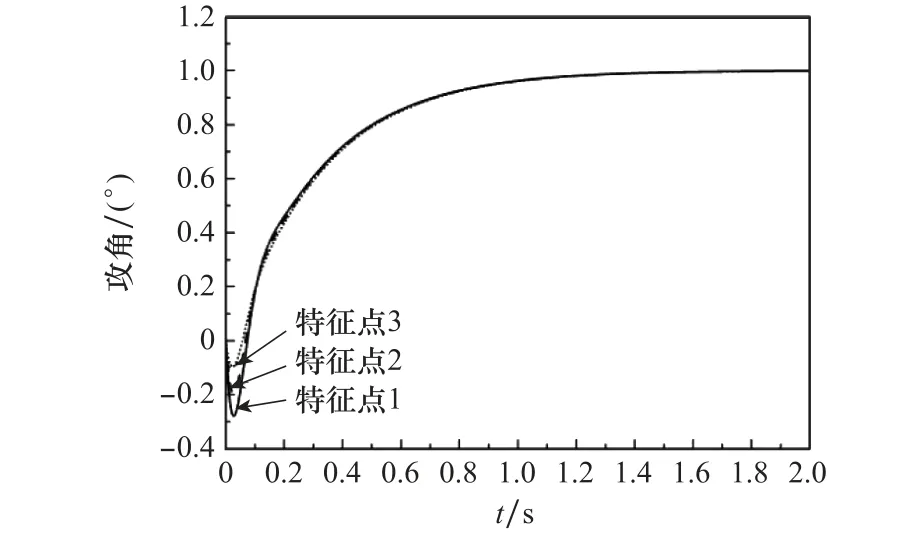
图12 基于深度强化学习参数自整定的驾驶仪响应曲线Fig.12 Response curve of autopilot based on deep reinforcement learning parameter tuning

为验证MLP神经网络对一定范围飞行状态的适用性，对飞行器全再入段进行仿真，其高度范围为［0 m，18-000 m］，马赫数范围为［1.5，4.5］，攻角范围为［-5°，8°］。将深度强化学习方法训练好的MLP神经网络部署到飞行器控制系统中，使飞行器在飞行过程中可以实时调用MLP神经网络输出的设计参量，进而快速得到驾驶仪三维控制参数，从而完成飞行器控制任务。俯仰通道过载指令与实际飞行过载如图13所示。

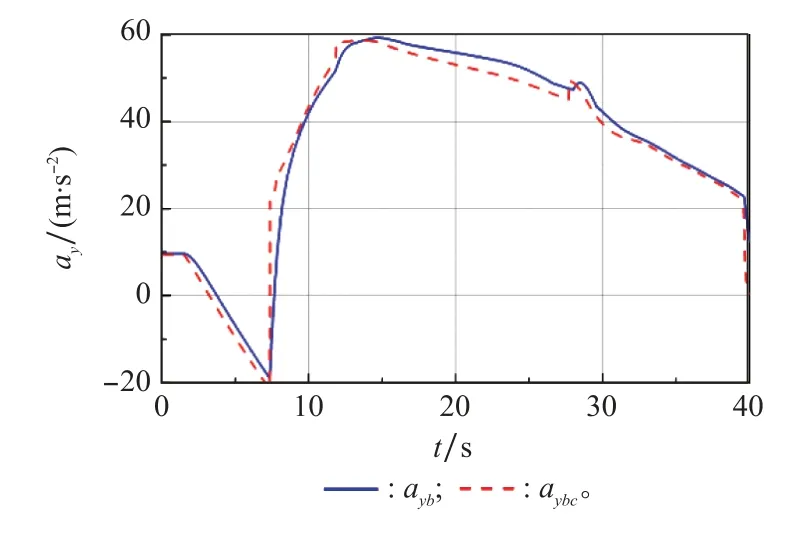
图13 俯仰通道指令跟踪曲线Fig.13 Command tracking curve of pitch channel

仿真结果表明，使用深度强化学习PPO算法训练得到的MLP神经网络，可以通过输入的状态向量［H，Ma，X c］T快速计算得出驾驶仪控制参数，指令跟踪误差在1.2%以内，飞行器可以很好地完成指令跟踪控制。飞行过程中MLP神经网络输出的驾驶仪设计参量二阶根自振频率ω如图14（a）所示，由快速自整定方法得到的驾驶仪控制参数k g、ωi、k ac如图14（b）～图14（d）所示，飞行过程中驾驶仪开环稳定裕度如图15所示。

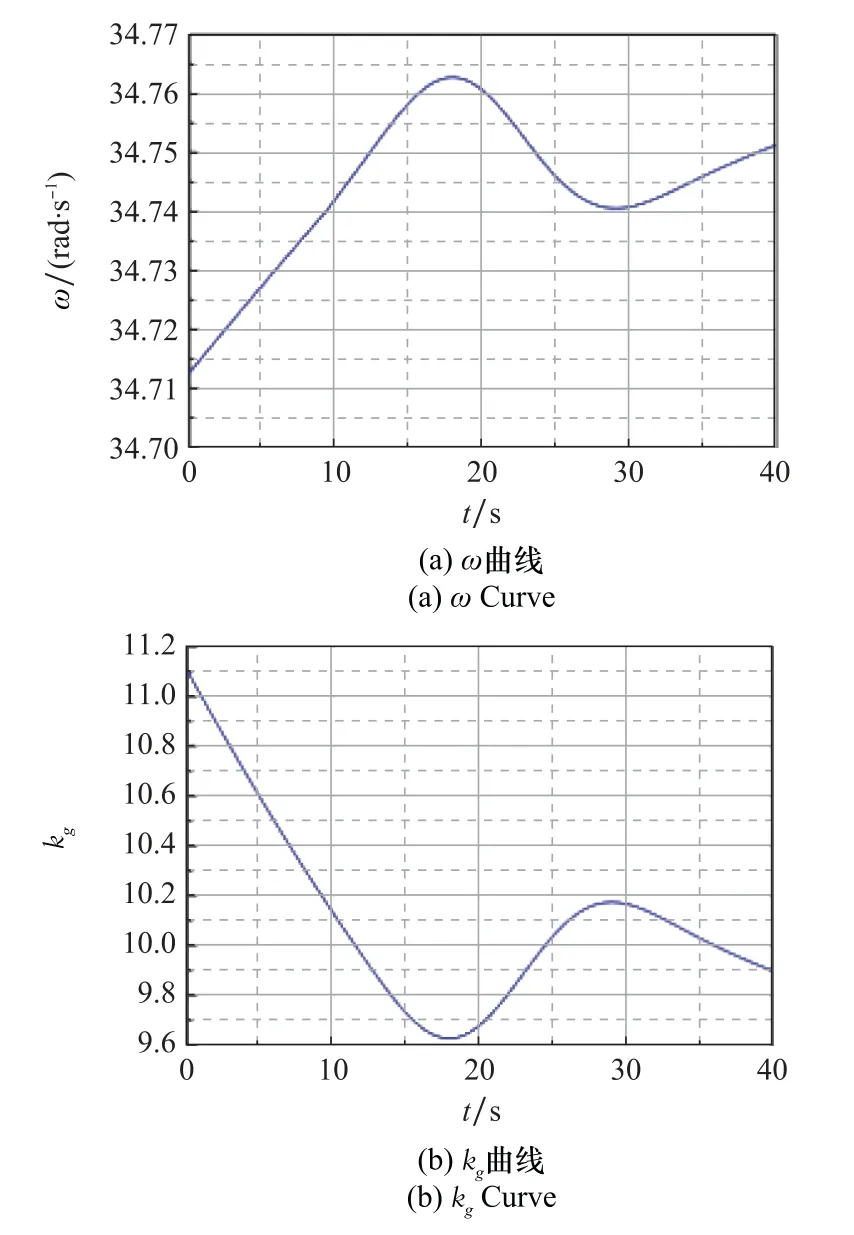
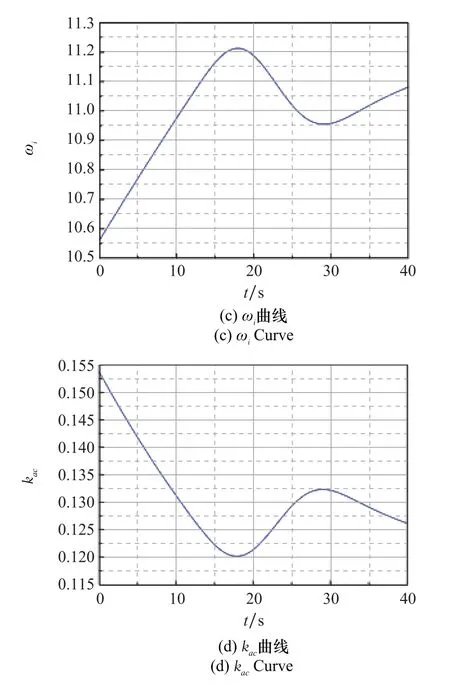
图14 神经网络输出及控制参数变化曲线Fig.14 Curves of neural network output and control parameters

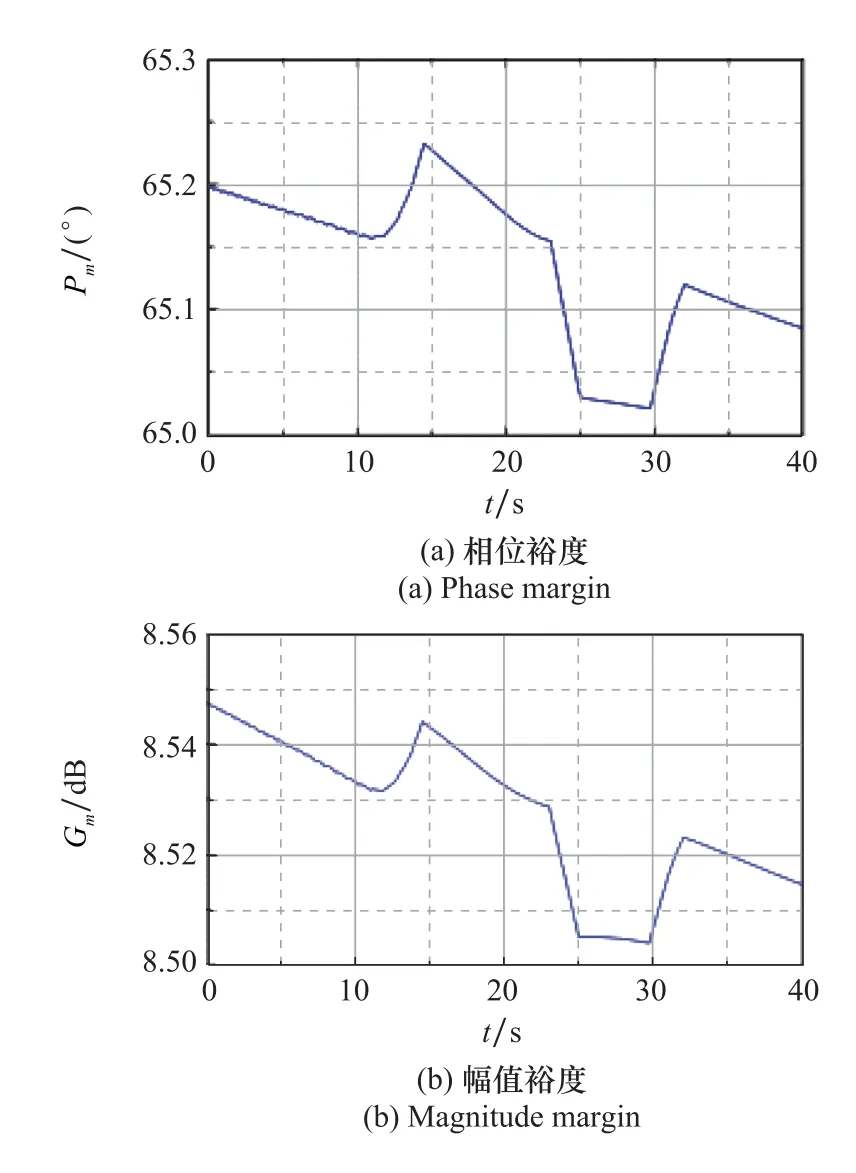
图15 稳定裕度变化曲线Fig.15 Stability margin curves

结果表明，以［H，Ma，α］T为输入、设计参量ω为输出的MLP神经网络具有很强的非线性特征，能够根据不同飞行状态得到不同的驾驶仪控制参数完成飞行任务，且驾驶仪稳定裕度满足设计要求，证明了基于深度强化学习的驾驶仪参数快速自整定方法的有效性。

4 结 论

本文针对深度强化学习对驾驶仪三维设计参数训练效率不高的问题，提出一种控制参数智能在线快速整定方法。首先，基于控制回路极点配置理论，提出可以应用于深度强化学习训练的控制参数快速设计方法，即由控制回路稳定性指标，通过少量计算即可快速得到对应的控制参数，从中提炼出完成参数快速设计所需的关键设计参量。其次，以快速设计方法为核心，选取影响飞行器气动特性变化主要参量，如高度、马赫数、攻角，构建面向飞行器全飞行包络范围的离线深度强化学习训练模块。采用近端策略优化算法，并从奖励函数设计、状态空间归一化、动作空间归一化3个方面进行优化设计，使得可以快速完成对设计参量调节MLP神经网络的训练。最后，将训练完成的MLP神经网络进行在线部署，即根据当前实际的飞行状态实时进行驾驶仪设计参量计算，对飞行器典型指令跟踪及再入段轨迹跟踪进行仿真验证。仿真结果表明，深度强化学习训练得到的驾驶仪对标称轨迹和扰动情况都具有良好的控制跟踪效果。