基于频谱旋转ωk算法的大斜视SAR地面动目标成像

熊世超，倪嘉成，*，张 群，2，罗 迎，2

（1.空军工程大学信息与导航学院，陕西 西安 710077；2.复旦大学波散射与遥感信息国家教育部重点实验室，上海 200433）

0 引 言

地面动目标成像（ground moving target imaging，GMTIm）是合成孔径雷达（synthetic aperture radar，SAR）成像中一个重要的问题。地面目标运动产生的多普勒频移导致动目标在方位向上偏移真实位置，动目标的距离向加速度和方位向运动使方位向调频率改变。同时，动目标与静止目标的距离单元移动也有很大区别，因此适用于静止目标的传统SAR成像方法难以对动目标聚焦成像［1-2］。

动目标成像方法可以分为特显点追踪类［3］、变换类、优化方法类、感兴趣区域（region of interest，ROI）类等。变换类的动目标成像方法包括基于Keystone变换的方法［2，4-5］和基于时频变换的方法［6-9］。文献［5］提出的多普勒Keystone变换方法能够高效地校正动目标的距离徙动，在高信杂比条件下实现动目标成像。优化方法类成像方法的主要思想是将动目标成像转化成一个优化问题，通过求解优化问题得到动目标的聚焦像［10-14］。由于散焦的动目标只存在于场景中很小的范围内，所以可以提取包含动目标全部信息的ROI数据后再进行动目标聚焦［15-17］，可降低后续处理的数据量，同时起到了抑制杂波的作用。文献［17］在ROI数据的基础上运用参数化稀疏表征的方法求解相位补偿函数，避免了速度的二维搜索，提升了参数搜索速度、增强了成像质量。然而，上述研究工作并没有考虑斜视的情况，斜视情况下的动目标成像主要面临以下问题：一是斜视带来的高阶相位误差不能忽略，不精确的斜距表达式不仅会加剧高阶相位误差所造成的影响，而且会导致动目标的参数估计不准，造成动目标聚焦困难；二是动目标的速度和雷达斜视角加剧了距离徙动效应和多普勒中心偏移，导致目标的成像结果几何形变严重，成像质量变差；三是利用匹配滤波类成像算法都存在十字旁瓣较大的问题，斜视动目标成像的聚焦困难和几何形变，导致在斜视成像中十字旁瓣问题更严重；四是在脉冲重复频率（pulse repetition frequency，PRF）不高的情况下，存在多普勒中心模糊和多普勒频谱混叠现象，导致成像结果散焦。研究斜视SAR成像的文献较多，包括从信号模型出发消除距离向方位向严重耦合的方法［18-19］和从成像模型出发提出新的等效几何模型的方法［20-21］。目前对于斜视SAR动目标成像的研究工作不多，文献［22-23］主要研究斜视条件下多通道SAR系统的地面运动目标检测（ground moving target indication，GMTI）。文献［24］提出了基于Keystone变换的三阶距离模型，解决了斜距模型不够精确的问题，利用先验信息预处理方法减轻了多普勒混叠问题和距离徙动效应，对于小斜视角的动目标成像有较好的效果。文献［25］通过修正的调频傅里叶变换（Fourier transform，FT）进行动目标粗聚焦，结合联合像素模型精准估计动目标径向速度，利用多通道SAR实现大斜视条件下SAR-GMTIm。

针对大斜视条件下SAR-GMTI存在的聚焦困难、几何形变严重、十字旁瓣大等问题，本文提出一种基于频谱旋转ωk算法的大斜视动目标成像方法。首先，推导了精确斜距条件下的斜视SAR动目标回波二维频域信号，使用ωk算法得到初步成像结果后提取动目标的ROI数据。在此基础上，通过基于二分搜索的最小化图像熵方法寻找动目标信号中未知参数的最佳值，并对提取的动目标ROI数据进行相位补偿，完成大斜视动目标的聚焦。然后，将信号重新变换到二维频域，通过频谱旋转方法［26-27］将大斜视的频谱形式变为正侧视的频谱形式，在实现频谱利用最大化、提高成像质量的同时，消除了成像几何形变。最后，考虑动目标的空域稀疏特性，利用迭代阈值算法对成像结果进行稀疏增强，抑制了旁瓣。所提方法能够实现斜视角大于等于70°条件下的动目标成像，仿真实验验证了所提方法的有效性。

1 大斜视动目标信号模型

在斜视条件下，载机平台与地面动目标之间的几何关系如图1所示，x轴是方位向，r轴是距离向。假设载机平台以速度v沿方位向直线飞行，高度为H，波束斜视角在地面投影的角度为θ。动目标的方位向速度和距离向速度分别为v x和v r。发射第n个脉冲的时刻为慢时间t s＝n T，T是脉冲重复间隔，当ts＝0时，波束中心与目标所在的直线交于A点，载机的地面投影与A点的视线距离为r0，在距A点x0的位置有一个动目标B，则载机平台和动目标的坐标分别为（0，0，H）和（x0＋r0sinθ，r1，0）。在ts时刻，载机平台的位置为（vts，0，H），动目标的位置为（x0＋r0sinθ＋v xt s，r1＋v rt s，0）。

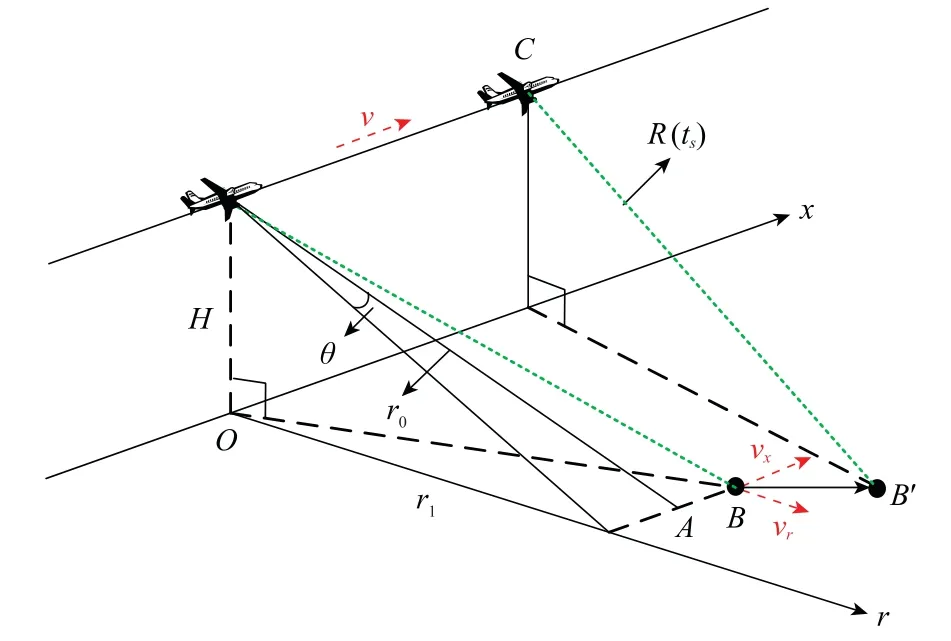
图1 斜视动目标成像几何模型Fig.1 Geometry model of squint mode moving targets imaging

雷达与动目标之间的瞬时斜距为

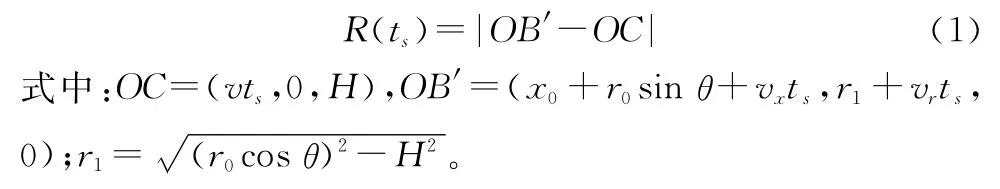
假设雷达发射线性调频信号，则基频回波为

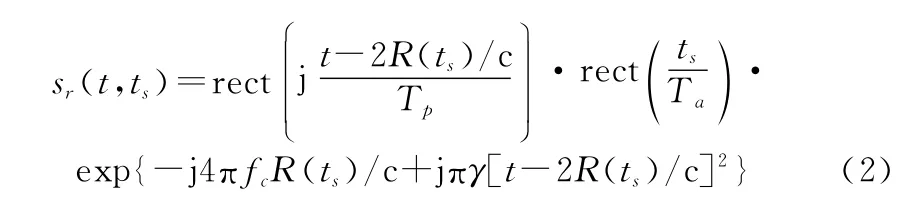
式中：rect（·）为矩形窗函数；t为快时间；Tp为脉冲宽度；Ta为合成孔径时间；f c为载波频率；γ为发射信号调频率；c为光速；目标散射系数为1。为了推导回波的二维频域表达式，首先对sr（t，ts）进行距离向FT，得到距离频域、方位时域的回波信号为

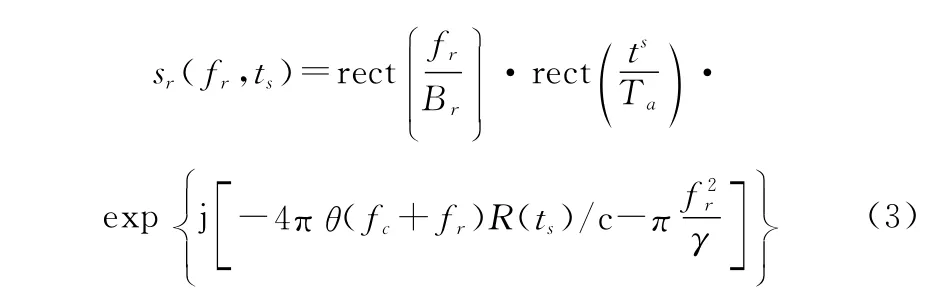
然后对sr（f r，ts）进行方位向FT，得到

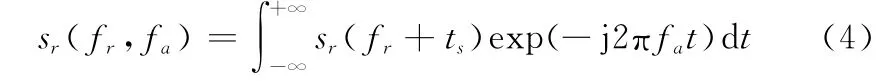
式中：f r和f a分别为距离频率和方位频率。运用驻定相位法可以得到二维频域表达式：

W r和W a分别为距离向和方位向的包络函数。根据ωk算法［28-29］，首先要进行一致压缩操作，斜视的一致压缩参考函数为

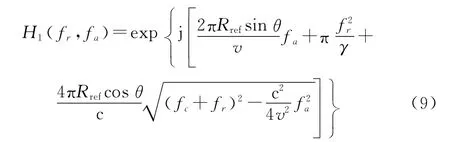
式中：Rref为参考距离。式（5）与式（9）相乘之后得到

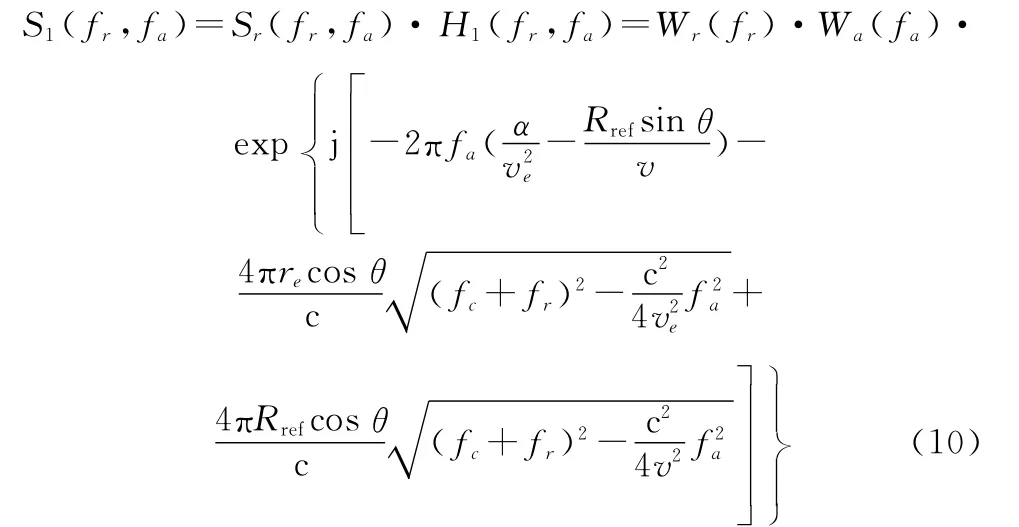
此时，直接进行二维逆FT（inverse FT，IFT）之后可以成像，但受到残余相位的影响，不同位置、不同速度的目标点存在不同的散焦情况。对于静止目标来说，目标点与参考点之间的距离越大，一致压缩之后的残余相位就越大，散焦越严重。对于动目标而言，式（10）的第二个相位项包含与动目标未知速度有关的re和v e，除了动目标与参考点的距离外，动目标的速度也会影响聚焦。距离引起的散焦可由后续的精确Stolt插值来消除，而速度引起的散焦则需要通过补偿速度产生的残余相位来解决。对式（10）进行二维IFT得到散焦的动目标成像结果，提取包含动目标的ROI数据，在此基础上进行后续的动目标聚焦，能够降低数据量，同时不丢失动目标信息，而且能够在动目标聚焦的过程中抑制背景杂波。对于多普勒模糊问题，很多文献提出了成熟的解决方法［2，30-31］，通过提高PRF也能避免多普勒模糊，本文算法假设在没有多普勒模糊的情况下进行动目标聚焦。

2 大斜视动目标成像方法

如图2所示，所提的大斜视动目标成像方法包括ROI数据提取、参数估计和聚焦成像3个部分。ROI数据提取是在初步成像结果中截取包含散焦动目标的区域，参数估计部分主要通过基于二分搜索的最小化图像熵方法，完成动目标信号中未知参数的估计。最后利用估计的参数进行动目标的聚焦成像。

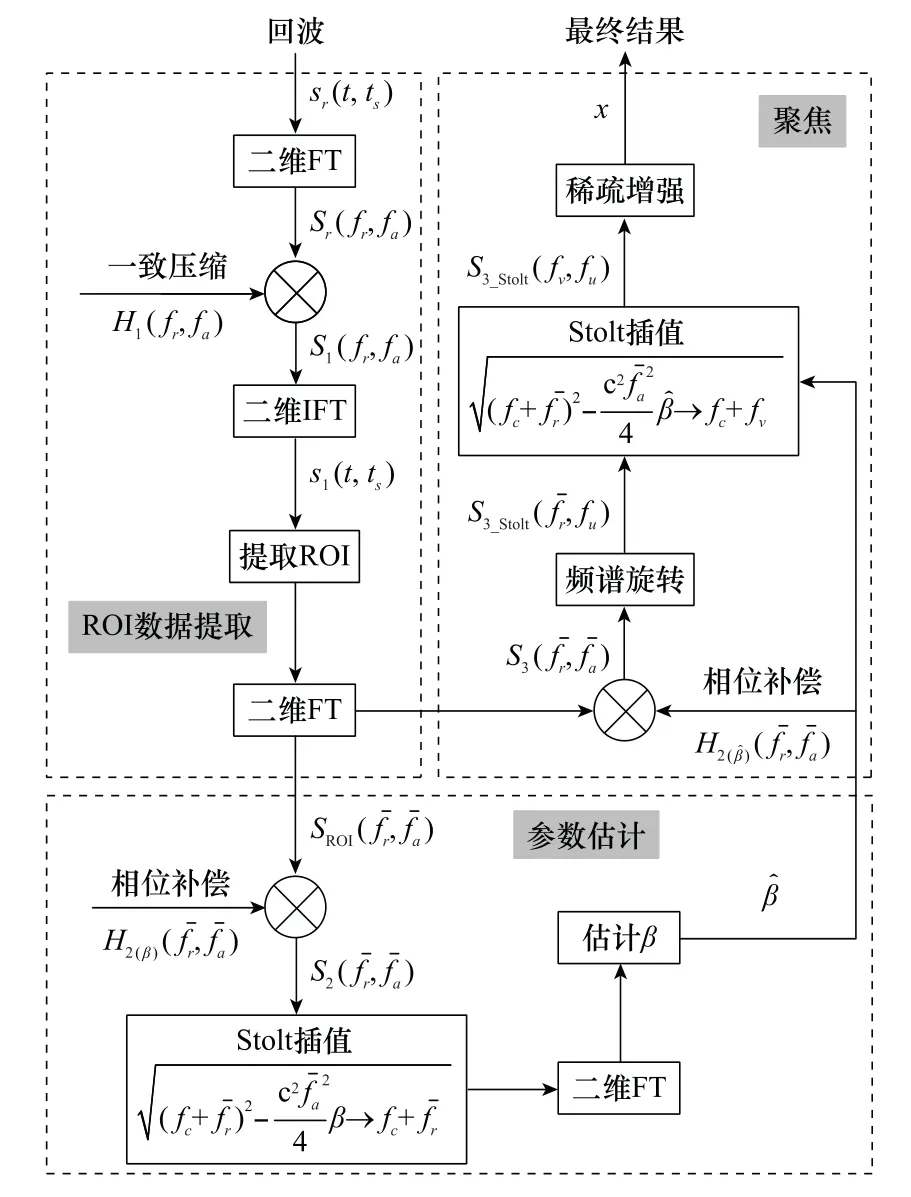
图2 算法流程图Fig.2 Algorithm flow chart

2.1 参数估计

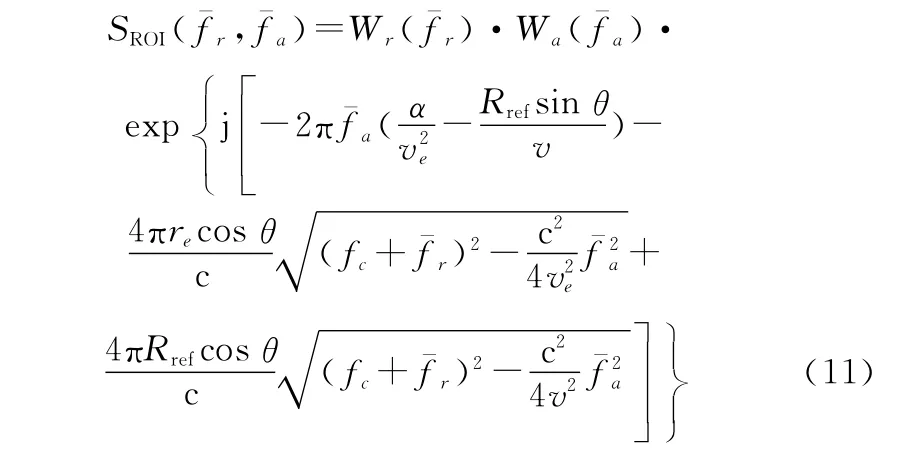
设置β的初始值为＝1／v2，利用其构造相位补偿函数：

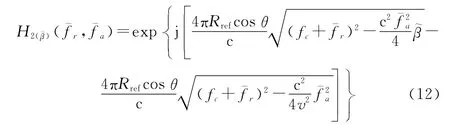
将ROI数据与相位补偿函数相乘，即式（12）与式（11）相乘得到

为了消除残余相位，还需要按式（14）对式（13）进行Stolt插值，得到

当≠β时，由于第二项残余相位的存在，在进行FT后图像依然是散焦的；当＝β时，式（15）变为

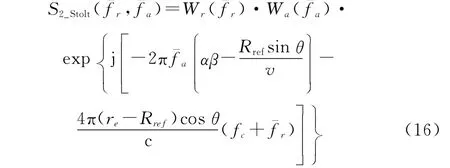
对其进行二维IFT可得到聚焦的图像，利用聚焦图像具有最小图像熵的特性，通过迭代的方式可以估计出最佳的，估计算法如下。

2.2 基于频谱旋转的动目标聚焦

通过第2.1节的方法估计出参数之后，可根据估计出的构造相位补偿函数：

此时，对式（18）Stolt插值后进行二维IFT，即能得到动目标的聚焦像，然而插值操作需要选择矩形的频谱支撑区域，随着斜视角增大，频谱支撑区域变小。在斜视角为45°时，如图3（a）所示，频谱支撑区域达到最小，之后随着斜视角的增大，频谱支撑区域逐渐增大。矩形区域越小，对成像质量的影响越大，除此之外，直接对大斜视条件下的二维频谱进行IFT得到的动目标聚焦结果还存在着几何形变，

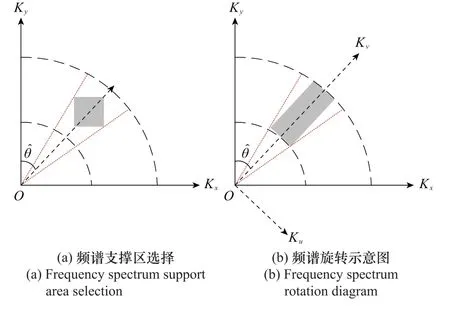
图3 频谱支撑区选择以及频谱旋转示意图Fig.3 Frequency spectrum support area selection and frequency spectrum rotation diagram

针对动目标聚焦的几何形变问题，设计了一种旋转角度为等效斜视角的频谱旋转方法，如图3（b）所示。将斜视的二维频谱旋转为正侧视的频谱形式，实现了矩形频谱区域最大化，同时消除了几何形变。图3（b）中，。

频谱旋转的角度与多普勒谱中心的偏移有关。图4为简化的动目标成像几何模型，斜视条件下的动目标，其回波信号的fdc可以分为两部分，包括载机平台速度造成的多普勒中心偏移fdc1和地面动目标速度造成的多普勒中心偏移fdc2。

图4 多普勒中心分析示意图Fig.4 Doppler centroid analysis diagram

由图4可以得到fdc1＝（2vsinθ）／λ与fdc2＝2（v xsinθ＋vrcosθ）／λ，fdc与二者之间的关系为fdc＝fdc1-fdc2。则频谱旋转的角度为

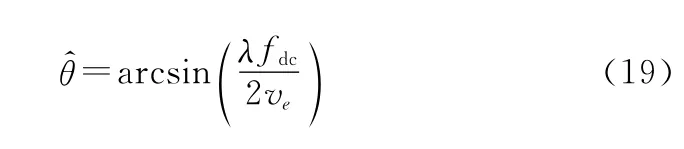
即图3中所显示的称之为等效斜视角。当目标速度v x＝0，v r＝0时,＝θ，斜视条件下频谱旋转的角度即为雷达系统斜视角，当目标速度不为0时，斜视条件下频谱旋转的角度为等效斜视角。由于非合作目标的速度是未知的，所以多普勒中心频谱不能通过fdc＝fdc1-fdc2计算得到，而要在回波信号的基础上通过多谱勒中心估计得到。

综上所述，频谱旋转因子为

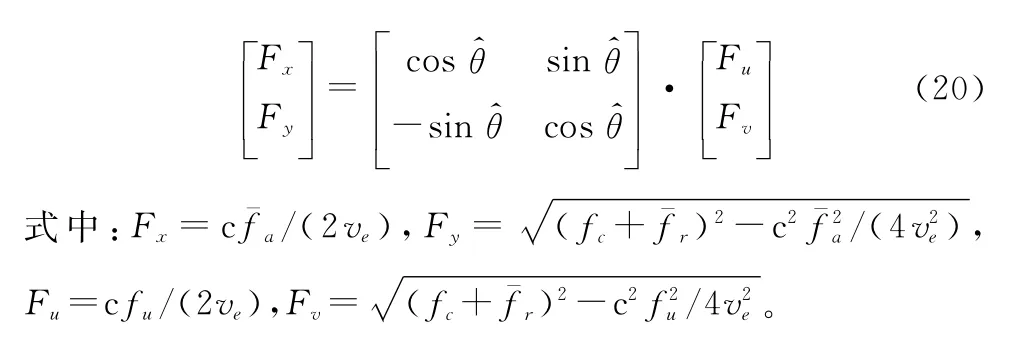
用方位向插值来完成频谱旋转操作，插值因子为

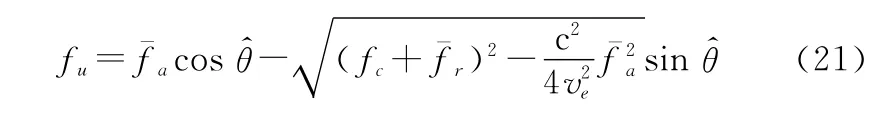
频谱旋转后，式（18）变为

此时直接对式（26）进行二维IFT即可得到聚焦的、无几何形变的动目标像。进一步，考虑到动目标在空域具有稀疏特性，如果对动目标聚焦像加以稀疏约束，运用稀疏重构的方法替代二维IFT则可以进一步抑制旁瓣。求解动目标稀疏解的过程可以表示为无约束L1范数优化问题：

式中：F a和F r分别为方位向和距离向FT矩阵；X为动目标稀疏解。此优化问题可以利用迭代阈值算法（iterative thresholding algorithm，ITA）进行求解，得到每一次迭代的稀疏解：

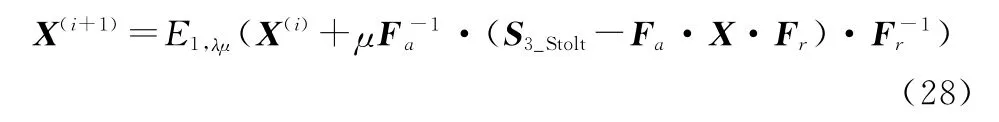
式中：μ是控制迭代收敛速度的参数；分别为方位向和距离向IFT；E1，λμ表示阈值算子：

对于全采样数据来说，只需进行一次迭代即可得到稀疏解，设稀疏解X初始化为0，则稀疏增强的算法流程如图5所示。

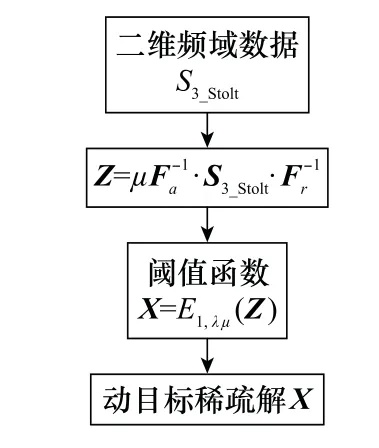
图5 稀疏增强算法流程图Fig.5 Sparse enhancement algorithm flow chart

3 实验验证

实验设置点目标和面目标两种仿真场景，散射点几何分布如图6所示，图6（a）的点目标场景含有两个动目标，P1在场景中心，P2距场景中心200 m；图6（b）的面目标场景为模拟的真实车辆，尺寸为6 m×6 m。

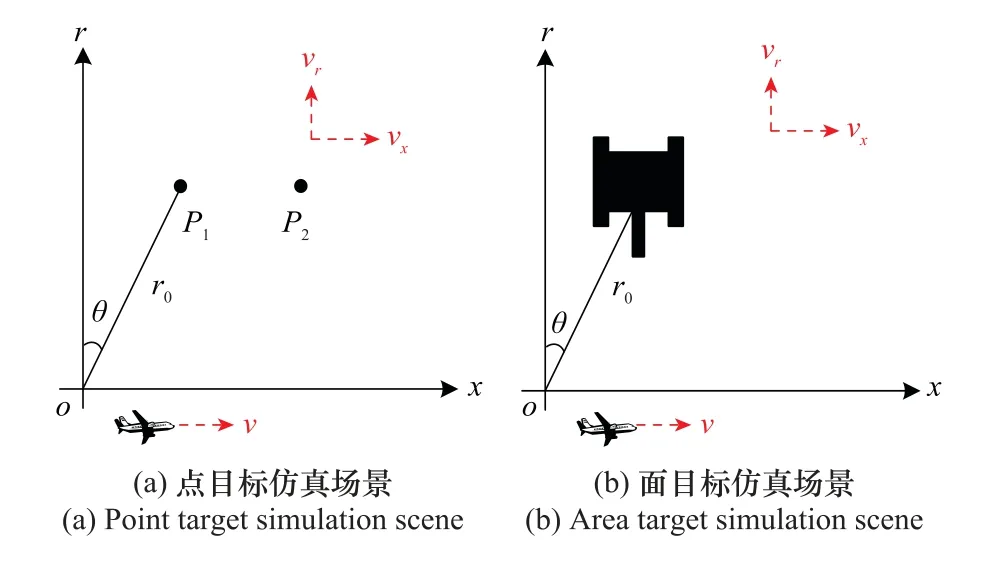
图6 实验仿真场景Fig.6 Experiment simulation scene

3.1 点目标实验

雷达仿真参数如下，载频为10 GHz，天线孔径为4 m，信号带宽为75 M Hz，信号脉宽为2.2μs，PRF为1 275 Hz，场景中心与航线最近距离为5 000 m，斜视角为70°，载机平台速度为150 m／s。实验设置两组不同的速度［v x，v r］，分别为V1＝［10，20］，V2＝［20，20］。图7（a）和图7（c）显示了常规斜视ωk算法的成像结果，在没有进行相位补偿之前，动目标是散焦的，速度不同的两组动目标散焦程度不同，在位置偏移上也有所区别。用虚线框出的区域是将要提取的动目标ROI数据，后续的处理都在ROI数据的基础上进行。根据所提算法，将提取的ROI数据进行二维FT，转换到二维频域。随后进行参数估计，第一步根据先验缩小参数范围，地面上大部分动目标的速度都在［-40 m／s，40 m／s］之间，根据边界速度可以得到相应的β值，如表1所示。由此可以确定β的取值范围为［2.652 5×10-5，8.264 5×10-5］。

表1 参数的边界值Table 1 Boundary value of parameters

第二步使用参数估计算法得到如图7（b）和图7（d）所示的参数迭代图，两组速度对应的最佳β分别为5.22×10-5、6.06×10-5。

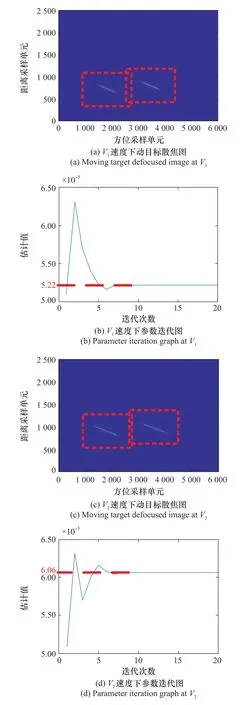
图7 两种速度下的动目标散焦图和参数迭代图Fig.7 Moving target defocused image and parameter iteration graph at V1 and V2

在动目标聚焦步骤设置对比实验，对比有无频谱旋转操作的成像效果。图8（a）和图8（c）为场景中心点P1分别在V1、V2速度下的无频谱旋转成像结果。图8（b）和图8（d）为场景边缘点P2分别在V1、V2速度下的无频谱旋转成像结果。图8（e）～图8（h）为相应的稀疏增强结果。使用估计出的参数β对动目标的未知运动参数进行补偿，不管动目标是场景中心点P1还是场景边缘点P2，都能在V1、V2两种速度下从散焦的长条形图像变为聚焦的图像。可以看到，无频谱旋转成像结果仍存在严重的几何形变，导致图8（e）～图8（h）的稀疏增强的结果也与真实点目标形状相差较大。图9（a）和图9（c）为场景中心点P1分别在V1、V2速度下的频谱旋转成像结果。图9（b）和图9（d）为场景边缘点P2分别在V1、V2速度下的频谱旋转成像结果。图9（e）～图9（h）为相应的稀疏增强结果。从实验结果看出，所提算法中的频谱旋转操作校正了散射点的几何形变，相应的稀疏增强效果更好。在V1、V2两种速度下，场景中心点P1和边缘点P2都能实现良好的聚焦成像。

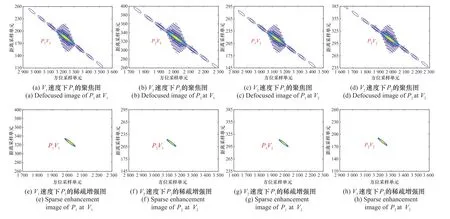
图8 无频谱旋转的动目标聚焦图和稀疏增强图Fig.8 Moving target focused images and sparse enhancement images without spectrum rotation

图9 有频谱旋转的动目标聚焦图和稀疏增强图Fig.9 Moving target focused images and sparse enhancement images with spectrum rotation

图10显示了两个散射点P1、P2在两个不同速度V1、V2下的方位向脉冲响应对比图，其中红虚线是无频谱旋转的聚焦结果，红实线是有频谱旋转的聚焦结果，蓝实线是频谱旋转加上稀疏增强的聚焦结果。频谱旋转后的点目标脉冲响应具有较窄的主瓣和较低的旁瓣，且稀疏增强进一步压缩了主瓣，压低了旁瓣。表2给出了两个散射点P1、P2在两个不同速度V1、V2下无频谱旋转和有频谱旋转的成像性能指标参数。对比可知，频谱旋转操作具有良好的聚焦性能，证明了本文算法的有效性。综上所述，点目标实验说明在70°斜视角的条件下，所提算法对于场景中心点、场景边缘点和不同的方位向、距离向速度，都能够实现良好的动目标聚焦。

图10 无频谱旋转、频谱旋转、频谱旋转＋稀疏增强的点目标能量方位剖面图Fig.10 Point target energy azimuth profile of no spectrum rotation，spectrum rotation，spectrum rotation plus sparse enhancement

表2 无频谱旋转和有频谱旋转的成像性能指标对比Table 2 Imaging performance index comparison between no spectrum rotation and spectrum rotation

3.2 面目标实验

面目标实验的仿真雷达参数如下，载频为10 GHz，天线孔径为1 m，信号带宽为300 M Hz，信号脉宽为2.2μs，PRF为1 275 Hz，场景中心与航线最近距离为5 000 m，斜视角为70°，载机平台速度为150 m／s。面目标的速度设置为［v x，v r］＝［30，20］，实际中车辆的运动不是简单的匀速直线运动，还有加速度的存在，所以设置了两组实验，第一组实验的动目标加速度为0，如图11所示。第二组实验的动目标加速度为［a x，ar］＝［0.5，1］，如图12所 示。图11（a）和图12（a）中用虚线矩形框框出了动目标的ROI数据，加速度的存在会影响动目标的散焦程度。图11（b）和图12（b）的参数估计显示有无加速度的参数β分别为7.16×10-5和5.28×10-5。根据估计出的参数对动目标进行相位补偿，得到动目标的聚焦图，如图11（c）和图12（c）所示。再经过稀疏增强步骤之后，得到图11（d）和图12（d）的结果，动目标的旁瓣被压低，得到了更好的聚焦结果。

图11 无加速度的面目标散焦图、参数迭代图、聚焦图和稀疏增强图Fig.11 Defocused image，parameter iteration graph，focused image and sparse enhancement image of area targets without acceleration

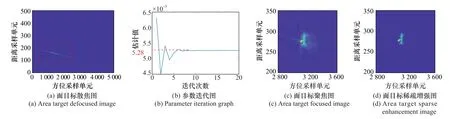
图12 有加速度的面目标散焦图、参数迭代图、聚焦图和稀疏增强图Fig.12 Defocused image，parameter iteration graph，focused image and sparse enhancement image of area targets with acceleration

由加速度带来的高阶相位误差会影响动目标的聚焦效果，从图12（c）中可以看出，有加速度的动目标的旁瓣增加，方位向左右旁瓣高度相差很大，这是由于所提方法的推导都是在无加速度的前提下进行的，斜距表达式为

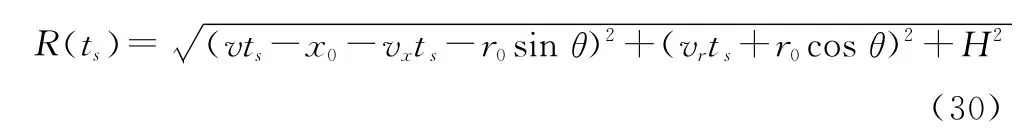
而有加速度时的斜距表达式为

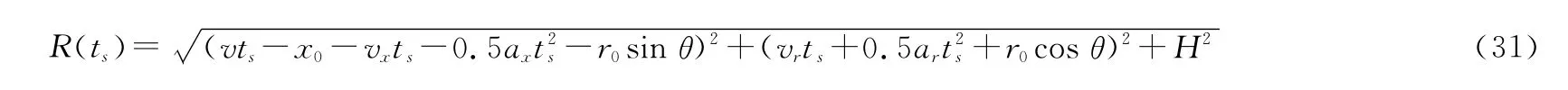
在用所提方法对有加速度的动目标进行聚焦的时候，会忽略掉关于慢时间ts的三阶及三阶以上的项，这就是高阶相位误差的来源。然而，只要加速度在一定范围内，动目标聚焦结果仍然是可接受的。面目标实验结果显示了在70°斜视角的条件下，所提算法对于无加速度和有一定加速度的情况都能够实现较好的动目标聚焦。

4 结 论

针对大斜视条件下的SAR-GMTI，提出了一种能够精确补偿地面运动目标未知参数的动目标成像算法，算法步骤主要有ROI数据提取、参数估计、相位补偿、频谱旋转和稀疏增强。使用无近似的斜距模型重新推导的斜视动目标ωk信号模型，能够进行精确的动目标相位补偿，从而实现动目标聚焦成像。ROI数据的提取能够降低后续处理的数据量，同时抑制除动目标以外的杂波，提高信杂比。参数估计步骤利用二分法对最小的图像熵进行搜索，实现最佳的参数估计，提高了搜索效率。频谱旋转步骤通过对二维频谱的旋转使矩形频谱最大化，提高成像质量的同时校正了几何形变。稀疏增强步骤则利用动目标在空域的稀疏性抑制了图像旁瓣。所提算法能够实现70°及以上斜视角条件下的SAR动目标成像。加速度的存在会产生高阶相位误差，因此大斜视条件下的高机动动目标成像将是下一步的研究方向。