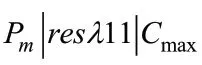遗传算法在车间调度中的研究

李志林

(浙江理工大学理学院，浙江 杭州 310000)

1 引言(Introduction)

工件的加工需要资源，资源也是优化目标的一个重要因素。资源的定义很广泛，例如加工工件所需的设备、员工、原材料等。我们把一般的资源，例如加工设备等统称为机器，把除了加工设备以外的其他资源称为额外资源。额外资源对调度的影响是多样化的，例如额外资源使用的数量往往可以决定工件的加工速度；额外资源有时需要不断损耗，有时又可以部分回收等。

遗传算法在函数优化、组合优化、生产调度以及机器学习领域有着广泛的应用。该算法基于对生物遗传和进化过程中选择、交叉、变异机理的模仿，来完成对问题最优解的自适应搜索过程。关于遗传算法在车间调度中的应用，陈金广等以最小化最大完工时间为优化目标，初始化时将种群规模扩大以增加种群多样性，同时使用新的适应度函数让染色体间更易区分。对于平行机调度的问题，孙超平研究了一类考虑外包的平行机调度问题，目标是使作业外包总成本与最大完工时间同时最小化。

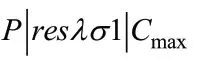
对于目标函数为极小化最大完工时间的有资源约束的平行机调度问题||，该问题已经在很多文献中进行了研究。特别地，当工件的加工时间均为单位时间时，GAREY等证明问题|⋅⋅⋅,p=1|在多项式时间()内可解；EDIS等在前人的基础上，介绍了在工件的加工时间都是单位时间的前提下，对于问题当工件具有到达时间情况下的模型|1⋅1,r ,p=1|、问题|，=1|和问题|1⋅1,p=1|∑C都是多项式时间可解的。

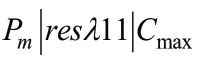
2 问题的符号介绍及相关描述(Symbol introduction of the problem and its related description)

2.1 的相关符号介绍

2.2 问题的相关描述

问题的可行性条件：设有可行解的目标函数值，为对于某一资源，在任意时刻∈[0,]，最多有1台机器正在使用。

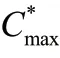
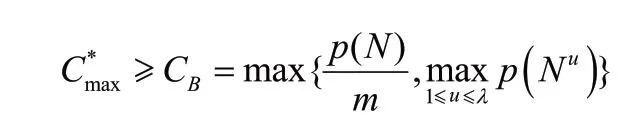
3 遗传算法的设计(Design of genetic algorithm)

遗传算法在函数优化、组合优化、生产调度以及机器学习领域有着广泛的应用。不同于其他调度问题，本文随机产生初始种群时，并不能够保证种群中的解是可行的，因此本文相对于其他遗传算法产生初始种群过程，多了可行性判定过程，初始种群的每个可行解都要满足本文资源约束的条件。这对于算法的运行时间有着重要的影响。同时在每次产生交叉种群与变异种群的过程中，也加入判别可行性的步骤，选取满足条件的解加入新种群，每次迭代，选取种群中最优的解进行输出。

通过上述性质可知，遗传算法以群体搜索为特性，优化结果与初始条件无关，这将使得优化结果更好。下面给出具体的遗传算法设计。

3.1 编码方式

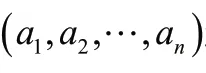
例如：对工件集合=(,,,,,,)，机器为,,的实例，如若其编码串表述如下：(1,2,1,2,3,1,3)，第一个数字1表示工件在第一台机器上的第一个位置，第二个数字2表示工件在第二台机器上的第一个位置，第三个数字1表示工件在第一台机器上的第二个位置，第四个数字2表示工件在第二台机器上的第二个位置加工，其他定义类似。则可知工件在机器上的顺序为(,,)，机器上加工顺序为(,)，机器上的顺序为(,)。

由此，编码表的定义已经说明完成，任意解根据编码都可以准确地刻画出其具体排序方式，方便问题求解。

3.2 初始种群的设计

遗传算法的初始种群采取随机生成原则。根据本文问题和编码的特点，采取如下产生初始种群方法。

对于个工件的集合，按照工件的顺序，对每个工件，在满足资源约束的条件下任意选取一台机器进行加工，本文设置初始种群为15 个可行解。可行解产生的方法如下所述。

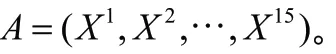
3.3 交叉变异以及选择策略的设计

交叉与变异运算是遗传算法的核心，它决定了算法的收敛速度以及优化结果。本文用目标函数值来衡量个体的适应度，针对本文的问题，目标函数为最小化最大完工时间min，即：目标函数越小，适应度越高。同时对于交叉变异个体的选取方式如下所述。

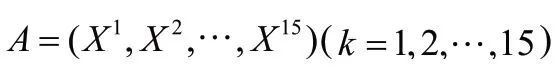
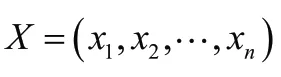
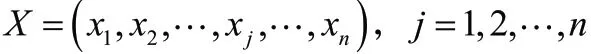
(4)遗传算子的选取。针对本文特点，交叉变异后的个体，并不一定能够满足本文的资源约束条件，则对交叉变异后的新个体，进行可行性判定，若满足可行性判定，则令其=，若不满足，则令其适应度的较大数值=10。由此来筛选下一代的个体，同时为了避免原种群较优的个体丢失，融合新旧种群，对种群中所有个体的适应度由小到大排序，选取适应度最优的前15 个个体作为下一次迭代的父代。

3.4 算法的具体设计

步骤1：参数初始化。设定种群规模=15,最大迭代次数，交叉概率 P和变异概率 P。

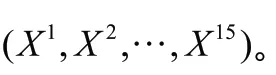
步骤4：同时对于步骤3产生的新个体，随机产生的变异概率P，判断其是否满足P＜0.1，若满足，则继续随机选取节点的方式进行单点变异，产生新的个体，加入种群；若无需交叉，直接加入新种群。

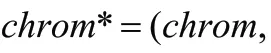
4 数值模拟及结果分析(Numerical simulation and result analysis)

采用数值计算的方式来验证所设计的遗传算法，算法采用了Python 3.10.1来实现算法和对数值实验的模拟，电脑的运行环境为Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz和8GB Ram。本文的数值模拟实例通过随机产生，分别对小规模实例和大规模实例进行分析，目的是更好地证明该算法的有效性。

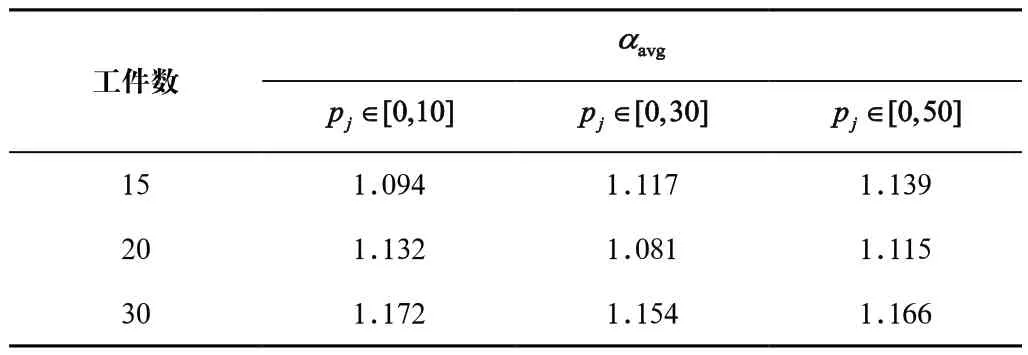
表1 小规模实例运行20 次的 αavg数据结果Tab.1 αavg data results of a small-scale instance running for 20 times

同样需要验证算法对大规模实例的效果。增加工件数为100，资源种类数为20，迭代次数为50进行分析。工件大小分别从[0,30]、[0,50]、[0,100]中随机取数的不同类型进行分析，每类问题中工件的大小随机产生20 个实例进行实验，对、和进行对比，可以看到，当工件个数和大小持续增加时，稳定在1.05以内，而最坏情况，也在1.2范围内，该遗传算法对于求解本文问题有着较好的优化作用。如表2所示。

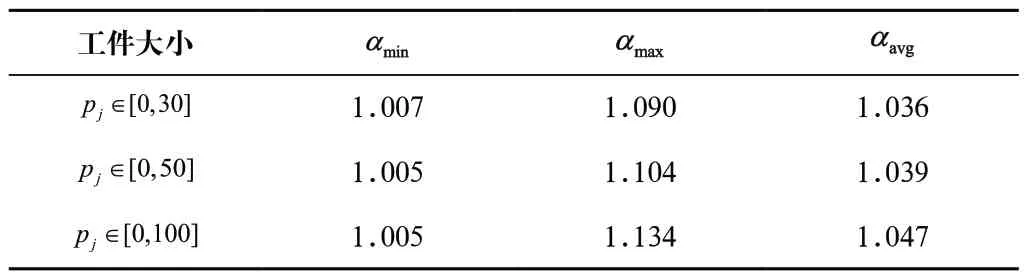
表2 100 个工件的实验结果Tab.2 Experimental results of 100 workpieces

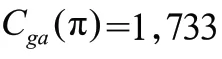
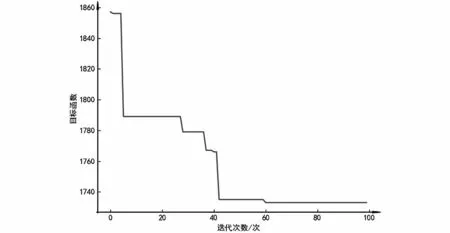
图1 遗传算法迭代收敛图Fig.1 Iterative convergence diagram of genetic algorithm

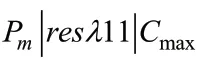
5 结论(Conclusion)