基于RBFNN-GA的纵封热封过程工艺参数决策方法研究

彭来湖，徐钦栋

(1.浙江理工大学，浙江 杭州 310000；2.浙江理工大学龙港研究院，浙江 温州 325000)

1 引言(Introduction)

随着包装行业的快速发展，对软包加工机械设备的智能化要求越来越高，其中枕式包装机在包装装备中发展最早，应用最广。虽然我国枕式包装机设备研发能力有了一定程度的发展，许多高校与研发机构也纷纷参与包装机械的研发工作，但是枕式包装机纵封热封加工过程依旧存在智能化不足、工艺参数选择效率低等问题。

对于纵封热封过程工艺参数的选择问题，国内外学者都对其进行了研究。AIYENGAR等与曹菲等在实验室条件下对三种类型的复合膜进行热封强度的测定，同时分析不同失效模式，通过不同的失效模式对数据进行分类，得出了简单的定性关系，但该方法缺少定量关系，难以应用到实际生产过程当中；杜玉宝在对复合膜进行热封强度测试后，通过数据进行二次多项式回归拟合，得出了工艺参数与热封强度的关系曲线，但应用到实际生产加工还需将实验工艺参数转换成实际工程参数。已有的研究工作缺少了实际生产的分析，同时未对热封强度多参数的情况寻找其最优解。

本文以热封强度作为生产质量的重要判定依据，并且考虑包装机在工作工程中受到复杂工艺的影响，进行枕式包装机工艺参数决策方法研究。首先对加工流程中的各个生产数据进行统计，其次通过RBF神经网络进行回归模型的训练，然后根据复合膜材料断裂屈服强度确定目标热封强度，最后通过遗传算法，迭代寻找最优结果。

2 包装机工艺分析(Process analysis of the packaging machine)

2.1 包装机热封流程

枕式包装机纵封结构，采用双平板热封结构，如图1所示，结构1、3为复合膜旋转挤压辊，通过主动旋转带动复合膜向前运动，同时会对复合膜产生相对恒定的压力；结构2为双板导热机构，以电生热方式控制双板间的温度达到设定温度。复合膜在结构1前旋转挤压辊的带动下向前运动，同时使复合膜内膜紧贴；结构2的双板之间存在一定的间隙，距离为，复合膜通过该间隙时高温使其预热融化；结构3后旋转挤压辊对预热后的复合膜内膜进行挤压贴合，达到热封效果，最后采用QBT 2358-1998标准进行热封强度的测定，单位为N/15mm。根据热封强度对热封效果进行判定。

图1 纵封热封机构Fig.1 Structure of longitudinal and heat sealing machine

在热封过程中，热封时间为纵封热封过程当中的重要影响因素，但在实际生产加工过程当中无法对热封时间进行精确设定。本文针对枕式包装机实际加工流程，通过热封速度来代替表示热封时间。热封速度的单位为包/min，与热封时间的关系如式(1)所示。

其中，为加热板长度，单位为mm，为复合膜长度，单位为mm。综上所述，在实际机床加工过程当中，对热封强度的主要影响因素包括双平板热封距离、热封温度和热封速度。

2.2 热封效果分析

枕式包装机产品的热封强度是对热封效果的一个重要判定因素，通常是测量复合膜材料热封处的力学性能进行判定。对复合膜材料进行热封处理后，对其进行纵向实验拉伸会产生四种不同情况。

如图2(a)所示为热封后复合膜状态，1处为热封层层间结合处，2为复合膜层间结合处；如图2(b)所示为复合膜内层断裂状态，当热封强度与复合膜层间结合强度相差较小时，复合膜层间发生断裂分离，此时热封效果较好；如图2(c)所示为热封失效状态，热封强度较低，复合膜层间结合强度远大于热封强度，此状态热封效果最差；如图2(d)所示为整体撕裂状态，当热封强度大于复合膜材料的断裂屈服强度时发生整体撕裂，此时虽然热封强度较大，但热封表面发生扭曲变形，其韧性与外观表面都无法达到要求，热封效果较差。综上所述，热封强度可以极大地反映出复合膜材料的热封效果。

图2 热封状态示意图Fig.2 Schematic diagram of heat sealing state

根据实际生产过程统计可知，合适的目标热封强度P与复合膜自身断裂的屈服强度P有关。经过实际加工结果统计估算，存在式(2)关系。当热封强度P满足式(2)关系，则认为其满足实际加工需求的热封强度。

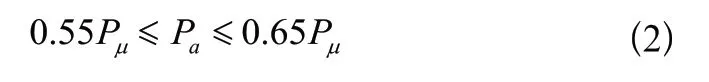
3 RBFNN-GA决策方法(RBFNN-GA decisionmaking method)

3.1 RBFNN-GA决策方法总体结构

决策方法模型设计结构图如图3所示，输入材料屈服强度计算目标热封强度，同时根据实际加工需求设定部分工艺参数作为约束条件；建立RBF神经网络回归模型并验证其准确性；将遗传算法迭代种群输入到回归模型中进行适应度计算；通过遗传算法进行寻优计算，得到热封强度与目标热封强度相近的最优工艺参数。

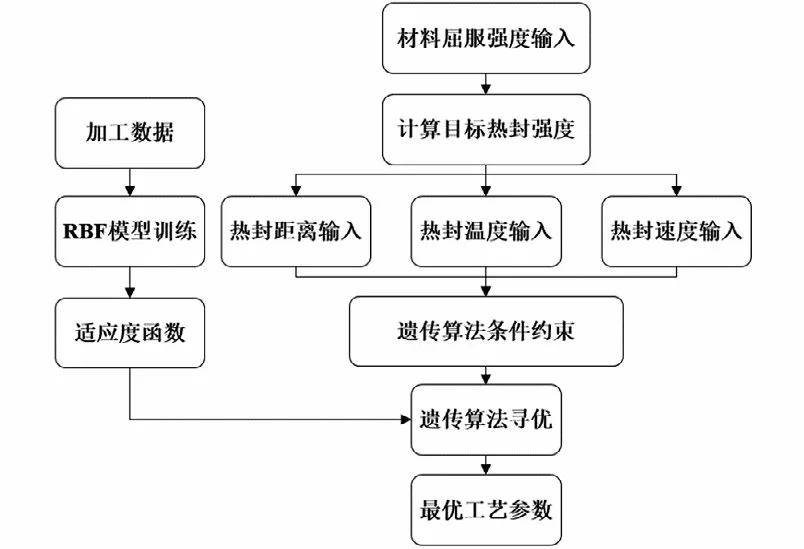
图3 决策方法结构图Fig.3 Structure diagram of decision-making method

3.2 RBF神经网络模型建立

在该决策方法中，对于热封材料的更换需要进行数据的重新迭代学习，在实际应用过程当中要求该网络具有较快的收敛性。对于RBF神经网络，只存在少数几个连接权值影响输出，具有较快的收敛性。

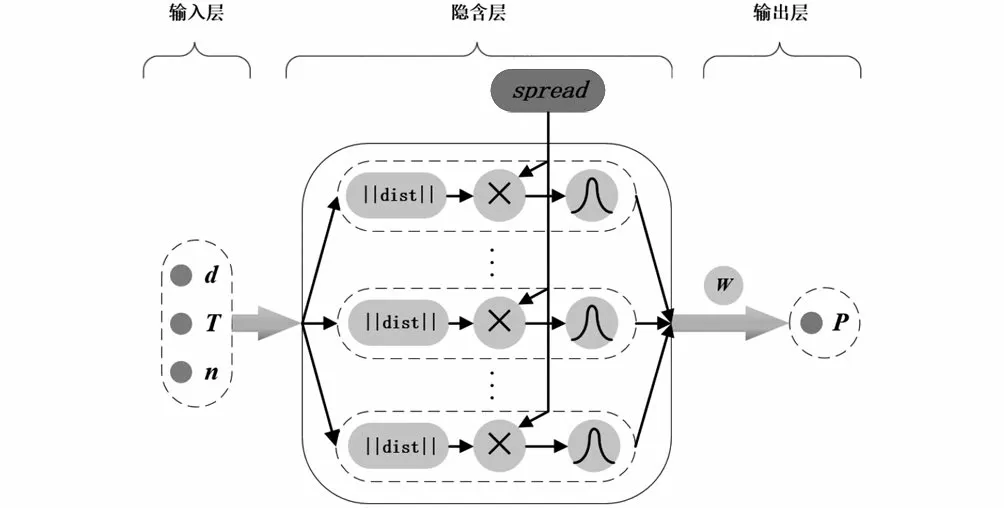
图4 RBF神经网络拓扑图Fig.4 RBF neural network topology

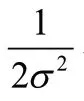
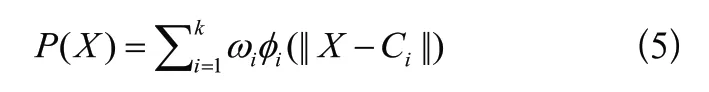
通过式(5)可知，RBF神经网络就是将每个数据从一个3 维非线性空间转换到一个维线性可分的空间，即对于组数据的输入X=(，，⋅⋅⋅，)与输出P=(，，⋅⋅⋅，P)存在式(6)所示关系。

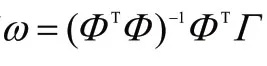
3.3 基于遗传算法的目标选择

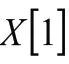
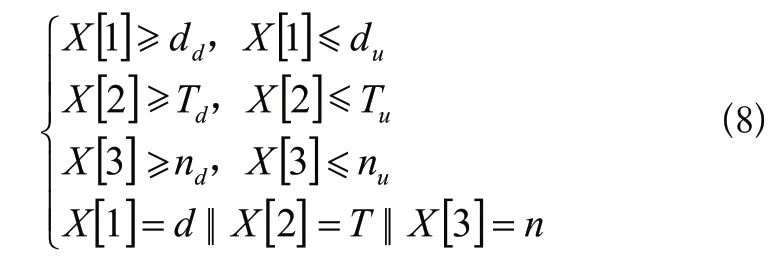
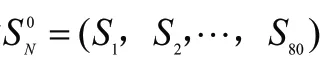
采用合适的选择算子与交叉算子，可以让遗传算法在解决高维非线性问题时，具有很好的鲁棒性，避免迭代过程发散；同时采用变异算子，可以使其通过种群间的变异来避免陷入局部最优解。确定遗传算法算子如下：选择算子采用轮盘选择；交叉算子采用点交叉；变异算子采用反转突变。在遗传算法迭代前，需要对初始种群进行编码以提高计算效率，本文采用格雷码编码，该编码方式对于选择交叉变异等算子具有更快速的计算能力，同时格雷码变化反映到实数上的变化为连续性，加快了迭代速度。

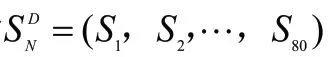
4 模型训练与试验验证(Model training and experimental verification)

4.1 模型训练

将500 组加工数据采取归一化处理，并分为400 组训练集与100 组测试集输入到RBF神经网络。设定网络参数如下：均方差目标为0.001，拓展系数为0.21。将训练集数据输入到网络模型进行训练，得到的迭代曲线如图5所示。

图5 网络学习迭代过程Fig.5 Iterative process of network learning

根据曲线变化，在第12 次迭代时，迭代误差为达到0.003，在第12 次迭代至第50 次迭代过程中，迭代误差变化相对较小。综上所述，第12 次迭代至第50 次迭代收益较小，在实际工程应用当中，对于误差要求较小的情况下，可选取12 次左右的迭代作为网络学习的结果。

将测试集数据与预测集数据进行对比，结果如图6所示，从预测值的结果来看，RBF神经网络模型的整体误差较小。在热封强度处于0到25时，预测集与测试集误差较大，但对于实际加工过程，为保证热封质量，不会选取该范围内的热封强度；在热封强度处于100到275时，预测集与测试集最大误差不超过5%，足以满足实际加工需求。为测试集与预测值进行直观的数据对比，采用式(9)计算其决定系数。

图6 预测结果对比Fig.6 Comparison of prediction results

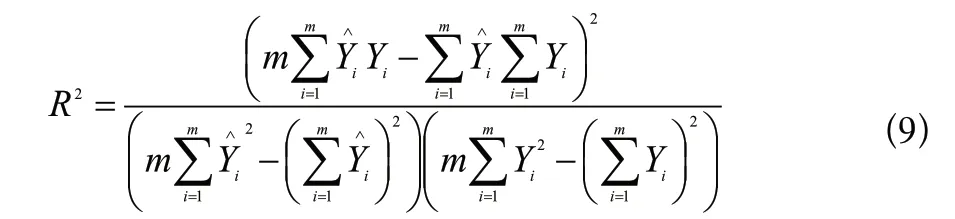
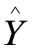
4.2 最优参数寻找

输入材料的屈服强度为267.65 N/15mm，根据式(3)取目标热封强度为160 N/15mm，设定三组实验：第一组实验设定热封距离为6 mm，第二组实验设定热封温度为180 ℃，第三组实验设定热封速度为80 包/min，同时迭代要求对于最优种群的热封强度均与目标热封强度误差小于5%，以种群平均适应度值为指标，迭代过程如图7所示，上述三组寻优迭代过程分别如图7(a)、图7(b)、图7(c)所示。

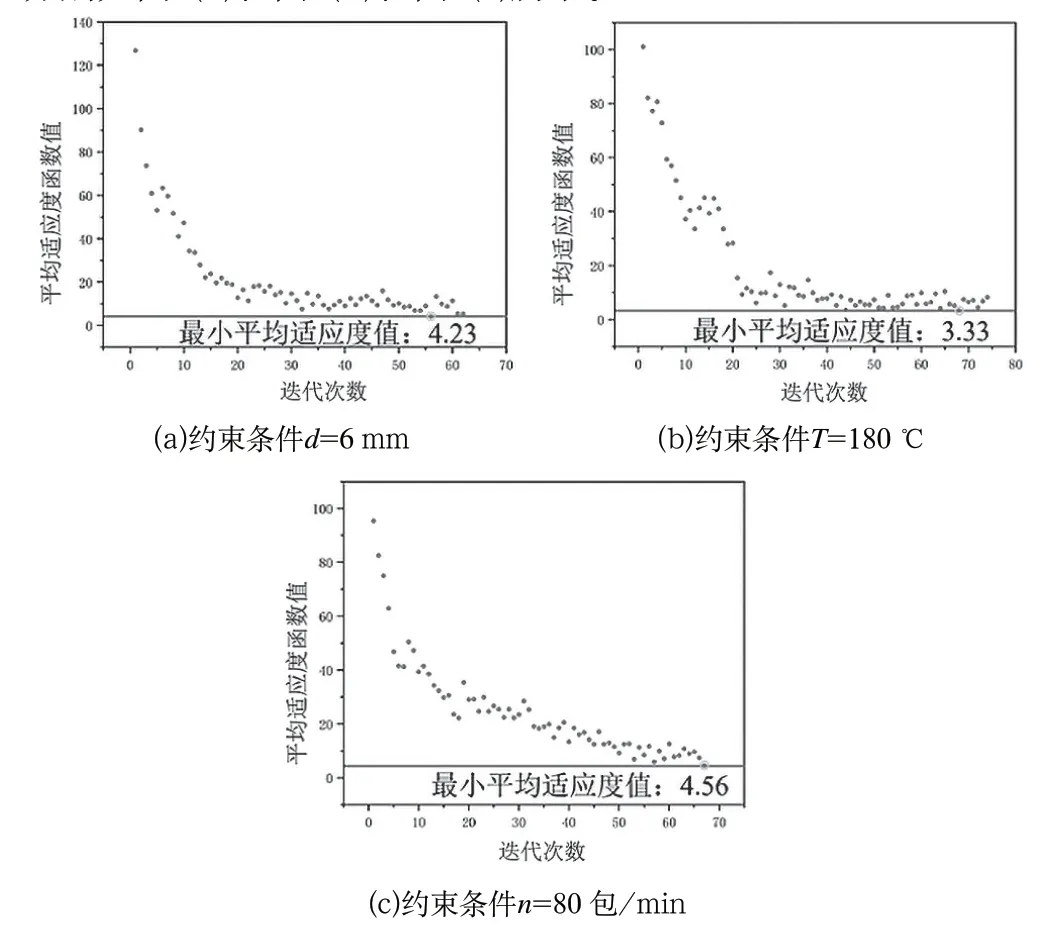
图7 参数寻优迭代过程Fig.7 Iterative process of parameter optimization

对于三种不同的热封强度，在迭代次数第10 次到第20 次时，平均适应度值快速下降，迭代次数20 次之后平均适应度值逐渐平稳，在迭代次数大概为70时结束，并且最终迭代结果收敛。对于不同的输入热封强度，都可以达到较好的结果，同时误差满足加工要求。

4.3 试验验证

每组随机选取最终寻优结果中误差最小的三组数据，得到如表1所示，在材料的屈服强度为267.65 N/15mm的情况下，3 组不同输入参数的决策最优解。

表1 最优参数寻优结果Tab.1 Optimization results of optimal parameters

将上述得到的最优工艺参数代入枕式包装机中生产加工，排除工况意外的产品，从各个情况中随机选取20 个加工产品进行热封强度测试，实验平台如图8所示。

图8 实验平台Fig.8 Experimental platform

将表1参数输入到枕式包装机中加工，再通过WDW-5型微机控制电子拉力试验机对加工产品进行热封强度测试，实验结果如图9所示，图9(a)、图9(b)、图9(c)分别为=[6,175,67]、=[7,180,73]和=[5,183,80]条件下，20 个产品热封强度分布图。

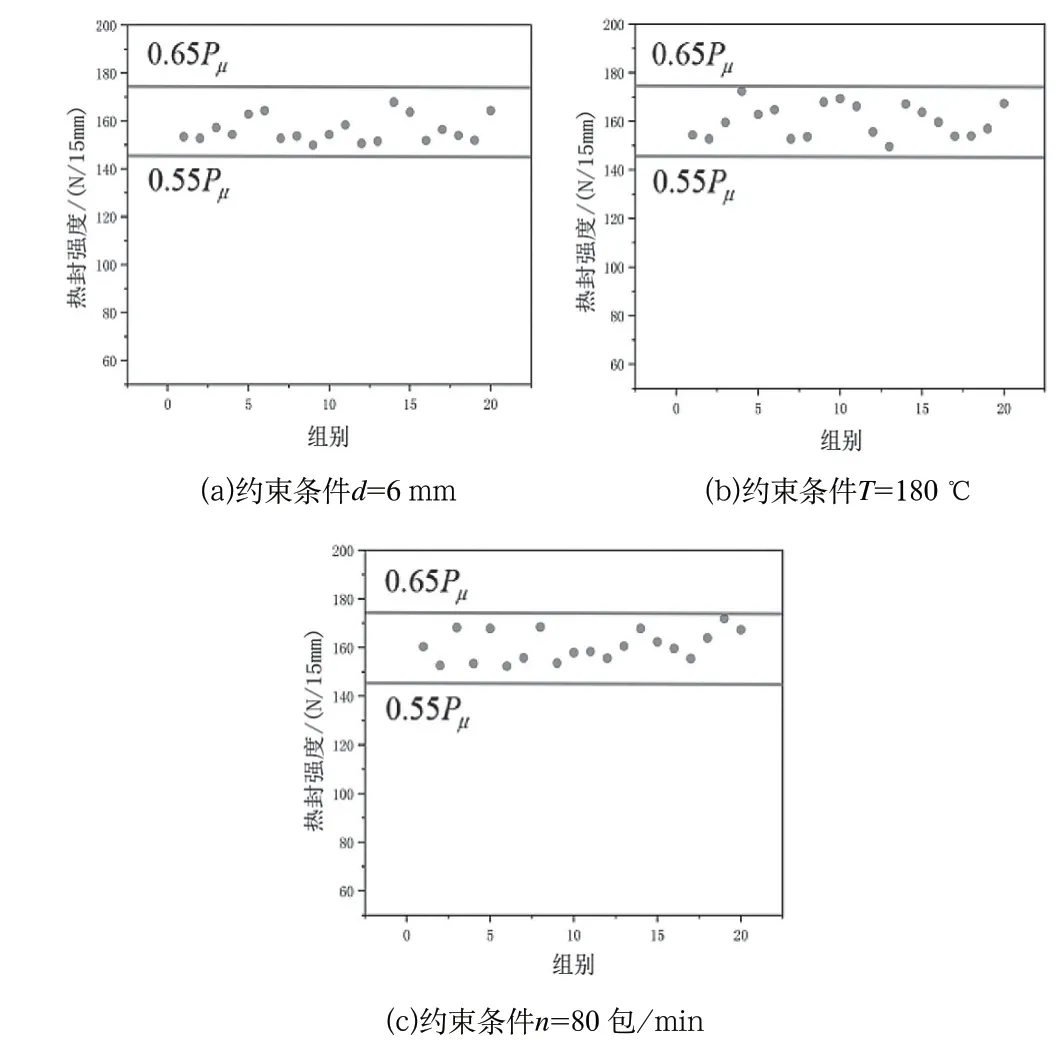
图9 产品加工验证结果图Fig.9 Result diagram of product processing verification

根据式(2)得出热封强度上下限范围，且图9中三组实验中抽取的每个加工产品都处于该范围，证明该方法得出的优化工艺参数在实际工程中有较高的合格率。

5 结论(Conclusion)

为实现对枕式包装机预先参数输入来提高加工效率，降低人力成本，构建了基于RBFNN-GA的工艺参数决策方法。

从实验数据中得出了不同工艺参数与热封强度的非线性关系，采取RBF神经网络对热封强度进行预测。通过数据集对比可知，基于RBF神经网络构建的回归模型具有较高的准确性与较快的收敛性，模型有效部分总体误差小于5%，因此该模型可以有效预测热封强度。

通过输入不同的参数，以RBF神经网络为基础设计适应度函数，再用遗传算法对最优工艺参数进行选择，最后得出最优的工艺参数。将最终结果带入到实际加工过程当中并且测定结果，20 组产品均处于加工要求范围内，满足加工需求。

本文提出的决策方法代替人工参数选择，有效地降低了人力成本，提高了决策效率；对于枕式包装机的智能化升级提供了理论依据。