中国老年寿命与健康寿命变动趋势研究

崔晓东，陈友华，周海花

(1 南京晓庄学院 商学院，江苏 南京 211171；2 南京大学 社会学院，江苏 南京 210008)

1 引言

健康寿命是指某确切年龄个体在健康状态下的期望生存年数。随着人口健康转型和老龄化进程地不断加深，“健康寿命比寿命更重要、提高健康期望寿命”(世界卫生组织，1997)已成为各国(地区)健康理念及人口健康监测指标。美国在1990年将健康寿命纳入健康政策优先指标，欧盟2010年明确提出到2020年健康期望寿命提高2岁，继而日本于2012年将健康寿命作为健康监测指标并提出至2020年健康寿命延长1岁以上。中国在2016年发布的《“健康中国2030”规划纲要》中首次将健康寿命纳入“国家战略”，并在“2030年具体实现目标”的第一条强调“2030年人均预期寿命达到79.0岁，人均健康预期寿命显著提高”的远景。然而，相关报告未明确中国目前的健康寿命是多少，也没有规划至2030年健康寿命提高多少的具体目标。其中一个重要原因在于国内关于健康寿命的基础性和前瞻性研究依然薄弱，测量方法和预测模型的理解和认识依然不甚清晰，尤其是中国健康本底数据缺乏(仅3-7期)导致基于大样本大跨度(通常20年及以上)的传统统计推断方法受阻，健康寿命规模和演变轨迹的精准把握难以开展，对其蕴藏的健康政策价值进行科学研判和深入挖掘亦存囿限。因此，本文尝试解决有限数据下健康寿命估计及预测过程中存在的统计推断问题，放松研究假设推导预测值及预测区间的明晰表达式，从而为中国老年健康变化趋势预测提供可选择方案。

2 文献回顾

健康寿命的概念自1964年提出以来相关研究逐渐丰富，概念界定和理论框架已渐成熟，研究内容不断拓展研究精度不断提升，其中更具可靠性和前瞻性的趋势预测和区间估计备受关注。综合国内外文献，健康寿命的预测主要包括统计推断和仿真模拟两种，仿真模拟包括宏观模拟和微观模拟，前者利用健康寿命和宏观环境的关系，通过对未来宏观情景(如经济、环境、社会、教育等关键因素)的模拟预测未来的健康寿命，目前不同国家已建立了各自的模拟模型，如美国的FEM(Future Elderly Model)、澳大利亚的NDIS(National Disability Insurance Scheme)、荷兰模型(Dutch Model)等，各国学者基于本国模型开展了健康寿命趋势预测(Ansah et al.,2015;Biddle & Crawford,2017)。与宏观仿真模拟不同，微观仿真基于微观个体特征(如人口统计学因素、健康行为等)模拟老化的过程，其优势在于能够包含更多影响健康的变量，尤其可以模拟不同健康政策的干预效果，该方法在美国、日本、英国、新西兰等地广泛使用(Wouterse et al.,2015;Gregg et al.,2018)，其中英格兰的PACSim(Population Ageing and Care Simulation)动态微观模拟应用比较广泛，尤其重要的是该模型的基线人群是35岁及以上，因而不需像大多数微观模拟一样需要做初始健康状况假设(Kingston et al.,2018a,2018b)。

仿真模拟的应用依赖于关键参数的设定，而关键参数设定具有鲜明的国家或地区特征，在缺乏高质量数据进行校准的情况下难以照搬或复制，在此情况下，传统的统计推断模型仍然是主要的预测方法，尤其适用于健康寿命研究不太成熟的国家或地区。传统推断方法沿用Sullivan(1971)技术估计健康概率，并假定未来健康模式保持不变或以某确定方式改变，例如计算目前的健康寿命/寿命比率并假设该比率在未来保持不变，然后根据未来的寿命值预测健康寿命，这种方法也被称为静态假设下的静态预测。部分学者从理论上证明了静态估计值的无偏和一致性特征(Madans,2011)，WHO公布的健康期望寿命、中国部分学者(李强等，2020)的研究均基于该方法，但随着社会经济、特别是医疗技术的发展，Sullivan方法的静态假设和健康模式时间同质性在健康期望寿命预测时遭到质疑，越来越多的研究发现健康模式并不总是保持一致，或者说并不在每一年龄上都保持一致(Bochen,2016;Jagger,2016)。

鉴于未来健康模式的不稳定，而传统外推程序没有考虑健康变化的随机性，缺少适当的统计结构和模型，也很难将这些估计值解释为点估计，尤其缺乏健康寿命方差的估计方法，妨碍了置信区间的估计及估计的显著性检验，因此建立包含时间相关项、能够反映健康模式变化特征的动态预测随机模型成为趋势。其中，Lee和Carter(1992)建立的随机死亡率动态模型(Lee-Carter)将丰富而简洁的人口统计学模型与时间序列方法相结合，因模型不依赖于宏观情景假设并能提供估计值的预测区间而具有强大优势(Chavhan,2016)。然而Lee-Carter模型本质上是时间序列模型，强调对大样本长时序历史数据的追溯，有限数据下模型拓展研究已有部分文献开始涉及(Nan,2004;杨贵军、刘帅，2015)，但大多属于对参数估计方法的改进，缺乏系统地理论推导及现实应用，且未能给出预测期间的明晰表达式。基于此，本文基于Lee-Carter模型并尝试对其进行拓展，以健康变化差分项独立同分布为切入点推演有限时序数据下的健康寿命区间预测表达式，结合中国老年健康追踪调查数据，按性别年龄别估计并预测中国老年寿命和健康寿命，以期为相关老龄政策的制定提供数据支持，为寿命与健康寿命演变关系提供可参考答案。

本文的边际贡献：在缺乏高质量数据对仿真模拟进行校准情况下，试图利用传统推断统计方法建立预测模型；考虑到外推模型无法反映健康变化的时间特征，在Lee-Carter模型基础上建立包含时间相关项的动态预测模型；针对时序数据有限无法满足传统假设，尝试以健康变化差分项为切入点，推导预测值及预测区间的明晰表达式。结合所建模型及中国老年健康数据，预测老年健康寿命的变化轨迹并对老年健康变化模式进行实证检验。

3 研究方法

3．1 Lee-Carter基础模型

Lee-Carter模型起源于死亡率的动态预测，其原理和方法目前已被广泛应用于死亡率和寿命的预测(Ermannoet et al.,2009)。尽管健康概率和死亡率不存在必然联系，两者的影响因子也不相同(Manton,1982)，然而大部分文献认同死亡作为健康状态的一种，用于预测寿命的模型形式大都适用于健康寿命的预测(Jagger et al.,2020；Maria et al.,2017;Brian et al.,2016;黄枫、吴纯杰，2012),尤其是基于时间序列数据的预测(Bochen,2016)。本文利用Lee-Carter模型预测寿命和健康寿命，并以寿命预测为例进行公式推导，借鉴Lee-Carter模型，寿命预测包括如下两个步骤。

一是利用已有调查数据将特定年龄预期寿命的对数描述为独立于时间的年龄成分与年龄成分随时间变化的时变因素之和，如式(1)：

ln(LEx(t))=αx+βxkt+εx,t

(1)

其中，ln(LEx(t))表示x岁群体在时期t的预期寿命对数，x=(x1,x2,L,xm)t=0,1,L,T，xm为最高年龄或最高年龄组，T为调查次数，也代表最后一次调查的时期。αx为不同时期x岁预期寿命对数的均值，可表示寿命的年龄模式，kt为预期寿命随时间变化的时变因子，βx表示x岁群体对时期变化的敏感度，βxkt是由年龄和时期构成的m×T矩阵且对应列成比例，可以用矩阵Z表示，εx,t为随机误差项。

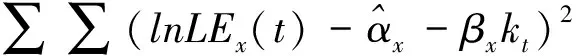
(2)

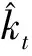
(3)

为提高预测精度，通常以最后观察期T的寿命值为基准进行外推(Ermanno & Michel,2009)，即：

(4)

本文也将根据式(4)进行预测。

3.2 有限数据下的Lee-Carter模型

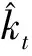
kt=kt-1+d+ξt

(5)

其中d为漂移项，ξt为随机误差项，且ξt～N(0,σ)。

需要注意的是，式(5)的建立通常需要大跨度的连贯数据，针对数据有限的情况，本文尝试以时变因子差分项[kt-kt-1]为切入点展开讨论。

假设对于不同的t，[kt-kt-1]是均值d标准差为σ的独立同分布变量，两参数估计值可表示为式(6)：

(6)

(7)

(8)

(9)

(10)

进一步地，将式(9)代入式(4)，即可得到LE(x,t)的点估计如式(11)：

(11)

kt为正态分布，那么LEx(t)服从对数正态分布，结合式(10)，LEx(t)的期望值和方差为式(12)和(13)：

(12)

(13)

根据式(12)和(13)，即可得到各年龄预期寿命的区间估计。

最后需要说明的，以上公式适用于相同间隔的调查期，如果间隔期不同，如三次调查分别在2000，2003，2008年，前两次间隔3年，后两次间隔5年，那么[kt-kt-1]不再满足独立同分布假设，d的估计值虽仍可按上述方法获得，但σ的估计相当复杂。当然也可以对基础数据进行处理，将不同间隔转化为相同间隔，这将是后续研究的一个重点。本文所用数据调查间隔相同(其实大部分调查研究的间隔期都相同)，因此本文的计算将基于以上公式进行。

4 研究结果

4.1 数据来源及概念界定

本文数据来源于北京大学健康老龄与发展研究中心组织的中国老年健康影响因素调查(CLHLS)项目，CLHLS遵循严格随机抽样原则，调查范围包括全国23个省市中的800多个县市区，基于对主要健康指标的可信度和效度、代答或不应答比率、样本信息缺失程度、内部逻辑错误的比率和死亡率可信度的全面评估及众多学者的使用分析，CLHLS的数据质量被证明是令人比较满意的(曾毅，2017)。CLHLS为始于1998年的三年期纵贯调查项目，目前已开展七次，因前两次调查对象主要是80岁及以上高龄老人，本文以2005-2008、2008-2011、2011-2014及2014-2017四次调查数据中65岁及以上老人为研究对象，其中2014-2017年的计算结果既用于稳健性检验，也是预测的起始年份。删除重要信息缺失和失去追踪样本，其中重要信息包括分组信息(如年龄、性别、居住地)和健康分类信息(下文所提到的ADLs项目)，最终样本信息如表1所示。

表1 样本信息及状态界定

本文健康概念的界定按照惯例采用日常生活自理能力(ADLs)作为评价标准，ADLs包括六项指标(洗澡，穿衣、室内活动、如厕、进食和控制)，根据ADLs完成情况，将全部六项活动均能独立完成视为健康(状态1)，有一项或大于一项不能独立完成作为不健康(状态2)，包括死亡(状态3)共三种状态，其中状态1和2为可转移状态，即健康可转为不健康，不健康也可恢复健康，状态3为吸收状态。CLHLS项目采用问答形式(对应编号e1-e6)，相关行为能够无辅助完成得分1，其他情况为0，如表1第(3)列。

作为入驻育成中心的一家IT企业，宁夏希望信息产业公司2013年组建团队，瞄准住房公积金软件和平台开发，建立起从软件开发到平台运营的完整的产业链。其开发建设的宁夏公积金大数据平台集中管理公积金数据，被住建部认定为公积金大数据平台建设的标杆项目。如今，公积金大数据平台项目已在新疆、辽宁落地，2017年5月又成功中标江苏盐城住房公积金项目。

4.2 寿命与健康寿命估计

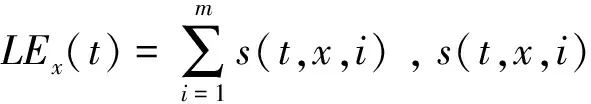
图1 健康状态转移路径示意图

在计算之前首先将样本按年龄和性别分组，本文选择3个年龄为一组比通常5年一组更详细，同时又因为调查间隔期为三年，兼顾了计算的便利性。同一年龄组内再按健康评价标准分为不同状态组，追踪每小组观察期末健康状态的变化，根据人数的变化计算生存概率s(t,x,i)或健康概率p(t,x,i)。需要说明的是，由于死亡是不可逆的，生存概率s(t,x,i)的计算根据各组生存的人数即可得到，但健康概率p(t,x,i)的计算涉及多种路径，比如计算p(t,x,2)，可能存在如图1中健康-健康-健康和健康-不健康-健康两条路径，期限越长或者状态越多涉及的转移路径也越多。

表2 时期-性别-年龄别寿命及健康寿命

如果调查间隔如一年或半年时间比较短，可以假设状态间不发生转移并根据起始状态和到达不同状态的人数比例计算转移概率，但大部分项目并不是每年都进行，本文使用的CLHLS数据为三年度纵贯调查，上述假设可能会带来较大误差，因此本文借鉴Michel和Wagner(2020)和Zeng(2017)的研究方法，采用马尔可夫(Markov)方法计算转移概率，由于篇幅所限且该部分不是本文研究重点，略去备索。基于Markov方法计算分时期的性别年龄别寿命和健康寿命如表2。

根据表2可以看出，以2014-2017年为例，65-67岁女性老人剩余寿命和健康剩余寿命分别为15.89和13.24年，不健康寿命为两者之差，即2.65年。男性老人对应数据分别为14.11、12.24和1.87年。该结果与乔晓春和胡英(2017)的计算结果(男性健康余寿12.62，女性13.73)、杜鹏和李强(2006)的结果(男性健康余寿12.05、女性13.65)及黄匡时(2018)预测的60岁及以上健康寿命为15.8比较接近。另外性别对比看，女性老人寿命和健康寿命均高于男性，同时女性的不健康寿命也明显高于男性，女性长寿未必健康的结论与大多数文献一致。

4.3 寿命与健康寿命的预测

该部分包括三个步骤：首先根据已计算的前三次寿命和健康寿命值(见表2中2005-2008、2008-2011和2011-2014)，计算Lee-Carter模型参数αx、βx和kt；然后利用模型预测2014-2017年寿命和健康寿命，并将其与实际估计值(表2中2014-2017列)进行比较，以检验模型稳健性；最后以2014-2017年的实际估计值为基准，预测2026-2029年分年龄别性别的寿命和健康寿命及置信区间。

4.3.1 参数估计

图2 不同参数的估计值注：为简化表述，图中各观察期用中间年份代替，如2008-2011用2010代替，其他同。

4.3.2 稳健性估计

本文将基于截面数据计算的2014-2017分年龄和性别寿命及健康寿命与采用本文预测方法的预测值相比较，根据两者偏差考察模型稳健性，计算结果如表3。

表(3)中预测值是利用前三次的计算结果和本文方法预测的2014-2017年寿命和健康寿命，绝对偏差是观测值(见表2相应列)与预测值(表3相应列)之差，相对偏差是绝对偏差与观测值之比。从相对偏差来看，基本低于通常要求的10%以内的标准，尤其低龄老人预测精度较高，可作为数据有限情况下寿命和健康寿命预测的备选方案，但也需注意偏差较大的个别年龄，如92+岁女性寿命的相对偏差达9%，那么在引用时可能需要校准。

4.3.3 寿命及健康寿命的预测

以2014-2017年估计值为基础，本文以三年度为单位预测了未来四期的分年龄性别寿命、健康寿命及置信度为95%的置信区间，篇幅所限，本文给出2026-2029年的预测结果如表4，图3直观显示寿命和健康寿命的性别差异。

表3 稳健性检验

表4 2026-2029年寿命和健康寿命预测值

图3 2026-2029年寿命及健康寿命预测值及预测区间

表4数据显示，预计2026-2029年间65-67年龄段的女性和男性老人剩余寿命分别为18.07和15.81，健康寿命分别为14.55和13.01，对应的不健康寿命为3.52和2.80。本文试图对预测结果进行比照研究，发现可直接对比的方案比较欠缺，但可以将“健康中国 2030”规划纲要中“2030 年人均预期寿命达到 79 岁”的远景目标及2015年联合国世界人口展望预测的79.08岁(男性77.75，女性80.46岁)作为参考。对比来看，本文2029年的预测值均大于对照组2030年的预测值，考虑目前预期寿命没有下降的趋势，所以认为本文的预测值相对较大。其原因可做两方面的解释，一是规划纲要中的79岁是指出生时预期寿命，即0岁时剩余寿命，而本文计算的65-67岁的预期寿命是指已经存活至65-67岁的剩余寿命，显然在此之前的生存率为1，因此计算结果会大于出生时寿命。同理也可以看到现阶段68-70岁的女性老人剩余寿命为16.16，两者相加寿命为85.16，也大于现阶段65-67岁老人84.07的预期寿命；另一个可做样本选择性偏差的解释，本文删除了重要信息缺失及不能加以追踪的样本，剩余的参与调查的样本通常具有较好的健康状况，从而导致结果偏高。庆幸的是本文给出的是一置信区间，结果具有一定科学性和弹性。健康寿命的预测现有研究不多，其中李成福等(2018)基于经合组织国家数据、与中国预期寿命近似国家数据和与中国健康预期寿命近似国家的数据并利用年均增加值方法，预测2030年时0岁健康预期寿命平均值女性73.17、男性69.12岁，本文预测值同样大于该文献结果，其原因可做类似解释。

5 寿命与健康寿命的进一步探讨

5.1 健康变化模式验证

增龄是包括中国在内的各个国家和地区人口变化的共同特征，然而所增长的寿命是健康还是不健康寿命是比单纯长寿更值得关注的议题，因为不健康寿命的长短将直接关系到社会医疗卫生服务需求投入和疾病经济负担的多寡。事实上，许多国家在进入老龄化社会后普遍出现了健康和长寿不同步、甚至是不一致的情况。Manton早在1982年就指出死亡率和发病率不存在必然联系，并提出根据死亡率、发病率及疾病程度判断健康变化模式的基本标准。后来在此基础上依据疾病程度发展出不同定义(Jagger et al.,2020;Maria et al.,2017;Brian et al.,2016)，本文对疾病程度不加分类，采用最简单也最本质的分类方式，即发病率压缩、发病率扩张和动态平衡模式，分别对应于健康寿命与寿命的占比(HLE/LE)变大、变小和基本不变三种模式。本文对比中国2014-2017和2026-2029两时期老人寿命和健康寿命，并根据HLE/LE变化情况对健康变化模式加以验证(如图4)。

图4 老人健康变化情况

图4主坐标轴显示的是与2014-2017年相比2026-2029年分年龄性别寿命和健康寿命变化情况，寿命和健康寿命间的差异即为不健康寿命，由图可以看出无论男性还是女性，寿命、健康寿命和不健康寿命在各年龄段都有不同程度增加，相对而言女性寿命增长幅度更大，尤其低龄老年女性寿命增长非常明显。就健康寿命而言，男性和女性的差异并不显著，占优的寿命与无差别的健康寿命使女性不健康寿命比男性更长，也意味着未来女性的照料问题将更加严峻。

图4次坐标轴显示老年健康变化模式。健康模式既指健康余寿在余寿中的占比随年龄的变化，即同一观察期不同年龄上HLE/LE的变化，也指与历史时期相比，所增加的寿命中更多的是健康寿命还是不健康寿命，表现为两个时期同一年龄上HLE/LE的对比。根据图4，首先比较年龄模式，总体来看两个时期HLE/LE均随年龄呈下降趋势，即年龄越大剩余寿命中不健康时间占比越多，大部分年龄的健康寿命占比均明显大于50%，尤其低龄老人。男性HLE/LE比值在83岁左右出现了回升，可能的原因是男性在74岁左右遭遇高死亡率(如图中显示74岁男性寿命增量明显下降)，经过死亡选择的老人通常有更好的健康状况。时间模式来看，对比同一年龄上两个时期的HLE/LE值，发现并不存在明显变化，也就是说寿命和健康寿命的变化速度基本同步，不存在明显的压缩或扩张，处于动态平衡模式。这一结果为用比例法计算未来医疗费用支出等的预测提供理论支持。

5.2 老年健康变化的国际比较

延长健康寿命是世界各国关注的问题，联合国在千年发展目标(2000～2015)结束之际又制定了2030可持续发展目标(SDGs)，在《可持续发展指标框架体系》中明确提出将健康寿命纳入可持续发展的主要健康监测指标，各国卫生部门也都相应建立健康预期寿命的监测数据库。为了对中国老年健康发展状况有直观了解，本文进行了健康预期寿命的国际比较，主要根据全球健康研究组织(IHME)在Lancet(柳叶刀)上发布的数据，梳理了近年来将健康预期寿命纳入国家规划的国家和国际组织的健康预期寿命发展状况。参照李成福等(2018)的分类，分别以经合组织国家、与2013年与中国平均寿命接近的部分国家和地区及与2005年与中国平均健康寿命近似的国家和地区作为比较对象。由于所得数据跨度不同，本文通过计算年均增加量进行比较(如表5)。

表5 不同国家和地区健康寿命年均增量

需要说明的是，表5中其他国家或地区年均增加是0岁健康寿命，严格说来与本文65-67岁健康寿命不具可比性，但我们仍可得出一些信息：一是65-67岁健康寿命与出生儿健康寿命增长速度的差异来看，前者远低于后者，间接说明健康寿命的改善更多来自于包括新生儿死亡率和成人死亡率的降低，同时由于新生儿的死亡率已经很低及成人死亡率相对稳定，使得平均健康寿命增加的速度减慢，表5中大部分国家2005-2013年间的0岁健康寿命增长率大于1990-2005年间的增长率印证了这一结论；二是与其他国家年均增长速度出现不同程度下降相比，中国在2017-2029年间老年健康寿命年均增长速度不低于2005-2017年，尤其男性老人的健康寿命，说明我国在这一时期仍处于健康红利期，这对于又多又老的中国人口国情无疑是利好消息。

6 结论与讨论

自1997年《世界卫生报告》呼吁关心预期寿命的同时更要重视健康预期寿命以来，健康预期寿命在相关国际研究、国际政策的战略规划中逐步被推广应用，目前已被大多数国家和地区纳入可持续发展的主要健康监测指标并制定了明确的健康寿命发展规划，中国政府也在《“健康中国2030”规划纲要》中明确提出2030年显著提高健康预期寿命的远景目标，但或许因为中国健康本底数据相对缺乏相关研究还不丰富，规划纲要并未提供具体的规划数据，本文尝试建立有限数据下寿命和健康寿命的估计及预测模型，结合中国老年健康数据对中国老年的健康及变化趋势进行预测。

既往数据有限情况下的寿命预测通常采用增量法、比例法等传统外推方法，传统外推方法使用简单但未能考虑健康变化的随机性且缺少适当的统计结构和模型，构建包含时间相关项的动态预测模型、且考虑健康变化随机性的区间估计将使结果更具严谨性和科学性。本文正是基于这一目的，在Lee-Carter模型基础上推演有限时序数据下寿命及健康寿命的预测值及置信区间，并结合研究结果回应了中国老年健康变化模式及国际比较。本文模型能够为同类问题的研究提供可对比方案，同时模型具有较大扩展和适用性，比如用来预测未来失能人口规模、失能时间及长期照护费用；或考察不同教育程度、收入水平或社会地位老年健康的异质性，尤其适用于个体信息不很丰富且追踪调查跨度不大的情况。

本文为有限数据下研究老年健康动态变化提供新思路，同时，本文的研究结果可以为中国老龄社会背景下公共政策评估和讨论提供参考。首先，本文结果显示老人余寿中健康寿命仍占较大比例，尤其低龄老人余寿中约有80%左右处于健康状态，且男性和女性比例相似，该结果一方面为中国政府逐步延长退休年龄政策提供客观基础，另一方面也说明低龄老人具有参与劳动市场的潜力，延长退休并为健康活跃的老人提供工作机会具有可行性和必要性。其次，老人健康模式的年龄特征来看，年龄越大健康寿命占比越小，因此政府公共健康政策的制定既要考察生命长度更要关注生命质量这一根本问题，在大力发展老龄健康服务项目的同时，着力于研究提高寿命延长后有效改善健康水平的科学途径，努力实施高效的个体化健康干预方案，逐步实现健康且长寿的健康老龄中国梦。最后，未来中国老年寿命、健康寿命及不健康寿命均将继续增长，健康寿命的改善速度基本能够匹配寿命增长速度，老年健康基本处于动态均衡模式，但仍需注意该结果与“健康中国”长寿且健康目标的差距，可以尝试将健康寿命纳入中央和地方各级政府优先考核指标，不仅有助于从指标层面促进健康管理，而且可以衡量一个地方居民的健康水平以及评估政府的健康政策和健康干预效果。同时考虑到健康寿命的改善更多依赖于早期和中期生活方式，老年期的改善空间相对有限，也就是说健康寿命其实是一个全生命周期的概念，关口提前加强预防管理可能起到事半功倍的效果。

最后，尽管本文丰富和补充了与健康寿命相关的研究文献，仍存在一些值得探讨的问题，一是健康概念本身。和大多数文献相似，本文的健康界定仍局限在生理健康领域，但实际上健康不仅仅指没有疾病或身体不虚弱，还包括精神上和社会适应性等方面处于完整的良好状态、是一个多维的动态概念，尤其老年健康的测量更应该考虑老人心理、精神、情绪等诸因素，那么未来结合社会技术发展重新思考并界定老年健康开展分析成为必要。二是样本选择性偏差，如前文所述，因健康状况糟糕的个体更可能失去追踪或不易被调查，可能导致估计值偏高，尤其是高龄老人余寿的估计。所幸本文样本的代表性及样本量规模在同类问题的研究中优势仍非常明显。三是研究内容上，全生命周期(儿童期，成年期和老年期等)健康变化的比较研究以及健康影响因素的追溯研究，可能为“健康中国”的实现提供更具针对性和更具体的策略。