对三十多年来中国出生人口的估计

乔晓春

(北京大学 人口研究所，北京 100871)

1 背景和目的

每年年初国家统计局都会在《国民经济和社会发展统计公报》上发布上一年年末全国总人口、上一年全年出生人口、死亡人口、出生率、死亡率和自然增长率。除了人口普查年份外，公布的历年数据均是通过当年全国人口抽样调查结果推算得出。

一些基层计划生育工作者在上个世纪80年代和90年代都发现出生人口存在严重漏报(傅世珍，1989；孙学礼等，1993)。1990年人口普查结束后国家统计局发现1982年以来根据历次人口变动抽样调查得出的出生人口存在很大程度的漏报，从而基于普查数据对1983年到1989年期间历年曾经公布过的出生率进行了重新调整，比如将1983年出生率从18.22‰调整到20.19‰，1986年从20.77‰提高到22.43‰，1989年的从20.83‰调整到21.58‰(1)1990年人口普查之前公布的出生率参见国家统计局人口统计司编：《中国人口统计年鉴(1990)》，北京：科学技术文献出版社，1991年，第612-613页；调整后的出生率参见国家统计局人口统计司编：《中国人口统计年鉴(1991)》，北京：中国统计出版社，1992年，第369页。。

正是由于1990年人口普查发现1980年代调查出生人口漏报率非常严重，1990年以后国家统计局接受了之前的教训，不再等到下次普查结束后再重新修订之前公布的数据，而是在当年数据公布之前就先行进行调整。比如，1993年和1994年人口变动抽样调查结束后，根据事后质量抽查发现1993年和1994年出生漏报率分别为6.9%和6.4%，分别影响出生率1.12和0.98个千分点。然而，由于“感到”出生人口调查难度逐年加大，瞒报和漏报越来越严重，统计局在考虑事后质量抽查估计误差基础上，进一步选取调查误差和抽样误差的上限进行修正，“尽了最大(努力提升)上调幅度”，将1993和1994年出生率在直接调查结果的基础上分别上调了2.51和2.38个千分点(贾同金等，1995)，从而将1993和1994年出生率从调查得到的15.58‰和15.32‰，直接提升到了公布时的18.09‰和17.70‰(见表1)。根据1995年1%人口抽样调查直接计算得到的1994年10月1日至1995年9月30日出生率为13.53‰，总和生育率为1.46(2)这两个数据是通过《中国人口统计年鉴1996》第二部分“1995年全国1%人口抽样调查数据”中第108页表2-18和第76页表2-6的(样本)总人口计算得到的。。这些结果无论与统计局1993年和1994年公布的出生率比，还是与1990年人口普查得出的2.31的总和生育率比，都显得过低了。最终，统计局将1995年的出生率调整为17.12‰，提升了3.6个千分点，但并未对外给出总和生育率的估计。按照这样的上调幅度，整个90年代平均每年补进了200多万的出生人口，估计十年中累计补了2000多万出生人口。

在2000年第五次人口普查开始之前，尽管政府各部门都期望能把出生人口和生育率搞准，但各部门都有自己的担心。统计部门担心真实调查结果得不出人为上调进去的2000多万出生人口；计划生育部门则害怕突然多出2000多万出生孩子(乔晓春，1999)，因为在计划生育的统计数据中并不存在多生的这2000多万人(3)因为如果真的在人口普查时多出2000多万的出生人口，则意味着计划生育部门工作的失职或失败。为了在2000年普查开始之前摸清出生人口底数，国家计生委于1998年在全国范围内开展了出生人口的“清理清查”工作，但并未发现存在大量漏报的出生人口。。普查结果出来后，这2000多万补进去的出生人口人并没有出现。然而，由于以往历年人口数据已经公布，不允许将已经公布的总人口重新降下来，最终将多出的这部分人以普查登记漏报的名义补充到了公布的全国总人口中(乔晓春，2002)。最终国家统计局也承认，2000年人口普查全国共计漏掉了2322万人(4)在国家统计局于2002年8月份出版的《中国2000年人口普查资料》(中国统计出版社)编辑说明中明确指出：“本资料总人口(即通过个案数据汇总后得到的人口)为124261万人，比国家统计局根据快速汇总(或2000年第五次全国人口普查主要数据公报)发布的总人口126583万人少2322万人”。。此时，官方并未承认“这2000多万出生人口实际上并不存在”，而是认为这2000多万人被人口普查漏掉了。

2000年第五次全国人口普查短表中得到的出生人口为1411.5万人，总人口为124261.2万，出生率为11.39‰；从长表中得到的样本出生人口为118.2万，样本总人口为11806.7万人，直接计算的出生率为10.03‰，样本计算结果比总体计算结果低了1.4个千分点。即使使用总体计算结果，出生率仍然很低，因为普查之前已经公布的1999年出生率为14.64‰，出生人数为1834万。而用样本数据直接计算得出的总和生育率更是远远低于人们的预期，只有1.22。国家统计局有关人员认为“总和生育率低于计划生育政策水平，……，似乎难以解释”，并认为“普查实际登记的0-9岁人口存在一定程度的漏报”(张为民等，2003)。

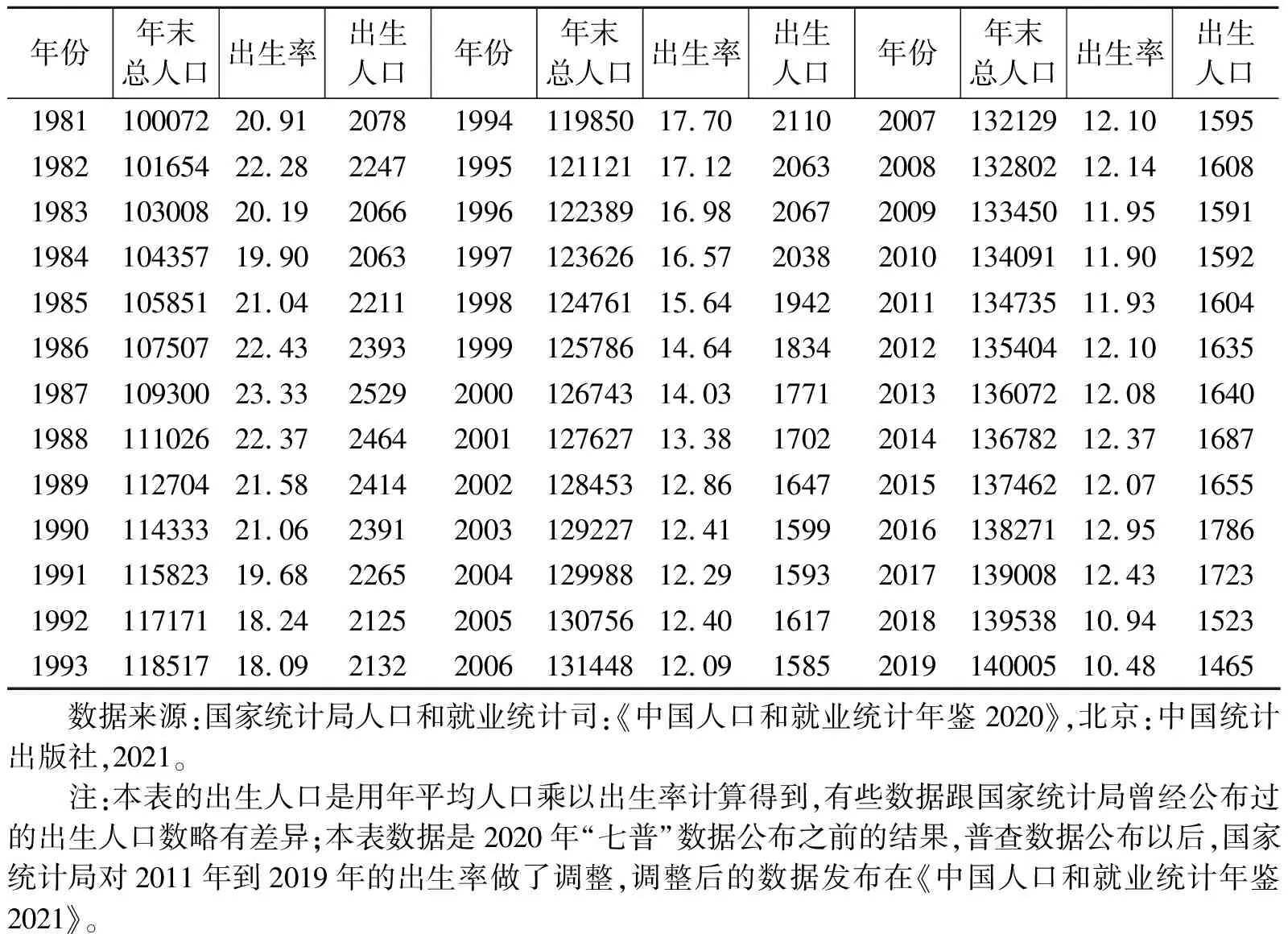
表1 官方公布的1984到2020年年末全国总人口、出生率和出生人口(万人，‰)

上世纪80和90年代形成的“调查出生人口严重漏报”的观念在2000年人口普查继续被强化了，并在官方和学者的头脑中固化了。从2000年以后统计局仍然不公布每年人口抽样调查直接得出的出生率，而是跟普查之前一样，经过上调后才公布。比如，官方公布的2001年和2002年出生率分别为13.38‰和12.86‰，均比直接计算得出的结果高出了2个千分点左右(5)根据2002和2003年发布的《中国人口统计年鉴》中2001年和2002年全国人口抽样调查数据，2001年直接调查得到的样本出生人口为13853人，全部样本人口为1220559人；2002年调查到的样本出生人口为13668人，样本总人口为1258951人。用样本出生人口除以样本总人口二者分别为11.35‰和10.86‰。《年鉴》的编辑说明中提到，公布的出生率是“经加权后汇总”得出的结果。尽管加权后的结果会与直接计算的结果有所不同，但差异不会这样大，而且不会全部偏向同一个方向，且偏离的程度基本一致。。这里存在的一个问题是，尽管认为出生存在漏报，但是漏报率并不是一成不变的，官方在调查数据基础上上调出生人口或出生率时肯定会对漏报率给出判断，但这种判断是否准确是不得而知的。

表1给出的是2020年国家统计局公布的数据，从中可以看出，出生率从1987年达到最高值后逐年开始下降，在个别年份存在小的波动，到2010年达到最低值。这意味着官方认为在计划生育的作用下中国人口出生率一直是持续下降的。2010年以后出生率和出生人数开始出现小幅上升，只是在2013年底出台的“单独二孩”政策和2015年底出台的“全面二孩”政策后的2014年和2016年出生率和出生人口均有一定的提升，随后的一年又开始下降。

2020年第七次全国人口普查结束以后，国家统计局对2011年到2019年这十年公布的出生率再次进行了调整，并对初期的结果进行了大幅度的上调，同时也对政策调整后1-2年的出生人口进行了大幅度的上调(乔晓春，2021)，国家统计局于2021年在《2021中国统计摘要》中公布了调整后的结果(中国统计出版社，2021)。

“七普”数据发布后，官方公开承认人口普查得出的1.3的总和生育率是准确的，登记的1200万出生人口是准确的，这是三十年来官方第一次承认普查登记的出生人口和总和生育率是正确的。官方也公布了普查漏报率，只有0.05%(6)本次普查漏报率低主要有以下几个原因：一是将现有人口和户籍人口同时登记，从而让人户分离人口在现住地和户籍地都进行登记，大大避免了人户分离人口的漏登；二是以往普查人们由于担心计划生育超生处罚，出生人口和婴幼儿漏报非常严重，而本次普查是在已经全面放开二孩政策或计划生育处罚几乎已经消失的情况下进行的，从而导致出生漏报会大大降低；三是本次普查第一次登记了身份证号，从而可以将普查登记人口与公安身份证登记系统数据进行比对，大大避免了人头的丢失；四是第一次使用大数据手段将普查登记数据与政府相关数据和互联网数据进行比对。尽管以上四个原因会在很大程度上保证本次普查数据相对以往普查更为准确，但并不能保证数据绝对准确。这里讲的只是“相对准确”。，这意味着普查整体上数据质量较高，这为我们估计以往的出生人口提供了好的基础和条件。本文的目的就是利用本次人口普查数据，结合2000年和2010年第五和第六次全国人口普查数据，对以往三十多年来中国历年的出生人口(7)本文没有估计(粗)出生率，原因是出生率不仅由出生人口决定，还与总人口规模有关。对出生人口的重新估计隐含着总人口也会随之变化。因为本文不涉及对总人口数的估计，所以也不会涉及对出生率的估计。进行重新估计。

2 数据和思路

2.1 使用的数据

本文将主要使用2000、2010和2020年三次全国人口普查包括现役军人的分性别和年龄人口数据；为了计算队列存活率，本研究还使用了这三次人口普查分性别和年龄死亡率，用来估计队列存活率；为了将跨年出生队列转为日历年内出生队列，还利用了三次人口普查出生人口在出生月份上的分布数据。

三次普查的漏登率分别为1.81%，0.12%和0.05%。单纯从漏登率上可以大体判断，2020年第七次人口普查准确性最高，其次是2010年第六次人口普查，2000年第五次人口普查登记质量会相对差一些(8)因为2000年人口普查给出的漏登率并不是事后质量抽查得出的漏登率，而是基于以往各年公布的人口总数推算出的人口普查总人口和普查实际登记总人口的差异计算出来的，所以这一结果并不能真实反映普查的登记质量。。这样，本文对三次普查分性别和年龄人口数据准确性的判断，与普查整体质量高低的判断基本一致。

2.2 估计的思路

本文对出生人口数的估计是分性别和分队列进行的。估计的思路很简单，即使用逆存活率方法回推各队列人口出生人数，再将队列出生人口转换为年度出生人口。这里假定中国人口是封闭的，至少2020年时0-34岁男性和女性各年龄人口在之前的年份不存在万人以上的国际净迁移(9)因为本文使用的不同性别、不同年龄人口以万人为单位，而不是以个人为单位，所以万位以下的数据波动对估计结果没有影响。。

如果t表示观测时间(一般为三次普查的标准时点)，x表示年龄，B(t-x)表示t年x岁队列人口在t-x时间出生时的人口数，Px(t)表示人口普查时t年x岁人口数，l0/Lx(t)为生命表上出生人口活到x岁时的逆存活率。这样可以根据下面的公式来估计t年x岁人口Px(t)在出生时的人数，即：

(1)

因为三次人口普查标准时点都是11月1日0时，所以2000年普查时点上x岁人口与2010年x+10岁人口和2020年x+20岁人口为同一队列。如果要估计1992年11月1日到1993年10月31日出生队列的孩子数，在同一队列可以找到三个对应的数据，即2000年普查时7岁人口、2010普查时17岁人口和2020年普查时27岁人口。我们需要在这三个人口数中选一个“基准人口”，即相对更为准确的人口，依此来反推该队列的出生人口。

图1 跨越三次普查的人口出生队列图(注：横轴为出生时间，纵轴为年龄)

这样，出生队列可以分为三段(见图1)。一是估计2010年11月到2020年10月之间出生的人口，只能依靠2020年普查0-9岁的“一点数据”；二是估计2000年11月到2010年 10月出生的人口，可以在2010年普查和2020年普查找到“两点数据”；三是估计2000年10月之前的出生人口，可以借助2000年、2010年和2020年普查的“三点数据”。如果只有“一点数据”，该数据只能作为“基准人口”，如果有两点或三点数据，则需要从中确定一个“基准人口”。

确定基准人口将依据三个假设：(1)尽管普查时任何一个年龄人口都同时存在漏报和重报，但我们假定漏报的程度远远大于重报的程度；(2)同一队列两点数据之间的一致性程度越强，意味着数据越准确；(3)2020年第七次人口普查分性别和年龄人口数据的准确性程度好于2000年和2010年普查。

要想利用公式(1)来估计出生人口，还需要求出各个时间段上人口从0岁活到x岁、从x岁活到x+10岁和从x+10岁活到x+20岁的队列存活率。我们将参照国家统计局公布的全国分性别人口预期寿命，结合统计局公布的2000、2010和2020年分性别和年龄死亡率，以及联合国给出的(西区)模型生命表，估计出修正的三次普查生命表，并将相邻两次普查的生存人年数进行平均，作为普查间队列存活率的估计；将2000、2010和2020年生命表中0到x岁存活率作为普查时点前x年出生人口估计时使用的存活率。由于各时间段的“队列存活率”是间断的，我们通过回归将各段存活率进行整合后得出三个普查时点上出生人口活到x岁的逆存活率，并依此反推队列出生人口。

3 三次普查队列人口描述

按照同一出生队列在2000、2010和2020年三个普查时点上给出相应的分性别和年龄人口数(见表2)。在这里，201811-201910指的是从2018年11月1日到2019年10月31日出生的人口队列(其余类推)。

在全国人口处于封闭状态假设下，同一出生队列人口也是“封闭”的。如果每次普查涵盖完整、准确的全国分性别、分年龄人口，即不存在性别和年龄漏报、重报和错报的话，同一队列人口数量变化只受存活率的影响。因为存活率总是小于1的，所以队列人口数会随着时间推移、在经历各次人口普查时不断减少。这样的话，每个队列人口从出生到经历第一次普查时的x岁，到第二次普查时的x+10岁，再到第三次普查时的x+20岁，每一间隔存活率是可以计算出来的，而且各段存活率的乘积就是从出生到2020年x+20岁时完整队列存活率。然而，由于普查存在漏报、重报和错报，准确的存活率不能直接从历次普查分年龄人口数据中得出，但可以利用各次普查获得的死亡人口或死亡率，通过生命表的形式估计出来。

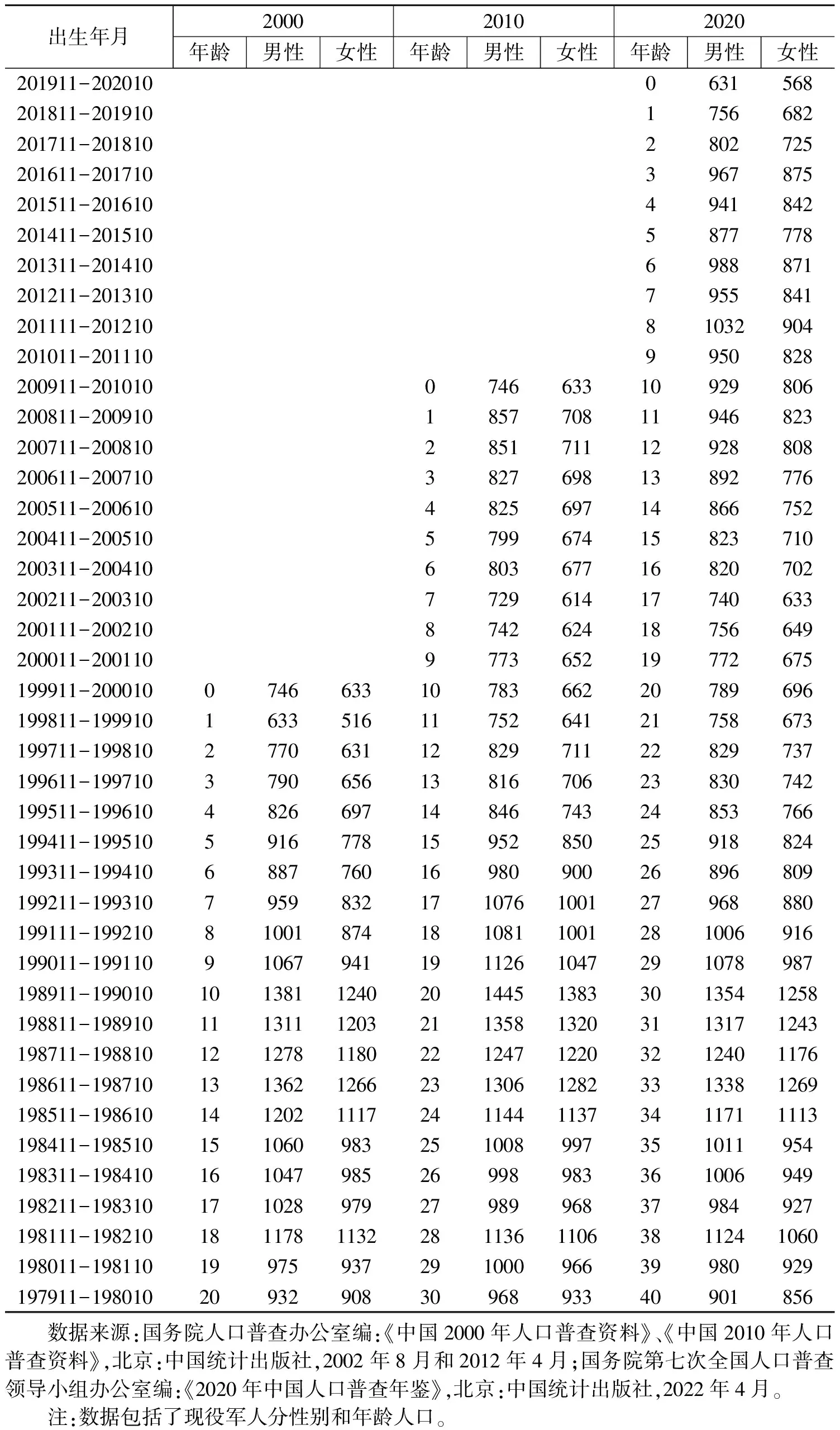
表2 按出生年月、普查年份、性别和年龄分的队列人口数(万人)

4 生命表存活率的估计

从人口普查中能够拿到的数据是分性别和年龄死亡率或存活率。使用三次普查给出的普查时点前一年全国分性别和年龄死亡率直接计算简略生命表，得出的分性别人口预期寿命与国家统计局公布的预期寿命差异很大(见表3)。这意味着普查登记的死亡人口有明显的漏报。为此，需要对死亡率进行调整，使其得出的预期寿命与国家公布的预期寿命尽可能一致。

生命表的具体调整方法是，将国家公布的分年龄死亡率与联合国发布的西区模型生命表(10)United Nations Population Division,https://www.un.org/development/desa/ pd/data/model-life-tables中预期寿命与统计局公布预期寿命对应的生命表死亡率进行比较，并计算各年龄组死亡率的相对差值，即：

死亡率相对差值 =(模型死亡率-普查死亡率)/普查死亡率

用字母表示为：

(2)

这里Dx表示x岁死亡率相对差值，Mx表示x岁模型死亡率，Sx表示x岁普查死亡率。

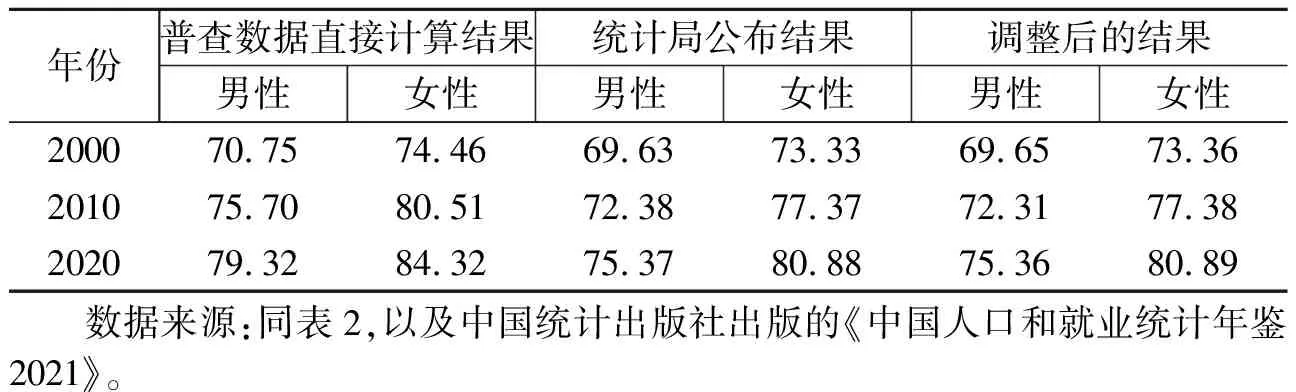
表3 直接计算、国家公布和作者估计的三次普查分性别预期寿命(岁)

对死亡率分两段进行调整，第一段是对低年龄死亡率调整，即0、1和5岁三个年龄，结合国家公布的当时婴儿死亡率和5岁以下儿童死亡率和模型生命表相应年龄死亡率进行调整；第二段对10岁以后各个年龄组的Dx进行拟合。在这里将确切年龄x作为自变量，死亡率相对差值Dx作为因变量，通过多个函数拟合(包括线性、对数、二次、三次、复合和增长函数)，选取确定性系数R2值最高的三次(cubic)函数作为拟合函数，计算分年龄死亡率相对差值的估计值(用字母dx表示)。再根据公式(2)，求出分年龄死亡率的估计值(用mx表示)mx=(dx+ 1)Sx，这个估计值得出的是确切年龄x=10、15、20、....、100岁的各年龄死亡率。

5 队列一致性系数和基准人口选取

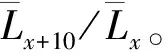
同样，根据表2给出的队列人口数，用同一队列后一次普查年龄为x+10岁人口除以前一次普查x岁人口，或用2020年普查x+20岁人口除以2000年普查x岁人口，我们称为“实际存活率”(12)这里的“实际存活率”并不意味着是真实的存活率，而是用实际数据、按计算存活率的方法得出的结果。。因为要计算实际队列存活率，同一队列必须至少有两个观测值，而2020年普查时0到9岁人口只有一个观测值，所以无法计算队列存活率。这样就只能计算2020年10岁以上人口队列的实际存活率。这样的话，2020年10岁到19岁队列每个队列可以计算一个实际存活率；2020年20岁及以上的每个队列可以计算三个队列存活率，一个是从2000年到2010年存活率，另一个是从2010年到2020年存活率，还有一个是2000年到2020年存活率(男性见表4，女性见表5)。

将实际存活率与理论存活率进行比较，可以做队列人口实际存活率和理论人口存活率的一致性检验，这里我们定义了“队列一致性系数”，它是用实际存活率除以理论存活率再减去1，具体计算公式为：

(3)

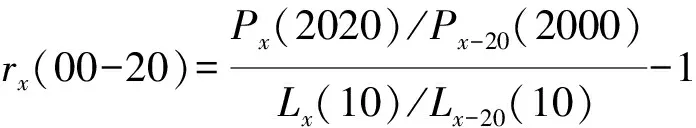
在这里rx值越接近0，意味着队列的一致性越好，离0的距离越远意味着一致性越差；如果rx大于0意味着后一次普查人数相对多一些，小于0意味着后一次普查人数相对少一些。

表4 男性按队列分的理论存活率、实际存活率和一致性系数

从经验上看，人口普查数据误差有以下几个特点：(1)婴幼儿漏报率比较严重，而且随着年龄增长漏报率会迅速下降，而且绝大多数漏报人口在10年后会出现(13)这里假定不存在流动人口的漏报。；(2)女性婴幼儿的漏报比男性婴幼儿更严重；(3)流动人口存在一定程度漏报，但随着登记对象的改变(14)这里指的是普查登记对象从2000年以前登记常住人口改为之后普查按现有人口和户籍人口同时登记。，2010年和2020年普查流动人口漏报率大幅度降低，特别是2020年普查流动人口几乎不存在漏报。流动人口年龄通常分布在16-52岁，30岁为最高值，如果存在漏报，会影响到这些年龄；(4)整体上看数据质量最好、漏报率最低的是2020年普查，其次是2010年普查，相对差一些的是2000年普查。

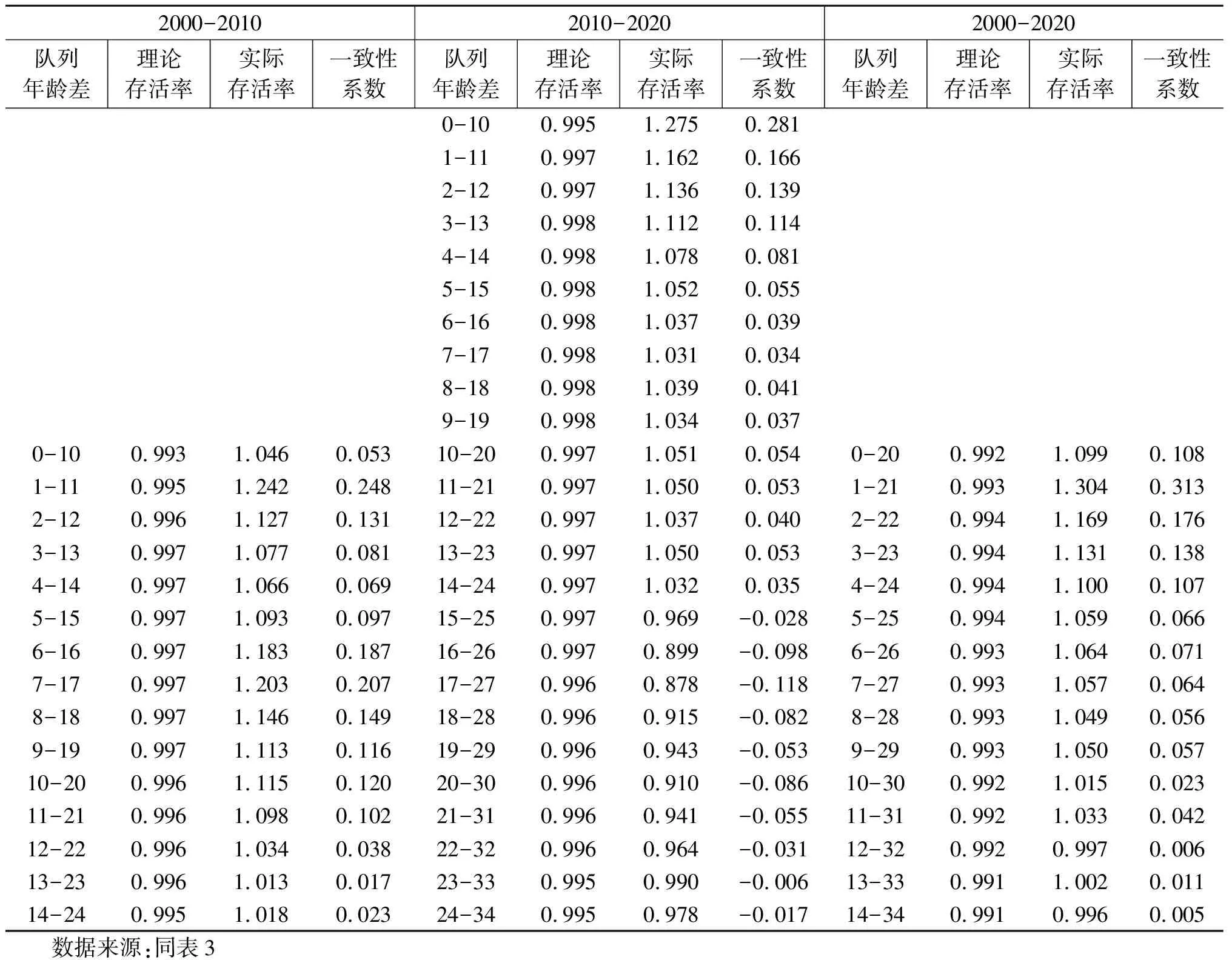
表5 女性按队列分的理论存活率、实际存活率和一致性系数

结合一致性系数和普查数据误差的特点，如果一致性系数为正值的，可以理解为前一次普查存在一定程度的漏报，因为后一次普查比前一次普查漏报率低，而且通常年龄越大漏报率越低(特别是婴幼儿阶段)，所以可以假定后一次普查数据是准确的。如果一致性系数为负值，基本上都是同一队列前一次普查人数多于后一次普查人数。产生这种情况往往比较难理解，也很难给出确切的判断。尽管认为后一次普查比前一次普查数据更准，但通常情况下前一次普查存在大量重报的可能性也并不大，此时很大可能还是后一次普查在这些年龄上存在漏报(15)这个判断只适用于一般情况，在特殊情况或特定年龄段也会出现前一次普查重报比较严重的情况。比如，2010-2020年男性15-25到21-31这7个队列和女性15-25到24-34这10个队列的一致性系数均为负值，或者说前一次普查人数明显多于后一次普查人数，这里很大可能是2010年普查相应年龄存在重报，而不是漏报。原因是如果看2000年到2020年男性5-25岁到11-31岁，女性5-25岁到13-34岁队列数据的一致性非常高，而恰恰2010年数据与相邻两次普查数据不一致，这说明2010年普查数据很大可能存在问题。。如果是三点数据，因为同一队列会有三个一致性系数，我们可以两两进行比较，做一致性的相互认证，这样一致性比较强的数据可能更为真实或准确。用队列一致性系数来检验同一队列不同时间上数据的一致性，最终目的是要判断哪个时点上的数据相对更准确一些，并将这个相对准确的数据定义为“基准人口”。在给定的假设下来判断数据漏报或重报，存在一定的风险。为了“安全”起见，我们设置多种可能性，即给出多个“基准人口”的选项。如果一个队列只有一个观测数据，则该数据本身就是基准人口。下面设定三类基准人口：

基准人口1：假定普查数据只存在漏报、不存在重报或漏报大于重报，那么在只有两个观测数据的同一队列上，如果一致性系数大于0，选择期末人口；如果一致性系数小于0，选择期初人口。若同一队列有三个数据，则选取一致性系数绝对值最大的；如果该值为正值则选期末人口、该值为负值选期初人口；如果只有一个观测数据，这个数据本身就是基准人口。基准人口1基本上是同一队列中人口数最多的那个数(16)理论上讲，存在最大数并不是基准人口的情况，但这种情况发生的可能性小，至少本数据中不存在。。

基准人口2：三个观测数据中的一致性最高(即一致性系数绝对值最小)的一对数据，如果系数大于0，取期末人口；系数小于0，取期初人口，基本上也是人口最多的的那个数；若为两个观测数据，同样是一致性系数大于0，选择期末人口；一致性系数小于0，选择期初人口，或取二者的最大值；一个观测数据的队列取该数据本身。基准人口2只是在针对三个观测点数据进行选取时，与基准人口1不一样。基准人口2实际上选出的是一致性最好的一对数据中数值最大的数。

基准人口3：以2020年数据为基准人口。这实际上相当于假定2020年数据最为准确的。

以上每一种基准人口选取方法对应一个估计结果，但三种方法里绝大多数的基准人口是一致的，只有个别队列是不一致的。针对不一致的基准人口，同一队列可以估计出不同的出生人口，这相当于存在一个“波动区间”，当然这不是统计意义上的置信区间。

6 队列出生人口的估计

6.1 估计的一般思路

同一出生队列只要选定一个基准人口，就可以通过逆存活率方法推出该对列出生人口，使用的一般公式为：

比如2010年5岁基准人口为Px(t)= P5(2010)，出生时人口为B(2010-5)=B(2005)。此时，逆存活率为100000/L5(2010)，出生人口计算公式为：

实际上，这里的0-5岁存活率L5(2010)/l0(2010)只是2010年生命表人口存活率，而不是队列存活率，因此将其作为队列存活率则存在一定的误差。

如果基准人口是2020年15岁人口，此时对B(2005)的估计公式就要改为：

同样道理，如果基准人口为2020年28岁人口，该人口在2000年为8岁，2010年为18岁，出生人口的估计公式为：

在这里，三个逆存活率中后两项均为两次普查生命表平均存活率，而第一项则是2000年普查存活率。之所以第一项用的是2000年普查存活率，而不是两次普查平均存活率的原因是本文并未估计1990年普查生命表。这是因为1990年普查时点为7月1日，与2000年普查时点11月1日不一致，所以1990年普查x岁人口与2000年普查x+10岁人口并不是同一队列，这样无法计算队列存活率。但是，这里用2000年普查数据计算逆存活率存在的一个最大问题是，反推的时间越长，存活率的误差也会越大。好在，后面我们会对这里计算出的逆存活率做进一步的修正。

这里还需要注意的是，三个逆存活率仍然是假定的队列存活率，而不是真实队列存活率。

6.2 逆队列存活率的估计

如果将2020年所有分年龄人口作为基准人口来反推出生人口，则需要计算2020年年龄为0-34岁人口从出生活到x岁的逆存活率l0/Lx，此时需要计算三个分段函数：

1.2020年年龄为0-9岁队列逆存活率 =l0/Lx(2020)，x = 0,1,2,....,9

2.2020年年龄为10-19岁队列逆存活率等于：

3.2020年年龄为20-34岁队列逆存活率等于：

把三段整合在一起就得到了2020年所有0到34岁人口从出生活到2020年时的逆存活率(见表6的计算值)。仔细分析逆存活率的变化会发现3段逆存活率并不是连续的，而是存在明显的跳跃或间断，这是因为我们是用三个普查年份生命表存活率得出的结果，而且三段逆存活率反映出了时期存活率的特点，即内部一致性很强，而外部一致性很差。为此，为了保证队列的一致性，我们用三次函数进行了拟合(见图2上面的两个图)，拟合效果也非常好，其中男性拟合函数的确定性系数为0.981，女性为0.971，并得出了拟合函数的估计结果。由于2020年生命表直接计算的0岁、1岁和2岁逆存活率队列结果和时期结果时间较近，所以差异不大，因此在估计的逆存活率中保留了计算值结果，而未采用估计值(见表6中2020年0-x岁逆存活率的估计值)。

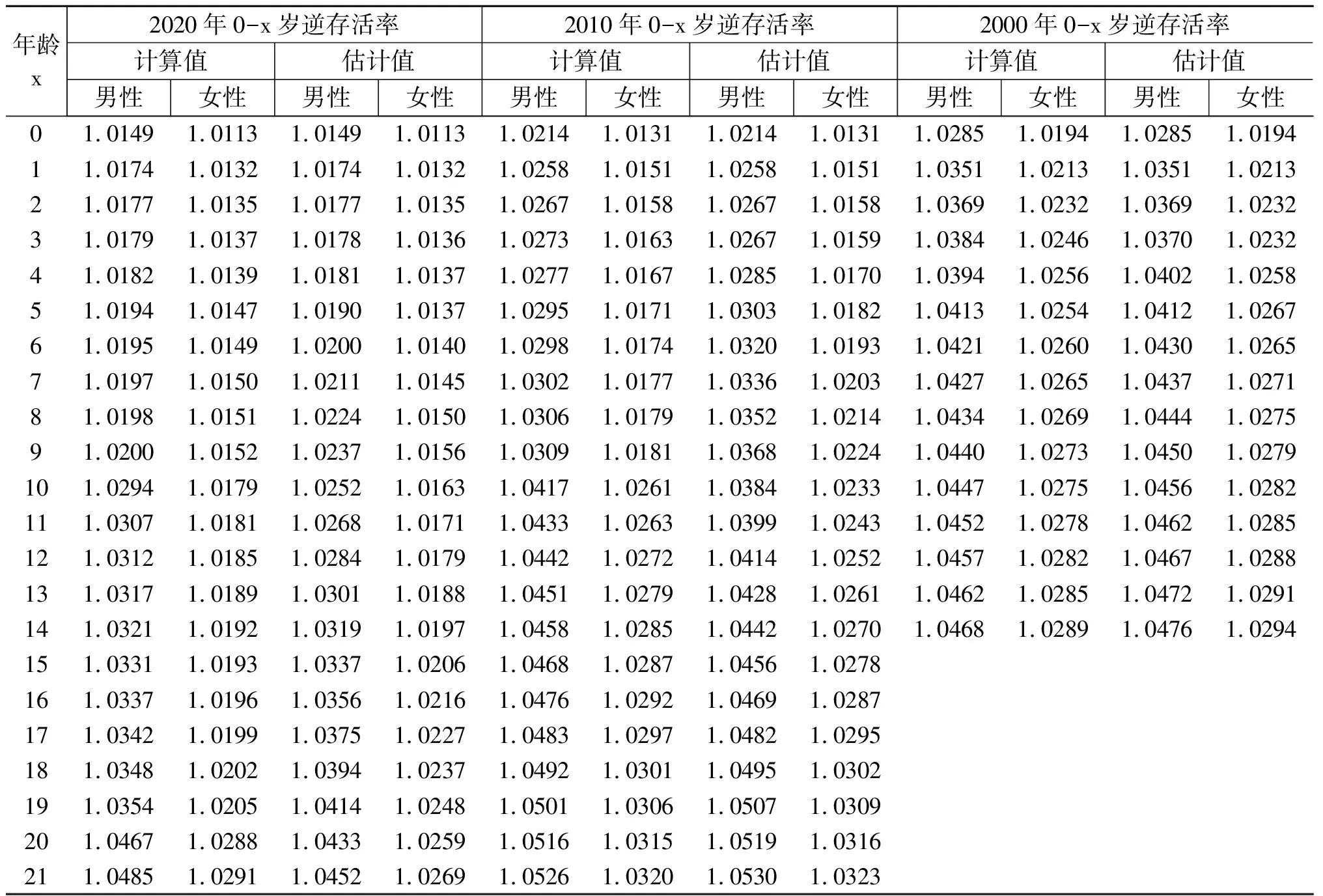
表6 从出生存活到三个普查年份相应年龄逆存活率的计算值和估计值

(续表6)

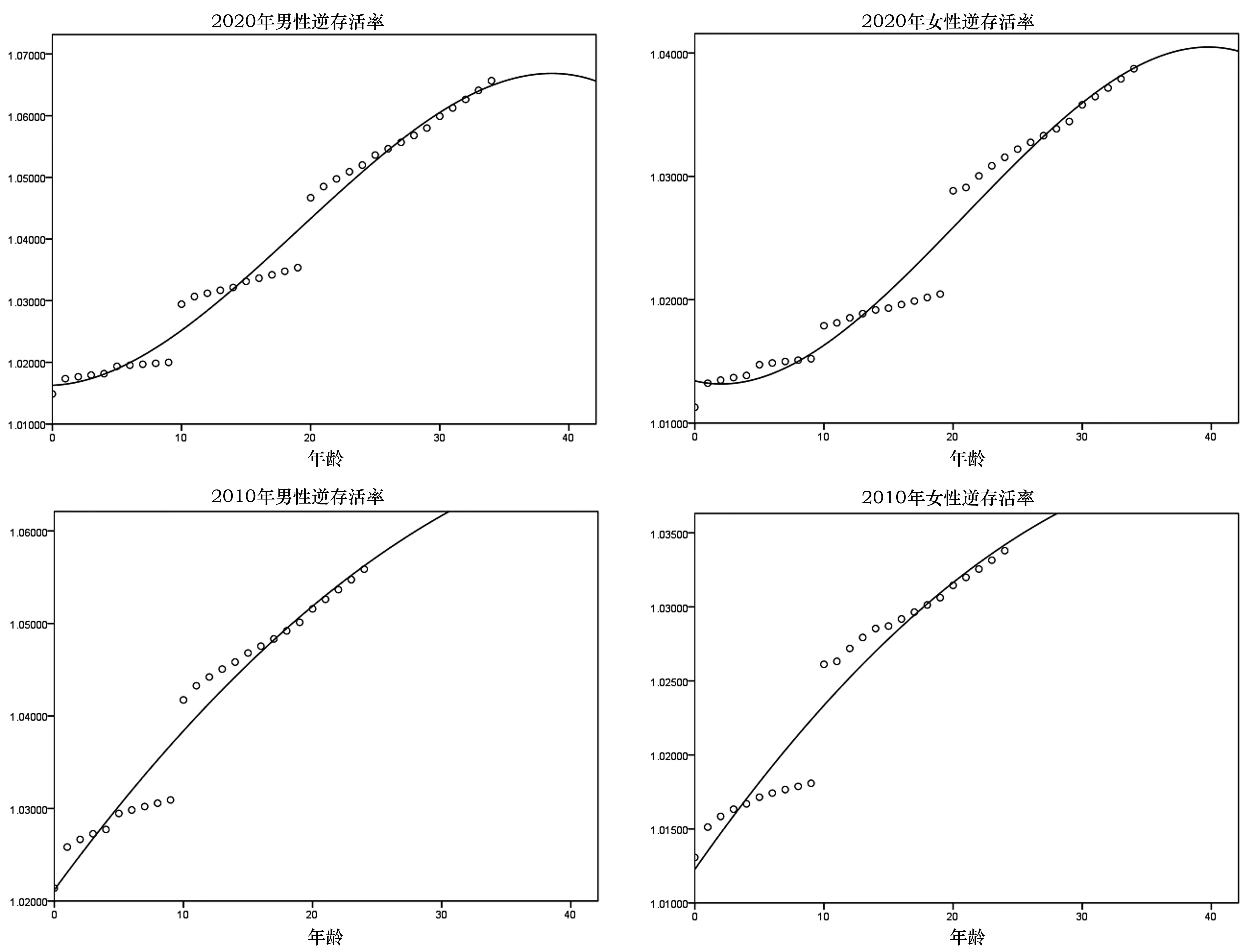
图2 按性别分的从出生存活到2010和2020年x岁的逆存活率拟合结果 数据来源：表6中的计算值

按照同样思路也得出了2010年各年龄人口反推出生人口时的逆存活率，点的分布同样存在间断。我们用二次函数进行了拟合(图2中下方两个图)，拟合得出的男性确定性系数为0.957，女性为0.940，并用拟合函数得出估计结果。同样在估计结果中保留了0、1、2岁的原始计算值。

如果用2000年生命表直接计算时期逆存活率，很明显它会与队列逆存活率存在差异，我们根据2010年的拟合结果，按照同样的相对增量调整了2000年的逆存活率，并将其作为队列逆存活率(见表6)。

6.3 队列出生人口的估计

根据以上给出的计算公式，一旦给定了基准人口和相应的逆存活率，就可以估计出所有队列的出生人口。表7给出的是按基准人口1估计的队列出生人口。表8给出的是按基准人口2和3估计的队列出生人口数，这里刨除了与表7相同的队列。

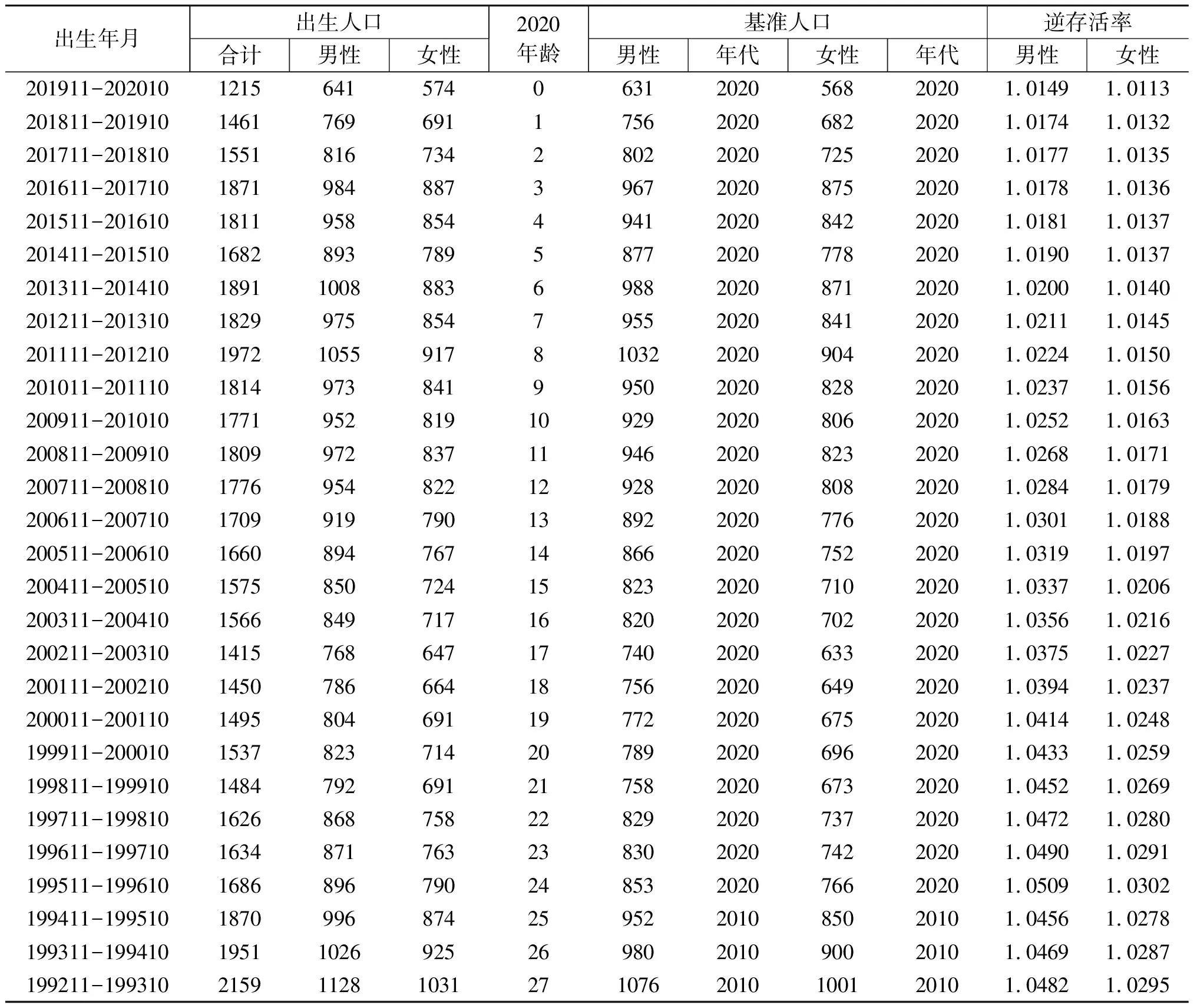
表7 按基准人口1估计的队列出生人口数(万人)

(续表7)

表8 按基准人口2和基准人口3估计的队列出生人口数(万人)

7 年度出生人口的估计

现在需要将队列出生人口转换为年度出生人口。转换的办法是将每一队列出生人口在前一年11月和12月份出生的人与在当年1月到10月份出生的人分离开来，然后将每个队列11月和12月出生人口与上一个队列同一年1月到10月出生人口合并，得到一个完整日历年出生人口。这里的关键是如何将11月和12月份出生的人从队列出生人口中分离出来。

图3 四次普查11和12两个月出生人口占一年内出生人口的比例(单位为1) 数据来源：中国统计出版社出版的1990、2000、2010和2020年《人口普查资料》

首先，给出1990、2000、2010和2020年四次全国人口普查出生人口在月份上的分布。在这里，2000、2010和2020年人口普查出生人口均为普查前一年11月1日到普查当年10月31日出生的婴儿，而1990年普查是1989年1月到12月的出生人口。根据这个数据分性别计算11月和12月出生人口占普查统计的一年出生人口的比例(见图3)。如果出生人口在一年内各个月份分布均匀的话，每两个月出生的人口应该占全部人口的1/6，即16.7%。很明显，11和12两个月出生占比明显高于平均占比，特别是2000年普查得出的这两个月出生人口占全部出生人口的四分之一还多。我们在这四个时间点上做线性内插得出这期间所有各日历年11和12月份出生人口所占比例。1990年之前几年的比例是用线性外推得到的。

根据估计出来的11和12月出生人口占比，将其应用到由基准人口1估计出的队列出生人口，按照日历年将其分解为前一年11和12月份出生人口和当年1到10月份出生人口两部分，然后再将同一年两部分人口相加，得到男性和女性全年出生人口(见表9)。

表9 按照日历年份和基准人口1估计的分性别出生人口(万人，%)

(续表9)

同样，针对基准人口2和基准人口3计算出分性别的队列出生人口。使用同样的分解比例，得到按日历年分的出生人口(见表10)。

根据以上的估计过程和假设，我们可以看出三个基准人口估计出的出生人口在1986-1995年期间存在一定的差异，在1995年以后是完全一致的。我们认为基准人口2估计出的结果更为可信，因为它是选择多点数据中一致性最强的数据作为基准人口。跟基准人口1相比，基准人口2估计出的出生人口数更少一些；跟基准人口3比，基准人口2和基准人口3估计出的结果差异也非常小(只有1992年二者相差的略多一些)。从估计结果的准确度看，对早期出生人口的估计，由于逆存活率时间跨度长，误差会更大一些，但因为同一队列有三个点数据可以做一致性认证，所以由此选取的基准人口更为准确；相反对近期出生人口的估计，尽管逆存活率误差小，但因为不能做多个数据的一致性检验，往往基准人口的不确定性会更大一些。好在本次普查数据准确性还是比较高，从而导致基准人口的偏差(特别是漏报)不会太大。

8 结果分析

为了方便将估计的出生人口与国家公布数据进行比较，表10也给出了官方公布的出生人口(17)这实际上是由官方公布的出生率推出的出生人口。，图4给出了官方公布的历年出生人口和按基准人口2估计的出生人口。从中可以看出，估计的出生人口从1986到1990年一直处在高位。尽管1990年第四次人口普查以后，官方已经大幅度上调了1980年代的出生率，但从估计的结果看，上调的幅度还远远不够，其中官方估计的1986到1988年出生人口比本文估计的出生人口少了100多万，1989和1990年少了200到300万人。正是由于1990年人口普查时才发现1980年代调查出生人口漏报率非常严重，最终导致统计局从1991年开始每年都大幅度上调出生率。

不幸的是，从1991年以后实际出生人口并没有像官方上调的幅度那样大，而是出现了大幅度下降，从而导致官方公布的出生人口大大高于本文估计的结果，其中1991年多出了73万，1992年多出了118万，最高值出现在1997年，当年公布的出生人口比本文估计的出生人口多了近400万。尽管学术界普遍认为，从1990年以后出生率和生育率都出现大幅度下降，而且统计局公布的出生率确实也表现出“大幅度下降”，但出生人口下降幅度如此之大，是我们之前没有预料到的。

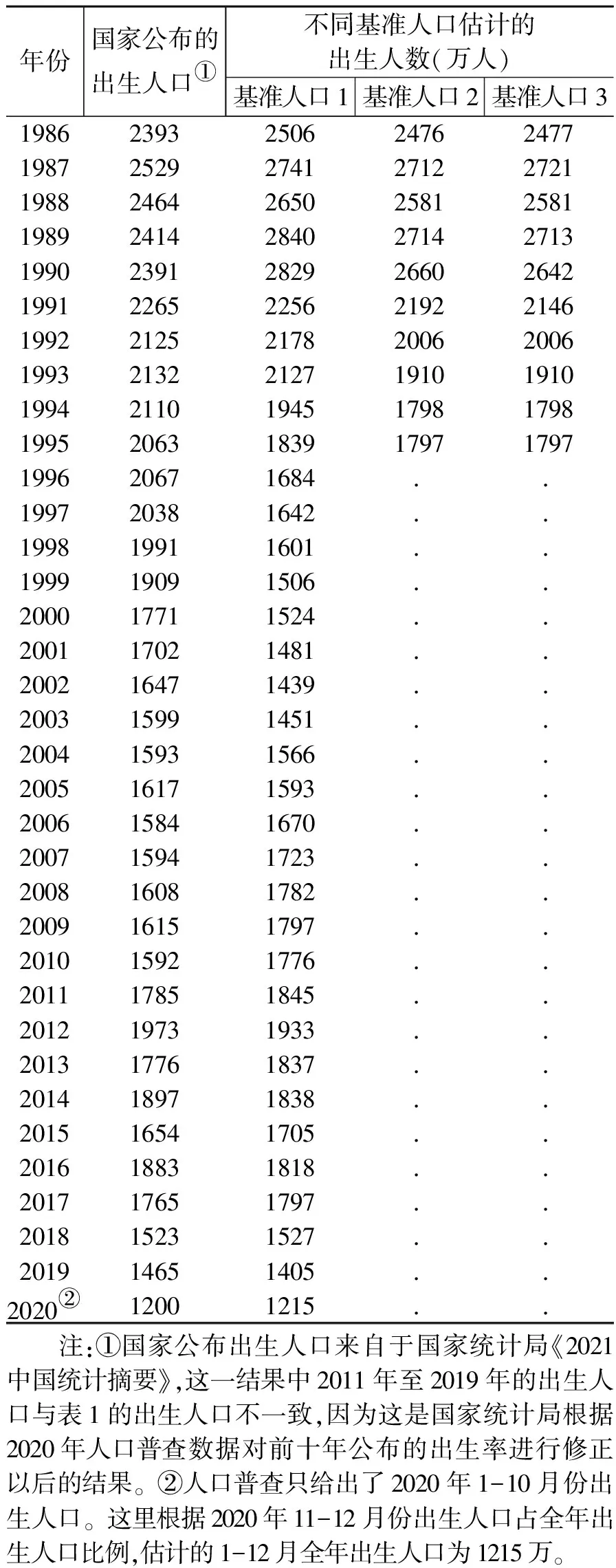
表10 按不同基准人口估计的1986-2020各年出生人口和出生性别比

图4 1986-2020官方公布的出生人口和按基准人口2估计的出生人口差异比较 数据来源：见表10

实际上，2000年普查结果可以证明这一点。2000年普查短表登记的出生人口为1412万人，统计局公布的出生人口为1771万人，如果当时认为统计局公布的数据是准确的，意味着人口普查出生人口漏报率为25.4%，这实际上表现出了官方对当时出生漏报水平的认识。本文估计的人数为1524万人，比实际登记出生人口多了112万人，比统计局公布结果少了247万。如果说本文估计的结果是准确的，则意味着普查出生漏报率为7.3%(=112/1524)。在这里，尽管官方公布的结果和本文估计的结果均比2000年普查登记的出生人口数要多，但官方给出的漏报率为20.3%，远远超出了“真实”的漏报率。

相对本文估计结果，从1991年到2000年的十年间，官方公布的出生人口累计多出了2688万人，这也进一步证实了2000年人口普查时全国总人口并不像公布的那样多，而实际登记人口数应该比公布的全国总人口数更为准确(18)2000年第五次全国人口普查主要数据公报公布的全国总人口为126583万人，而实际登记人口为124261万人，如果加上250万的现役军人人口，共计登记了124511万人(参见《中国2000年人口普查资料》编辑说明)。。从估计结果看，1991年到2005年国家公布的出生人口均高于本文估计的出生人口，这意味着在这15年的时间里，官方对出生人口数量一直存在着高估。有意思的是，从2006年开始则出现了对出生人口的低估，而且这种低估一直持续到2017年。表10给出的2011-2019年出生人口是官方在普查之后修正过的结果，而普查之前历年《国民经济和社会发展统计公报》公布的2011到2017年的出生人口(见表1)分别是：1604万、1635万、1640万、1687万、1655万、1786万、1723万，这些结果大大低于本文估计的结果。与本文估计的结果比，2011年少了240万，2012年少了近300万。而官方修正以后的结果与本文估计的结果相近。

总之，由于早期受计划生育工作、特别是“一票否决”制度的干扰，上世纪八十年代调查出生人口确实存在大幅度漏报，从而导致官方在公布出生数据前都会对调查结果做一些调整。从本文的估计结果看，1991年到2005年官方公布的出生率存在明显的高估，甚至影响到了2000年第五次全国人口普查总人口的准确性；从2005年以后则出现了明显的低估。2020年普查以后官方及时地对近十年来公布的出生率进行了调整，调整结果是合理的。从本文的估计结果中可以看出，从1990年以后，我们对人口形势一直存在着严重的误判。换句话说，如果我们真的当时就知道1990年后中国出生人口就已经出现了大幅度下降，生育政策的调整在那个时候就可能提到了议事日程，“二孩政策”在2000年之前就可能出台了。这意味着，政府调整生育政策至少晚了15年。