基于实物期权的电动汽车充电站投资决策评估研究
尚姗姗,刘敦楠,李晓宇,王文,刘明光,彭晓峰,杨烨
(1.华北电力大学经济与管理学院,北京 102206;2.国网电动汽车服务有限公司,北京 100033)
0 引言
在化石能源日益短缺和生态环境持续恶化的双重压力下,新能源汽车凭借其无噪音、低污染的优势吸引了不同国家政府的关注。截至2022 年1月,我国充电桩保有量为2.62×106台,其中包括公共充电桩1.18×106台、私人充电桩1.44×106台,车桩比约为2.31:1,尚未达到《电动汽车充电基础设施发展指南(2015—2020 年)》中设定的1:1 的目标。现有充电站容量难以满足用户日常充电需求,充电站充电桩的投资建设亟待发展。
目前针对电动汽车充电站的研究重点集中在充电站的选址与定容上。在充电站选址方面,高治佳等[1]基于充电距离和成本偏好构建了考虑已有充电站调整的电动汽车充电站选址模型。罗佳欣等[2-3]基于全社会经济成本和碳排放量构建了电动汽车充电站选址双层规划模型。在充电站定容方面,王妍等[4-5]通过研究区域交通流量与充电站投资建设的经济性,利用聚类算法确定了待建充电站的理想充电容量。刘新萌等[6-8]利用遗传算法对典型多站融合进行储能容量优化,设计了多站融合规划方案。张林垚[9]基于流量均衡原理建立充放电管理的快/慢充电站规划模型,实现了快充站与慢充站的优化配置。
由于充电站建设缺乏长期规划[10-11],对充电站进行投资决策分析可避免资源浪费与效益减少的问题,同时可以降低企业投资风险。目前针对投资决策分析的研究方法分为2 类:(1)传统投资决策方法,多为净现值法。王小胜等[12]基于净现值法提出节水效益分享型项目的投资风险评估模型,以实际试点项目验证了模型的适用性,缺点是仅考虑了货币的时间价值未考虑不确定因素影响的风险投资;(2)现代风险分析方法,多为实物期权法。李寅龙[13]利用实物期权理论中的B-S-M 定价模型较好地解释了互联网企业的价值。殷凤媛等[14-17]根据实物期权理论展开对增量配电网和变电站等投资价值的研究,验证了实物期权模型的有效性。
综上所述,本文针对电动汽车充电站投资较为粗放的问题,分析充电站投资收益模式及投资收益面临的不确定性,基于B-S 模型构建了充电量波动和充电站成本变动的波动率模型,最后通过算例分析证明了模型的有效性,为电动汽车充电站的投资决策提供重要参考。
1 电动汽车充电站投资效益及不确定性分析
1.1 电动汽车充电站收入
电动汽车充电站收入Y主要分为电量销售收入、服务费收入、政府补贴收入3 个部分。
1.1.1 电量销售收入
充电站运营的大部分收入来源于售电收入,售电收入一方面取决于充电站售电单价Psel,另一方面由用户的充电量Q决定。电量销售收入的表达式为:

式中:Yt,sel为运营商第t年电量销售收入;Pt,sel为运营商第t年售电单价;Qt为第t年用户充电量。
1.1.2 服务费收入
充电站运营商收取的充电服务费也是其收入之一,用来弥补设施运营成本。服务费收入表达式为:

式中:Yt,ser为运营商第t年获得的服务费收入;Pt,ser为运营商第t年收取的服务费单价。
1.1.3 政府补贴收入
目前我国大力推动新能源汽车充电设施建设,不同城市都有相应的补贴政策。政府一般按照运营商初始投资成本的一定比例给付补贴,其表达式为:

式中:Ysub为政府补贴收入;a为政府给予的补贴比例;Cin为初始投资成本。
由式(1)—式(3)可得充电站n年的收入现值为:

式中:PV(Y)为充电站收入Y的现值;i为行业收益率。
1.2 电动汽车充电站成本
电动汽车充电站成本C主要包括初始投资成本和营业成本2 类。
1.2.1 初始投资成本
初始投资成本Cin包括设备购置成本Cep、设备安装成本Cei、建筑工程费用Cce及其他成本Cot。其中Cep占Cin的比重较大,具体分为快充与慢充设备的购置成本。
1.2.2 营业成本
营业成本Ct,ru包括购电成本Ct,bu、管理成本Ct,ad、维护成本Ct,ma、土地租金成本Ct,la,其表达式为:

式中:Pbu为运营商购电单价;β为充电站管理费率;μ为充电站设施安装的维护费率。
由式(5)—式(8)可得充电站n年的成本现值为:

式中:PV(C)为充电站成本C的现值。
净现值ANPV是电动汽车充电站未来现金流量的折现,基于1.1 和1.2 节分析可得其表达式为:
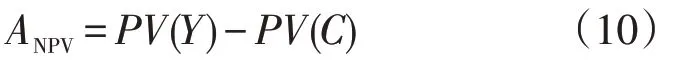
1.3 投资收益不确定性分析
由于电动汽车充电站投资成本较大、专用性强,其收益也更容易受到宏观和微观环境的制约。影响电动汽车充电站投资收益的不确定性因素[18]如表1 所示。

表1 影响电动汽车充电站投资收益的不确定性因素Table 1 Uncertain factors affecting the investment income of charging station
1.3.1 宏观环境的不确定性
1)经济。充电站行业与新能源汽车行业是资本密集型行业,受制于宏观经济周期的影响。如果未来宏观经济稳中向好,针对这2 个行业的投资会增加,反之则减少。
2)政策。从整个行业来看,充电基础设施补贴的强度会不断调整且存在一定时限,政府补贴退坡会较大程度影响充电站投资,导致充电站收益不及预期。
3)社会。受城市规划的影响,人口密度在各个区域的聚集程度不同,充电站在投资建设过程中需要将人口密度,作为判断投入规模与潜在收益的依据。
4)技术。现有技术无法彻底解决强光照、严寒风雨、明火汽油接触等条件引发的充电桩使用的安全问题。随着行业技术革新,现有安全问题将逐步解决,也必然会加速充电站投资收益增加的进程。
1.3.2 微观环境的不确定性
1)市场潜力。长期来看,新能源汽车保有量、充电站的建设数量都会导致车主充电需求发生改变和引起充电量波动,进而增加充电站收益的不确定性。
2)投资成本。由于直流充电桩(快充)的购置成本远高于交流充电桩(慢充),因此对于充电站而言扩大直流充电桩的建设规模会一定程度影响项目收益。此外,充电站建设用地的土地租金价格高低,也会影响项目收益。
3)运营效益。随着政府逐步重视电价机制改革以及电力价格的逐步放开,未来电价将参与市场竞争,成为不确定量。同理,服务费的制定也取决于同类充电站竞争引起的价格调整变化。这2 者变动都会直接导致充电站价值具有波动性。
基于1.3 节分析可知,电动汽车充电站项目收益存在多重不确定性,在具体投资决策中需要重视不确定性因素带来的附加期权价值。
2 电动汽车充电站投资实物期权模型
2.1 实物期权理论分析
基于实物期权理论,电动汽车充电站的第一阶段投资等同于购买基础资产的期权,具体衍生出5种主要的多重期权:扩张期权、延迟期权、收缩期权、放弃期权、转换期权。第二阶段的投资视充电站所处的宏观和微观环境而定。由于充电站的初始投资成本较大、运营年限较长且充电基础设施有很强的专用性,项目一旦开工建设极难撤销,具有不可逆性。根据现代决策理论可知:充电站项目投资过程中风险越大,经营管理者对项目的预期收益越高。而实物期权的定价方法可以较好地反映充电站投资项目未来价值的增长潜力,避免传统投资决策模型估值的局限性,故本文研究方法采用实物期权。
2.2 B-S模型
实物期权基本模型分为B-S 模型和二叉树模型。二叉树模型对步长的确定没有统一划分标准,人为划分容易造成偏差,影响期权价值的准确性。相较于二叉树模型,B-S 模型假设条件严格、推理严谨,所以本文采用B-S 模型开展研究。
一般对电动汽车充电站的投资分多个阶段进行,具体分为一期建设运营期阶段和二期充电桩增容等阶段。充电站增容依赖于用户的充电需求,经营管理者可根据用电需求增长率预测确定下一期投资时间和规模。当充电站运营获批后,充电站投资具有欧式看涨期权特性。B-S 模型表达式为:

式中:c0为充电站投资项目的期权价值;S0为未来充电站项目不考虑Cin的各年度现金流现值;N(D1)和N(D2)分别为标准正态分布下变量小于D1和D2时的累计概率;D1和D2为实数轴上的任意值;r为无风险利率;T为充电站投资项目的等待期;σ为充电站投资项目收益的波动率。
引入实物期权理论后,充电站的投资价值不仅要考虑其净现值,还要衡量项目不确定性带来的期权价值,充电站投资总价值(即项目扩展净现值)WENP为:

2.3 投资收益波动率建模
波动率关系着期权价值的准确性,是B-S 模型中的重要参数。波动率的常规计算方法有历史波动率替代、蒙特卡洛模拟、GARCH 模型预测等[17]。在传统的实物期权模型中,电动汽车充电站投资价值被设定为一个整体变量,其波动率也仅设定为一个输入参数而未进行深入探讨。下文将针对充电站投资的不确定因素进行波动率建模。
2.3.1 不确定因素建模
虽然充电站投资收益面临诸多的不确定因素,但充电站投资收益主要受制于充电量波动和充电站成本变动两个方面。
1)充电量波动。充电量波动是影响充电站投资收益的重要因素。随着新能源汽车保有量的逐年攀升和充电基础设施的逐步完善,未来用户的充电需求量将会激增。由于用户的充电需求量是一个随机过程,具有不确定性,因此本文假设充电量服从几何布朗运动[18-20],其表达式为:

式中:dzQ为维纳过程zQ的独立增量;εQt为服从(0,1)的正态分布随机变量;αQ和σQ分别为充电站充电量的漂移率和波动率。
2)充电站成本变动。考虑实际投资中的柔性决策,充电站会视经济发展情况、充电桩建设缺口、技术改进的情况来调整充电站扩建或是充电桩增容的投资,因此充电站的成本是随机变化的。假设充电站成本服从几何布朗运动,其表达式为:

式中:dzC为维纳过程zC的独立增量;εCt为服从(0,1)的正态分布随机变量;αC和σC分别为充电站投资成本的漂移率和波动率。
2.3.2 波动率建模
B-S 模型由布朗运动推导得到,充电站投资项目的收益波动率模型表达式为:

式中:γQC为充电量波动与投资成本变动的相关系数。
充电量与投资成本之间存在溢出效应,所以本文假设充电站投资收益与充电量及充电站成本之间存在正相关性。根据式(10),项目收益波动率可进一步表示为:

在期权模型中经常应用伊藤引理展开伊藤过程函数,几何布朗运动是一种简单形式的伊藤过程,该过程对时间连续但不可微。然而在期权定价过程中,需要对充电量波动函数和充电站成本变动函数进行求导[21]。为进一步求解式(16),需要根据伊藤引理将充电站投资价值的微分dANPV进行二阶泰勒展开。为简便运算,将ANPV简写为V,其表达式为:

忽略比dt更快趋于0 的项,整理式(17)可得项目价值的波动率,进一步表示为:

式中:m为残数。
3 算例分析
本文以浙江省某地级市G 公司典型区域充电站项目为例,将充电站选址位置划分为工业区、住宅区、商业区、风景区、公交区5 个区域[22-25]。以60 kW快充充电桩、7.5 kW 慢充充电桩的投资建设规划展开算例分析,选取2019—2031 年为“风险-收益”评估周期。
考虑设备的购置、安装与配电侧的投入等因素,充电站快充单桩与慢充单桩的初始投资成本分别为1.2 元/W,0.5 元/W,由于充电设施行业采用10 kV等级以下的大工业电价,所以评估周期内购电成本均取0.644 4 元/kWh。管理成本取充电站初始投资成本的6%并以每年3%递增,维护成本取初始投资成本的3%并以每年1%递增。此外,商业区建设充电站需要缴纳一定的土地租金,为简便计算计提当年10%的充电站收入归为土地租金成本。政府补贴以充电站初始投资成本的20%测算,平均服务费按照小幅下降的趋势收取。充电站建设参数如表2所示:

表2 充电站建设参数Table 2 Construction parameters of charging station
3.1 传统净现值测算结果
G 公司2019 年开展一期项目实际建设,分别在工业区、住宅区、商业区、风景区及公交区各投放了20,25,20,4,4 个60 kW 快充。由于电动汽车各年充电需求量不同,所以每年各区域充电桩利用率、平均充电费用和平均充电服务价格也有所异同,各区域充电站指标变化如图1 所示。

图1 各区域充电站指标变化Fig.1 Index changes of charging stations in each region
由图1(a)可知,前期工业区的充电桩利用率增长缓慢,经过用电引导后利用率会高于住宅区、风景区和公交区;受停车位的限制,商业区充电桩利用率会显著高于其他各区;住宅区受车主晚间时段充电需求影响,充电桩利用率较低;风景区与公交区充电桩利用率较为稳定。图1(b),图1(c)反映了在测算周期内,G 公司对各区域平均充电费增长和平均充电服务费下降的预期。
根据充电设施行业收益率10%测算,一期投资如表3 所示。

表3 一期投资Table 3 Phase I investment 元
由表3 可知,只有住宅区的ANPV远小于0。按照传统刚性的投资决策方法,应该停止对住宅区充电站的二期扩容投资计划。但随着住宅区电动汽车的数量增加和用户充电量需求上升,在住宅区投资充电站可能带来额外的期权价值,所以在投资过程中需要进行柔性决策。
G 公司认为公交区投放的充电桩基本满足充电需求无须再追加投资。项目计划在2020 年追加投资开展二期建设,分别在工业区、住宅区、商业区、风景区投放20,30,20,5 台60 kW 快充充电桩,建设期为1 年,评估周期为2021—2031 年。二期投资如表4 所示。

表4 二期投资Table 4 Phase II investment 元
由表4 可知,商业区充电站的ANPV值最大。虽然住宅区充电站初始投资高于其他3 个区域,但ANPV值较小。为此,本文将进一步分析4 个区域充电站的实物期权价值。
3.2 实物期权测算结果
由于σQ,σC参数的市场样本较难获取,因此以G 公司提供的同类型充电站运营数据为基础测算参数。区域波动率测算结果如表5 所示。

表5 区域波动率测算结果Table 5 Calculation results of regional volatility
由表5 可知,在工业区和商业区投资充电站项目风险最大,风景区投资充电站项目风险最小。根据式(11)、表4 和表5 可得4 个区域充电站的实物期权价值和WENP值,如表6 所示。

表6 实物期权价值Table 6 Project real option value 元
由表6 可知,在商业区和工业区投资充电站的期权价值最大,住宅区充电站的期权价值是风景区的3 倍。4 个区域的WENP值存在较大差距,实物期权法测算结果如图2 所示。

图2 实物期权法测算结果Fig.2 Calculation results of real option method
由图2 可知,对比4 个区域充电站项目的看涨期权价值,商业区的WENP值最大,可扩容建设。工业区和风景区在规模电动汽车的渗透率下同样具有追加投资的潜力。而大规模快充成本降低了住宅区充电站投资效益,导致住宅区的WENP值小于风景区。因此本文进一步优化住宅区充电站二期投资场景,改为全部投放慢充。住宅区充电站投资优化前后对比如表7 所示。

表7 住宅区充电站投资优化前后对比Table 7 Comparison before and after investment optimization of charging station in residential area
由表7 可知,将住宅区充电站二期投资更换为慢充投资策略时,WENP实现大幅度增长。这是由于慢充的初始投资成本远低于快充,住宅区充电桩利用率偏低,如果全部投放快充,易导致总体效能下降,相反快慢充结合可以有效实现车主的需求,减少公司投资成本。
3.3 敏感性分析
为进一步展现表6 中不同区域充电站WENP对项目波动率变化的反应程度,对项目波动率上下调整10%,20%,且考虑表7 中住宅区充电站投资优化前后的两种投资策略,以横坐标轴O 处的WENP为基准值,观测不同波动率下的WENP变化情况,波动率对不同区域WENP的敏感性分析如图3 所示。

图3 波动率对不同区域WENP 的敏感性分析Fig.3 Sensitivity analysis of volatility to WENP in different regions
由图3 可知,快充住宅区充电站WENP对项目波动率的变化最为敏感,当波动率增加20%时,其WENP增加逾10 万元,具有高风险高回报特征,但需要警惕的是快充建设成本高、投资回收长;而快慢充组合的住宅区充电站WENP呈现刚性,抗风险能力强,能够给公司带来稳定的经济效益;风景区的充电站WENP相比于工业区、商业区会更容易受到项目波动率的影响,但前后WENP差距较小,说明风险承受能力较大。
商业区、工业区、风景区的一期项目投资蕴含了后续投资机会,会带来实物期权价值,在这3 个区域建设充电站且全部投入快充充电桩,项目可获得较好的盈利能力。综合权衡效益与风险后,对住宅区充电站投资采取一期投入快充、二期投入慢充的策略更加符合经济性,采用实物期权法对G 公司充电站项目进行投资决策更具有现实意义。
4 结语
本文在研究电动汽车充电站项目投资时,通过分析充电站投资的多重不确定性因素,结合布朗运动原理考虑了充电量和投资成本的不确定性,构建了基于B-S 模型的充电站投资价值评估模型,以此形成对充电站投资的实物期权价值及扩展净现值的综合评估,有效弥补了传统方法测算充电站投资价值的不足。但由于政府补贴政策和技术革新带来的风险价值较难量化,本文未将以上2 点放入模型中,为提高投资决策精度,后续可以考虑开展政策与技术这2 类不确定性因素对充电站投资收益影响的量化研究。

