基于SSA-VMD-SE-KELM结合蒙特卡洛法的风电功率区间预测
韦 权,汤占军
(昆明理工大学信息工程与自动化学院,云南昆明 650504)
0 引言
随着风电在电网中的渗透率逐年上升,风电的强波动性、强随机性对电网的调度决策和安全运行造成了难以克服的挑战[1]。降低与风力发电相关的复杂性和不稳定性,能够给电力系统的统筹调度提供可参考的方案[2]。
近些年来,国内外很多专家学者把研究重点聚焦于风电功率点预测的研究,点预测方法主要分为物理研究法和统计研究法[3]。物理法主要是利用数值天气预报(Numerical Weather Prediction,NWP)信息和风场详细的地理地貌信息,通过功率曲线映射得到功率预测值,预测结果的准确度受到NWP 精确度的影响。统计法是基于历史风电统计数据,通过参数估计、数据训练、曲线拟合等方式建立风电功率与影响因素之间的联系,常见的方法有支持向量机法[4]、神经网络法[5]、灰色模型法[6]、时间序列法[7-8]、人工智能法[9]等等。归因于风力资源的不稳定性以及预测模型自身的局限性,当前风电功率点预测结果为电网调度等实际应用提供的帮助不多。
为满足决策者在电网调度、可靠性评估等方面的需要和探索可定量表现出风电功率波动范围的新预测形式,研究人员们开始把目光转移到风电功率区间预测研究。风电功率区间预测相较于点预测,可更直观地反映风电功率的起伏趋势。文献[10]提出一种将BiLSTM 与Bootstrap 方法相结合的风电功率区间预测模型。文献[11]提出将径向基神经网络作为预测模型,再结合分位数回归法构造功率预测区间。文献[12]提出了一种基于混沌鸡群优化和极限学习机的风电功率区间预测模型。文献[13]提出了一种基于朴素贝叶斯的正态指数平滑法和混合滑动核密度估计的组合风电功率区间预测方法。文献[10-13]各自以不同的研究角度丰富了风电功率区间预测的方法,但是鲜有针对降低原始风电功率序列的波动性、随机性来提升风电功率区间预测的精准度。
为了有效降低原始风电功率序列的复杂程度,提出一种基于参数优化VMD-SE-KELM 结合蒙特卡洛法的风电功率区间预测模型。首先引入麻雀搜索算法(Sparrow Search Algorithm,SSA)优化变分模态分解(Variational Modal Decomposition,VMD),将原始风电功率序列分解为理想数量的子序列,再根据计算出的样本熵(Sample Entropy,SE)对其进行序列重构,得到的新子序列分别建立核极限学习机(Kernel Extreme Learning Machine,KELM)点预测模型,叠加各点预测结果得到最终点预测结果及功率误差序列,最终使用蒙特卡洛法对误差累计概率密度随机抽样得到对应置信度下的预测区间。通过实例进行验证,结果表明本文所提方法可以保证预测区间的准确性、可靠性。
1 风电功率点预测模型建立
1.1 变分模态分解算法
现实中采集到的风电功率数据存在强波动性、强非线性、强不稳定性、强时间依赖性等不利因素,直接输入预测模型往往难以得到准确的预测结果。为了提高预测精度,可对功率序列使用VMD对预测输入数据进行预处理。
VMD是由Konstantin Dragomiretskiy和Dominique Zosso 于2014 年提出的一种完全自适应、非递归的信号分解算法。它的作用是将输入信号v(t)分解成若干个特征、频段互异且带宽有限的本征模态函数(Intrinsic Mode Function,IMF)序列,目的是在所有模态之和等于输入信号v(t) 为前提下,使所有IMF 带宽总计最小[14]。变分模型如下:

式中:uk={u1,…,uk} 与ωk={ω1,…,ωk} 分别为VMD分解出来的K个子模态集合和其对应的中心频率集合;∂t为求偏导运算符;*为卷积运算符;δ为单位脉冲函数;j 表示虚数。
引用惩罚因子α以及Lagrange 乘法算子λ(t)的目的是把带约束的变分问题转化为无约束的变分问题,这样方便成为Lagrange 表达式的推广形式。为了便于求得变分问题最优解,用交替方向乘子法迭代计算出各IMF 及其对应的中心频率。
大量实验和理论研究告诉我们,影响VMD 算法分解效果优劣的主要参数包括分解出的子模态个数值K以及惩罚因子α。使用VMD 算法自适应地处理目标信号时需要提前设置好分解参数[15]。
1.2 麻雀搜索算法
SSA 作为近年较新颖的群智能优化算法,它的提出灵感源于麻雀群的捕食行为和反捕食行为[16]。此方法相较于鲸鱼优化算法[17](Whale Optimization Algorithm,WOA)、粒子群算法[18](Particle Swarm Optimization,PSO)、灰狼优化算法[19](Grey Wolf Optimizer,GWO)等传统智能优化算法具有不依赖梯度信息、寻优精度较高、稳定性较强等优势,广泛运用于机器学习、深度学习等研究领域[20]。
SSA 在寻优的过程中,把麻雀群分成3 部分,分别是观察者、跟随者及警戒者。麻雀群中视野位置比较好的麻雀为观察者,数量一般占种群的10%~20%,任务是带领同伴辨认安全方向和搜索食物,跟随者则会跟随观察者一起争夺食物,观察者和跟随者之间可以相互转换。同时,任意分配10%~20%的麻雀为警戒者,任务是发现周围环境的威胁,并会释放警告信号提示种群成员往安全的区域移动。
观察者位置更新变化如下:

式中:c为目前的迭代次数;M为最大的迭代次数;为迭代次数为第t次时,第i只麻雀的第j个维度的位置;a为范围[0,1]的随机数;R2为预警值,R2∈[0,1] ;ST为种群的安全阈值,ST∈[0.5,1] ;L为一个所有元素为1 的1×d阶的矩阵;Q为一个服从正态分布的随机数。
当满足R2<ST时,表示此刻麻雀种群身处在安全的区域内,四周并没有发现捕食者,故观察者可以扩大食物的搜索范围,带领种群获取更多的食物;当满足R2≥ST时,表示此刻种群内已经有警戒者发现周围出现了捕食者,并且发出了危险警告,随之麻雀种群作出反捕食行为,即观察者迅速带领种群成员调整觅食位置,转移到安全区域。
跟随者的位置更新变化如下:

当满足i>n/2 时,表明第i个适应度较低的跟随者没有争夺到食物,此时为了摆脱饥饿状态,飞往其他区域进行觅食。
警戒者位置更新变化如下:

式中:β为控制步长的参数,是一个服从于均值为0 并且方差为1 的正态分布的随机数;为迭代到c次时的全局最优位置;K1为一个属于[-1,1]的随机数,用于控制麻雀移动的方向;fi为目前麻雀个体的适应度值;fω为全局最劣的适应度值;fg为全局最佳的适应度值;ε为一个无限接近于0 的常数,为避免式子分母为0。当满足fi>fg时,该个体处于群体的边缘区域,极易遭受攻击,为了躲避攻击,要向种群中心靠拢。
1.3 样本熵
近似熵是一种量化时间序列复杂度的重要标准,却因为算法自身的缺陷而往往导致结果欠佳。样本熵(SE,无量纲)作为近似熵的一种改进算法,其本身具备良好的鲁棒性和一致性,且算法本身不依赖于数据长度,可以减少近似熵产生的误差[21]。样本熵值越小,序列的自我相似性越高;反之,序列的复杂性就越高。本文依照样本熵对VMD 分解后得到的IMF 序列加以重构处理,提高序列重构的解释性。针对给定序列,其样本熵的计算步骤及参数设定见文献[22]。
1.4 核极限学习机
极限学习机(Extreme Learning Machine,ELM)是由Huang 等人于2006 年提出的一种新型单一隐藏层前馈神经网络,具有拟合速度快、非线性拟合能力强、网络易实现等优点[23]。KELM 是针对ELM 算法的一种改进,它基于ELM 算法加入了核函数,以达到增强ELM 算法的稳定性、泛化性的目的。传统ELM 算法表达式为:

式中:N为样本个数;ω为输入层到隐藏层之间的权值;b为隐藏层的偏置;H为神经网络的隐藏层矩阵;H+为H的广义逆矩阵;β为隐藏层与输出层之间的输出权重;g()为激活函数;k为隐藏层的神经元个数;T为预测目标值向量。
KELM 通过引入核函数,将ELM 算法中的随机映射变成了稳定的核映射,同时加入参数I/C至单位对角阵(HHT)中防止其特征根为0,I为一个N阶单位阵,C为正则化系数,需要预先设置。提高ELM 的稳定性和泛化性。综上所述,KELM 算法表达式如下:

式中:k(a,b)为核函数,一般设定为径向基核函数,需要设置核函数参数。
1.5 基于SSA优化的VMD
选取VMD 算法参数的不合适,很可能导致目标信号的过分解或欠分解,造成信号分解的效果欠佳。单纯凭借经验来选取分解参数,如保持一个参数不变优化另一个参数或者随机设置2 个参数,结果往往会产生较大的误差。本文利用SSA 对VMD算法中重要的2 个参数,即惩罚因子α和分解出的子模态个数K进行寻优,来提升VMD 算法结果的精度。图1 为SSA-VMD 流程图。

图1 SSA-VMD流程图Fig.1 SSA-VMD flow chart
1.6 基于SSA-VMD-SE-KELM点预测
针对现实风电功率波动性强、随机性强的问题,本文将VMD 分解算法、KELM 模型相结合,提出了一种基于SSA-VMD-SE-KELM 风电功率点预测模型,此模型可有效提升风电功率预测的精度和可靠性。具体建模过程如下:
1)对原始风电数据进行预处理,包括剔除异常数据补充缺失数据等。
2)为了防止不同量纲之间的差异对模型结果带来的误差,对各个输入量进行归一化,并把数据集按照8:2 的比例划分为训练集和测试集。
3)针对训练集风电功率序列,利用SSA 算法优化对VMD 算法,最终确定VMD 分解的最优参数。
4)利用VMD 分解风电功率序列,得到若干个IMF 序列。
5)计算各个IMF 序列的SE 值,SE 值相近的IMF 序列进行重构,得到若干个新序列。
6)若干个新序列分别于其余变量一起输入设置好的KELM 模型训练学习。
7)各个预测结果叠加得到最终点预测结果。
2 风电功率区间预测模型建立
2.1 蒙特卡洛法
蒙特卡洛法也叫做统计模拟法,是一种采用随机抽样统计来估算的计算方法[24]。它的基本思路是利用已知目标函数y=f(x1,…,xn)对随机变量(x1,…,xn)进行概率分布估计,对这些变量进行随机抽样得到对应的y的特征值,通过大量抽样结果计算得出y的概率分布。随着抽样模拟次数的增多,蒙特卡洛法计算的结果与实际结果的误差越来越小[25]。针对蒙特卡洛法而言,最重要的是对一个(0,1)的概率分布进行随机抽样统计,利用误差统计分析得到的累计概率密度函数正是一个在(0,1)上的概率分布,这为使用蒙特卡洛法建立预测区间提供了理论上的支持。
2.2 基于SSA-VMD-SE-KELM 结合蒙特卡洛法的区间预测模型
针对现实风电功率的不稳定性以及点预测自身的局限性,本文将VMD 分解算法、KELM 模型和蒙特卡洛法相结合,提出了一种基于SSA-VMDSE-KELM 结合蒙特卡洛法的风电功率区间预测模型,此模型可有效提升风电功率预测的精度和可靠性。图2 为具体预测建模流程图。

图2 区间预测模型结构图Fig.2 Interval prediction model structure diagram
3 实例分析
本文采用云南某风电场2 号风机实际采集到的风电历史数据,采集时间为2020 年9 月至10月,时间间隔为10 min,将历史数据划分为训练集和测试集,对其风电功率进行点预测和区间预测。
3.1 评价指标
对于风电功率点预测结果,本文采用平均绝对误差(Mean Absolute Error,MAE)和R-Square(R2)这2 个无量纲指标来考量点预测的精准度,MAE 的值(EMA)越小,R2越大,则点预测的效果越好,模型精度越高。评价指标定义式如下:

式中:M为预测点的数量;Pi为第i个时刻风电功率的实际值;i为第i个时刻风电功率的预测值;Pˉ为M个风电功率的平均值。
对于风电功率区间预测结果,本文采用预测区间的覆盖率(Prediction Interval Coverage Probability,PICP)和预测区间平均宽度(Prediction Interval Normalized Averaged Width,PINAW)来考量预测区间的优劣,二者无量纲。PICP 的值(IPICP)用于评判预测区间的可靠性,其值越大越好,PINAW 的值(IPINAW)用于评判预测区间的清晰度,其值越小越好。定义式如下:

3.2 点预测结果与分析
风电功率序列具有较强的波动性和不平稳性。对原始风电功率序列进行VMD 分解,同时用SSA优化VMD 算法中的参数K和α。经过多次试验,SSA 的参数设置如下:最大迭代次数为50 次,种群大小为30,K的寻优范围为[3,100],α的寻优范围为[7,5 000],适应度目标函数为样本熵极小值。采用SSA 最终得到VMD 的最优参数为K=7,α=3 000,故利用VMD 算法将原始风电功率序列分解成7 个IMF子序列。
为了有效降低建模的复杂程度,计算出各个IMF序列的样本熵,并将样本熵相近的子序列合并成为新的子序列。各个IMF序列的样本熵值见图3。

图3 各子序列样本熵值情况Fig.3 Entropy value of each subsequence sample
可明显看出,子序列中IMF3,IMF4,IMF6,IMF7的样本熵值相近,说明它们序列复杂程度相近,所以把它们合并成一个新的序列。此时重构后得到的新的子序列记作K1,K2,K3,K4:

然后再采用KELM 分别对新的子序列K1,K2,K3,K4进行点预测,KELM 参数具体设置为:正则化系数C=4 000,核函数参数为3.9。最后,将每一个子序列KELM 点预测结果叠加得到最终的功率预测值。
为了说明SSA-VMD-SE-KELM 模型的有效性,本文采用经验模态分解(Empirical Mode Decomposition,EMD)与KELM 相结合的模型(即EMD-KELM),VMDKELM,SSA-VMD-KELM 3 种点预测模型与之对比。图4 为各个点预测模型的预测结果对比,表1为各个点预测模型的评价指标。
由图4 可以看出,相较于其他预测模型而言,SSA-VMD-SE-KELM 模型的预测结果曲线明显更贴合真实值的曲线。由表1 可以更直观地发现,相较于其他的预测模型而言,SSA-VMD-SE-KELM 模型的各项点预测评价指标均优于其他预测模型,R2达到了0.970 5,EMA降至2.741 4。本文提出的SSAVMD-SE-KELM 点预测模型可见预测结果极佳,具有较高的预测精度。
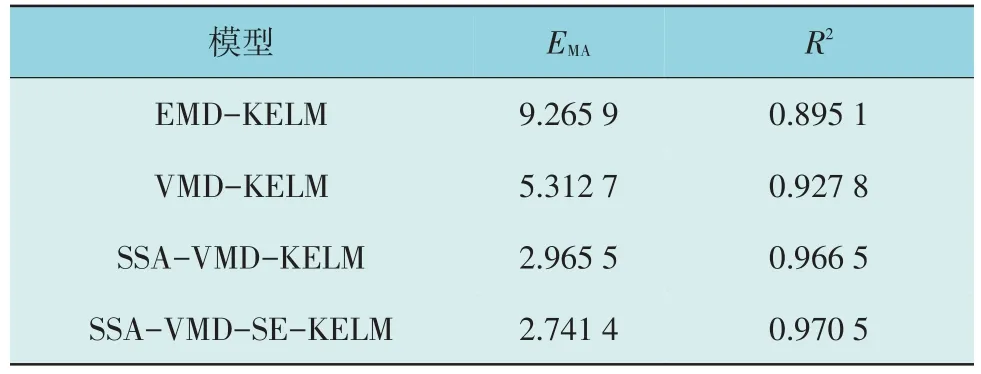
表1 各个点预测模型的评价指标Table 1 Evaluation index of each point prediction model

图4 各个点预测模型的预测结果对比Fig.4 Comparison of prediction results of each point prediction model
3.3 区间预测结果与分析
利用SSA-VMD-SE-KELM 点预测模型的预测结果,与真实值作差便得到得到预测误差功率序列。经过多次试验,本文选择使用高斯分布拟合预测误差序列得到误差累计概率密度分布函数,然后采用蒙特卡洛法对累计概率密度进行1 000 次随机抽样,根据抽样累计概率密度得到所对应的误差序列,按照采样累计概率密度的大小对采样误差序列重新排序。最后给定置信度,结合点预测结果得出该时刻对应的预测功率区间。图5 为各置信度下的预测区间结果。

图5 各置信度预测功率区间Fig.5 Predicted power interval of each confidence level
为了更好地证明本文提出的模型之优劣,分别计算出SSA-VMD-SE-KELM 模型与蒙特卡洛法、Bootstrap 重采样法、分位数回归法、核密度估计法结合计算出区间预测评价指标,对比结果见表2。

表2 各预测区间评价指标Table 2 Evaluation indicators for each prediction interval %
表2 可以看出,在相同置信度下,相较于其他3种模型,本文提出基于SSA-VMD-SE-KELM 结合蒙特卡洛法的区间预测模型,可以做到紧密地跟随着风电功率序列的变化趋势,并且可以得到更高的区间覆盖率及更窄的区间平均宽度。例如在置信度85%区间里,PICP 的值为89.98%,相较于其他3种方法,指标分别提升了3.46%,4.86%,4.75%;PINAW 值也是最小的,相较于其他3 种方法,指标分别降低了3.63%,7.79,5.01%,体现模型效果的高准确性、高可靠性。
为了进一步证明本文提出的模型有效性,采用甘肃某风电场1 号、3 号、5 号风机的历史风电数据对模型效果进行验证。图6 为各风机置信度为85%时的预测功率区间效果。

图6 各风机置信度85%预测功率区间Fig.6 Predicted power range of each fan with confidence level of 85%
表3 为各风机预测功率区间评价指标。实验结果不难看出,本文提出的基于SSA-VMD-SE-KELM和蒙特卡洛法的区间预测模型在其他数据集上的效果准确度、可靠度较为出色,预测区间均能得到优秀的区间覆盖率和较窄平均宽度。

表3 各风机预测区间评价指标Table 3 Evaluation index of each fan forecast interval%
4 结论
由于风电功率固有的强波动性和强随机性,以及目前点预测方法难以实现风电功率预测结果的高精准度,本文提出了一种基于SSA-VMD-SEKELM 结合蒙特卡洛法的组合区间预测模型。通过算例结果分析,可得到以下结论:
1)经过参数优化后的VMD 算法分解,再结合样本熵对其子序列进行重构,可有效降低风电功率序列的复杂程度,提升风电功率点预测结果的精度。
2)本文提出的预测模型可以有效地实现风电功率区间预测。相比于其他传统模型,可以更加紧密地跟随着风电功率序列的变化起伏趋势,得到更高的区间覆盖率及更窄的区间平均宽度,为电网的安全运行和调度决策提供更多的可参考方案。

