双碳目标下基于分解-集成的月度煤电需求预测研究

高 恬，牛东晓，纪正森，斯琴卓娅

（1.华北电力大学经济与管理学院，北京 102206；2.新能源电力与低碳发展北京市重点实验室，北京 102206）

0 引言

2020 年，习近平总书记提出中国力争在2030年前实现碳达峰，2060 年前实现碳中和，为促进我国能源电力高质量发展提供了根本依据。2021 年以来，煤炭价格猛涨以及能耗双控目标的约束，给火电厂造成了巨大压力。随着光伏、风电等可再生能源大规模接入电网，其发电的随机性、波动性使供电特性发生了变化。为保障我国能源安全供应、推动能源转型，对煤电行业“保发展”和“降碳”提出了更高的要求。为了指导未来能源转型过程中煤电的生产从而保障生活生产，对未来月度煤电需求进行提前精准预测的重要性日益突出。而煤电需求受到多种因素的影响，给中期预测带来了极大挑战。

负荷预测的模型主要包括统计学方法和机器学习方法。统计学方法主要有时间序列法[1-2]、回归分析法[3-5]等，但该方法较简单，不适用于非线性负荷序列。所以目前更多的研究使用机器学习模型，主要包括极限学习机模型（Extreme Learning Machine，ELM）[6]、神经网络模型（Neural Network，NN）[7-9]、支持向量机模型（Support Vector Machine，SVM）[10-11]等。文献[12]通过大量实验证明了ELM 模型在计算准确率和速度上优于SVM 和BP 神经网络。基于机器学的预测模型效果关键在于参数的选取[13-14]，但是粒子群算法[15]和灰狼优化算法[16]容易出现过度收敛，麻雀搜索算法（Sparrow Search Algorithm，SSA）性能优于上述2 种算法，在一定程度上避免过度收敛的问题。基于此，本文建立SSA-ELM 预测模型。

随着研究的深入，学者们发现结合数据分解技术和机器学习算法的组合预测方法成为更多学者的研究重点[17-22]，如集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）[23]等。文献[24-25]分别通过小波包分解和EEMD 分解负荷，提高了预测精度。但是小波包分解的效果依赖于小波基函数的选择，EEMD 模型的噪声大小和集成时间需要人为设置，缺乏可靠性。奇异谱分析作为无参数自适应方法，适用于研究非线性、复杂的时间序列，具有较强的降噪能力，目前已经应用到预测中[26]。

本文提出了一种基于改进奇异谱分析（Improved Singular Spectrum Analysis，ISSA）和麻雀搜索算法优化极限学习机（SSA-ELM）的月度煤电需求预测模型。首先，通过改进奇异谱分析将原始序列进行分解重构，并采用SSA-ELM 模型对重构序列进行预测，最后叠加得到煤电需求预测结果。最后以江苏省月度煤电数据为例，结果表明ISSA-SSAELM 模型的预测精度较高，具有较好的适用性。

1 模型算法介绍

1.1 改进奇异谱分析

奇异谱分析是研究非线性时间序列数据的一种非参数方法[27]。它基于一维时间序列构造轨迹矩阵，对矩阵进行分解和重构，提取原始序列的不同分量信号，如趋势、周期、噪声等，然后分析不同分量序列的结构，完成进一步的预测。改进奇异谱分析（Improved Singular Spectrum Analysis，ISSA）在SSA 的基础上，引入奇异熵对其进行改进，达到了在分组过程中去除原始序列中噪声信息的目的[28]。

1）嵌入

长度为N的一维时间序列YN=(y1,y2,…,yN)，设定窗口长度，将原始时间序列进行滞后排列得到轨迹矩阵X：

2）奇异值分解

对轨迹矩阵进行奇异值分解。求矩阵XXT的特征值，得到L个特征值λ1≥λ2≥…≥λL≥0 和各特征值对应的特征向量U1,U2,…,UL。

定义

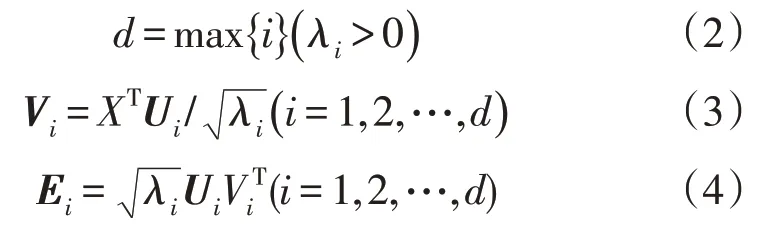
式中；Ei为基本矩阵；矢量Vi为主成分；λi为特征值；Ui为特征值λi对应的特征向量。

则轨迹矩阵的奇异值分解可以表示为：

3）基于奇异熵的分组

引入奇异熵对噪声分量进行判断，具体公式为：

式中：k为奇异熵的阶数；SEk为k阶的奇异熵；ΔSEi为奇异熵在第i阶上的奇异熵增量。

基于奇异熵理论，当奇异熵增量在某一阶之后较小且降幅平缓时，该阶之后的奇异值视为噪声部分。如果奇异熵的增量在第m阶趋于稳定，则从第一阶到第r阶的奇异值主要包含有效信息，随后的奇异值与噪声有关。

在此基础上，对分解的序列进行重构，选取前r个Ei近似X，并划分为p组I1,I2,…,Ip，代表不同的趋势成分，将每个组内的矩阵相加得到新的矩阵XIj，则轨迹矩阵X可以近似表示为：

4）对角平均

式中：u为[1,N]之间的整数。

1.2 麻雀算法优化的极限学习机预测模型

1.2.1 极限学习机

为了提高效率并减少前馈神经网络中的训练瓶颈，Huang 等人提出了一种网络模型ELM[12]，具有前馈互连，但只有一个中间层，具有随机初始权重，在迭代过程中不需要更新，计算速度较快。ELM 能够逼近任何连续、非线性、可微和有限函数[29]。ELM模型包括3 层：输出层、隐含层和输入层。图1 显示了ELM 模型的结构。

图1 ELM结构图Fig.1 ELM structure diagram

如图1 所示，ELM 模型包含输入层、隐含层和输出层：输入变量为N个，输出变量为N个。对于含有N个样本的数据集(Xj,Yj)，F(x)为激活函数，隐含层节点为l，ELM 模型表示为：

式中：Yj为第j个输出层神经元的输出；ωi为连接输入层和隐含层节点的权重；bi为隐含层节点的阈值；βi为连接输出层和隐含层节点的权重。

ELM结构写成矩阵形式为：

式中：H为隐含层节点的输出；β为输出权重；Y为期望输出

1.2.2 麻雀搜索算法优化极限学习机

在煤电需求预测领域，参数对于模型的预测精度有很大影响，优化效率低将导致模型的不完善和预测能力差。而由Jiankai Xue 等人[30]于2020 年提出的麻雀搜索算法（Sparrow Search Algorithm，SSA），具有收敛速度快、稳定性好等优点，其灵感来源于麻雀种群的觅食和反捕食行为。所以本文引入SSA模型用于ELM 模型的参数优化。

SSA 中有3 种麻雀：发现者、加入者、侦察者。发现者负责寻找食物丰富的区域，加入者利用发现者寻找食物，侦察者负责在捕食者出现时会发出警告信号。在每次迭代中，发现者的位置更新如下：

加入者位置更新如下：

侦察者位置可表述如下：

式中：为第t次迭代中发现者的最佳位置；β为步长控制参数，是服从（0，1）正态分布的随机数；K∈[-1,1] 是一个随机数；ε为一个很小的常数。fi，fb和fw分别为第i个麻雀、最佳麻雀和最差麻雀的适应度值。fi＞fb意味着麻雀处于群体的边缘，fi=fb表明群体中最好的麻雀意识到危险。

SSA 优化ELM 参数的步骤如下：

1）初始化相关参数；

2）计算麻雀种群个体适应度；

3）得到当前最佳位置，最差位置和最差适应度；

4）根据式（9）、式（10）、式（11）更新发现者、加入者、侦察者的位置，并更新适应度；

5）判断终止条件，若满足则输出当前最优个体和适应度；

6）利用输出的最优参数计算输出权值矩阵。

1.3 ISSA-SSA-ELM混合模型预测框架

ISSA-SSA-ELM 组合模型对煤电需求的预测主要包括3 个部分：

1）序列分解：对煤电需求序列进行奇异谱分析，从而将原始序列分解为多个子序列，并利用奇异谱熵对奇异谱分析进行改进，从而识别并去除噪声成分，并将前r个成分重构为趋势序列和周期序列，将r+1到L个成分重构为噪声序列。

2）序列预测：将重构后的趋势序列建立考虑经济环境因素影响的SSA-ELM 预测模型，对周期序列应用SSA-ELM 模型进行预测，有效提高各序列的预测精度。其中，麻雀搜索算法优化极限学习机的步骤如1.2.2 所示，从而得到具有最优参数的SSA-ELM 模型。

3）预测结果重建与评估：将各序列得到的预测结果叠加，得到最终的煤电需求预测值。并采用均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、决定系数（R-Square，R2）以及运行时间t来评估预测模型的性能。RMSE 的值用ERMS表示，MAE 的值用EMA表示，MAPE 的值用EMAP表示。误差指标值计算公式如下：

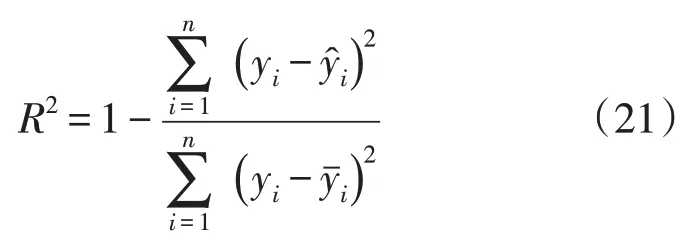
式中：yi为实际值；为预测值；为实际值的平均值；n为样本数。

本文所提出的ISSA-SSA-ELM 混合月度煤电需求预测模型流程如图2 所示。

图2 ISSA-SSA-ELM混合模型预测流程图Fig.2 Flow chart of ISSA-SSA-ELM hybrid model prediction

2 算例分析

本文选取江苏省2011 年1 月—2019 年12 月煤电月度数据作为历史数据对所提出的模型进行验证，考虑到经济发展以及双碳目标的能源转型需要，选取了经济环境相关因素作为序列的影响因素，包括GDP、SO2排放量、CO2排放量这3 类数据，数据来源于国家统计局和江苏统计局。

由于3 个影响因素的统计周期均为季度或者年度统计，所以本文通过Eviews 10 应用插值法对该类数据的月度空缺值进行填补。

2.1 改进奇异谱分析结果

在奇异谱分析中，窗口长度L的选取会影响分解的效果，从而影响预测结果，L的选取应该不超过序列长度的1/3，通常取周期的整数倍。本文L取24（周期数为12），根据式（5）计算各分量对应的奇异熵增量（无量纲），结果如图3 所示。图4 展示了SSA 分解得到的24 个分量中的前9 个分量，横坐标为年月。

图3 奇异熵增量曲线图Fig.3 Plot of singular entropy increments

图4 ISSA分解得到的前9个分量Fig.4 The first 9 components obtained from ISSA decomposition

结合图3、图4 可以看出，从第16 阶开始，奇异熵增量曲线逐渐平稳，累计贡献率仅为4.2%，所以前15 个分量包含了原始序列有效信息，第16—24个分量视为噪声分量，将其去除。第1 个分量对应的奇异熵增量最大，第1 个分量清晰地反映了煤电需求曲线的变化趋势，所以将第1 阶重构为趋势序列。第2—15 阶对应着周期成分，将2—15 阶奇异值重构为周期序列。重构得到的趋势、周期序列如图5 所示。从图5 可以看出，重构后的趋势序列，说明应用ISSA 对煤电需求曲线进行分解在获得序列主要特征的同时，可以有效地提取趋势和周期序列，并去除噪声分量。

图5 重构序列图Fig.5 Reconstructed sequence diagram

2.2 预测结果分析

本文所有预测模型均在Matlab R2018b 版本环境下进行。基于公平原则，设各模型中的SSA 最大迭代次数为100，种群规模设置为20，发现者和意识到有危险麻雀的数量分别占70%和20%，预警值为0.6；ELM 隐含层节点个数设为20 个，隐含层函数为Sigmoid。

对于趋势序列，将趋势序列作为因变量，GDP、SO2 排放量、CO2排放量作为自变量，将2011 年1月—2018 年12 月共96 组数据作为训练集，2019年1 月—12 月共12 组数据作为测试集，应用SSAELM 模型进行预测。对周期序列序列，取2011 年1月—2019 年12 月共108 个数据作为训练集，2020年1 月—12 月共12 个数据作为测试集，应用SSAELM 模型进行预测。ISSA-SSA-ELM 模型的最终预测结果如图6 所示。

图6（a）为应用SSA-ELM 对趋势、周期序列分别预测得到的曲线，6（b）为将2 个重构序列的预测结果进行叠加得到的最终预测结果曲线。可以看出ISSA-SSA-ELM 模型的预测精度较高，模型具有良好的泛化能力，说明ISSA 算法可以对复杂序列进行有效分解并去除噪声分量，SSA-ELM 模型能够对非线性序列进行较好地模拟，所以ISSA-SSAELM 模型能够很好地跟踪复杂序列的变化，得到精度较高的预测结果。

图6 ISSA-SSA-ELM组合模型的预测结果Fig.6 Prediction results of the combined ISSA-SSAELM model

2.3 对比方法分析

为了进一步验证本文方法的有效性，用经验模态分解（Empirical Mode Decomposition，EMD）与SSA，ELM 结合，即EMD-SSA-ELM 模型，将EMDSSA-ELM，SSA-ELM，ELM，SVM 作为对比模型对江苏省2019 年的月度火力发电量进行预测。采用ISSA-SSA-ELM，EMD-SSA-ELM，SSA-ELM，ELM，SVM 5 种模型得到的煤电需求预测结果如图7 和表1 所示，5 种模型的误差结果及运行时间对比如图7和表2 所示。可以看出5 种预测模型都能较好对煤电需求进行预测，其中ISSA-SSA-ELM 模型的预测误差最小，具有较高的预测精度。

图7 多种方法的预测结果曲线Fig.7 Prediction result curves for multiple methods

表1 多种方法的预测结果比较Table 1 Comparison of prediction results of multiple methods 100 GWh

表2 多种方法的预测结果评价对比Table 2 Comparison of prediction results evaluation of multiple methods

一般来说，ERMS，EMA，EMAP越小，R2越大，说明拟合结果越好。通过对比5 种模型的误差指标值可以看出：ISSA-SSA-ELM 模型的ERMS，EMA，EMAP值最小，R2值最大，说明本文提出的模型预测精度最高。具体来看：

1）ISSA-SSA-ELM，EMD-SSA-ELM 模型的ERMS，EMA，EMAP均小于SSA-ELM，ISSA-SSA-ELM模型的ERMS，EMA，EMAP，较SSA-ELM 模型分别降低22.7%，21.2%，17.6%。EMD-SSA-ELM 的ERMS，EMA，EMAP较SSA-ELM 模型分别降低19.2%，12.6%，10.5%，虽然ISSA-SSA-ELM 模型和EMDSSA-ELM 模型的运行时间大大超过单一预测模型，但是经过分解重组后，对每个子序列进行SSA-ELM模型预测的运行时间更短，说明本文对复杂、非线性序列进行分解是有效的，分解后的子序列复杂性更低，可以大大提高预测精度。

2）ISSA-SSA-ELM 模型的ERMS，EMA，EMAP均小于EMD-SSA-ELM，ERMS，EMA，EMAP分别降低4.3%，9.9%，8.0%，而且ISSA-SSA-ELM 模型的运行时间比EMD-SSA-ELM 模型少0.69 s，说明ISSA 分解效果比EMD 模型更好，运行效率更高，能够更加快速且有效地分解原始序列并去除噪声影响，提升预测模型的精度，同时使用EMD 模型也难以对原始序列的趋势、周期、噪声序列进行有效识别。

3）SSA-ELM 模型预测误差小于ELM，SVM 模型，且SSA-ELM 算法的运行时间仅比ELM 算法多1.96 s，比SVM 算法多1.52 s，但是优化模型精确度却有了很大提升，说明应用SSA 对ELM 模型的参数进行优化，有效地提高了ELM 模型的预测精度和稳定性。

根据所有模型的对比可知，本文提出的ISSASSA-ELM 模型的预测精度最高，对于复杂、非线性序列的预测具有一定的适用价值。

3 结论

双碳目标是我国能源转型新目标，鉴于煤电在保障电力能源可靠供应和推动能源转型中的“压舱石”作用，研究月度煤电需求预测对于未来指导煤电发展具有重要意义，但是月度煤电需求变化具有非平稳性、非线性的特点，应用单一的模型进行预测具有局限性，很难准确预测未来煤电需求的变化。所以本文将改进奇异谱分析引入到电量预测领域，并提出了麻雀搜索算法优化极限学习机的参数，建立了ISSA-SSA-ELM 混合模型，为月度预测提供了一种切实可行的方法。得出的主要结论如下：

1）应用改进奇异谱分析模型对煤电需求序列进行分解，并利用奇异熵识别噪声成分，实现非线性复杂序列转化为具有不同变化特征的子序列，能够显著提高煤电需求预测精度。

2）麻雀搜索算法全局搜索能力强，收敛速度快，为极限学习机模型提供了一种新的参数优化方法，显著提高了ELM 模型的预测精度和稳定性。

3）本文以江苏省2011 年—2019 年的月度煤电需求为例，算例表明，ISSA-SSA-ELM 模型能够识别原始序列中的噪声成分，提取其中的趋势、周期序列，并应用SSA-ELM 模型对不同序列分别进行预测，将趋势、周期序列的预测结果叠加得到最终的预测结果，相较于其他混合模型，预测精度更高，适用性更好。

本文提出的分解-集成预测方法有效地提升了预测效果，但也存在一定的局限性。首先，本研究仅分析了GDP，CO2，SO2排放量对双碳目标下煤电需求的影响，需要考虑更多的外部因素；其次，随着影响因素日益复杂，确定性的负荷预测能够提供的信息具有很大局限性，下一步可以应用区间预测对煤电需求进行分析以获得更多有效信息；最后，在预测方法部分，由于数据量的限制，本文选择了极限学习机模型，未来可以在更多样本的条件下应用深度学习技术，进一步提高模型的预测精度。