双碳及能源安全背景下中国电煤月度需求组合预测

成润坤，岳赛雅，张国维，侯赛，刘达

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学智慧能源研究所，北京 102206）

0 引言

双碳目标下，绿色能源的供应比例越来越高，其不确定性对电力能源稳定供应造成较大的压力。火电具有较高的可控性和稳定性，因此，火电在保障电力系统能源安全供给中发挥着重要作用。

未来长时间内火电仍将是我国电力供应的主要形式[1]，燃煤发电在我国火力发电中一直占据主导地位[2]，电煤的供给情况决定火电的生产。2021 年我国多地“拉闸限电”主要源于电煤供应不足[3]。在能源和经济频繁波动下，为避免因煤炭供应阻塞导致的发电动力不足或燃煤过度积存致使电厂成本增加，亟需及时精准感知电煤需求，以保障电力生产计划顺利执行，及电力供给安全。

目前关于电煤需求预测的研究相对较少，主要集中于煤炭总需求的预测。在影响因素方面，仅陈梦等[4]分析了宏观政策、运力和价格对电煤需求的影响。大部分学者从煤炭总需求的角度分析了经济增长、能源消费结构、产业结构、煤炭供给[5]、能源加工转换效率[6]、煤炭利用效率、能源替代效应[7]、煤炭价格、煤炭产量和总人口[8]等因素的影响。基于相关研究，本文采用格兰杰因果检验（Granger Causality Test，Granger）从大量宏观经济及能源生产因素中挖掘显著影响电煤需求的指标，以用于预测。在预测方法上，有学者采用系统动力学仿真模型[9]、改进X-12-ARIMA 模型[10]、单时序ARMA 和多元协整回归模型[11]等预测电煤需求量，但现有部分模型存在缺乏客观性、忽略外部因素影响、非线性信息感知弱等问题。

近年来，深度学习在诸多领域成功应用[12]，但在电煤需求预测中的应用较少。相比传统时间序列模型，神经网络可以更好地描述复杂的非线性问题，预测精度更高，可靠性更强[13-14]，包括反向传播神经网络（Back-propagationNeural Network，BP）[15-16]、循环神经网络（Recurrent Neural Network，RNN）[17]、长短期记忆网络（Long Short-term Memory，LSTM）[18-20]、门控循环单元网络（Gate Recurrent Unit，GRU）[21]等。BP 模型可有效探索变量间的非线性关系，但容易陷入局部最优，收敛速度慢[22]；LSTM 模型可以有效解决“长期依赖”问题，但参数多、且易陷入过拟合[23]；GRU 模型利用较少参数即可保证预测性能，但不能充分挖掘非连续特征在高维空间中的联系[24]。组合预测模型可以综合多种方法所提供的信息，以此提升预测精度[25-27]。本文提出一种基于BP、LSTM和GRU 模型的组合模型充分挖掘电煤需求序列信息，预测我国电煤月度需求，该模型可以有效融合3个子预测模型的优点，提升预测能力。

现有关于电煤的月度需求研究较少，主要分析了煤炭年度需求，其数据频率低，且预测可信度和实用性不足。为更加精准感知电煤需求，本文收集大量月度经济及能源生产数据，采用格兰杰因果筛选显著影响电煤需求的变量，构建不同提前期范围的数据集。然后用BP，LSTM 和GRU 模型分别构建基于不同数据集的预测模型进行预测，并使用回归加权不同模型得到组合模型。最后对比单个模型最优预测结果与组合模型预测结果，验证本文所提预测模型的可行性和有效性。

1 相关研究方法

1.1 Granger变量筛选

Granger 用来检验一个时序变量是否对预测另一个时序变量有显著意义[28-29]，在分析变量影响关系方面得以广泛应用。其基本观点是：未来的事件不会对目前与过去产生因果影响，而过去的事件对现在及未来产生影响。即Granger 具有一定的“预测”能力。为预测电煤需求，本文应用格兰杰因果探索特征变量和电煤需求间的影响关系及其提前期。

与传统的相关关系检验相比，格兰杰因果关系不仅能检验变量之间是否存在影响关系，同时也能分析变量之间影响的时序关系，这一特点使得该方法在预测领域变量筛选和提前期设置中得到普遍应用。

1.2 BP模型

BP 是一种按照误差反向传播训练的前馈网络。其核心思想是利用梯度搜索技术，使实际输出值和期望输出值的误差均方差最小，常被用于预测领域。主要包含前向传播和误差反向传播2 个过程。信息从输入层输入，经过隐藏层非线性变化，产生输出值。若输出值与期望输出值误差未满足要求，则将误差信号反向传播，据此调整网络权重，直至满足误差要求[30]。但该算法学习速度慢，容易陷入局部极小值。

1.3 LSTM模型和GRU模型

LSTM 模型是一种时间循环神经网络，解决了一般循环神经网络存在的长期依赖问题，改善了RNN 模型梯度爆炸和消失问题[31]。LSTM 模型用门控机制来控制信息的更新或丢弃，引入了输入门、遗忘门、输出门，以此去除一些对当下情况不重要的内容，使得信息保存时间延长。

GRU 模型是LSTM 模型的一种变体，拥有与LSTM 模型相似的处理效果，结构更加简单，只包括2 个门[32]。具体结构如图1 所示，其中r和z分别为重置门和更新门，h和分别为当前状态的激活信息和候选激活信息。

图1 GRU模型结构Fig.1 Structure of GRU model

更新门用于控制前一时刻的状态信息带入情况。重置门决定前一状态有多少信息需要遗忘。这2 个门控向量决定了哪些信息能够作为门控循环单元的输出。

1.4 加权组合模型及其构建过程

不同的模型具有不同的特点，且对数据信息的感知程度不同，因此本文对BP，GRU 和LSTM 模型进行加权组合，以期提升预测精度，具体过程如图2。

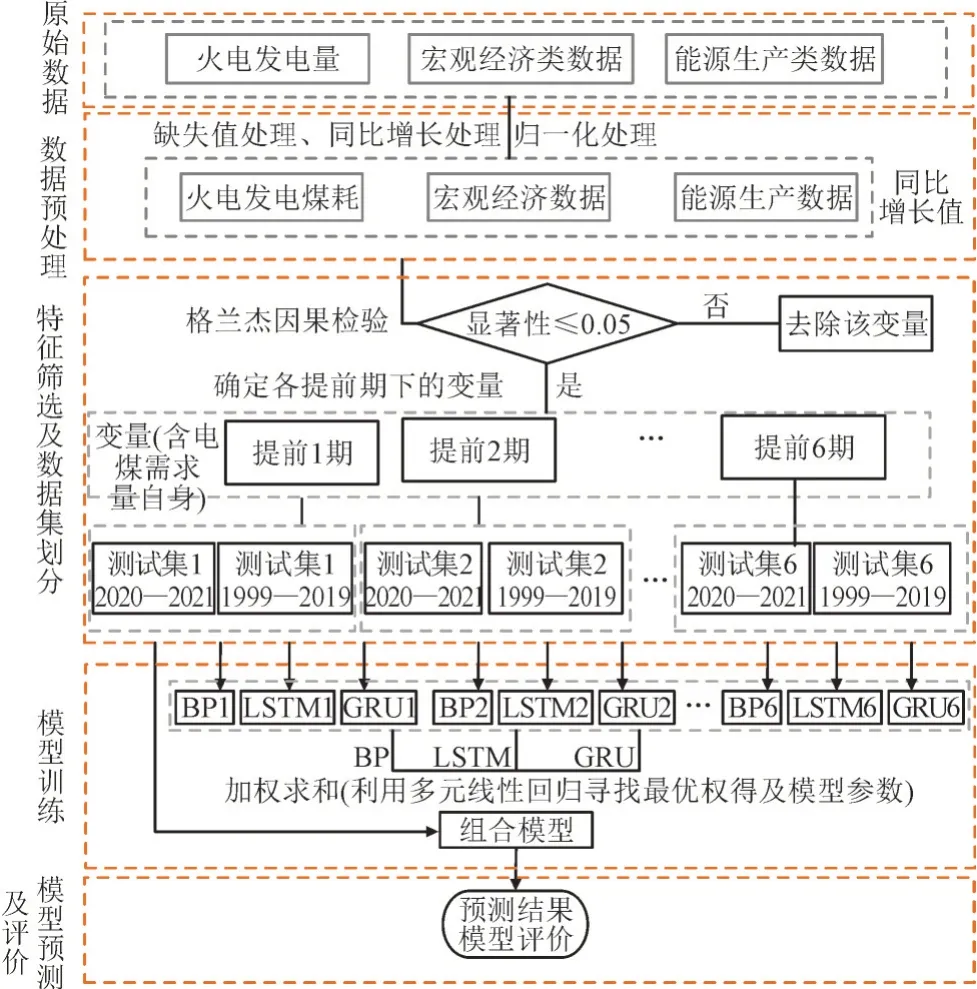
图2 建模过程Fig.2 Modeling process

1）数据预处理。收集火电发电量、宏观经济以及其他能源生产数据。采用均值插补法处理原始数据缺失值，然后计算同比增长值并做归一化处理。

2）特征筛选。对预处理后的数据进行格兰杰因果检验，筛选5%显著性水平下影响电煤需求量的因素，并确定变量影响电煤需求的提前期。

3）模型训练。

（1）子数据集构建及划分。利用筛选的提前期变量构建不同提前期范围下的子数据集，即将属于同一提前期的变量归入同一个子数据集，若设定最大提前期数为n，则会提取n个子数据集。然后对n个子数据集划分训练集和测试集。

（2）单个模型训练。利用不同的数据集分别训练BP，GRU 和LSTM 子预测模型，共得到3×n个子预测模型。

（3）组合模型构建。分别从BP，GRU 和LSTM3类子模型中各选取1 个子模型。然后，对所选的子模型进行加权组合，利用回归寻找各个子模型的最优权重及参数。最后根据最优权重和参数构建组合模型。

4）预测及评价。对比不同模型的预测结果及误差，验证组合模型的有效性。

2 实证研究

2.1 数据来源及预处理

2.1.1 数据来源

本文选取1998 年1 月至2021 年12 月共288个月的经济、能源生产等数据作为研究数据，主要包含月度火电发电量、发电标准煤耗、价格指数、工业经济增加值、社会消费品零售总额、水泥产量等共57 个变量，数据均来源于国家统计局和Wind 金融数据库。

考虑到我国月度电力燃煤需求难以获取，且火电主要来源于燃煤发电，因此将火电发电量所换算的标准煤耗近似等于电煤的标准煤耗量。每年的发电单位标准煤耗如表1 所示，由表1 可以看出不同年份的火力发电单位标准煤耗不同，由1998 年的373 g/kWh 下降至2021 年的285 g/kWh。

表1 历年火力发电单位标准煤耗表Table 1 Standard coal consumption table for power generation over the years

2.1.2 数据处理

由于变量含有时间变化趋势，某一时刻会受到前后时刻值的影响，因此本文采用均值插补法填补缺失值。各月份火电发电量及换算成标准煤耗趋势如图3 所示，由图3 可以看出火电发电量和火电换算成标煤量变化趋势一致，均呈现波动上升的趋势，存在季节性和趋势性。为消除季节和趋势因素对预测的影响，本文对每一个变量采用同比增速处理。

图3 火电发电量及火电换算成标煤量趋势Fig.3 Trend of thermal power generation and thermal power conversion into standard coal quantity

神经网络方法多采用梯度下降寻优，变量值的数量级将会影响模型寻优能力。因此，本文对数据进行归一化处理，具体计算公式如式（1）所示:

式中：x_s为归一化后的值；xmin为序列中的最小值；xmax为序列中的最大值。

经过同比增速处理及归一化之后的月度火电发电标准煤耗需求量如图4 所示，数据预处理消除了火电发电标准煤需求量的趋势性和周期性波动。

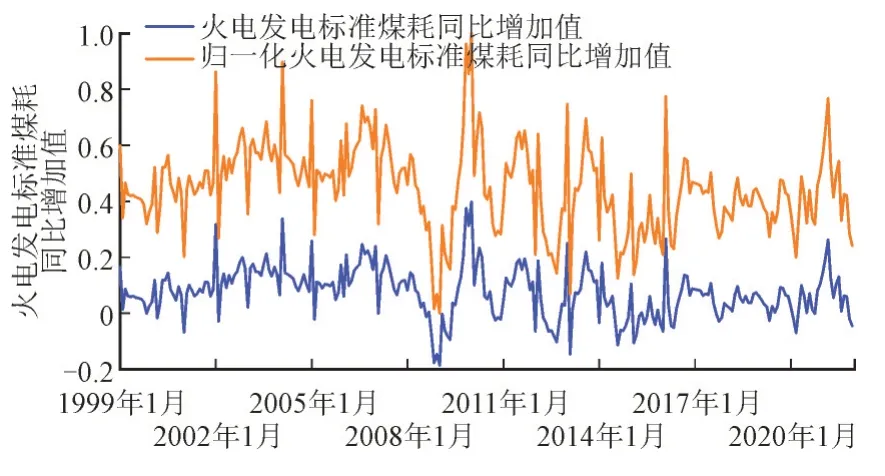
图4 预处理后的电煤需求量Fig.4 Thermal coal demand after preprocess

2.2 变量筛选

本文对数据预处理后，采用Granger 筛选5%显著性水平下影响电煤需求量的变量，结果如图5 所示。其中每个方格表示各变量（变量名分别用v1～v57 代替）分别在提前1—6 期下的格兰杰因果关系显著性水平。红色表示显著性水平在5%以下的提前期（图5 中用t-1 至t-6 表示提前1 期至提前6 期的范围）变量，显著性水平越低，红色越深。最终保留的经济和能源生产2 大类型中共26 个变量，经济方面主要有部分价格指数、进出口总值累计增长、出口总值同比增长、国家财政收入、RPI 同比值、PPI 同比值、城市CPI 同比值等；能源生产方面主要有合成橡胶产量当期值、水泥产量累计增长等。

图5 格兰杰检验结果Fig.5 Granger test results

不同经济、能源生产因素对电煤需求量存在不同期的波动传导影响，且同一变量或不同变量在不同提前期范围下对电煤需求量的影响不同，因此根据Granger 计算的结果构建不同提前期范围下数据集。本文共构建6 个子数据集，表2 展示了每个子数据集的提前期时间范围和保留的变量个数。

表2 不同提前期范围的变量个数Table 2 Number of variables in different lead time ranges

2.3 数据集划分及实验评价指标

本文将每个子数据集中1999 年1 月至2020年12 月划分为训练集，以此训练模型；2021 年1 月至2021 年12 月的数据作为测试集，用于验证模型的有效性。

为评价模型的预测性能，选择平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）和均方根误差（Root Mean Square Error，RMSE）作为预测评价指标，二者的值分别为EMAP和ERMS，值越小，说明预测值与实际值之间的误差越小，预测精度越高。

2.4 模型构建及结果分析

2.4.1 模型构建

为提升电煤需求预测精度，本文构建基于BP，LSTM 和GRU 模型的加权组合预测模型。首先用BP，LSTM，GRU 模型分别对6 个数据集进行预测，预测结果如图6 所示，各模型预测误差如表3所示。

表3 不同模型在各数据集下的误差指标值Table 3 Error index values of different models under different datasets

图6 不同模型在不同数据集中的预测结果Fig.6 Prediction results of different models under different datasets

图6 展示了不同模型基于不同数据集的预测结果。其中，黑色线表示真实值，红色、蓝色、绿色线、分别表示BP 模型，GRU 模型，LSTM 模型预测结果。从图6 中可以看出，不同模型基于不同数据集预测效果不同。综合来看，GRU 模型预测值与真实值关系较为稳定，LSTM 模型在部分数据集中预测值与真实值更接近，与表3 结论相一致。

从表3 可以看出，EMAP和ERMS最小时BP 模型对应的数据集为子数据集2，GRU 模型对应的数据集为子数据集1，LSTM 模型对应的数据集为子数据集5。其中，基于子数据集5 训练的LSTM 模型精度最高，验证了LSTM 模型可以较好感知多变量关系及时序信息。从预测稳定性来看，BP 模型最稳定，其次是LSTM 模型，最后是GRU 模型。

为提升预测精度，本文构建组合模型预测电煤需求。分别从3 种单一模型中选择1 个模型进行多元回归加权组合，并利用组合模型进行预测。组合模型参数如表4 所示，模型如式（2）所示。

表4 模型参数表Table 4 Model parameter table

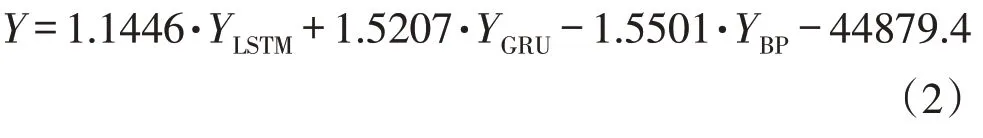
式中：Y为组合模型预测值；YLSTM为LSTM 模型预测值；YGRU为GRU 模型预测值；YBP为BP 模型预测值。

2.4.2 不同模型对比

依据各模型基于不同提前期数据集下的预测评价指标，BP，LSTM 和GRU 模型分别在子数据集2、子数据集5、子数据集1 数据集下预测效果最好。为验证组合模型的预测效果，将最佳提前期下的各单一模型与组合模型进行对比，如图7 所示。

从图7（a）可知，相较于单一模型，组合预测模型对真实值的拟合效果更好，其预测效果优于单一模型，能够较好地感知电煤需求的变化趋势与极值。

从图7（b）可知，组合模型的箱体最窄、均值线最低且接近0，其次是BP 模型，然后是GRU 模型，最后是LSTM 模型。同时，组合模型的样本点百分比误差的集中度更高，说明组合模型的预测性能最好且最稳定，单一模型的预测精度较差且不稳定。为进一步评价组合模型和单一模型的预测性能，分别计算了单一模型和组合模型的EMAP和ERMS，如表5 所示。

从表5 可知，组合模型的EMAP和ERMS值最小。相比于单一模型，精度提高约3 个百分点，说明基于BP 模型、LSTM 模型和GRU 模型的加权组合电煤需求预测模型预测效果最好，性能最稳定，可以有效提取影响电煤需求的多个因素及时序信息和规律。因此，组合预测模型可以综合利用单个模型的优点，弥补单一模型存在的不足，提升预测精度。

3 结语

电煤需求随时间动态变化，受多种因素影响。本文利用Granger 筛选其影响因素，构建基于BP，LSTM 和GRU 的加权组合模型预测我国电煤月度需求。算例表明，相较于单一模型，组合预测模型性能更好，提升了电煤需求预测精度，提高了双碳目标下保障电力系统稳定运行和能源供给安全的能力。

然而，本文工作还需优化，如变量筛选和模型构建。变量筛选及提前期确定方面，Granger 主要采用了受约束回归模型，易受其它因素影响，鲁棒性不足，且精确度有待提升。未来可进一步优化格兰杰因果模型，提升变量筛选及提前期确定的准确度。同时，现有模型仅考虑了BP，LSTM 和GRU，未来可引入其他时序模型、树模型等，以提升预测精度。