考拉兹猜想

陈新龙

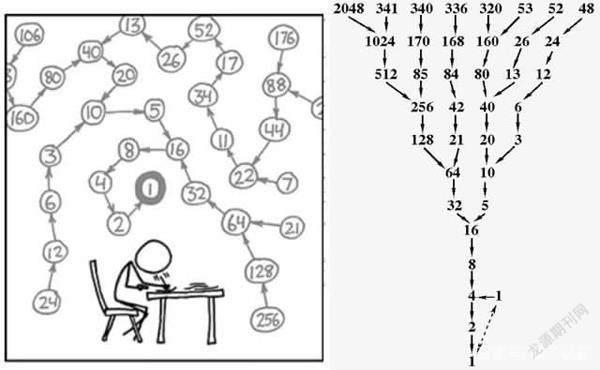
考拉兹猜想是德国的数学家洛萨·考拉兹在1937年提出的一个著名的猜想，任意正整数n，如果n是偶数，就将它减半（即n/2）;如果它是奇数，则将它乘3加1（即3n+1），不断重复这样的运算，经过有限步骤后，一定可以得到数字1。假设我们设置初始数字为3，按照上述变换的规则，可以得到一个数列3，10，5，16，8，4，2，1。

这个猜想看似相当简单，但实际上却很难证明，80多年来，众多的数学家始终未能解决它，只能说从已有的测试中还没有找到反例。今天我们通过Scratch中的自定义模块结合递归的思想，来模拟一下该数学猜想。

首先复习一下什么是递归：简单来说递归就是程序调用自身。递归的思想就是把一个复杂问题层层转化为多个规模更小的问题，原问题被拆解成子问题后，递归调用繼续进行，直到子问题不需进一步递归就可以解决的地步为止。要注意递归必须有一个明确的结束条件，称为递归出口。

就拿考拉兹猜想为例，如果输入的数字是10，则10除以2得5，这时我们需要来判断5，这一步就是递归。接下来5乘以3再加1得16，我们又需要判断16，这步也是递归。直至最后数字的结果为1时，递归结束，程序也结束。

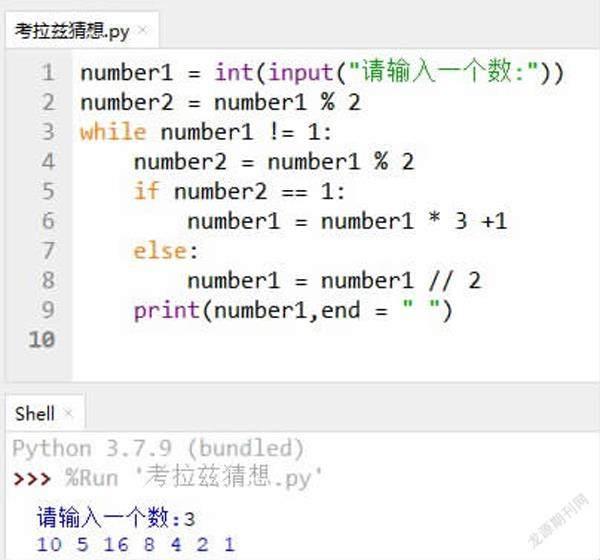
理解递归思想后，开始编写代码，按照题目分析首先将问题拆分成两大部分，当最终结果数字n的值等于1的时候结束循环，程序终止。当结果不等于1的时候，继续拆分成两部分，判断数字n的结果是奇数还是偶数，如果是偶数的话，在原基础上将数字整除2，然后将数字插入到列表中，如果数字是奇数的话，在原基础上将数字乘3加1，然后将数字插入到列表中。最后将每次执行完的结果输出。

你也可以尝试用Python来编写考拉兹猜想，也欢迎大家分享更多的不同的思路。