人工水下沙坝研究进展

潘 毅，薛仕磊，王雪迎，匡翠萍，陈永平，张长宽

（1. 河海大学港口海岸与近海工程学院，江苏 南京 210024；2. 同济大学土木工程学院，上海 200092；3. 秦皇岛市海岸带生态修复工程技术研究中心，河北 秦皇岛 066001）

人工水下沙坝（submerged berm）也称近岸补沙（shoreface nourishment），指通过人工方式在近岸堆填沙坝（垂直岸线方向的宽度通常大于天然沙坝，在100～300m的范围），以起到削减波浪和给海滩缓慢供沙的效果，是一种间接的养滩方式。相比常规的人工养滩，人工水下沙坝对海滩的影响是间接的，且具时间滞后性，但因其环境扰动小、造价相对较低（省去了海滩整平环节，且有时客沙来自附近港口的疏浚），在沙质海岸修复中有其独特优势。人工水下沙坝的应用最早可追溯到1935 年美国圣塔芭芭拉的海滩修复工程［1-2］，其后在世界范围内的养滩工程中得到了广泛应用［3-4］；我国的人工养滩起步较晚，人工水下沙坝的应用始于2008 年的北戴河中直浴场应急治理工程［5］，但在后续一系列养滩工程中得到了较多应用，如北戴河西海滩养护工程［6］、老虎石公园养滩工程［7］、新开河口至南山段养滩工程［8］等。

近年来，随着气候变化引起全球范围内海岸防灾压力的提升，兼具有效性、可持续性和性价比的海岸软防护在世界范围内得到广泛重视［9］，世界各国均提出了一些海岸软防护相关的国家战略，我国的生态海堤建设、蓝色海湾整治行动、海岸带生态保护和修复等亦属此类。在此背景下，人工水下沙坝在未来海岸防护中有更为广泛的应用空间，给相关科学研究提出了更高的要求。

人工水下沙坝与波浪之间的相互作用是其工程应用相关的重要科学问题，该问题又可以分为2 个方面，波浪作用下人工水下沙坝的迁移演变和人工水下沙坝对波浪的消减效应。上述问题会受到动力条件、岸滩地貌、泥沙粒径、人工沙坝自身尺度等众多因素的影响，在工程应用中，需要结合工程目的对上述因素进行综合考虑来合理设计养滩方案。人工水下沙坝的研究方法包括现场观测、物理试验和数值模拟；现场观测提供第一手的规律性认知，物理试验和数值模拟能够针对特定问题开展研究，但又各有偏重和局限性。本文首先综述了人工水下沙坝与波浪相互作用的最新研究进展，然后分别从经典案例和核心思想的角度论述了物理试验和数值模拟研究方法，最后结合现有成果，提出了人工水下沙坝工程应用上的建议以及未来的研究展望，以期为海岸防护工程和相关科学研究提供参考依据。

1 人工水下沙坝与波浪的相互作用

人工水下沙坝对海滩的作用包括缓慢补沙、削减波浪，或二者兼而有之［10］。二者对应的科学问题分别为人工水下沙坝与波浪的相互作用的2 个方面，即波浪作用下人工水下沙坝的迁移演变和人工水下沙坝对波浪的消减效应，本节对这两方面的最新研究进展进行综述。

1.1 波浪作用下人工水下沙坝的迁移演变

对岸滩进行持续、缓慢的补沙是人工水下沙坝的重要功能。因此从迁移演变的角度上来讲，人们更为关心人工水下沙坝泥沙的向岸—离岸迁移，波浪作用下的向岸—离岸输沙可以视为人工水下沙坝演变的主要动力机制。波浪作用下的向岸—离岸输沙受诸多因素的影响，如水深、海滩坡度、泥沙粒径、渗流、波浪不对称性等，以及近几年关注较多的波浪引起水质点运动的速度偏度和加速度偏度等。总体来说，受波浪浅水变形引起的一系列效应影响，近岸泥沙在常浪条件下存在一个向岸输沙的长期趋势，这也构成了人工水下沙坝能够发挥补沙效应的理论依据。但向岸输沙会受到各种因素的影响，其出现并不是必然的，而且在大浪条件下会形成数倍甚至数10倍于常浪条件下的离岸输沙，可能导致人工水下沙坝的迅速耗散。因此需要对人工水下沙坝予以科学布设以使其发挥理想的补沙效应。波浪作用下的向岸—离岸输沙是一个综合性的课题，本文不再予以详述，而是针对人工水下沙坝本身演变相关的研究进展开展综述。首先介绍用于表征人工水下沙坝迁移演变的主要参数，然后阐述对人工水下沙坝迁移演变规律的最新认知。

1.1.1 迁移方向和工程寿命

人工水下沙坝的迁移演变可以用迁移方向和工程寿命等参数来表征。迁移方向关系到人工水下沙坝最终能否对海滩形成有效养护，是人工水下沙坝最重要的、研究最早的特征参数。早期研究通过一些量纲为一参数来判断天然沙坝和人工水下沙坝的迁移方向［11-12］，这些研究大多基于长期现场观测数据。Larson 和Kraus［13］总结了基于量纲为一参数的判断指标，提出了如下3个判定指标的临界条件：

式中：H0为深水波高；L0为深水波长；T为波浪周期；ω为泥沙沉速；D50为泥沙中值粒径；g为重力加速度。式（1）—（3）可用于天然沙坝和人工水下沙坝迁移方向的判断。在进行迁移方向判断时，首先绘制上述公式对应的曲线，然后针对具体案例计算公式两边的量纲为一参数，与曲线点绘于同一坐标系；如果该点落在式（1）和式（2）曲线左侧或式（3）曲线右侧，则表示沙坝向岸迁移，反之则向海迁移。量纲为一参数判断指标在判断人工水下沙坝的迁移方向时有较好表现，如Hands［14］用量纲为一参数对11 个人工水下沙坝的迁移方向进行了判断，判断结果均与现场数据一致。

仅靠迁移方向不能完全表征人工水下沙坝的迁移特征，还需对人工水下沙坝迁移演变的时间特征予以有效表征。近期研究中，人工水下沙坝工程寿命（lifetime）的概念得到了较多应用［15］。人工水下沙坝可以视作对沙质海岸中天然沙坝周期性演变的一个人为扰动，大量现场观测表明，该扰动多数情况下会完全打乱原有天然沙坝的演变规律，在一段持续大约1～7 年的扰动期过后，原有的天然沙坝周期性演变过程会逐渐恢复［16-17］，这个扰动期称为人工水下沙坝的工程寿命。工程寿命受到众多因素的影响，据Gijsman 等［4］基于21 个人工水下沙坝案例的现场研究得知，人工水下沙坝的断面面积和布设水深对工程寿命为正影响，且前者影响大于后者；天然沙坝的演变循环周期和天然沙坝的断面面积对工程寿命为负影响，且前者影响大于后者。据另外一些案例研究，使用较大粒径的客沙能够显著增加人工水下沙坝的工程寿命［18］。Gijsman 等［4］也提出了相对工程寿命的概念，即将人工水下沙坝的工程寿命与天然沙坝的演变循环周期做比值，用来除去天然沙坝本身的演变特征对工程寿命的影响。总体来说，人工水下沙坝的工程寿命影响因素众多，目前没有通用性的判定标准；对具体案例的工程寿命预估则需要借助物理试验或数值模拟的手段。

1.1.2 迁移演变规律

总体上，人工水下沙坝的泥沙输运规律和天然沙坝类似，常浪条件下形成向岸输运，而大浪条件下则形成离岸输运和总量耗散。在常浪条件下，人工水下沙坝的向岸迁移速率很大程度上受水深控制［19］，将人工水下沙坝布设在更浅的水深处能显著提高其向岸迁移速度；在大风浪过程中，风暴潮的峰值阶段会形成强烈的离岸输沙，而风暴潮的初始和消散阶段则会出现弱的向岸输沙［20］。

从整个工程寿命期间的迁移演变过程来看，人工水下沙坝对当地地貌过程的最显著影响是完全打乱了原有天然沙坝的演变规律［4］，如改变天然沙坝的迁移方向、迁移范围等。就其自身演变特征而言，在工程寿命的初期和中期，人工水下沙坝的迁移和消散速率通常较为缓慢；而在工程寿命的末期，人工水下沙坝会迅速消散［16-17］。值得注意的是，在低能沙质海岸（低能沙质海岸是指波浪能较小、潮差较小的沙质海岸；Jackson等［21］对低能沙质海岸提出了一个基于有效波高以及滩面（前滨）宽度的建议性判断标准，而后期的研究中常把总体波能较小的沙质海岸归于此类［3，22］）中，人工水下沙坝表现出不同于常规沙质海岸中的演变特征。现场观测表明，低能沙质海岸中的人工水下沙坝总体上位置移动非常小，取而代之的是发生剖面的非对称变形，向海坡逐渐变缓，向岸坡坡度变化不大，整体呈现向海坡被“拉长”、坝顶位置向岸移动的特征。这种现象在美国佛罗里达的迈尔斯堡海滩［3］和我国的北戴河海滩［22-23］均有报道。图1 给出了位于我国北戴河的2 个低能沙质海岸中人工水下沙坝演变的典型案例。Pan等［22］指出，在低能沙质海岸中，人工水下沙坝演变和原有海滩剖面的演变相对独立，可以分别根据平衡剖面理论进行推导，给出了适用于低能沙质海岸的、含人工水下沙坝的平衡剖面形式。该平衡剖面包含背景剖面和人工水下沙坝剖面两部分，背景剖面和人工水下沙坝向海坡用考虑沿剖面泥沙粒径差异的改进的平衡剖面公式［24］来计算，见式（4）；而人工水下沙坝向岸坡坡度则简单地取一个经验值，如4%。

图1 低能沙质海岸中人工水下沙坝演变典型案例（数据来源于北戴河海滩）Fig.1 Typical cases of evolution of submerged berms in low energy sandy beaches (data from a beach in Beidaihe,China)

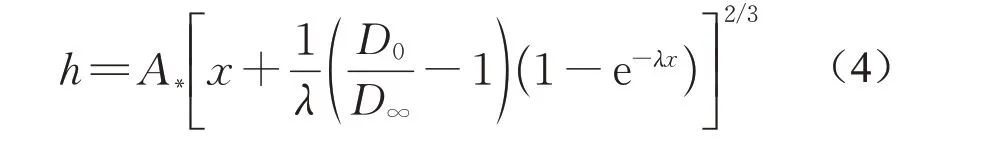
式中：x为剖面上任一点距岸线的距离；h为x处的水深；D0为岸线处单位水体的等效能量耗散；D∞为深水处单位水体的等效能量耗散；λ为表征D0向D∞变化速率的参数。

此外，因为低能沙质海岸中天然沙坝几乎不存在周期性演变，故低能沙质海岸中人工水下沙坝的工程寿命不再适合以上文提到的“扰动期”来计算，笔者认为其工程寿命可以以其彻底消散或消散到原有体积的某个百分比来定义，具体还需未来研究进行进一步探讨。

1.2 人工水下沙坝的消波效应

人工水下沙坝的波浪透射系数是表征其消浪作用的重要表征参数。波浪透射系数的概念来自离岸潜堤，指透射波高和入射波高之间的比值，其数值大小影响人工水下沙坝/离岸潜堤后方的岸滩演变特征；但人工水下沙坝的剖面形状无法像离岸潜堤一样以坝高、坝宽等参数来表征，故现有研究多为针对特定案例的案例研究或规律性研究，鲜有人工水下沙坝波浪透射系数的经验公式。

人工水下沙坝消波效应的研究多基于物理试验。早期研究者多针对人工水下沙坝的初始断面（规则断面）开展透射系数的试验研究，如Zwamborn等［25］针对南非德班湾海滩人工水下沙坝工程开展断面演变动床试验的同时，也开展了一系列定床试验，研究了不同坝顶宽度和入射波高情况下透射波高和入射波高之间的关系，这些经验关系以图表的方式给出；也有学者通过理论推导来研究梯形断面人工水下沙坝的波浪透射系数，如赵多苍等［26］将人工水下沙坝概化为单一坡度海床上的梯形断面，推导得到了人工水下沙坝坝顶的沿程波高变化公式，并通过物理试验对公式进行了验证，结果表明，当沙坝所在位置水深较小时该公式表现较好。但Zwamborn等［25］和赵多苍等［26］的研究仅针对梯形断面开展，未能给出不规则断面形状人工水下沙坝的波浪透射系数计算方式。近期，一些案例研究针对特定的人工水下沙坝工程，参照相对坝高、相对坝顶水深等量纲为一参数，通过水槽试验研究人工水下沙坝演变过程中透射系数的变化过程［27-28］，试验结果表明透射系数与上述量纲为一参数之间存在较好相关性，并提供了相关图表可供设计参考。上述研究将研究对象从规则断面推进到不规则断面，并参照一系列量纲为一参数进行了规律性探讨，但仍未给出定量的计算公式，其原因在于不规则的断面型式难以合理表征。因此，如何概化人工水下沙坝的剖面形状并提出量化的波浪透射系数公式成为该方向研究需要解决的关键问题。

2 研究方法

由第1 节论述可知，对于人工水下沙坝的迁移演变过程和消波作用尚无通用性的定量预估方法；因此，设计具体工程案例时仍需借助物理试验或数值模拟的手段。总体来说，物理试验侧重研究人工水下沙坝的基本演变规律、风暴短期侵蚀和波浪透射系数，数值模拟侧重研究人工水下沙坝的中长期演变规律。从2 种方法的特点来讲，涉及泥沙的物理试验没有统一的设计准则，尤其是泥沙比尺需要针对具体问题进行讨论；而数值研究方法相对来讲则具有通用性，数年来在众多学者的研究中逐步完善。因此，本节对物理试验采用案例的方式进行论述，以期为相关研究提供借鉴；对数值研究方法则直接阐述研究方法的发展历程及核心原理，为相关研究提供直接参考。

2.1 物理模型试验研究

人工水下沙坝的物理试验研究通常采用波浪动床试验针对具体工况开展，试验设计的核心问题为泥沙粒径和比重比尺，需要针对具体案例对不同相似率进行合理取舍。这里着重论述经典物理试验的研究背景、比尺设计原则和主要结论。

多数人工水下沙坝演变相关的物理试验研究都是针对大浪过程开展的。最早探讨人工水下沙坝演变特征的物理试验研究可以追溯到1970 年，Zwamborn 等［25］以南非德班湾海滩人工水下沙坝工程为原型开展了水槽试验，目的在于研究水下沙坝的基本侵淤特征；该试验的比尺基于弗劳德准则和剪切—沉降相似准则进行设计（剪切—沉降相似准则指剪切流速和泥沙沉速比值的相似）；基于试验结果，Zwamborn等［25］提出了一个以深水波陡和量纲为一参数（gH0）0.5ω-1来判断人工水下沙坝侵淤的经验关系。Grasso等［20］在水槽中采用塑料模型砂开展了风暴过程的人工水下沙坝演变试验研究，目的在于探究一场风暴过程中人工水下沙坝的演变特征；该试验研究通过控制模型砂粒径和密度，使模型的弗劳德数、希尔兹数和劳斯数与原型相同；Grasso等［20］的试验结果表明，风暴潮的峰值阶段会形成强烈的离岸输沙，而初始和消散阶段则存在弱的向岸输沙，这一结果与现场观测结果能够相互印证［29］。Smith等［30-31］在港池中开展了人工水下沙坝在侵蚀性高能波浪（原型有效波高3.6 m，谱峰周期6.7 s，TMA谱）作用下的演变试验，且考虑沿岸流的影响，试验比尺根据弗劳德准则和相对沉速相似［32］进行设计；由于波能过大，Smith等试验中的人工水下沙坝迅速消散，泥沙在沿岸流的作用下向下游（即沿岸流流向方向）沿岸输运，人工水下沙坝仅起到消浪作用，而未发挥养护效应。也有一些研究针对具体工程案例开展，为工程的设计和优化提供参考依据。如赵多苍等［33］针对北戴河具体工程案例开展了二维和三维的物理试验研究，泥沙粒径比尺采用起动波高相似来计算，依据试验结果对各种水动力参数对沙坝稳定性的影响进行了探讨，并指出在大浪下人工水下沙坝坝顶由于波浪破碎会形成明显的侵蚀沙槽；拾兵等［34］对水位变化对该侵蚀沙槽的影响进行了进一步探讨，指出沙槽的深度和范围随水位和波高的增加而增大，位置随水位的增加而向岸移动。

总体来说，目前风暴大浪条件下的人工水下沙坝演变试验都表现出明显的离岸输沙和侵蚀性，但缺少低波浪能条件下的波浪动床试验研究。Smith等［31］总结指出，需要开展低波浪能条件下的波浪动床试验研究，以掌握低波浪能条件下人工水下沙坝演变的基本特征，并为数值模拟提供必要的验证数据。近期，Pan等［35］开展了一系列低波浪能条件下的人工水下沙坝演变试验，该试验的泥沙粒径比尺和重度比尺采用“局部拟合法”［36］根据弗劳德准则、沉速相似和起动相似设计，探讨了低波浪能条件下波浪参数对人工水下沙坝演变趋势的影响，试验结果表明低波浪能条件下水深和波浪引起的水质点速度偏度是影响人工水下沙坝演变的主控因素。

2.2 数值研究方法

与物理试验相比，数值模型的优势之一是能够开展长时间尺度的模拟，使复演和预测人工水下沙坝的中长期（工程时间尺度）演变成为可能。事实上，数值模型在人工水下沙坝的短期（风暴期间）演变方面也取得了较多进展，如XBEACH模型［37］在沙质海岸大浪侵蚀过程的模拟中有较好表现，但短期演变数值模拟不作为本文的论述重点。本文着重针对适用于人工水下沙坝中长期演变的“基于过程的剖面演变模型”的发展历程和核心原理开展论述。

基于过程的剖面演变模型根据向岸—离岸输沙来计算剖面内的泥沙输运，在考虑沿岸输沙分量之后能够较好地复演近岸的岸滩变化过程［38］。值得注意的是，这里所谓“基于过程的”并非采用相位解析波浪模型直接模拟波浪与泥沙的相互作用过程，而是采用相位平均的波浪模型来驱动，但考虑各种动力环境参数（如坡度、平均流、水质点速度偏度、加速度偏度等）对一个波周期内输沙过程的影响，所有动力环境参数的贡献叠加后得到最终的输沙率，这种实现方式使得中长时间尺度岸滩演变的数值模拟成为可能。在具体实现方式上，这类模型通常求解波能守恒或波作用量守恒方程，并考虑水滚能的沿程发生和耗散，求解沿程波浪能和水滚能；波浪能用于计算波浪引起的水质点速度，水滚能则用于计算水体紊动强度，进而计算流速剖面；波浪引起的水质点速度和流速剖面则一起用于计算各种动力环境引起的输沙率。

沙质海岸的剖面演变模型最早可以追溯到SBEACH 模 型［39］和 UNIBES-TC 模 型［40］。SBEACH 模型的向岸—离岸输沙率基于单位水体的能量耗散来计算，尚称不上“基于过程的”剖面演变模型，但其模型架构为后期的模型发展奠定了基础；UNIBES-TC 模型最早由Roelvink 和Stive［40］开发，并在使用中进行了持续维护和改进，在世界各地的人工水下沙坝研究中得到应用［17，41］。在众多学者的贡献下，各种近岸动力环境要素对输沙的影响被纳入剖面演变模型，如Douglass［42］引入了浅水波引起的速度不对称性对剖面输沙的贡献，Spielmann等［43］引入了水滚过程的影响，Ruessink 等［44］提出了适用于相位平均模型的速度偏度和加速偏度的计算方法，Wlastra 等［45］则把沿岸流对向岸—离岸输沙的影响考虑在内。随着对各类近岸过程的综合考虑，该类模型开始被称作“基于过程的剖面演变模型”。近年来，Dubarbier等［38］集成了相关成果，并将模型从一维拓展到二维，波浪参数和水流参数分别采用波作用量守恒方程和浅水方程计算，输沙采用式（5）-（7）计算：

式中：Qc、Qw和Qg分别为平均流、波浪和底坡引起的泥沙输运；Cc、Cw和Cg分别为平均流、波浪和底坡相关的输沙系数；U为总流，包括平均流以及波浪引起的水质点振荡流速；i和j分别指代向岸—离岸和沿岸方向；-ui和-uj分别为平均流在向岸—离岸和沿岸方向的分量大小；u͂为波浪引起的水质点振荡流速；k为波数矢量，其数值为波数，方向为波浪传播方向；ki和kj分别为k在向岸—离岸和沿岸方向的分量大小；φ为泥沙内摩擦角；ws为泥沙沉速；Z为剖面高程；κb和κs分别为底沙和悬沙输运相关的参数；εs为悬沙输运相关的数值参数，取0.015。更多参数相关的具体计算方式参看文献［38］。通过上述计算方式，Dubarbier等［38］的模型实现了从耗散型到反射型海滩转变过程中6 种海滩状态全过程的复演，标志着基于过程的剖面演变模型对近岸岸滩演变的模拟获得了较高的可信度；但该模型中存在一些输沙相关的经验系数，需要现场资料对其进行率定，因此，降低经验参数对模拟结果的影响也成为了该类模型今后需解决的问题。

3 工程应用上的建议

在人工水下沙坝的构筑长度方面，van Leeuwen等［46］基于数值试验指出，人工水下沙坝在沿岸方向长度的增加能显著提高其工程寿命；然而Brutsché等［3］指出，在低能沙质海岸中构筑人工水下沙坝时应考虑间断式的坝身，以增加近岸的水体交换，防止水质恶化；我国黄渤海沿岸的很多低能海滩修复即使用了间断式的人工水下沙坝布置方式［47］。事实上，上述2 个观点并无矛盾，通常当近岸波能较大时，人工水下沙坝的工程寿命是工程设计时考虑的重要参数；而对于低能沙质海岸，人工水下沙坝的消散较为缓慢，而其后方的水体则由于波能较低而流动性弱，使得其后方水质成为需要考虑的因素之一。

在人工水下沙坝的布设位置方面，当海滩剖面存在一条天然沙坝时，为了节省成本，人工水下沙坝常选择在原有的天然沙坝上加宽加高，如我国北戴河西海滩的人工水下沙坝［22］。当原有海滩断面存在多条天然沙坝时，Spielmann等［43］基于数值试验结果指出，在原有外层沙坝的基础上构建人工水下沙坝是更优的选择，能够更有效地削减波浪和保护内层沙坝；事实上，很多工程案例中的人工水下沙坝布设位置也是据此选择的，依托外层天然沙坝的内侧［16］或外侧［17-18］来构筑。

在进行人工水下沙坝的工程寿命设计时，需要依据工程目的对其离岸距离（布设水深）和客砂粒径进行合理选择。总体上说，离岸距离越近（布设水深越浅），人工水下沙坝的移动性越强［19］，更有可能形成显著的向岸输沙，发挥养护效应；然而，移动性越强的人工水下沙坝也越容易在大浪引起的离岸输沙和沿岸输沙作用下快速消散［30-31］，引起工程寿命的降低。客砂粒径也存在类似的效应：客砂粒径越大，人工水下沙坝就越稳定［18］；但人工水下沙坝稳定性的增加也意味着人工水下沙坝将会更多地发挥消浪效应，而非更为直接的养护效应。综上，应考虑工程目的（养护效应或消浪效应）以及当地的水动力条件，对人工水下沙坝离岸距离（布设水深）和客砂粒径进行合理设计。

4 结语

对人工水下沙坝的研究进展进行了综述，主要内容包括人工水下沙坝与波浪的相互作用的最新研究进展、主要研究方法、工程应用上的建议和未来的研究展望。

人工水下沙坝与波浪之间的相互作用可以分为2个方面，即波浪作用下人工水下沙坝的迁移演变和人工水下沙坝对波浪的消减效应。波浪作用下人工水下沙坝的迁移演变是人工水下沙坝的研究重点，其迁移方向可以根据一系列量纲为一参数进行判断；工程寿命用于表征人工水下沙坝对天然海滩周期性演变的扰动时间，现有研究对工程寿命及工程寿命期间的演变特征有一定的定性认知，但做不到定量预测。人工水下沙坝对波浪的消减效应与离岸潜堤类似，但因其断面形状难以表征，目前停留在案例研究和规律性认知阶段。在研究方法方面，物理试验侧重研究人工水下沙坝的基本演变规律、风暴短期侵蚀和波浪透射系数，数值模拟侧重研究人工水下沙坝的中长期演变规律；本文对相关物理试验和数值研究方法进行了简述。最后，从构筑长度、布设位置和工程寿命设计的角度提出了人工水下沙坝工程应用上的建议。

在对研究进展进行论述的过程中提出了未来研究展望，可以总结为：在迁移演变机制方面，人工水下沙坝与天然海滩地貌过程的相互影响机制需要进一步揭示；在消波效应方面，适用于不规则断面的波浪透射系数计算公式有待提出；在数值研究工具方面，基于过程的剖面演变模型对经验参数和现场数据的依赖性需要进一步降低。

作者贡献声明：

潘 毅：提出选题，论文框架设计，论文写作与修改。

薛仕磊：数据整理，论文写作。

王雪迎：查阅资料，图表绘制，论文写作。

匡翠萍：工程案例分析，论文写作与修改。

陈永平：学术指导，论文写作。

张长宽：论文框架设计，论文审阅。