负弯矩作用下钢-CLT组合梁-钢柱组合节点转动性能有限元模拟*

凌志彬 穆泉蒙

（苏州科技大学土木工程学院，江苏 苏州 215011）

近年来，随着国内建筑产业的转型升级，实木类建筑材料以其具有可再生、强重比高、美观、抗震性能好、保温隔热性能好等优点，日益受到关注。从建筑全生命周期角度分析，木材具有显著的低碳优势[1]。正交胶合木（Cross-Laminated Timber，CLT）是目前研究和应用领域最为流行的实木类建筑材料，由规格材垂直交叉组坯并施胶压制而成。层板正交布置使得CLT具有良好的尺寸稳定性和近似各向同性的力学性能，可用作建筑结构中的楼板或墙体[2-4]，亦可用于桥梁结构的桥面板。钢结构具有轻质高强、抗震性能好、快速施工等优点，将CLT板与钢框架进行组合，不仅可发挥钢、木各自的材料优势，而且能充实我国建筑材料，可作为装配式建筑结构材，具有拆卸回收便捷、绿色轻质、抗震性能较好等优点。

近年来，业界对SCLTC组合节点（钢-CLT组合梁-钢柱组合节点）进行了试验和模拟研究。Nouri等[5-9]对梁柱采用腹板双角钢和剪切板连接的SCLTC组合节点进行了负弯矩试验，研究包括CLT板拼接构造和腹板角钢、剪切板的尺寸等参数变化，提出了CLT板内植筋的新型连接方式。此外，基于试验数据，通过组件法和有限元模拟对节点进行了承载力计算和参数化分析。Keipour等[10-12]对梁柱齐平端板和外伸端板连接的SCLTC组合节点进行了负弯矩试验，研究了CLT板间拼接构造如钢板连接、CLT板搭接、胶接等连接方式对节点的影响，指出CLT板拼接构造对组合节点的刚度影响很大，SCLTC组合节点与纯钢梁柱节点相比，强度提高了约81%。但是对齐平端板连接方式的SCLTC组合节点研究还不够全面，尤其是负弯矩作用下的节点转动性能，缺乏系统的理论研究。鉴于此，本文基于ABAQUS对负弯矩作用下的SCLTC组合节点的转动性能进行有限元数值模拟，重点分析该组合节点不同参数下的弯矩-转角行为、极限弯矩及初始刚度等，并研究几种影响组合节点负弯矩作用下力学性能的参数（CLT板厚度和宽度、CLT板拼接构造及楼板-钢梁连接构造）。本文通过数值拟合确定三参数模型的形状系数的建议值，得到SCLTC组合节点的弯矩-转角曲线模型，为钢框架-CLT楼板组合结构体系的试验和应用提供理论指导。

1 有限元计算模型

1.1 模型建立

采用ABAQUS建立SCLTC组合节点有限元模型。模型中CLT板与钢梁之间采用M16L100（直径16 mm、长100 mm）自攻螺钉连接，钢梁与钢柱采用齐平端板连接，钢柱附近CLT板采用8 mm钢夹板进行拼接。H型钢和钢夹板均为Q345钢材，梁、柱连接螺栓选用10.8级M20高强螺栓，CLT板拼接选用8.8级M16高强螺栓，所选用自攻螺钉为4.6级外六角自攻木螺钉。梁柱均为热轧H型钢，截面型号分别为HW250 mm× 250 mm×9 mm×14 mm、HN300 mm× 150 mm× 6.5 mm× 9 mm，柱长800 mm，梁长1 400 mm。CLT楼板由3层35 mm厚的云杉木层板制作而成。节点形式与具体尺寸如图1所示。

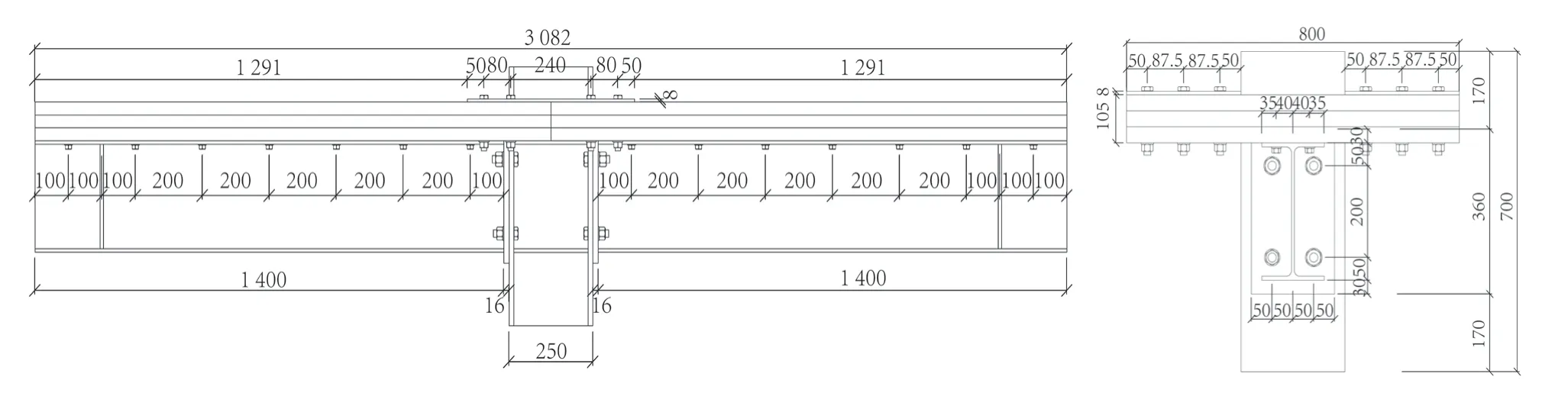
图1 SCLTC组合节点构造示意Fig.1 Schematic of SCLTC composite joints

建模过程中，做了如下假定：

1）将CLT视为无生长缺陷的均质材料，且不考虑CLT层板胶缝及层板间隙；

2）将自攻螺钉、螺栓杆简化为等效直径的光圆螺杆，即不考虑表面螺纹状况；另外，螺帽与螺栓杆视为一个整体部件，忽略两者之间的相对滑移。

1.2 材料参数

按木材纹路方向设置局部坐标系对CLT进行分层指派材料属性。本文参考已有研究[13]，对CLT材料性能进行定义，即将CLT层板视为均质的各向异性材料，云杉木弹性性能参数如表1所示，其在不同方向上的强度值和断裂能Gƒ如表2所示。

表1 云杉木弹性性能参数[13]Tab.1 Elastic properties of Spruce wood[13]

表2 云杉木在不同方向上强度值和断裂能[13]Tab.2 Strength values and fracture energy of Spruce wood in different directions[13]

钢材的应力-应变关系采用双折线强化模型描述，强化段斜率取0.01Es，泊松比μ=0.3，分析采用Mises屈服准则。

1.3 相互作用及网格划分

模型部件包括钢梁、钢柱、CLT板、钢板、螺栓和螺钉，各部件相互作用均采用表面与表面接触定义，其中法向作用采用“硬接触”，切向作用采用库伦摩擦。钢材之间的摩擦系数为0.4，钢材和CLT板的摩擦系数为0.3[7]，螺钉和CLT的摩擦系数为0.7[14]。

采用六面体实体单元进行网格划分，单元类型为C3D8R单元。为了较准确地模拟SCLTC组合节点的力学性能，对模型构件的连接处，如钢梁、螺栓、端板以及连接钢板进行了网格细化，如图2所示。

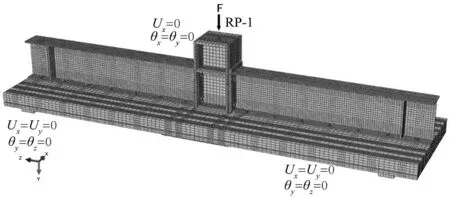
图2 网格划分与边界条件Fig.2 Meshing of specimens and boundary conditions

1.4 边界条件和加载制度

通过设置4个分析步来模拟试件的边界条件和加载制度。本模型参考试验[10]实况将试件倒置进行加载，在CLT板底创建刚体垫块来模拟支座，并在垫块底部中线施加x和y方向的位移约束和绕y和z轴的转动约束；将柱的顶部通过耦合点RP-1施加x方向的位移约束和绕x和y轴的转动约束，如图2所示。前三个分析步是对高强螺栓施加预紧力，具体过程为先施加1 kN的螺栓预紧力，然后施加到144 kN，之后将螺栓固定在当前长度，根据试验实际加载程序对柱顶进行位移加载。

2 有限元模型验证

选取文献[10]中试件TJ3、TJ5和文献[11]中试件TJ2进行有限元模型验证，其中TJ3和TJ5分别为CLT板宽为800 mm和1 000 mm的SCLTC组合节点，而TJ2为CLT板上下均有钢板搭接的情况。图3为模拟曲线与试验曲线对比。由图3可见，荷载-挠度模拟曲线与试验曲线总体上较吻合，但是试件TJ2、TJ3的模拟曲线的初始刚度和极限荷载略高于试验值，可能是由于试验中材料自身缺陷、试件制作误差及模型简化处理导致。另外，由于试件尺寸较大，试件数量有限也可能导致误差。表3给出了具体的试验值与模拟值。图4为试验节点TJ3的破坏模式与有限元模型应力云图对比。试验过程中，钢梁的受压翼缘出现屈曲；CLT板上的螺栓孔出现明显的扩孔现象；钢梁端板焊缝断裂。由于在模型中对钢梁和端板进行绑定处理未出现焊缝断裂外，其他破坏特征均在有限元模拟变形中得以体现。通过曲线和破坏模式的对比分析可知，本文所建立的有限元模型总体上能够有效地预测SCLTC组合节点在负弯矩作用下的力学性能。因此，在此基础上，对SCLTC组合节点进行参数化分析。

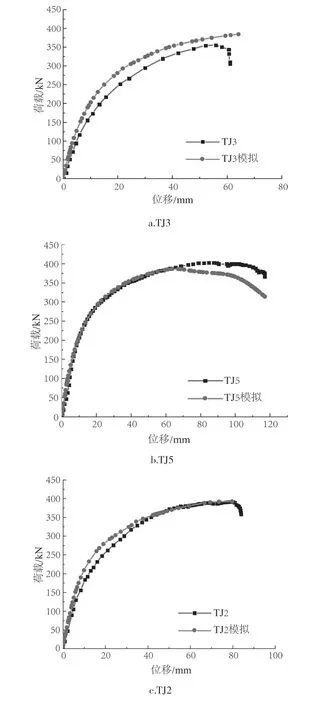
图3 文献试验曲线与模拟曲线对比[10-11]Fig.3 Comparison between simulated curves and test curves from literature[10-11]

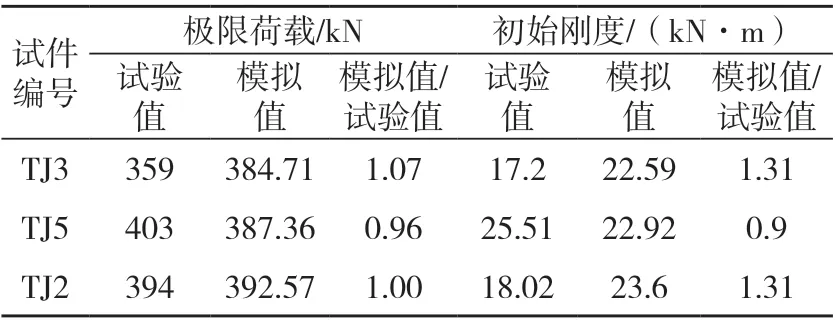
表3 有限元和试验结果对比Tab.3 Comparison between FE simulated results and test results

图4 试验和有限元分析破坏模式的对比Fig.4 Comparison of failure mode between experiment and FE analysis

3 参数影响分析

已有带混凝土楼板的组合节点研究表明，楼板配筋率、厚度、有效宽度及楼板与钢梁之间的剪力连接件等对组合节点的转动性能影响显著[15-18]。鉴于此，为明确不同参数对SCLTC组合节点的转动性能的影响规律，尤其是CLT楼板对节点转动承载力及转动刚度的贡献，对9组共24个SCLTC组合节点进行有限元模拟。主要参数涉及CLT板厚度和宽度、CLT板拼接构造及楼板-钢梁连接构造等。具体参数设置如表4所示。

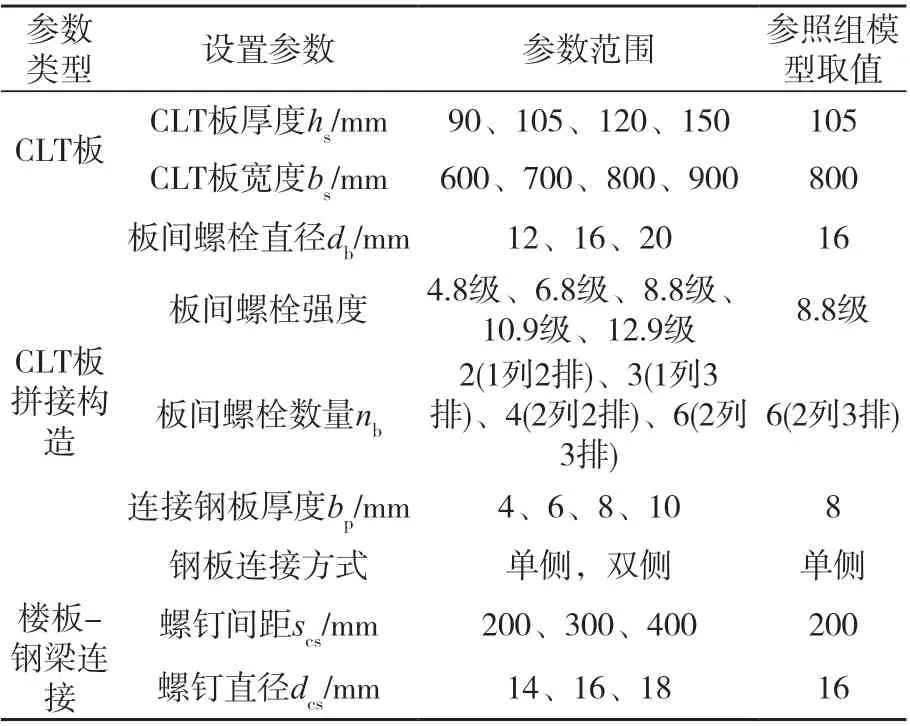
表4 分析参数设置Tab.4 Details of analytical parameters

根据已有文献结果和前文模拟曲线相关研究，该组合节点的力学行为曲线无明显的屈服拐点。因此，本文采用能量等值法[19]计算屈服弯矩，如图5所示。其中，Mu和My分别为极限弯矩和屈服弯矩；θu和θy分别为极限转角和屈服转角。

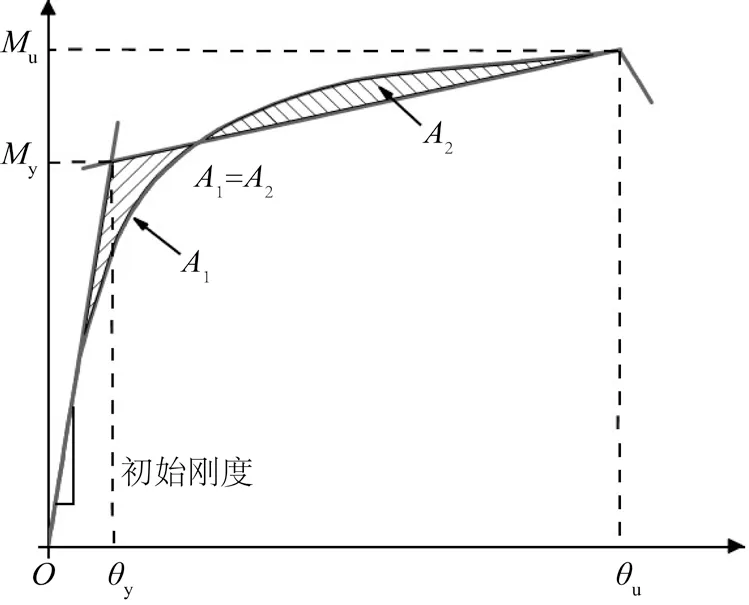
图5 能量等值法[19]Fig.5 Energy equivalence method[19]

3.1 CLT板

以105 mm厚为基准，另选取90、120 mm和150 mm三种厚度进行对比，其中90、105 mm为三层组坯，120、150 mm为五层组坯。120 mm厚CLT板参考文献[25]组坯方式，即中间层板厚度为40 mm，外层层板厚度均为 20 mm。图6为不同CLT厚度和宽度下组合节点的弯矩-转角曲线。表5给出了不同板厚与板宽下组合节点的弯矩-转角特征值。CLT板厚度由hs=90 mm增加至150 mm时，极限弯矩、屈服弯矩和初始刚度分别提高了13.37%、17.8%和22.07%。关于极限弯矩Mu和初始转动刚度Ki的回归公式为：

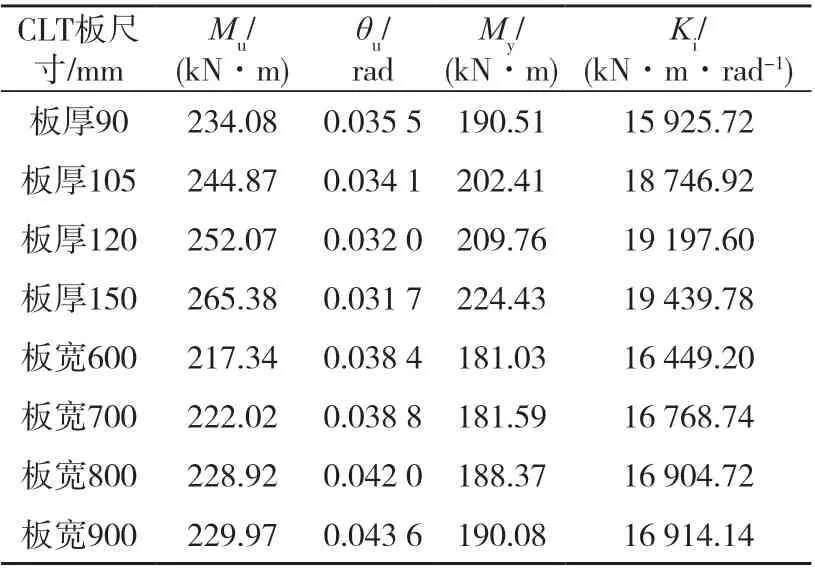
表5 不同板厚和板宽下组合节点弯矩-转角特征值Tab.5 Moment rotation eigenvalues of composite joints with different CLT thicknesses

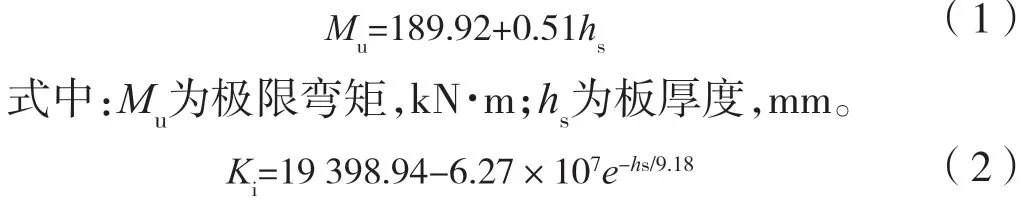
式中：Ki为初始转动刚度，kN·m/rad。

当仅增加CLT板的宽度而搭接钢板不相应加宽时，对SCLTC组合节点的承载力和刚度影响很小。若CLT板和搭接钢板宽度同步增加，极限弯矩和初始刚度均有所提升，如图6b所示。当CLT板宽度增加到bs=800 mm以上时，其极限弯矩和初始刚度几乎不再增加。关于极限弯矩Mu和初始转动刚度Ki的回归公式为：

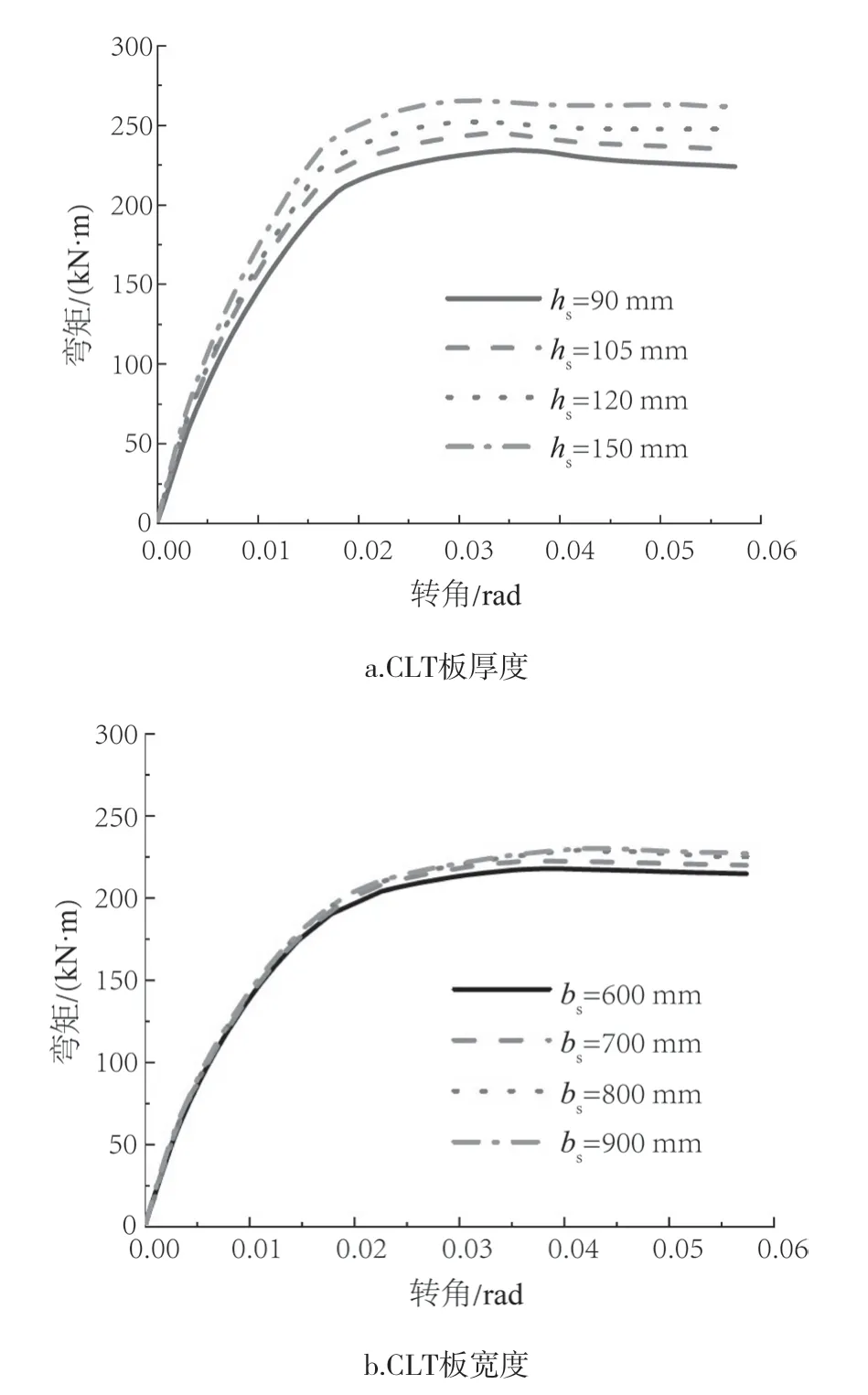
图6 不同CLT板厚与板宽的组合节点弯矩-转角曲线Fig.6 Moment rotation curves of composite joints with different thicknesses and width of CLT slabs

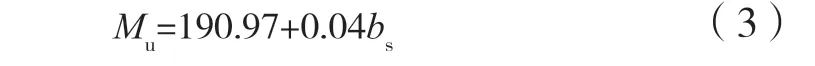
式中：bs为板宽度，mm。

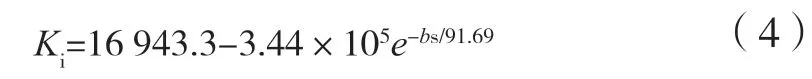
3.2 CLT板拼接构造

CLT板拼接处共选择了五个参数进行分析。图7为不同板间螺栓直径和数量的组合节点弯矩-转角曲线。螺栓直径由db=12 mm增至20 mm时，极限弯矩、屈服弯矩和初始刚度提高了11.07%、13.84%和8.72%。表6显示出了不同板间螺栓直径和数量下组合节点的相关特征值，关于极限弯矩Mu和初始转动刚度Ki的回归公式为：

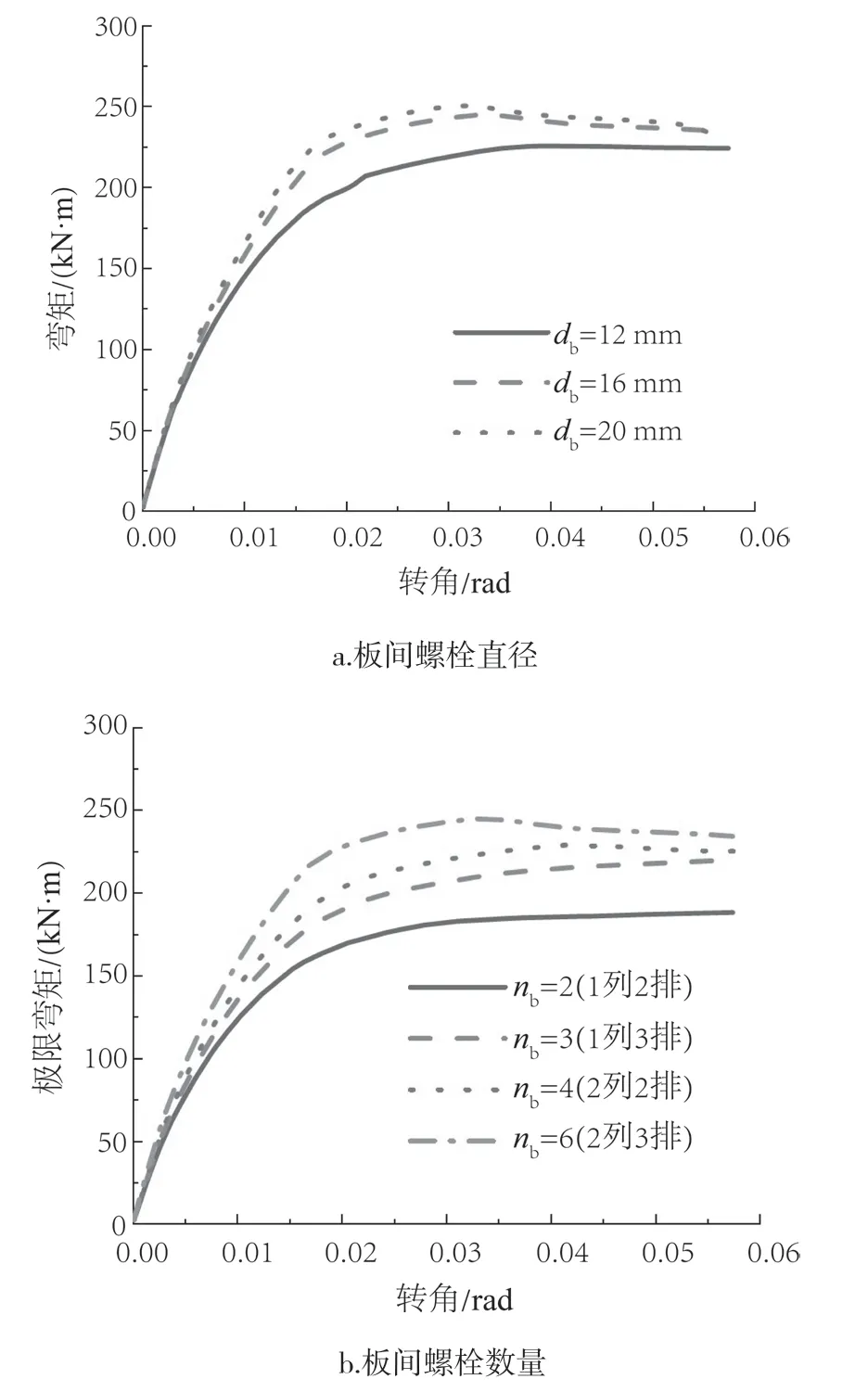
图7 不同板间螺栓直径和数量下组合节点弯矩-转角线Fig.7 Moment rotation curve of composite joints with different bolt diameters and numbers between CLT slabs

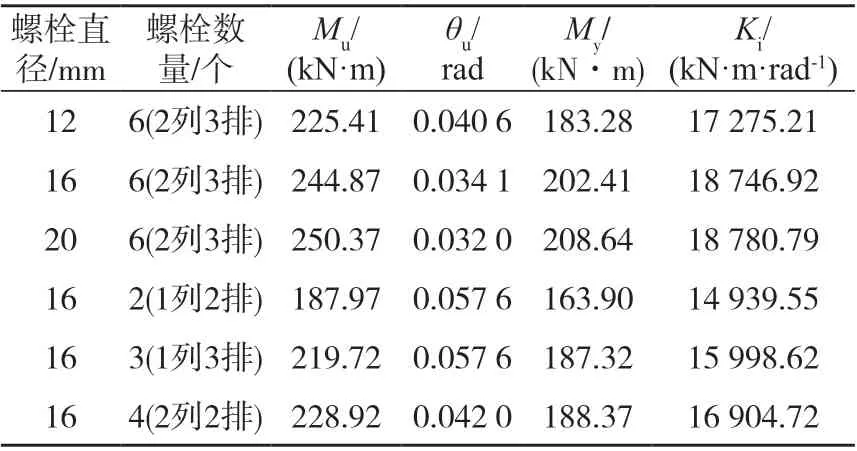
表6 不同板间螺栓直径和数量下组合节点弯矩-转角特征值Tab.6 Moment rotation eigenvalues of composite joints with different bolt diameters between CLT slabs

紧固件数量的增加可提高节点的性能[20]，如图7b所示，当连接钢板单侧的螺栓数量从nb=2（1列2排）增加到nb=6（2列3排）时，极限弯矩、屈服弯矩和初始刚度分别提高了30.27%、23.50%和25.49%。关于极限弯矩Mu和初始转动刚度Ki的回归公式为：

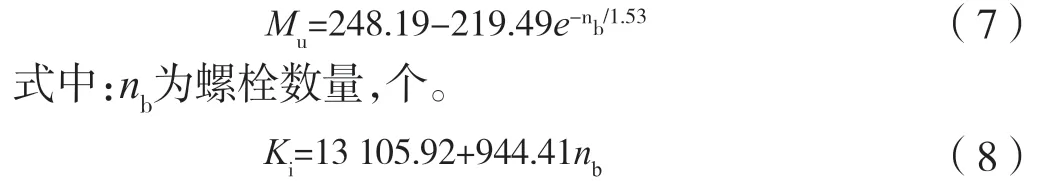
由图8a和b可见，螺栓强度和连接钢板厚度对节点极限弯矩和初始刚度几乎无影响，主要由于当节点进入屈服时，板间螺栓和连接钢板未屈服。CLT板间连接方式选取了单/双侧钢板连接两种。由图8c可知，双侧钢板连接对于单侧钢板连接初始刚度和极限弯矩均略有提高。因为当CLT板向两边受拉时，钢板的连接阻碍了CLT板向外扩张的趋势使得节点性能得到提升，而最终破坏模式是由于CLT板孔壁处受压扩孔使得承载力下降。

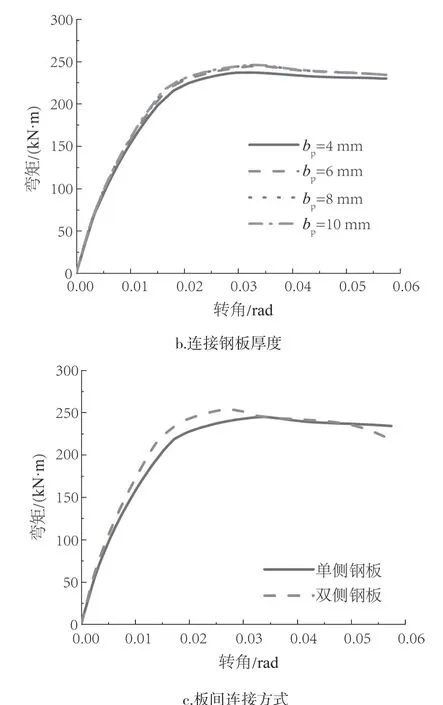
图8 不同CLT板连接处的螺栓强度、钢板厚度和连接方式的组合节点弯矩-转角曲线Fig.8 Moment rotation curves of composite joints with different bolt strength, steel plate thickness and connection mode for CLT spliced joints

3.3 楼板-钢梁连接

剪力连接件是CLT板和钢梁实现共同受力的重要部件。从图9所示的模拟结果可见，剪力连接件的间距和尺寸对SCLTC组合节点的影响很小。这是因为CLT楼板拼接处的强度主要取决于拼接螺栓节点的强度，使得CLT楼板的螺钉处尚未受太大剪力时，CLT板拼接处的木材已经受螺栓的挤压，导致扩孔严重。因此，后期可考虑对CLT板开孔处进行自攻螺钉增强[21]或板间植筋连接[22]。

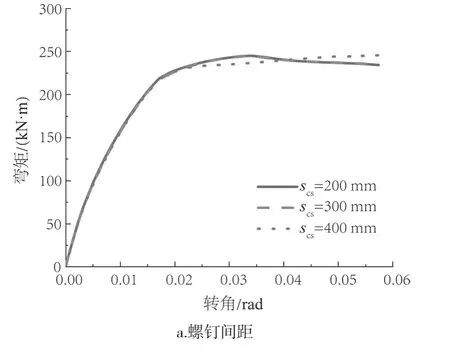
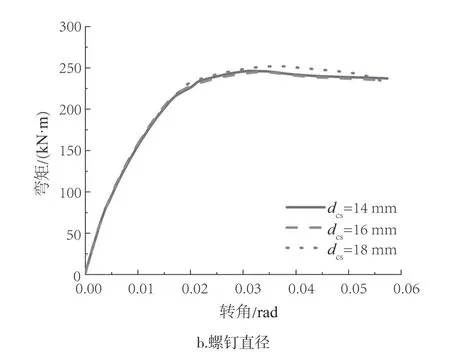
图9 楼板-钢梁处的不同螺钉间距和螺钉直径的组合节点弯矩-转角曲线Fig.9 Moment rotation curves of composite joints with different screw spacing and diameters for floor-steel beam connection

3.4 节点弯矩-转角模型

带CLT楼板的组合节点的数学模型较为直接、有效的方法是试验研究，从而得出弯矩-转角曲线。目前，由于已有SCLTC组合节点的试验样本数量有限，且试验成本较高，本文通过数值模拟与已有试验进行模型验证，在此基础上进行参数研究，进而得出弯矩-转角的数学表达式。钢结构中，梁柱节点的弯矩-转角数学模型主要有线性模型[23]、幂函数模型[24]、多项式模型[25]、指数函数模型[26]、B样条模型[27]等，本文选取Kishi等[28]提出的三参数模型来拟合梁柱节点的弯矩-转角曲线，其表达式为：

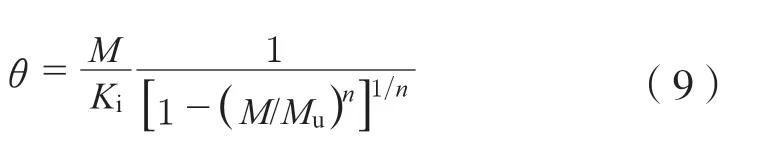
式中：Ki和Mu均通过式（1）～（8）进行计算；n为形状系数。

对于钢结构梁柱节点，部分学者提出节点弯矩-转角关系形状系数的建议值，石文龙等[29]对平端板半刚性梁柱节点的建议值为1.5；对于顶底翼缘角钢半刚性连接节点，施明征等[30]给出的建议值为1.9。本文借鉴钢结构中的研究思路，通过对SCLTC组合节点的弯矩-转角曲线的拟合，建议SCLTC组合节点弯矩-转角关系的形状系数，当n=2时，曲线吻合程度较好，图10为有限元模型和计算模型的对比。

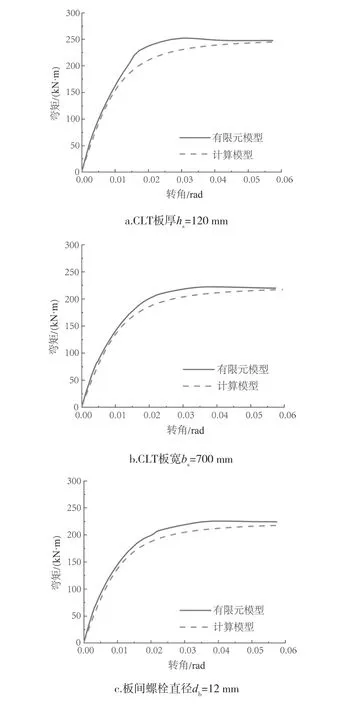
图10 不同参数下弯矩-转角曲线对比Fig.10 Comparison on moment-rotation curves with different parameters

4 结论

本文基于ABAQUS对SCLTC组合节点的负弯矩作用下的力学性能进行了有限元模拟和参数化分析，并和已有的试验数据进行对比；建立了SCLTC组合节点弯矩-转角关系理论模型。主要结论如下：

1）有限元模拟表明，模拟得到的极限承载力和初始刚度与已有文献结果较吻合；已有试验中出现梁端翼缘屈曲，CLT板出现扩孔的破坏模式在模型中有所体现，而钢梁端板焊缝的断裂在模型中破坏不明显。文献中，SCLTC组合节点的屈服特征为梁柱螺栓和板间螺栓开始屈服。

2）CLT板拼接处的相关参数（CLT板的宽度、厚度以及CLT板间螺栓的数量、直径等）对负弯矩作用下的SCLTC组合节点的力学性能比较敏感。其中，CLT板厚度从90 mm增加到150 mm时，组合节点的极限弯矩和初始转动刚度分别提高了13.37%和22.07%；CLT板拼接螺栓数量从2 个（1 列2 排）增加至6 个（2 列3 排）时，组合节点极限弯矩和初始转动刚度分别提高了30.27%和25.49%。剪力连接件的相关参数对节点的力学性能影响较小。

3）通过对SCLTC组合节点转动性能敏感参数特征值的拟合回归，利用三参数模型建立了关于对SCLTC组合节点的弯矩-转角曲线模型，形状系数合理建议值为2。

本研究的目标在于确定影响负弯矩作用下的SCLTC组合节点转动性能的敏感参数，并研究其影响规律；所建立的SCLTC组合节点的弯矩-转角模型，能够为后期有限元模型的简化及钢-CLT楼板组合框架的整体性能分析提供理论指导。