序列堆积杆状药床微细孔道相间阻力特性研究
王禹博,刘东尧
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
现代战争对于火炮高初速、远射程的要求已越来越高,为提高火炮初速与射程,主要采用高能发射药和提高装药的装填密度等技术手段。高能发射药往往有较高的爆温,会加剧对火炮身管的烧蚀,降低身管的使用寿命。因而,较多的关注点转移到了如何提高装填密度。由于多孔杆状药具有燃烧性能突出,可以大幅提升装填密度等特点,近年来被广泛应用在大口径火炮装药设计中,所以多孔杆状药的点火及燃烧得到了广泛的关注。由于多孔杆状药序列堆积排列装药结构使其颗粒间间隙较小,另一方面,杆状药长度远大于常规粒状药,其内孔为微细孔道。因此,点火火焰及燃气在杆状药床中的流动可以看作其在微细孔道内的流动。在两相流的内弹道解算中,火焰燃气与固体颗粒间的相间阻力系数是描述两相相互作用的重要参数之一,杆状药床特殊的装药结构导致相间阻力系数与经典的模型有一定的差异。因此,在杆状药序列堆积装药条件下,气体在其内流动的阻力特性具有重要的理论意义和工程实用价值。
在微细孔道相间阻力领域国内外研究人员进行了大量的实验和数值方面的工作。TURNER等研究了氮气、氦气和空气在硅微通道的流动特性,结果发现在低雷诺数下,阻力系数与雷诺数乘积较低,在高雷诺数下比理论预测要高8%左右。QU等通过实验研究了水力直径为51~169 μm的梯形硅微通道中的水流动特性,实验测得稳态状态下通道的流量和压降,结果表明微通道内的压力梯度和阻力系数均高于传统层流理论。KOHL等通过测量微通道中的压降,并运用合理的数值模型,验证了用于确定平均通道阻力系数的方法。文献[5]分析了可压缩气体在微通道或微管中的流动,而后采用速度滑移和壁面温度跃变边界条件对微通道可压缩流动进行了数值模拟,验证了其分析结果。ZOHAR等采用了摄动展开法对基于流体力学方程的非线性方程进行了解析求解,在已知气体性质的前提下,显式地考虑了滑移流的影响,并与实验对比,验证了理论计算的正确性。GLUZDOV等在压降实验测量的基础上,对矩形截面微通道三维流动进行了数值模拟,给出了阻力系数的关系式。XUE等为解决仿真模型计算量大的问题,建立了一种新的多孔介质理论模型,大大简化了矩形阵列微通道的数值模拟过程,并与实验对比,验证了正确性。赵继鹏等研究了微尺度气体充分发展段流动阻力特性,建议结合Micro-PIV可视化技术和数值手段研究相关复杂机制。李伟卿等对流体在内径为8.2 mm,管长1 m的圆管中的流动阻力特性进行仿真,结果表明随着雷诺数增加,沿程阻力系数越来越小,且下降得越来越慢。
目前,在杆状药序列装填状态下,燃气流动的阻力特性缺少相应的实验数据,本文设计并搭建氮气在相应微细孔道内的流动实验,通过仿真计算与实验比较,寻找合适的模型计算燃气在微细孔道内的流动阻力特性,并将计算数据进行处理,总结出相应关系式。
1 实验装置及数据处理方法
1.1 实验装置
图1为气体在微细孔道中的流动阻力特性实验原理示意图,氮气瓶中的高压氮气经减压阀后,以小于1.0 MPa的压力进入精密调压阀GPR40008H,进行精密稳压后进入MF4008型数字气体流量计,氮气经实验段进口流入孔道,在出口排入大气。在实验药柱段进口和出口处利用压力变送器测量进出口压降;流量计与2个压力变送器均与数据记录仪相连显示和保存数据。
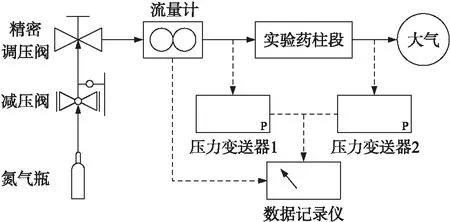
图1 实验原理示意图
其中,实验药柱段内放置单个杆状药或模拟杆状药床,杆状药内孔直径为0.4 mm,长度为50 mm;杆状药床采用序列堆积排列状态下杆状药间隙结构,其局部的截面如图2所示。按照杆状药局部截面结构,通过3D打印技术制作出模型,杆状药颗粒花边结构形成的间隙可分成两类,可近似为三角形和四边形。

图2 杆状药床孔道截面模型图
1.2 数据处理方法
本实验测量孔道进出口两端压降与质量流量,通过质量流量导出微通道内流体速度,将已知量代入相关公式,比较阻力系数与雷诺数之间的关系。
由流体力学可知,对于微通道内气体流动,有:

(1)
式中:Δ为对进出突缩和出口突扩进行修正后的压降,为阻力系数,为微通道长度,为微通道直径,为微通道内流体密度,为流体速度。
由式(1)可知:
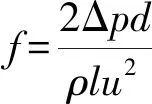
(2)
由于氮气密度随压力变化较大,雷诺数采用下述公式计算:

(3)
式中:为运动黏性系数,取相应进出口压力下运动黏性系数的平均值。
实验所用精密调压阀精度等级为0.5%;流量计精度等级为1.7%;压力变送器为赫斯曼标准型压力变送器,精度等级为0.5%。根据所选用仪表特性以及误差原理,实验结果总误差在5%以内。
1.3 实验结果与分析
首先,封闭颗粒间不规则间隙,研究杆状药内孔气体流动阻力特性。整理实验数据,并将所需参量代入式(2)与式(3)中,得到阻力系数与雷诺数,雷诺数在2 000~20 000范围内,杆状药内孔相间阻力系数随着雷诺数的增大不断降低,进行拟合后得到:
=1685×10-2018
(4)
然后,封闭颗粒内孔,研究杆状药颗粒间间隙气体流动阻力特性,由于颗粒间间隙为不规则流动通道,引入当量直径表达式为
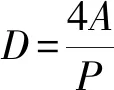
(5)
式中:为不规则流动通道的截面积,为不规则流动通道的湿周,计算得到当量直径为0.453 mm。
经过对实验数据处理,对雷诺数与阻力系数的关系进行拟合,在雷诺数2 500~25 000范围内,得到:
=2641×10-2026
(6)
可以看到花边形形成的不规则间隙虽有较大的当量直径,但其阻力系数大于圆形内孔。
最后,对同时含有内孔和颗粒间隙的孔道结构进行实验,计算得到当量直径为0.432 mm,在雷诺数1 000~15 000范围内,得到:
=2094×10-2018
(7)
同样可以发现,杆状药床的阻力系数介于圆孔和非规则结构间隙之间。3种情况下阻力系数与雷诺数的关系如图3所示。
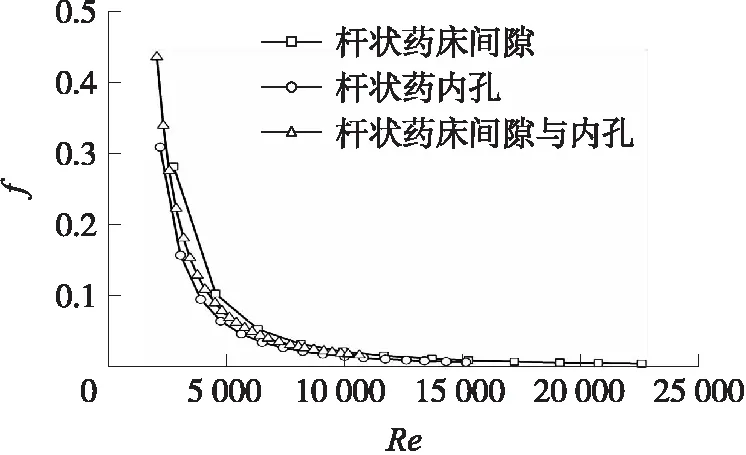
图3 3种情况下的雷诺数与阻力系数点线图
2 氮气在杆状药床间流动仿真分析
由于实验过程存在不可避免的误差,影响因素较为复杂,所以同时需要采用仿真计算杆状药序列堆积装药阻力系数与雷诺数的变化关系,并与实验结果对比。
2.1 网格划分
本文选用Fluent进行仿真分析,与实验进行对比。利用Meshing对模型进行网格划分。首先进行网格无关性验证。在单个杆状药中选取单孔进行仿真,选取工况进口压力为0.190 MPa,采用网格数由9 804至99 852进行计算,相对误差从2.79%降至0.18%,如表1所示,为节省计算资源,选用网格数为81 624进行其余工况计算。杆状药床的间隙仿真选取整体的1/6,网格无关性验证与上述相同,此处不再赘述,最终选取网格数量为215 348。

表1 网格无关性验证
2.2 Fluent条件设置
在选取合适的网格后,导入Fluent对模型进行求解,具体设置如下:
①由于氮气、混合燃气为可压缩气体,选用密度基求解;
②实验得到的微细孔道气体流动雷诺数大于1 000,选择-湍流模型进行计算;
③孔道进口和出口边界由实验所测量的压强给出;
④由于需要考虑流动充分发展段,避免计算提前结束,故残差设置为10。
2.3 计算结果与分析
2.3.1 氮气在杆状药内孔流动仿真
以某一实验工况为例,对氮气在孔道内的流动进行数值仿真,相对于大气压取进口压力=0.190 MPa,出口压力=0,计算得到杆状药内孔压强变化云图如图4所示。
由图4可以看出,氮气进入孔道后,从进口到出口压强逐渐降低,由于孔道突缩,在进口处有明显的压强损失。该进出口压强条件下计算所得流量与实验测量值对比,误差小于5%。

图4 进口压力为0.190 MPa时杆状药内孔压强分布
2.3.2 氮气在杆状药床间隙流动仿真
同样,取实验工况相对大气压进口压力=0.2 MPa,出口压力=0进行计算,得到孔道内压强分布如图5所示。同样由图5可以看出,氮气在杆状药床间隙的流动与杆状药内孔流动趋势基本相同,从进口到出口,气体压力逐渐降低,且在进口处同样存在较大的压力损失。该进出口压强条件下,计算所得流量与实验测量值对比,误差小于5%。上述计算结果说明采用的模型和计算方法较为合理。

图5 进口压力为0.20 MPa时药床间隙压强分布
2.4 结果与分析
由于需要进行误差分析,引入平均相对误差(MAE)来衡量仿真结果与实验计算结果的偏离程度,其计算公式为

(8)
式中:为平均相对误差,()为仿真计算值,()为实验结果,为数据个数。
按上述计算方法,对杆状药内孔阻力系数各实验工况进行仿真,在给出相同的进出口压力下,计算得到的阻力系数平均相对误差为4.87%。同样,对杆状药床间隙阻力系数各实验工况进行仿真,在给出相同的进出口压力下,计算得到的阻力系数的平均相对误差为9.56%。将3种情况下计算所得阻力系数进行比较,如图6所示,在相应工况下,计算得到的阻力系数略高于实验结果,且数据基本都在-10%~10%误差线以内。对于误差产生原因,一方面由于实验中测得压力略高于实际入口压力,另一方面也不排除数值仿真中模型的选择及近壁边界层的处理。
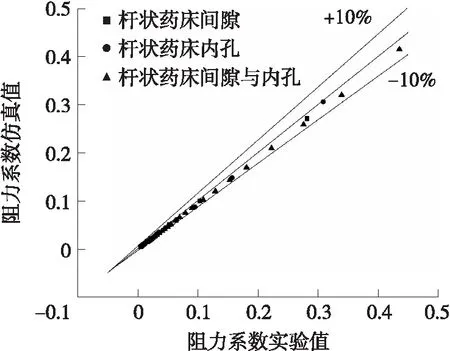
图6 仿真计算与实验结果的阻力系数对比
3 火药燃气在杆状药床内流动仿真分析
高温状态下的火药燃气组成及物性与实验所用的氮气有一定的区别,采用氮气作为工质在上一节模型中仿真结果与实验吻合较好,本节采取上述模型计算火药燃气在杆状药床中的流动特性。
本文使用花边形十九孔火药为三基药,其燃烧生成的气体为不同组分气体组成的混合气体,具体成分如表2所示。在Fluent计算中将氮气调整为火药燃气,其物性参量用混合物参量表示。计算条件设置与氮气相同,进口压力范围不超过实验中测得的最大范围,具体计算结果如下。计算得到的火药燃气出口速度与进出口压差Δ关系如图7所示。由图7可以看出,几种孔道条件下,燃气出口速度与进出口压差基本上成正比关系,这种趋势与氮气类似。同样可以看到,在相同的压差条件下,火药燃气在杆状药床的出口速度介于其在杆状药床间隙与杆状药单个内孔之间,其在杆状药床间隙的出口速度相比于其余两种情况较大,3种情况的规律与氮气在实验中得到的规律基本相同,同等条件下,火药燃气的出口速度大于氮气的出口速度。

表2 火药燃气组成成分
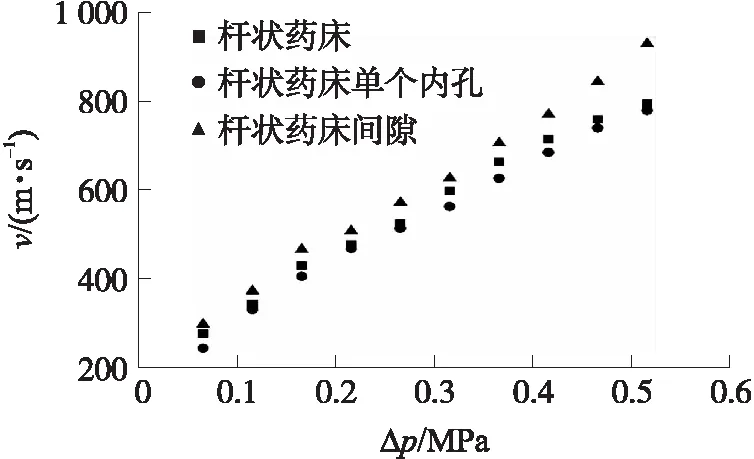
图7 出口速度随进口压力变化示意图
将火药燃气在孔道3种情况下的仿真数据进行处理,得到的阻力系数与雷诺数关系如图8所示。由图8可知,3种孔道情况下的阻力系数都是随着雷诺数增大而减小,且在同等雷诺数下,杆状药间隙的阻力系数较大。相较于氮气,火药燃气的阻力系数有所降低。
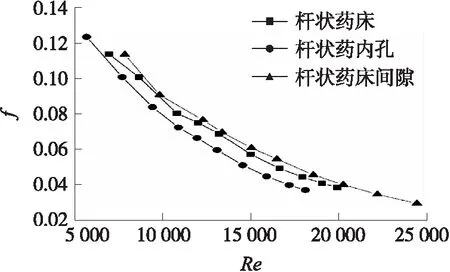
图8 3种情况下阻力系数与雷诺数关系
将图8中火药燃气在杆状药床流动的阻力系数与雷诺数的关系进行拟合,可以得到如下公式:
=4854-0953 4
(9)
式(9)可以用于求解内弹道一维两相流的辅助方程,具体应用在多孔杆状药燃烧的初期,即火药燃气在多孔杆状药内孔中流动加热整个药床的过程中,在杆状药加热到一定温度开始燃烧后,其内孔孔径会不断增大,此时需选择其他经验公式进行计算。
4 结论
本文在实验的基础上,测量氮气在杆状药内孔、药粒间隙及药床孔道内流动时的压降与质量流量,并计算出阻力系数与雷诺数的关系;随后对氮气在杆状药内孔及药粒间隙内的流动、火药燃气在杆状药内孔流动进行了仿真分析,计算相应的阻力系数,得到以下结论:
①对于杆状药内孔,雷诺数在2 000~20 000范围内,随着进出口压降不断变大,质量流量不断增大,根据实验数据进行拟合,可以得到氮气在内孔流动阻力系数与雷诺数的关系式为=1685×10-2018。
②对于杆状药颗粒间隙,在雷诺数为2 500~25 000范围内,对不同进出口压降和质量流量的实验工况进行分析,可以总结出氮气在颗粒间隙流动阻力系数与雷诺数的关系式为=2641×10-2026。
③同时包含杆状药内孔及颗粒间隙的药床,雷诺数在1 000~15 000范围内,可以得到氮气在药床间流动的阻力系数与雷诺数关系为=2094×10-2018。
④采用软件对氮气在杆状药内孔及颗粒间隙流动进行仿真计算,在相同的压降下,仿真计算得出阻力系数随雷诺数的变化规律与实验结果基本一致;计算得到的阻力系数略低于实验值。
⑤在相同模型下,数值计算得到的燃气在杆状药床中流动阻力系数与雷诺系数关系式为=4854-09534,此式可作为辅助方程计算内弹道过程中杆状药燃烧前加热时的相间阻力系数。

