永磁式电磁阻尼器磁性能解析计算及阻尼特性分析
梁仕民,杨国来,李加浩,王丽群,张弘毅
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国计量大学 机电工程学院,浙江 杭州 310018;3.湖南大学 土木工程学院,湖南 长沙 410082)
液压式制退机具有结构复杂、维护困难和易出现液体泄漏等问题,而电磁阻尼器具有结构简单、非接触式和无污染等优点,因此,将电磁阻尼器应用在火炮反后坐装置中具有重要的工程意义。根据初级激励源不同,电磁阻尼器主要分为电励磁式、混合励磁式和永磁式,电励磁式和混合励磁在强冲击载荷下需要外部电源进行供电,具有体积大、结构复杂和效率低等缺点,不适合火炮反后坐装置的可靠性和轻量化要求,而永磁式电磁阻尼器不需要额外供电与线圈绕组,具有体积小、可靠性高等优点,在强冲击载荷下能够满足火炮的后坐阻力和后坐位移要求。Halbach永磁阵列具有良好的自屏蔽性能且用少量的磁体就能产生较强的磁场,将该永磁阵列应用于电磁阻尼器中能够解决永磁体一侧漏磁问题。李启坤等通过有限元仿真软件分析在强冲击载荷下Halbach电涡流阻尼器的动力学特性及永磁体发生同轴偏差时对涡流阻尼力的影响情况,但缺少对模型准确性验证。
分层理论法能较准确地计算出永磁式电磁阻尼器的磁场,揭示电磁阻尼器性能与电磁阻尼器参数之间的联系。KOU等提出了一种永磁式直线电涡流制动器,利用分层理论推导了电涡流制动器的解析模型,并采用有限元法对制动力特性进行了分析。尹相睿推导永磁直线涡流制动器的磁场分布及力特性方程,并分析其端部效应对磁场和涡流的影响。LI等利用分层理论对高加速度下平板型电涡流阻尼器的制动力进行计算,分析准静态和高加速度条件下阻尼力的变化规律。文献[7-9]对平板型电磁阻尼器磁场特性进行了分析,但未分析边界效应对磁场的影响,而圆筒型阻尼器能量利用率更高,不存在横向边界效应影响。CHEN等提出了一款圆筒型磁阻尼器用于解决力传感器振动问题,利用能量法和等效伪刚体模型对电涡流阻尼器进行动力学分析,同时建立计算磁场分布和阻尼系数的解析模型,其模型分为导体、气隙和永磁体3个区域,未考虑其余区域对磁场带来的影响。相较于CHEN等提出的结构,本文采用的圆筒型永磁式电磁阻尼器在充分考虑磁场分布与温度扩散的影响下存在6个子域,分别为运动导杆域、隔热层域、永磁体域、气隙域、导体内筒域与外筒背铁域。其中外筒背铁域用于提供磁场的外回路,提高了源磁场的利用率;运动导杆域将磁场的内回路考虑其中;隔热层避免了身管传热对永磁体磁性能带来的影响。
本文采用圆筒型Halbach永磁式电磁阻尼器方案,通过分层理论将其按结构划分每个区域,根据不同区域的磁场关系推导出内筒区域的磁感应强度和后坐过程中产生的电磁阻尼力。建立电磁阻尼器有限元模型,与解析模型互相印证。引入火炮后坐运动方程,计算在强冲击载荷时电磁阻尼器的阻尼特性,并通过有限元分析考虑磁性饱和情况下电磁阻尼力随内筒厚度的变化规律。
1 Halbach永磁阵列电磁阻尼器模型建立与分析
1.1 圆筒型永磁式电磁阻尼器
永磁式电磁阻尼器主要由外筒背铁、导体内筒、隔热层、永磁体和运动导杆等组成,其结构简图如图1 所示。

图1 圆筒型永磁式电磁阻尼器局部视图
图1所示阻尼器的工作原理为当火炮发射发生后坐运动时,运动导杆、隔热层和永磁体产生主磁场作为初级,内筒和外筒作为次级,当初级和次级发生相对运动时,由楞次定律可知,次级产生涡流从而产生电磁力阻碍初级的相对运动。
1.2 分层理论解析模型建立
应用分层理论求解磁场的电磁性能时,将解析模型分为6个求解区域,以为旋转轴线的圆柱体剖面简图如图2所示,图中区域Ⅲ为Halbach永磁阵列,箭头方向为永磁体的充磁方向。

图2 分层理论解析求解区域
为简化分析求解过程,做如下假设:
①模型在方向无限长;只存在环绕导体内筒的涡流,且不考虑涡流产生的趋肤效应。
②气隙磁感应强度在方向上为恒定值,不计端部效应。
③导体内筒及永磁体的相对磁导率为1。
由麦克斯韦方程组可得:

(1)

(2)
式中:为磁场强度,为电流密度,为磁通量密度,为电场强度。
由磁场本构关系可得:
=
(3)
电流密度:
=σ
(4)
式中:为空气磁导率;为相对磁导率;内筒导体的电导率=387×10S/m。
当内筒与外筒结合且一起以速度运动时,导体内筒会产生涡流,得:
=(+×)
(5)


(6)
由式(1)、式(3)和式(6)推导可知:

(7)
为了简化计算,将4个不同充磁方向的永磁体作为一个整体,由傅里叶级数可得磁矢势的表达式为

(8)
式中:=π,电磁阻尼器极距=+;径向充磁方向永磁体长度=20mm;轴向充磁方向永磁体长度=15mm。
因为区域Ⅰ、Ⅱ、Ⅳ、Ⅵ的电导率为0,由式(7)可知:

(9)
式中:代表Ⅰ,Ⅱ,Ⅳ,Ⅵ。
对于区域Ⅲ永磁体阵列区域,永磁体的本构关系用剩余磁通密度来表示:
=+
(10)
式中:为永磁体剩磁,大小为145 T,剩磁在和方向分别为径向剩磁和轴向剩磁。
=res,+res,
(11)
由式(1)、式(7)、式(10)和式(11)可得:

(12)
在区域Ⅴ处,由于导体内筒的电导率不为0,导体内筒以速度运动,则由洛伦磁力可得:
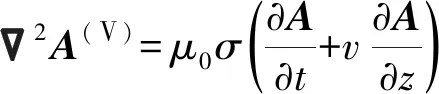
(13)
右边的左侧项为感生电动势,右侧项为动生电动势,在计算运动情况下不计及感生电动势,因此式(13)可表示为

(14)
由拉普拉斯算子在圆柱坐标系下的表示法得每个区域的解析式为


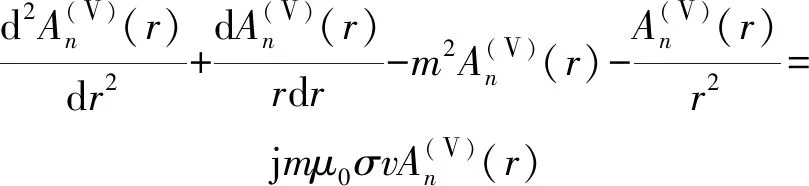



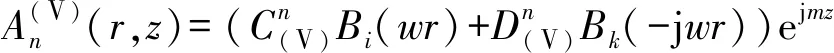
式中:和是由边界条件确定的常数,和为不同类别贝塞尔函数,为非齐次贝塞尔方程解。在相邻区域的边界上,磁通密度的法向分量是连续的,磁场强度的切向分量是连续的。
设=745 mm,=1345 mm,=1375 mm,=1670 mm,=1690 mm,=1705 mm。
在法向的边界条件,即1=2:

在切向上的边界条件,即1=2:

式中:运动导杆导磁系数、隔热层导磁系数和背铁导磁系数均为600。
通过对磁矢势的求解,可以得到内筒导体内的磁通密度和涡流分布:
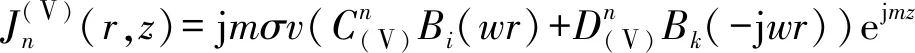
由高斯定理可求得柱坐标下矢量场在不同坐标系中旋度的表达式:

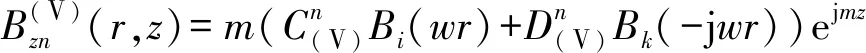
由上述公式可求内筒处轴向电磁阻力:

1.3 有限元模型建立
为了验证解析模型的准确性,建立圆筒型Halbach永磁阵列电磁阻尼器的有限元模型,如图3所示,图中自下而上分别是空气域、运动导杆、隔热层、永磁体、气隙、导体内筒、外筒背铁和空气域。电磁阻尼器的结构是由多个旋转体组成,为简化计算,选用二维轴对称的计算模式进行分析。由于永磁阵列在轴向的长度是有限的,为了消除端部效应对结果的影响,有限元模型计算的结果选自永磁阵列处中间一个周期进行分析,本构关系的选择与解析模型一致。

图3 有限元仿真模型
在有限元法中,瞬态磁场仿真可以求解非恒定磁场中初级与次级的相对运动情况,通过赋予内外筒一个稳定增长的速度,观察初级与次级发生相对运动时电磁阻尼器的变化情况,计算磁感应强度和电磁阻尼力。
1.4 模型验证
对导体内筒(=(-)2)处的磁感应强度随轴不同位置的变化规律分别进行了有限元和解析求解,对比结果如图4所示。在速度为0时,磁感应强度曲线在径向充磁方向的永磁体处呈现出平缓的曲线,但在速度为12 m/s时,由于涡流去磁的作用使得平缓的曲线变为一个极值,从2种方法的结果对比可以看出吻合效果较好。

图4 导体内筒处径向磁感应强度与位置曲线
后坐阻力和速度之间的关系如图5所示。可以看出,解析模型的解与有限元模型解变化规律一致,且最大误差为5.47%,在可接受范围内,由此可得当速度增加到一定值时,电磁阻尼力的增加不再随速度的增加而增加,此时所对应的速度值称为临界速度值,当后坐速度超过临界速度值时,电磁阻尼力会随着速度的增加而减小,因此在设计电磁阻尼器时,应确保后坐速度不会超过临界速度值,否则会在火炮后坐过程中造成不可避免的损坏。

图5 后坐阻力与后坐速度的关系
2 强冲击载荷下阻尼特性分析
2.1 电磁阻尼器的后坐运动分析
引入火炮的后坐运动方程,编写某大口径火炮炮膛合力载荷激励函数和根据火炮的复进要求选定复进机的类型,后坐过程中炮膛合力曲线和复进机的后坐行程函数曲线如图6和图7所示。

图6 炮膛合力曲线

图7 复进机力曲线
将上述曲线作为电磁阻尼器的激励函数,得到电磁阻尼器在强冲击载荷下后坐运动过程响应,如图8所示。从图8中可以看出,在后坐位移到达100 mm左右时,后坐速度处于最高速度,约为12.4 m/s,同时电磁阻尼力也达到峰值,整个后坐行程约为740.5 mm。由图5可知,在强冲击载荷的后坐过程中,其最大后坐速度未超过临界速度。

图8 强冲击载荷下后坐运动过程响应
在强冲击载荷作用下,电磁阻尼器产生的阻尼力如图9所示,产生的电磁阻尼力峰值约为530 kN,有限元与解析法产生的结果最大误差为2.59%,整个后坐过程时间约为150 ms。

图9 电磁阻尼力有限元法与解析法对比
2.2 不同结构参数对电磁阻尼力的影响
当电磁阻尼器设计完成后,其能够承受的最大阻尼力、临界速度等也随之确定。因此在设计电磁阻尼器前,需要研究不同结构参数对电磁力的影响规律。
由于空气中的磁阻远大于内筒,所以不同的气隙宽度对电磁阻尼力的影响均不同。电磁阻尼力随气隙宽度的变化规律如图10所示。可知,当内筒与永磁体之间的气隙越小,产生的电磁阻尼力也会越大,且后坐运动所需要的时间也越短;气隙越大,电磁阻尼力越小,后坐运动所需要时间越多。在理想情况下,虽然气隙宽度越小,其产生的阻力也会随之增加。但是,气隙宽度减小会同时增加加工难度并影响散热,因此,在设计时应综合各种因素合理选择气隙宽度。
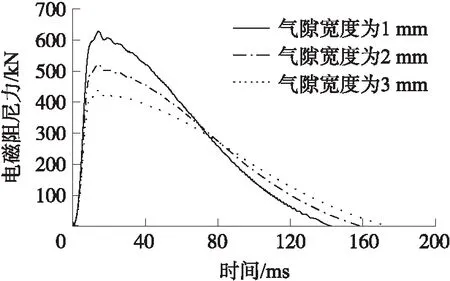
图10 电磁阻尼力随气隙宽度变化规律
在解析法中考虑磁性饱和情况非常困难,为确保有限元仿真结果更贴近实际,在有限元仿真中考虑背铁的磁性饱和情况,即背铁磁化强度达到某一值时,外磁场强度增强而磁化强度不再增加。从图11可知电磁阻尼力随内筒厚度的变化规律,在一定范围内,当内筒的厚度增加时,内筒感应出的电涡流面积也随之增加,使得产生的电磁阻尼力增加,随着涡流面积的增加,电涡流产生的磁感应强度增加,涡流产生的磁感应强度与永磁体产生的磁感应强度方向相反,导致磁场中的磁感应强度也随之减少,从而产生退磁现象,电磁阻尼力曲线呈现出“马鞍”型。

图11 电磁阻尼力随内筒厚度变化规律
当内筒厚度较小时并不会出现退磁现象,电磁阻尼力呈现出较为平稳的趋势,但当内筒厚度过小时,涡流面积较小,其产生的电磁阻尼力不能满足后坐需求,故合理选择内筒厚度能够避免退磁现象和电磁阻尼力不足的情况。
3 结束语
利用分层理论推导了磁场的表达式,建立了Halbach永磁阵列电磁阻尼器的解析模型,同时建立有限元分析模型,并进行了互相印证。通过有限元法分析不同的气隙宽度和内筒厚度对电磁阻尼力的变化规律,为电磁阻尼器的设计提供一定的理论参考。但解析模型缺少对磁性饱和、导体内筒温度发生变化而引起阻尼变化的影响,在后续工作中应进一步研究。

