低保标准预测及保障力度分析

李艳春

(吉林建筑科技学院，长春 130114)

1 模型假设

第一，假设题目给定数据真实可靠。第二，假设相关性因素之间互相独立。第三，假设统计的数据真实可靠。第四，假设贫困人口占总人口的比例同城市贫困人口占城市总人口和农村贫困人口占农村总人口的比例不变，则城市贫困人口比例越大，城市人口越多，城市越发达，农村贫困人口比例越大越不发达，越需要补助。第五，农村贫困人口比例与补助标准总额成正比。定义与符号说明如表1所示。

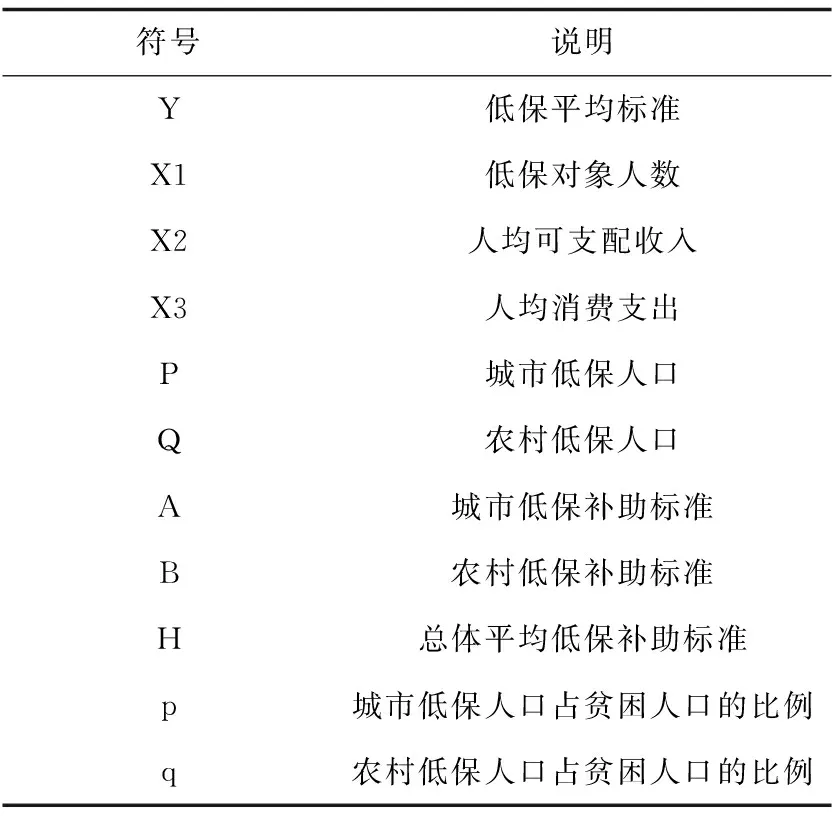
表1 定义与符号说明Tab.1 Definition and symbol description

2 模型的建立与求解

2.1 参数指标

通过查找统计收集北京市2012-2016年统计年鉴的有关参数，如表2所示，选出低保对象人数、人均可支配收入及人均消费支出等参数作为指标。

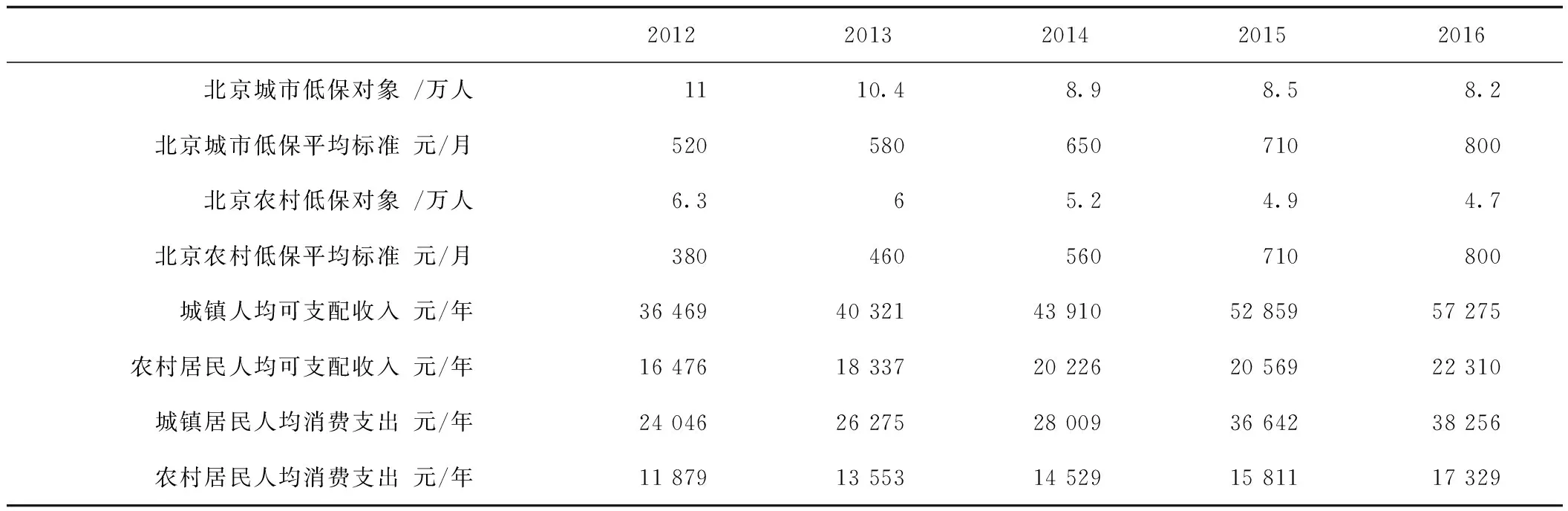
表2 北京市2012-2016年统计年鉴Tab.2 Beijing Statistical Yearbook from 2012 to 2016

2.2 模型的建立与求解

根据题意设城市低保人口P人，农村低保人口Q人，城市低保补助标准为A，农村低保补助标准为B，总体平均低保补助标准为H，p为城市低保人口占贫困人口的比例，q为农村低保人口占贫困人口的比例，则：PA+QB=H(P+Q)

pA+qB=H

农村贫困人口比例q与补助标准总额H(P+Q)成正比，则：

Q/(P+Q)=kH(P+Q)

Q=kH

假设城市低保补助标准与农村低保补助标准只存在一个系数差m，则：B=mA

最后得到：pA+(1-p)mA=(1-p)/k

通过计算每年的m值，取平均得到m=0.57

通过计算每年的k值，取平均得到k=1.2×10＾-4

所以模型如下：pA+0.57×(1-p)A=(1-p)/1.2×10＾-4

经检验，数据处理后如表1所示，该模型建立存在一定误差，贫困补助标准并非传统线性标准模型，需要进一步改进。

2.3 低保标准变化趋势

查找并统计北京市和浙江省两地的数据，通过Excel软件处理后如图1～图4所示。

第一，由图1可知，两地的低保平均标准逐年增长，增长趋势大致相同，2015年开始北京市城镇低保和农村低保开始并轨。

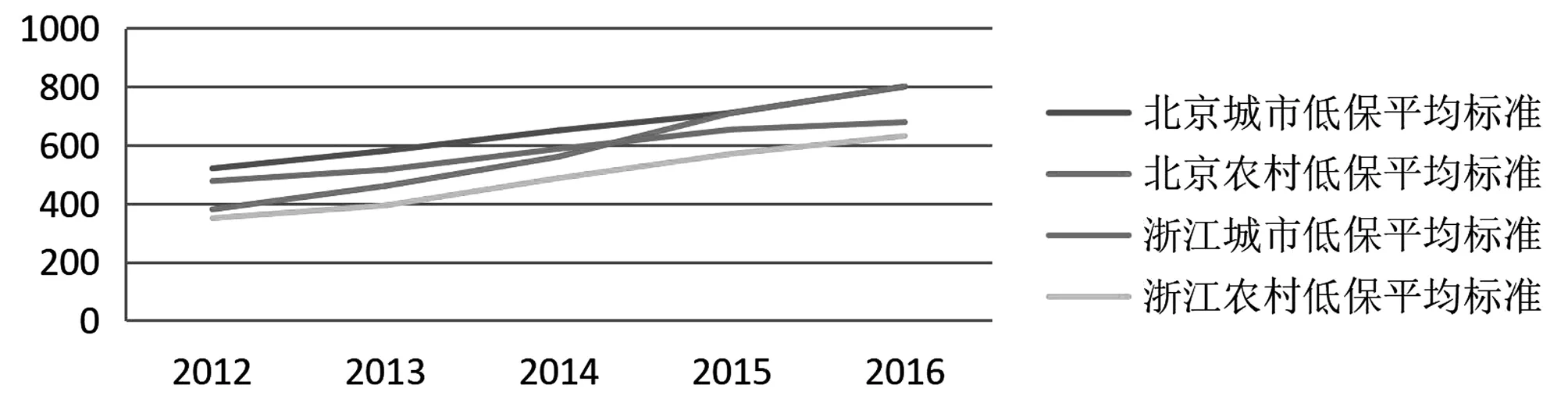
图1 北京市及浙江省2012-2016年低保平均标准趋势Fig.1 Average trend of subsistence allowance of Beijing City and Zhejiang Province from 2012 to 2016

第二，由图2可知，两地的低保对象人数呈波动趋势，由于其基数较大，因此需要考虑其影响。

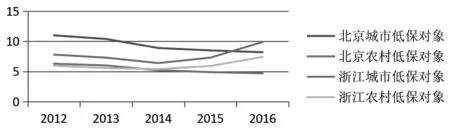
图2 北京市及浙江省2012-2016年低保对象平均标准趋势Fig.2 Average trend of subsistence allowance recipients of Beijing City and Zhejiang Province from 2012 to 2016

第三，由图3可知，两地的人均可支配收入呈现逐年小幅度增长趋势。

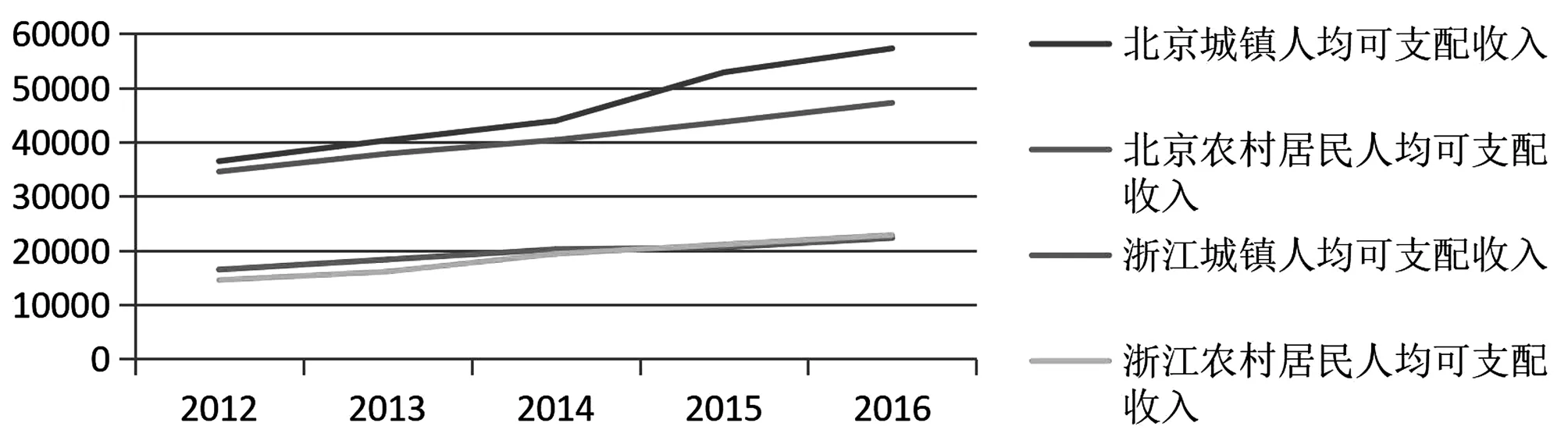
图3 北京市及浙江省2012-2016年人均可支配收入平均标准趋势Fig.3 Average trend of per capita disposable income of Beijing City and Zhejiang Province from 2012 to 2016

第四，由图4可知，两地的人均消费支出也呈增长趋势。

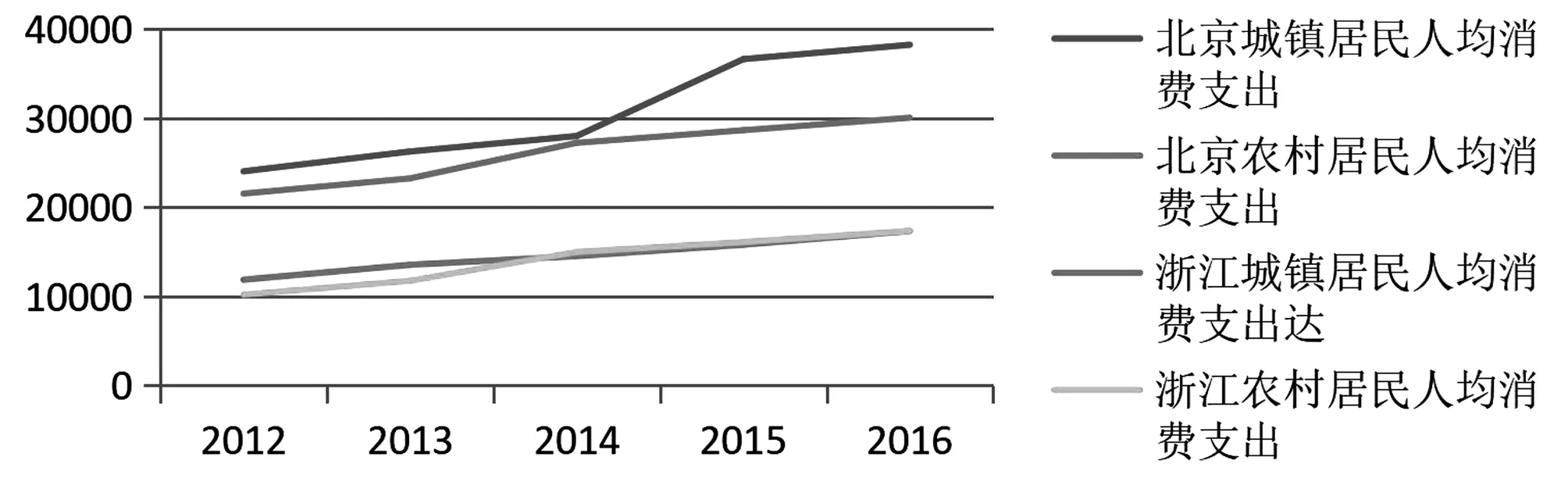
图4 北京市及浙江省2012-2016年人均消费支出平均标准趋势Fig.4 Average trend of per capita consumption expenditure of Beijing City and Zhejiang Province from 2012 to 2016

根据以上数据统计可以看出，北京市和浙江省两地的低保平均标准、低保对象、人均可支配收入、人均消费支出呈大致相似趋势。低保平均标准逐年增长且人均可支配收入及人均消费支出也逐年增长，低保对象人数随着经济的增长也大致呈上升趋势。因此，假设低保平均标准与人均可支配收入、人均消费支出、低保对象人数为多元线性关系。

2.4 检验

2.4.1 模型的建立与求解

通过分析对低保对象人数、人均可支配收入、人均消费支出等参数进行建模，提出如下关于低保标准改进的多元线性模型：

Y=b0+b1X1+b2X2+b3X3

其中，Y表示低保平均标准，X1表示低保对象人数，X2表示人均可支配收入，X3表示人均消费支出，b=(i=0,1,2,3)表示待估计的参数。

对于低保标准模型，将统计的表1数据用于估计模型的参数。

在MATLAB中编写程序得到回归系数估计值及置信区间，相应模型如下：

城市平均低保标准：Y=82.069 6-4.615X1+0.028 2X2-0.022 5X3

得到的R2=1.000 0，残差图如图5所示。

图5 城市平均低保标准残差图Fig.5 Residual chart of urban average subsistence allowance standard

农村平均低保标准：Y=1 075-139.921X1-0.066 6X2+0.107 4X3

得到的R2=0.997 7，残差图如图6所示。

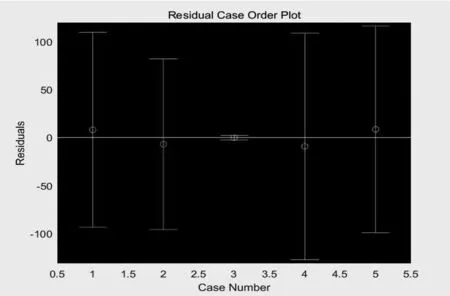
图6 农村平均低保标准残差图Fig.6 Residual chart of the average subsistence allowance standard in rural areas

2.4.2 模型的检验

由于判定系数接近于1，通过残差分析不论是农村还是城市的平均低保标准，所示的残差图效果都良好，比传统的线性回归模型精度更高，更贴近实际值，因此可作为低保标准的参考。

通过统计2017年北京农村及城市低保对象人数、人均可支配收入、人均消费支出等参数，检验模型的合理性，计算得到北京城市低保平均标准为898.136 8

元/月，北京农村低保平均标准为865.157 6元/月，误差比例城市1.002、农村1.040，反映出该模型的建立比较接近实际，残差图显示模型比较逼真。综上，证明建立的模型是合理的。

3 模型的评价

3.1 模型的优点

该模型以人均可支配收入、人均消费支出及低保对象人数等利于统计的数据指标作为变量，建立多元线性模型对低保标准进行拟合，便捷地得出低保标准的参考值，通过图表能够更加直观地观察出各参数与低保标准之间的相互趋势。

3.2 模型的缺点

模型的回归变量X1、X2、X3，其对应变量是相互影响的，线性关系不能绝对的拟合，且现实影响因素较多，难以全面统计真实数据，数据缺乏导致无法对模型进行有效验证和拟合。

4 模型的推广和改进

通过对北京市与浙江省两地之间各变量进行图表分析，能够直观地发现各地之间对低保标准的建立具有相似性。因此，各省市县之间都可采用该模型，具有较强的应用价值，且操作简便，较易获得统计数据。