光圆与非光圆绞突覆冰输电导线气动力特性分析

赵桂峰， 魏丹洋， 张 猛

(郑州大学 水利与土木工程学院，河南 郑州 450001)

0 引言

架空输电导线是一种大跨、柔性的悬索结构，极易产生风致振动，特别是覆冰导线的振动更易引起闪络、跳闸，甚至断线、倒塔等一系列事故。鉴于导线的气动力特性是研究输电线路结构风振响应的基础，已有研究对输电导线的气动力特性及其影响因素展开了较多的研究。

风洞试验方面，文献[1-5]采用风洞试验对不同分裂数、不同覆冰形状、不同风攻角、不同风速等条件下覆冰与未覆冰输电导线的气动力特性开展了研究。数值模拟方面，文献[6-8]利用不同的湍流模型对输电导线的气动力特性进行了分析，并与试验结果进行对比。

然而，上述研究均将导线简化为理想光圆截面考虑其气动力，对于实际常用的钢芯铝绞线导线因多层绞制形成的绞突截面特征考虑不足。文献[9-12]分析了导线的绞突特征对导线气动力的影响，但未对绞突导线覆冰时的情况进行研究；Zdero等[13]虽然考虑了覆冰对绞线的影响，但囿于试验条件，仅分析了覆冰厚度对导线涡脱频率的影响，对于这两种截面导线气动力特性的差异并未充分研究。

基于上述分析，本文采用Fluent软件对比分析不同风速、不同导线直径、不同覆冰厚度和不同覆冰形状对光圆与非光圆绞突导线的气动力特性的影响，意图揭示两种截面覆冰导线气动力特性的差别，为输电线路结构的精细化抗风设计提供理论依据。

1 覆冰导线气动力分析基本理论

输电导线在空气中运动时，空气作用于导线上的力可以分为升力Fl、阻力Fd和扭转力Fm。这三者可统称为三分力。为便于分析，通常将三分力转化为无量纲的系数(升力系数Cl、阻力系数Cd、扭转系数Cm)来进行计算分析。当风激励作用在输电导线上时，覆冰导线横截面的受力如图1所示。

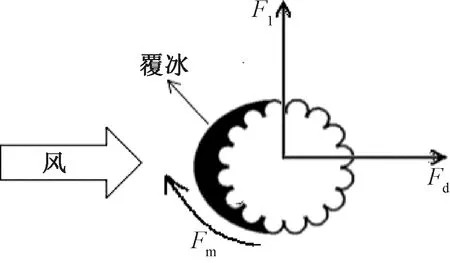
图1 覆冰输电导线的三分力Figure 1 Three component force of transmission conductor

2 导线模型的建立与验证

2.1 导线计算参数

以实际中常用的JL/G1A-400/35-48/7钢芯铝绞线[14]为例进行计算分析，根据GB/T 1179—2008《圆线同心绞架空导线》[15]，其截面排布如图2所示。

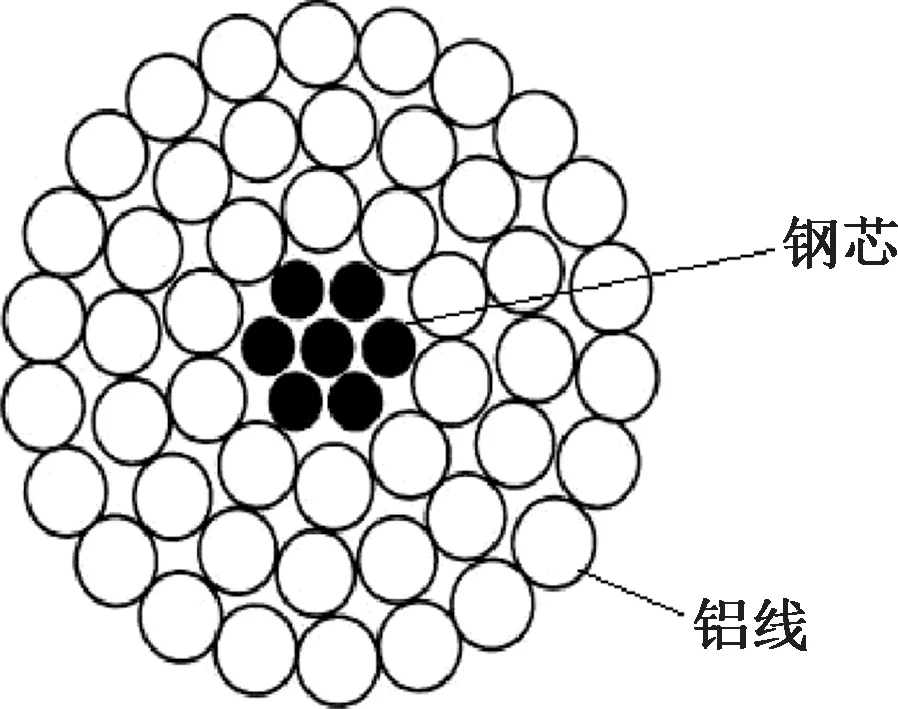
图2 钢芯铝绞线截面示意图Figure 2 Schematic diagram of steel cored aluminum strand section

2.2 模型的建立

根据文献[13，16]，利用ICEM软件建立输电导线的二维光圆和非光圆截面模型，如图3所示。

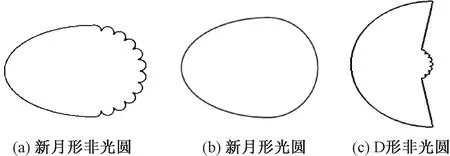
图3 输电导线截面示意图Figure 3 Schematic diagram of transmission conductor section

模拟过程中要求计算域能够保证湍流充分发展，因此设置计算域如图4所示。其中inlet为进风口，outlet为出风口，中间部分为覆冰导线，overset为网格加密区，D为导线直径。加密区采用interface连接，进风口根据相应的工况进行设置，出风口采用压力出口边界条件，总压力设置为0。湍流模型选取非直接模拟法中的SSTK-ω模型，求解采用Coupled算法。

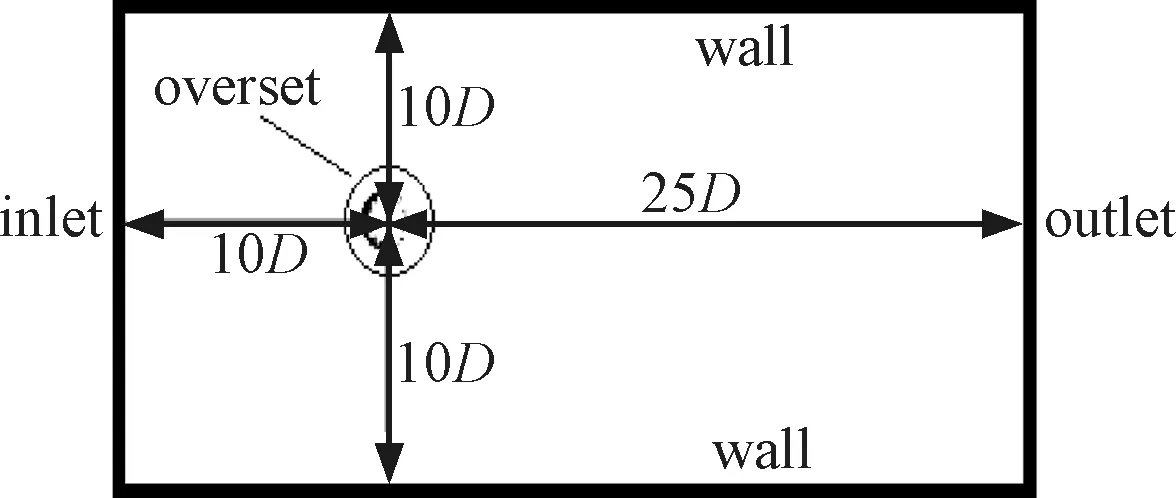
图4 数值模拟计算域Figure 4 Numerical simulation domain

在 Fluent求解计算之前，需要划分较为精确的网格以保证计算结果的准确度，本文采用网格衡量参数y+来确定较为合适的网格尺寸。对非光圆绞突截面采用混合网格，对光圆截面采用结构网格和混合网格的效果是一致的，鉴于划分网格的简便性，采用结构网格即能满足要求。而采用重叠网格的方式可以更加方便地改变风攻角。以新月形覆冰非光圆截面为例，网格划分后的示意图如图5所示。

图5 网格划分示意图Figure 5 Schematic diagram of grid division

2.3 网格无关性及模型验证

为验证本文建模和分析方法的合理性，本文采用与文献[13]相同的建模参数和工况来进行网格无关性验证，同时将本文结果与该文献的风洞试验结果进行对比。与文献[13]对应的工况：导线直径为30.5 mm，覆冰厚度为1.1D、1.4D，风攻角为0°，风速为5～20 m/s，每2.5 m/s计算一个工况。采用粗网格、中网格和细网格来进行网格无关性的验证，相关网格参数见表1，分析结果见图6。

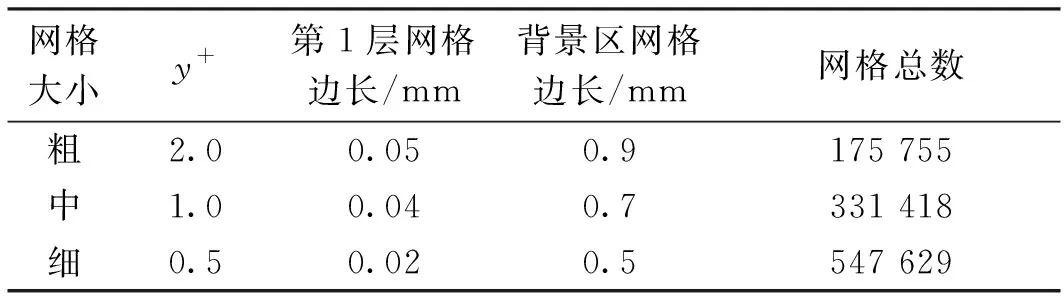
表1 网格参数Table 1 Grid parameters

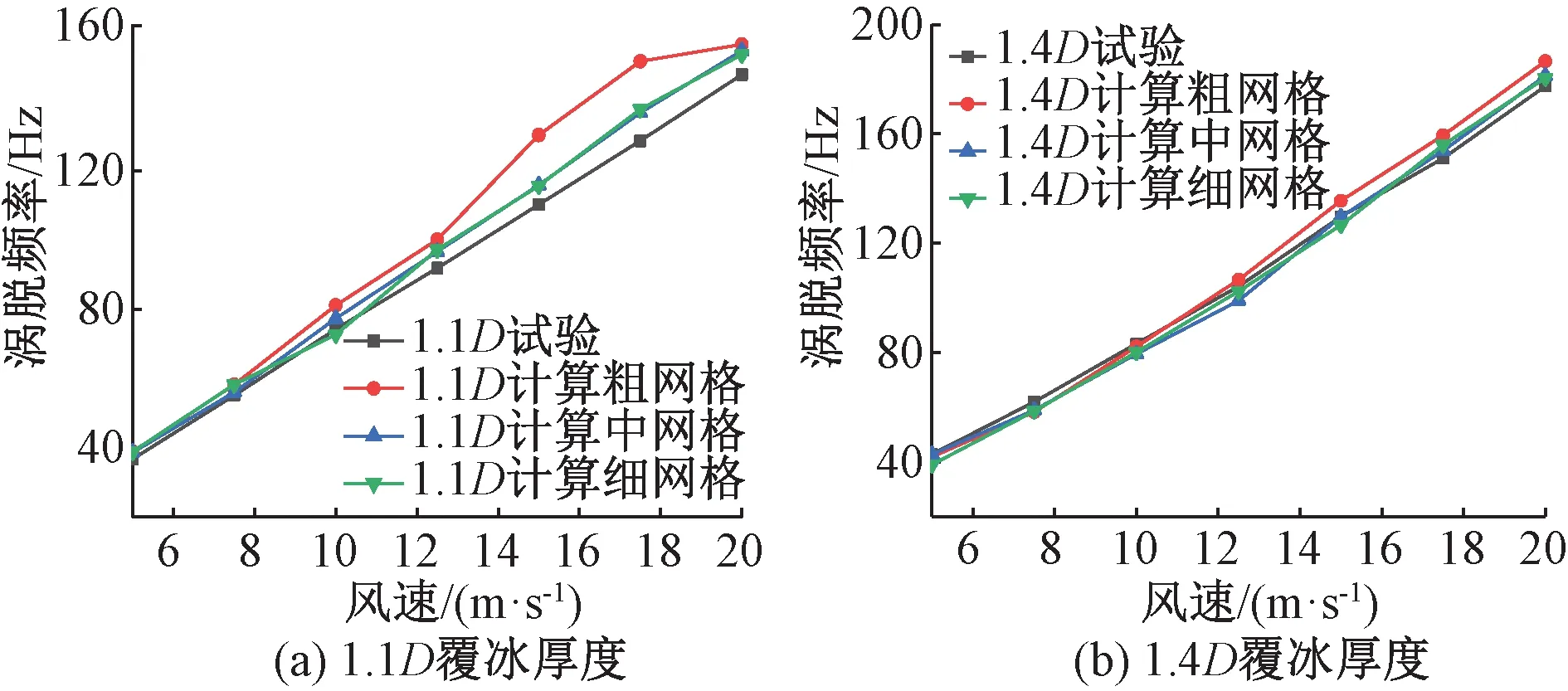
图6 不同尺寸网格下覆冰导线的涡脱频率Figure 6 Vortex shedding frequency of ice-coated conductor with different grid sizes

从图6可知，当风速不变时，同一覆冰厚度的导线在不同网格尺寸下的涡脱频率基本保持不变。对比可知，粗网格、中网格和细网格下涡脱频率最大偏差值分别为18%、6%和7%。综合考虑结果精度和机时成本，选择中网格尺寸进行计算。

3 计算结果与分析

分析不同风速、覆冰厚度、覆冰形状和导线直径对光圆与非光圆绞突截面导线的气动力特性的影响。

3.1 风速的影响

导线直径为26.8 mm，风攻角为0°～180°，冰形为新月形，覆冰厚度为20 mm，风速为5、10、15、20 m/s，两种截面导线的三分力系数如图7所示。本文中G代表光圆，F代表非光圆；相对偏差=(非光圆截面三分力系数-光圆截面三分力系数)/非光圆截面三分力系数×100%；阻力系数、升力系数、扭转系数均取其均值；X代表顺风向位移，Y代表横风向位移。

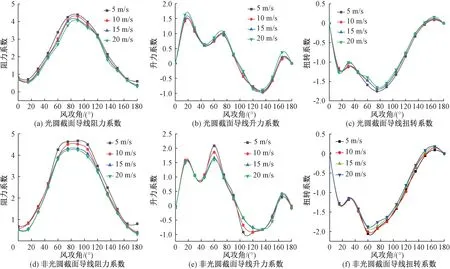
图7 不同风速下两种截面导线三分力系数对比Figure 7 Comparison of three component coefficients of two section conductors of different wind speeds

由图7可知，两种截面导线的三分力系数随风速的变化趋势基本一致，但是局部有所不同。导线表面的突起会增大导线升力系数峰值点所对应的风攻角，减小导线阻力系数和扭转系数最小值点出现所对应的风攻角。当风速不小于20 m/s、风攻角为80°～88°和178°～180°时，两种截面导线的三分力系数相对偏差均在±5%以内。在其余的风速和风攻角下，两种截面导线的三分力系数均相差较大，其中，阻力系数最大相对偏差可达-45%，升力系数最大相对偏差可达100%，扭转系数最大相对偏差可达75%。

提取两种截面导线气动力系数相对误差最大工况下的涡量云图以及顺风向、横风向位移时程曲线进行分析对比，如图8、9所示。

由图8可知，非光圆截面导线会增加周期内涡脱落的数量，由于导线的突起会导致流体分离点提前，从而产生更多的小旋涡，同时使其受力更加的不均匀，波动更加的复杂。由图9可知，非光圆截面的顺风向位移时程曲线相对于光圆截面导线波动更剧烈，其横风向位移反而相对较小并且光圆截面导线位移峰值总是早于非光圆截面出现。

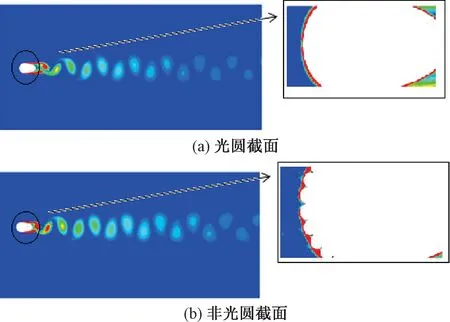
图8 风速因素下覆冰导线的涡量图Figure 8 Vorticity diagram of ice-coated conductor with wind speed factor

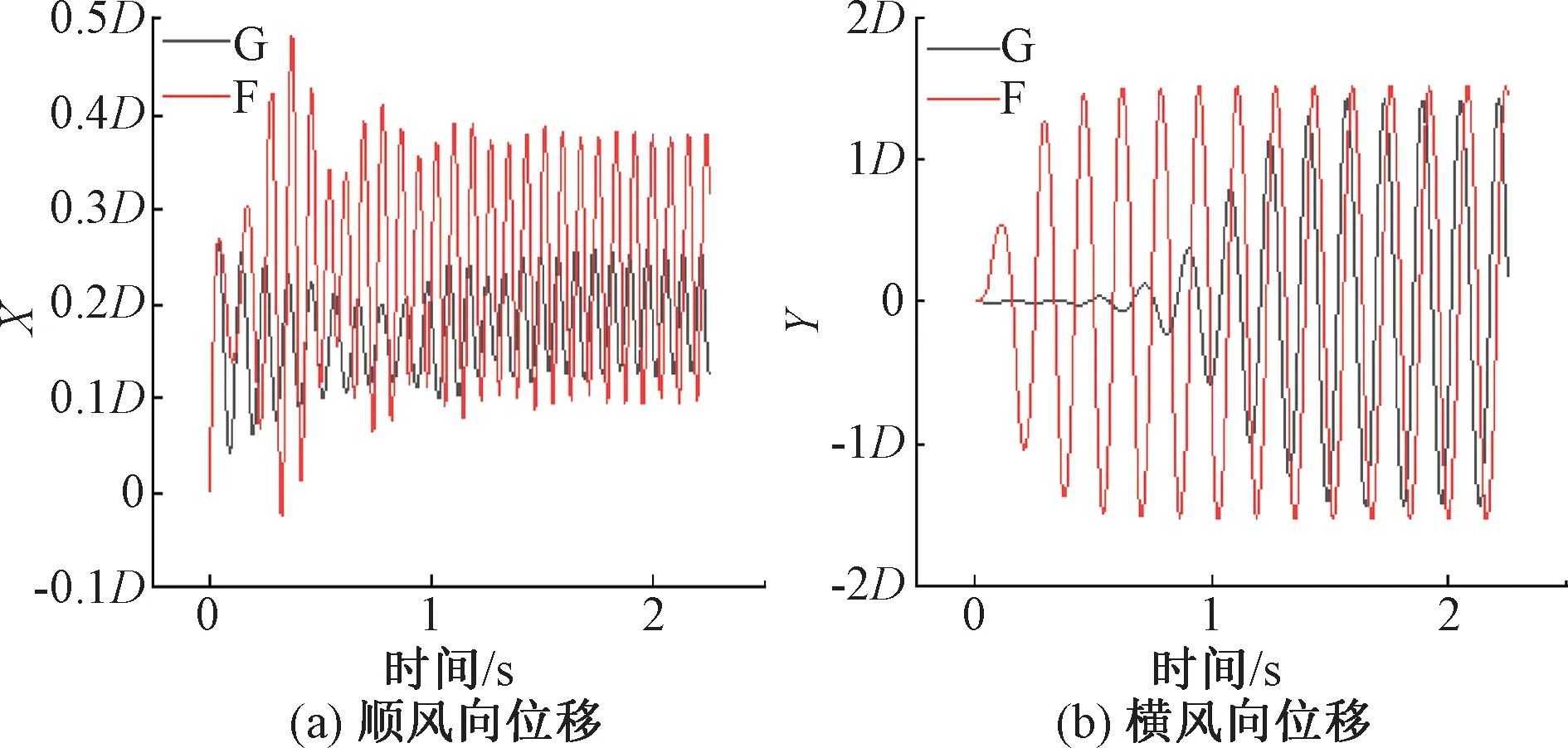
图9 风速因素下覆冰导线的位移时程图Figure 9 Displacement time history of ice-coated conductor with wind speed

3.2 覆冰厚度的影响

导线直径为26.8 mm，风速为15 m/s，风攻角为0°～180°，冰形为新月形，覆冰厚度为5～30 mm，计算结果如图10所示。

由图10可知，在风攻角为25°～165°时，非光圆截面导线的阻力系数基本上大于光圆截面导线，且其升力系数随覆冰厚度的增加更加容易产生尖峰值。当覆冰厚度为25～30 mm、风攻角为107°～122°和覆冰厚度>25 mm、风攻角为0°～5°、178°～180°时，三分力系数的相对偏差均在±5%之内。而在其他覆冰厚度和风攻角下，两种截面导线三分力系数相差较大，其中，阻力系数最大相对偏差可达-31%，升力系数最大相对偏差可达-175%，扭转系数最大相对偏差可达100%。当考虑覆冰厚度影响时，随着覆冰厚度的增加，两种截面导线的三分力系数差别逐渐增大，特别是对升力系数影响最大。

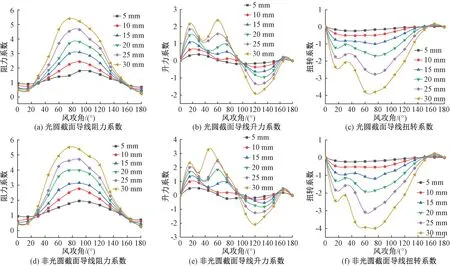
图10 不同覆冰厚度下两种截面导线三分力系数对比Figure 10 Comparison of three component coefficients of two section conductors with different icing thickness

图11给出了两种截面导线气动力相对偏差最大工况处导线的涡量云图。可以看出，非光圆导线的涡脱图波动更加剧烈，涡脱数量明显增多，说明其受力波动更大。图12为覆冰厚度因素下的位移时程图。可以看出，光圆截面导线的顺风向位移小于非光圆截面导线，而其横风向位移反而大于非光圆截面导线。

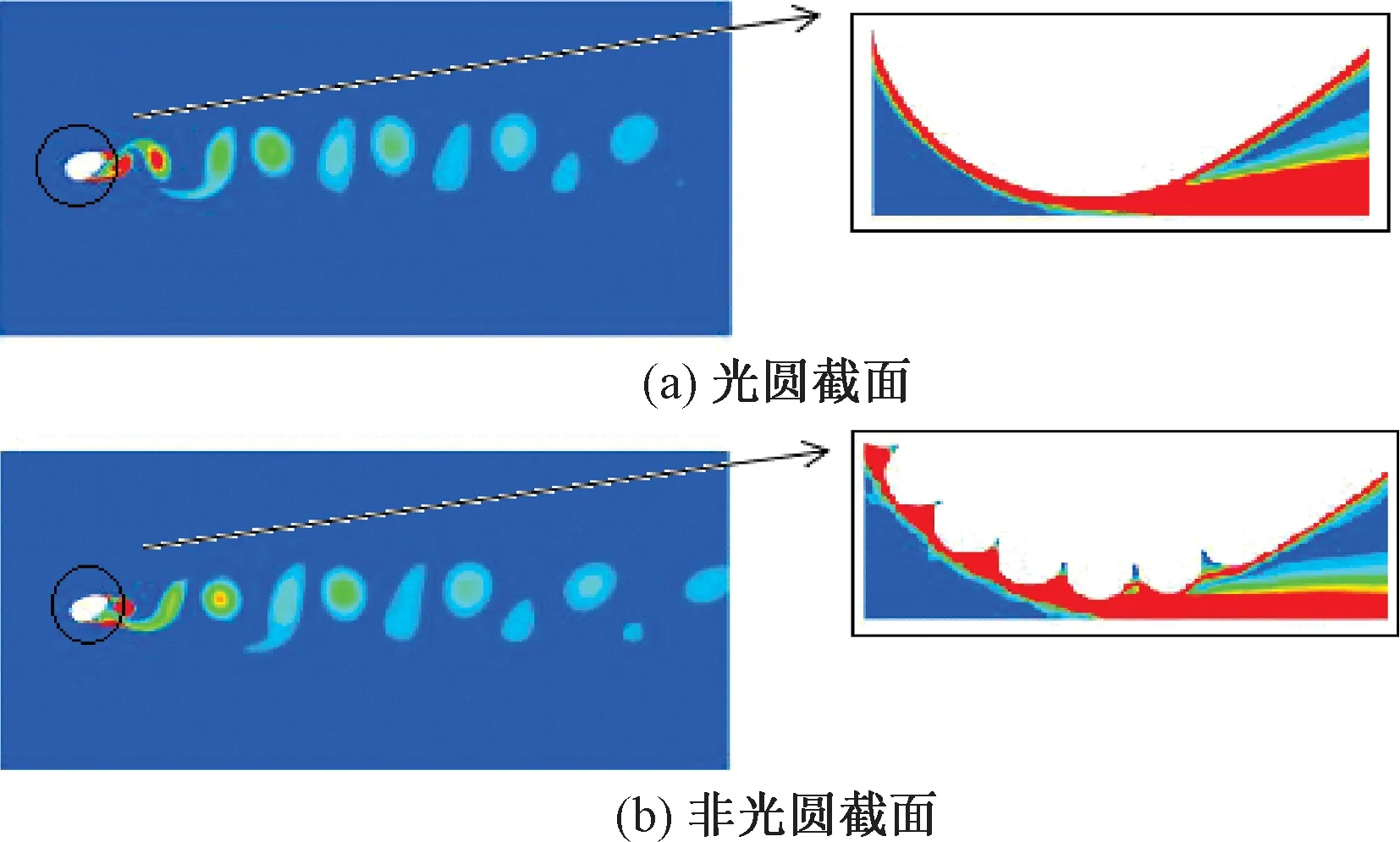
图11 覆冰厚度因素下导线的涡量图Figure 11 Vorticity diagram with of conductor icing thickness factor

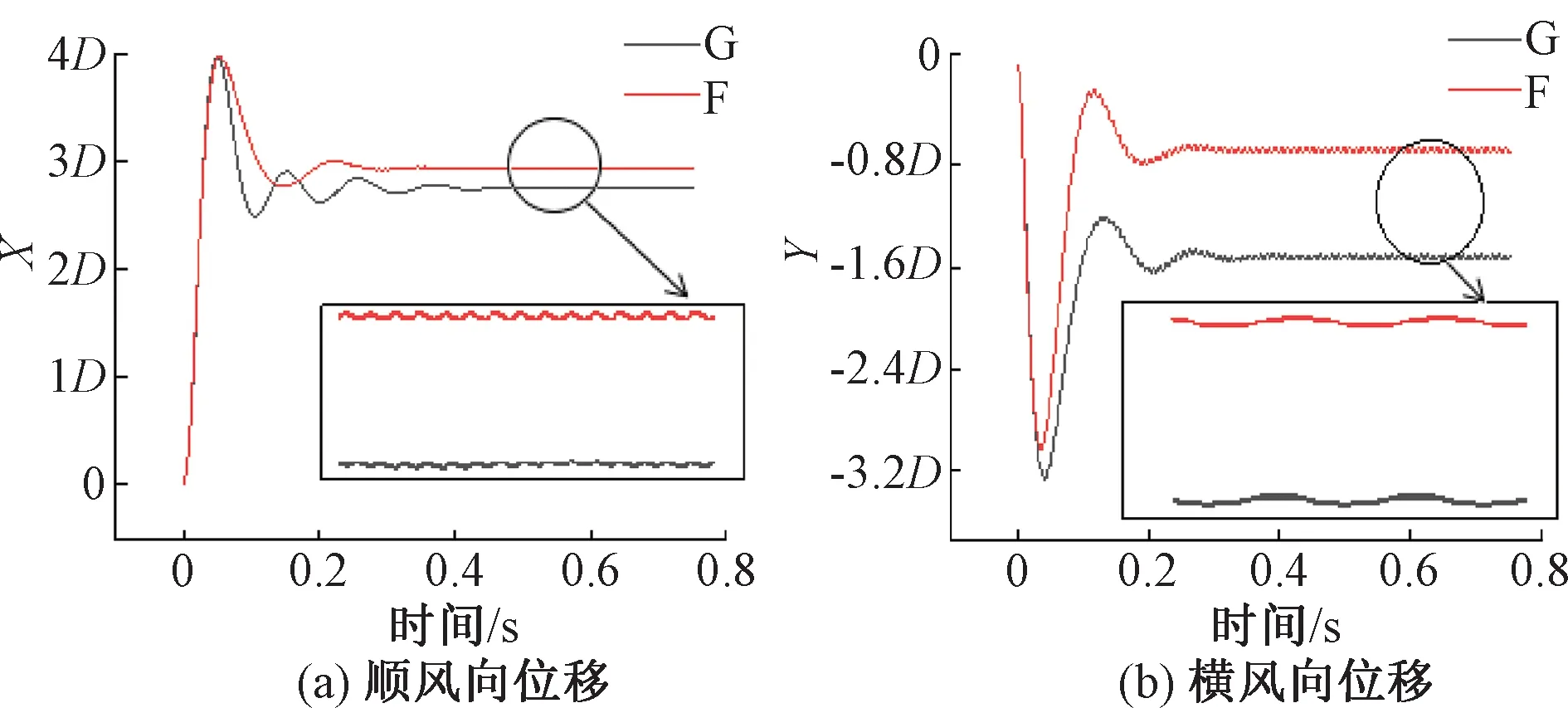
图12 覆冰厚度因素下导线的位移时程图Figure 12 Displacement time history of conductor with icing thickness factor

3.3 覆冰形状的影响

导线直径为26.8 mm，风速为15 m/s，风攻角为0°～180°，覆冰厚度为20 mm，冰形为D形和新月形，两种截面导线的三分力系数如图13所示。

从图13可知，覆冰导线在不同覆冰形状下的三分力系数有较大的不同。两种截面导线在D形覆冰下阻力系数在风攻角为0°和180°处较大，原因是其在这两处风攻角对应的迎风面较大，与新月形覆冰情况正好相反。

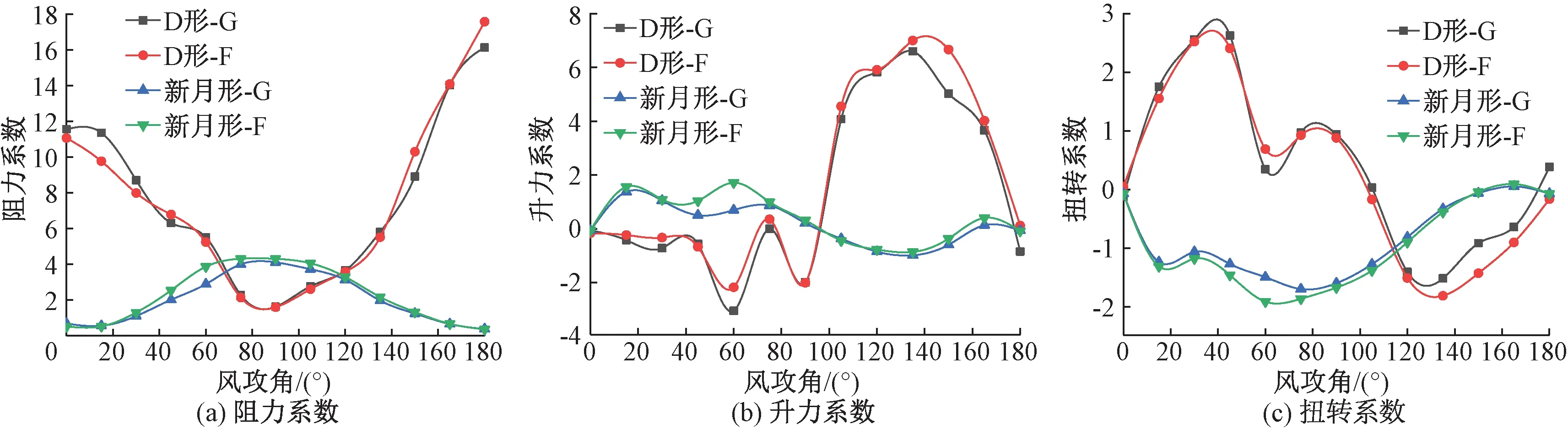
图13 不同冰形下两种截面导线三分力系数对比Figure 13 Comparison of three component coefficients of two section conductors in different ice types

D形覆冰下，非光圆截面导线的升力系数均大于光圆截面，且波动更明显，而阻力系数基本上小于光圆截面。两种截面导线在D形覆冰下的升力、扭转系数随风攻角的波动比新月形覆冰大，由此可知D形覆冰下的迎风面随风攻角的变化更大，新月形覆冰截面具有良好的流线型，气动力系数随风攻角的变化相对平滑。当覆冰形状为新月形、风攻角为156°～174°时，三分力系数的相对偏差在±5%之内。当覆冰形状为D形，风攻角为50°～55°、85°～95°、115°～134°时，三分力系数的相对偏差在±5%之内。在其他风攻角处，三分力系数相差均较大。当考虑覆冰形状影响时，不论覆冰形状为新月形还是D形，两种截面导线的三分力系数均存在较大差异，最大相对偏差达到172%。

图14、15分别为D形覆冰时三分力系数存在最大相对偏差时的涡量图和位移时程图。从图14可知，在D形覆冰下，在绞线处出现多个小涡，致使两种截面导线的涡脱的方向出现些许不同，并且增大了涡的大小。由图15可以看出，非光圆截面导线的顺风向和横风向位移波动较剧烈，光圆截面导线的顺风向位移大于非光圆截面，达到了14D，而横风向位移反而小于非光圆截面。

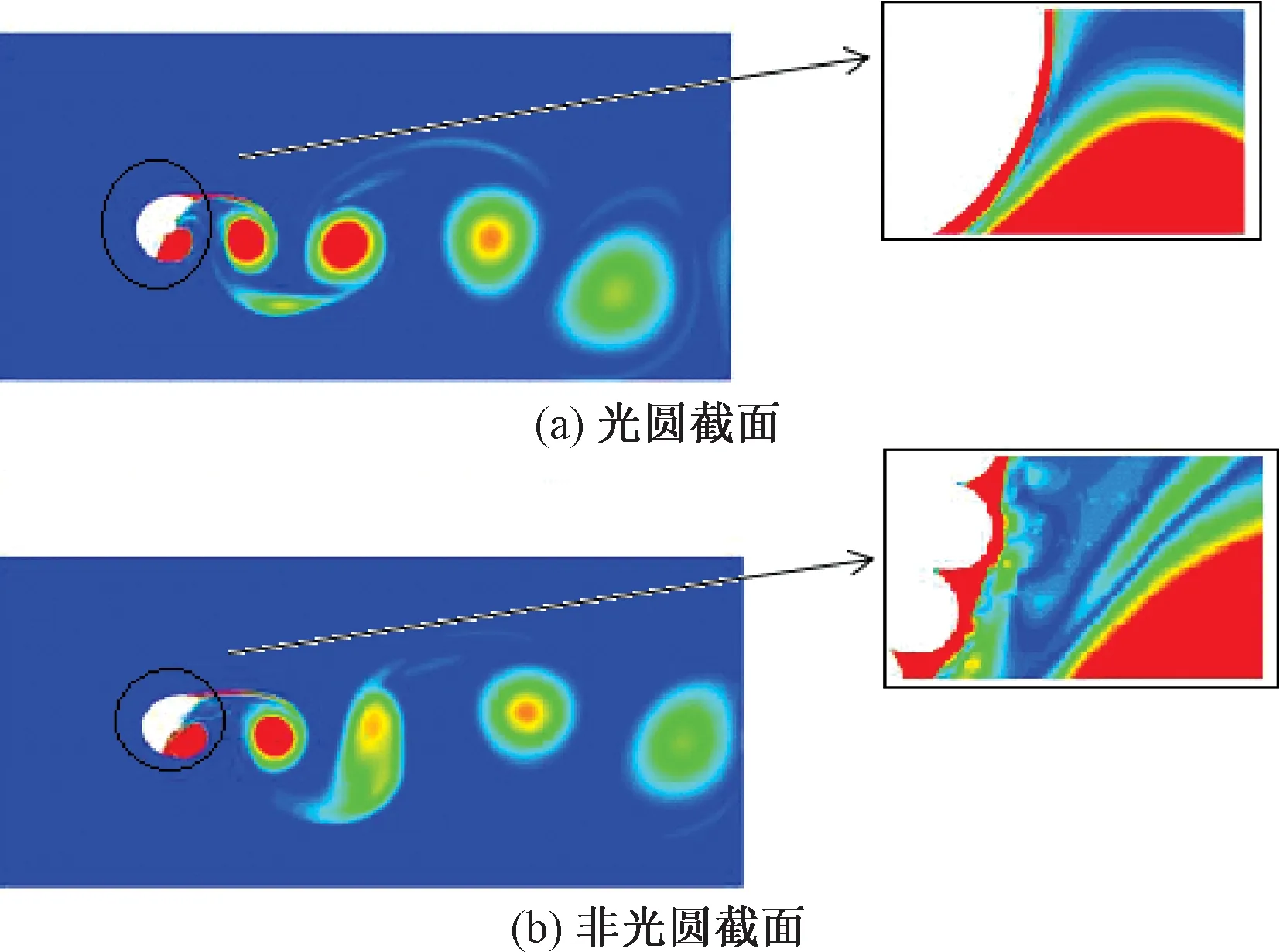
图14 D形覆冰时导线的涡量图Figure 14 Vorticity diagram of D-shaped ice-coated conductor

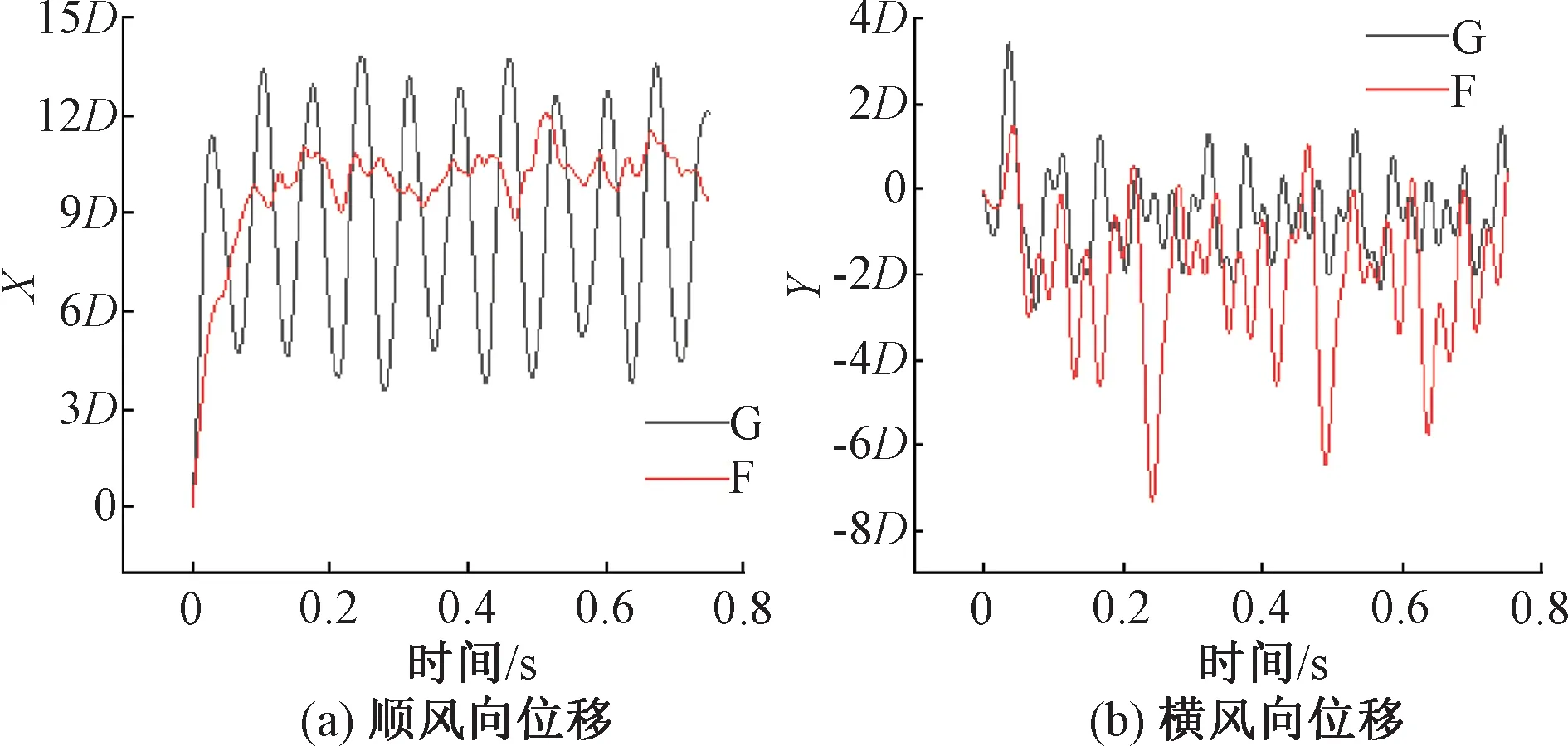
图15 D形覆冰时导线的位移时程图Figure 15 Displacement time history of D-shaped ice-coated conductor

3.4 导线直径的影响

风速为15 m/s，风攻角为0°～180°，覆冰厚度为20 mm，覆冰形状为新月形，导线直径为23.9、26.8、33.8 mm时，两种截面导线的三分力系数如图16所示。

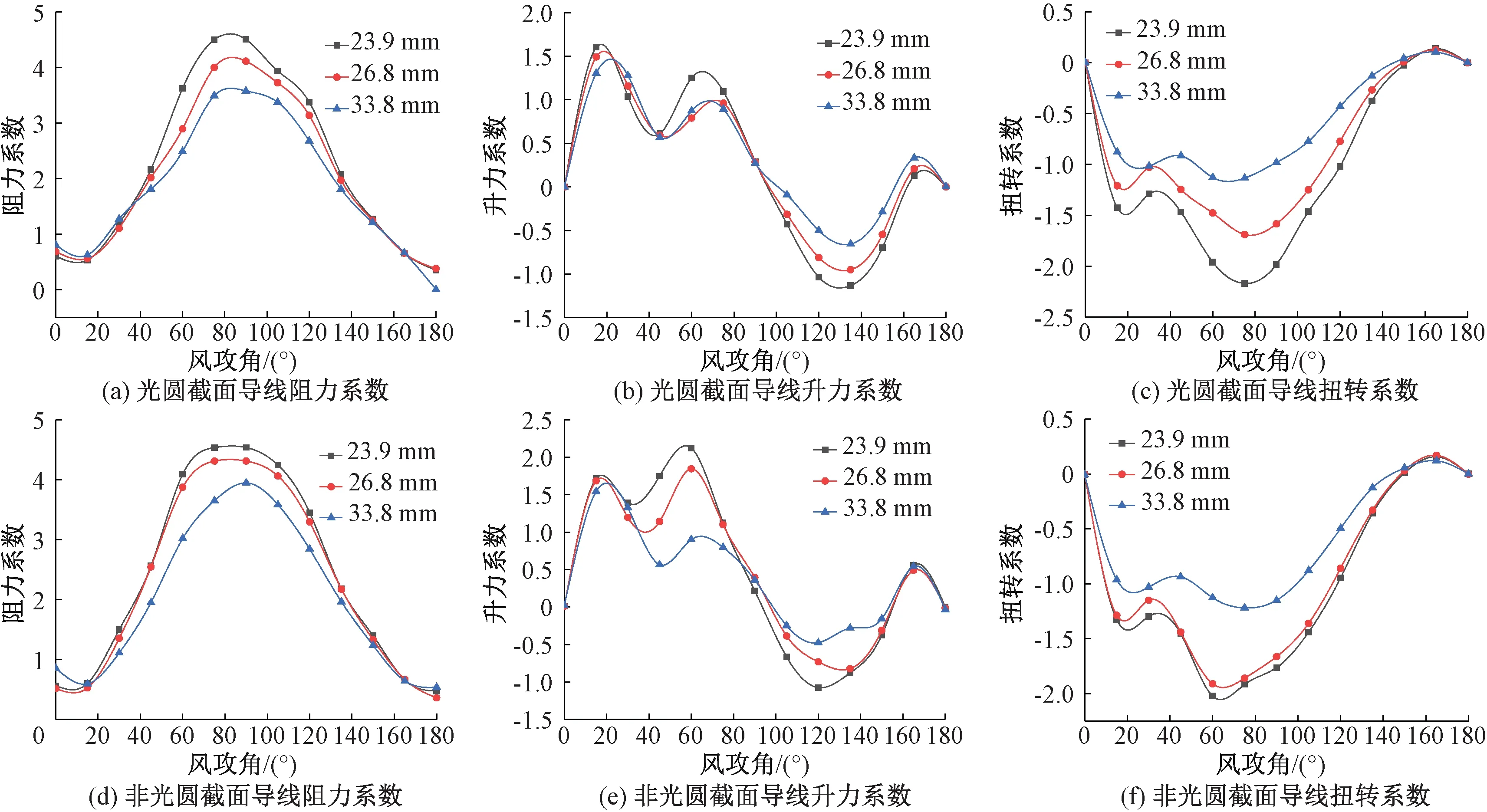
图16 不同导线直径下两种截面导线三分力系数对比Figure 16 Comparison of three component coefficients of two section conductors under different conductor diameters

由图16可知，非光圆截面导线三分力系数随着导线直径的变化波动更大，由此可知非光圆截面导线三分力系数受导线直径影响更大，不同直径导线在流场中所受气动力波动更加明显。当26.8 mm≤导线直径<33.8 mm、风攻角为175°～180°，导线直径≥33.8 mm、风攻角为38°～44°时，三分力系数的相对偏差均在±5%以内。在其他导线直径和风攻角处，三分力系数相差较大，阻力系数的最大相对偏差可达100%，升力系数的最大相对偏差可达-136%，扭转系数的最大相对偏差可达100%。随着导线直径的变化，两种截面导线的气动力系数值存在明显的不同，特别是对升力系数和扭转系数来说，非光圆截面导线升力系数的波动更大。

图17、18分别为考虑导线直径影响时三分力系数存在最大相对偏差时导线的涡量图和位移时程图。

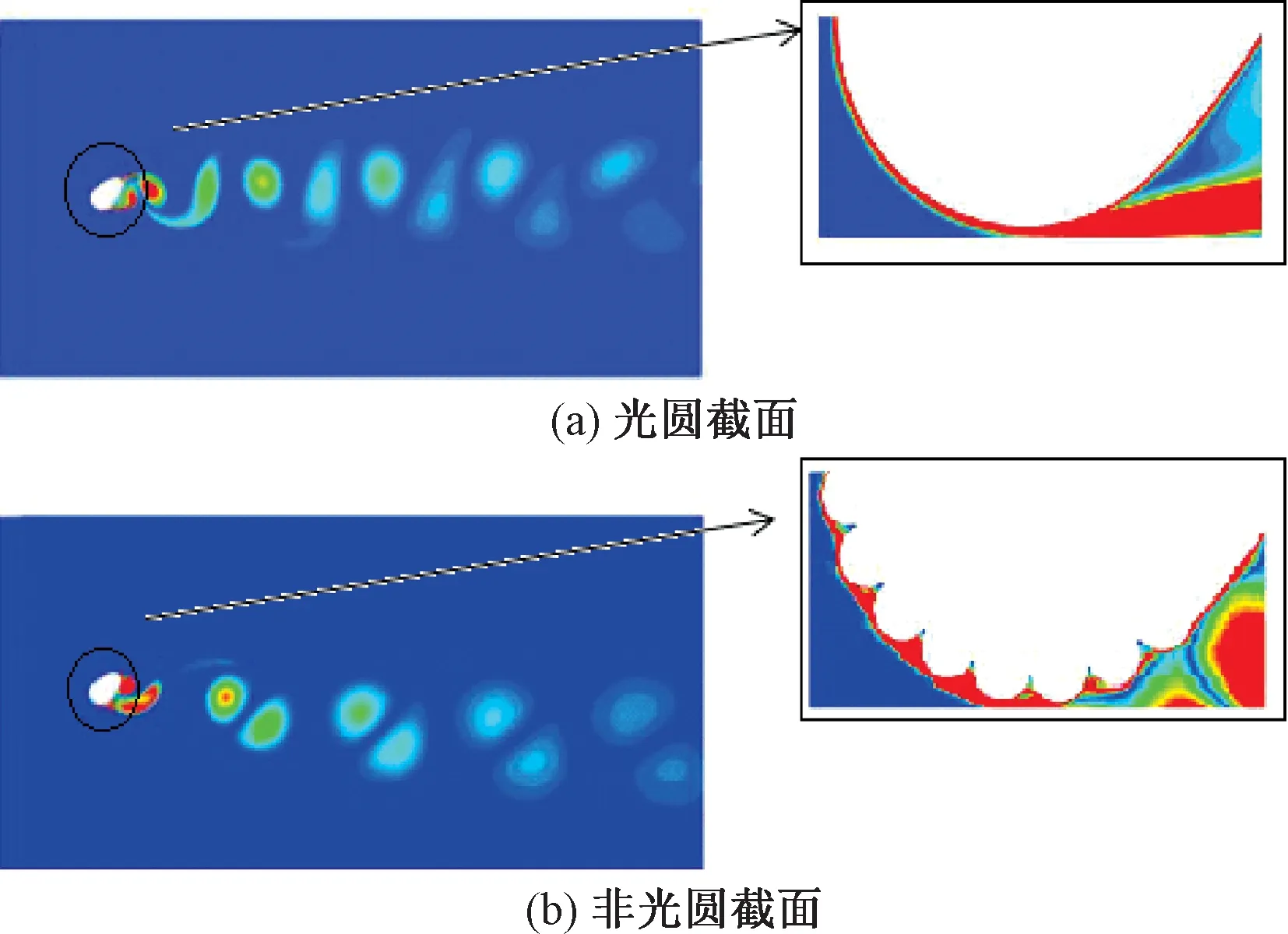
图17 考虑导线直径影响时导线的涡量图Figure 17 Vorticity diagram of conductor when considering the influence of wire diameter

由图17可知，非光圆截面导线涡结构基本呈现为2P模式，而光圆截面导线基本呈现为2S模式，非光圆截面导线的小涡明显增多。由图18可知，导线已经开始发生大幅振动，其顺风向位移最大达到7D，横风向位移最大值达到8D，仍然呈现出光圆截面的顺风向位移小于非光圆截面导线，而其横风向位移反而大于非光圆截面导线的特征。

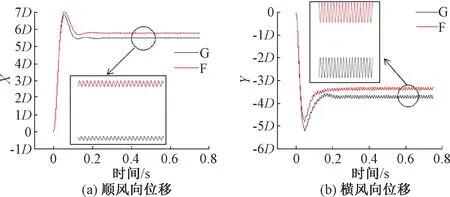
图18 考虑导线直径影响时导线的位移时程图Figure 18 Displacement time history of conductor when considering the influence of wire diameter

4 结论

(1)两种截面导线三分力系数随不同影响因素的变化趋势基本一致，但是在数值上存在较大差异，且对导线升力系数影响最大。

(2)采用非光圆截面导线会增加周期内涡脱落的数量，由于导线的突起会致使流体分离点提前从而产生更多小的旋涡，同时使其受力更加不均匀，波动更加剧烈，甚至会改变涡的结构。

(3)新月形覆冰下，采用光圆截面导线会低估导线的顺风向位移，高估横风向位移；D形覆冰下，采用光圆截面导线得到的位移时程比非光圆截面导线下的较为平缓且更有规律，会高估导线顺风向位移，低估横风向位移。

(4)两种截面覆冰导线在气动力、涡脱图和位移响应均存在较大差异，最大相对偏差可达175%。阻力系数最大相对偏差达到100%，升力系数最大相对偏差达到175%，扭转系数最大相对偏差达到100%。因此覆冰输电线路结构精细化抗风设计时应考虑到导线截面绞突特征对其气动力的影响。