基于CPU+GPU异构并行的广义共轭余差算法性能优化
黄东强, 黄建强, 贾金芳, 吴 利, 刘令斌, 王晓英
(青海大学 计算机技术与应用系,青海 西宁 810016)
0 引言
天气预报是人类农业生产、工作生活中必不可少的一部分,数值天气预报模式是目前气候预测的主要手段。中国从2001年开始自主研发GRAPES(global/regional assimilation and prediction system)数值天气预报系统[1]。
由于气象预报模式的计算量巨大,并且随着模式分辨率的提升,数值模式中积分计算量和计算耗时成倍增加。如何提高模式的计算效率是气象科研人员一直以来的研究重点。科研工作者们对数值模式并行优化的方向主要分为2种:一种是使用不同的体系架构并行,例如CPU多核并行[2]、GPU并行[3]以及国产申威异构众核并行[4-5]等;另一种是优化模式中的算法,例如采用预处理策略减少求解赫姆霍兹方程的迭代次数[6]、采用通信避免策略减少进程通信的开销[7]等。近年来,硬件架构不断升级,GPU浮点计算能力远超于CPU,因此CPU+GPU异构并行为数值模式计算提供了进一步优化的思路。
GRAPES模式中,广义共轭余差法(generalized conjugate residual method,GCR)求解赫姆霍兹方程是动力框架模块的计算核心[8]。主流的CPU并行编程方法在一定程度上为GCR求解赫姆霍兹方程提供了良好的性能[9],但是随着数值模式分辨率进一步提高,模式计算量倍增。MPI的进程通信开销限制了GCR并行的性能,为了提高GCR并行的计算效率和可拓展性,本文采用优化进程间数据通信量和非阻塞通信方式来减少进程间的通信开销。此外,稀疏矩阵向量乘法(sparse matrix-vector multiplication,SpMV)计算占了GCR算法的大部分时间。本文采用按行压缩存储(CSR)来减少SpMV计算时的访存开销,同时优化了CPU和GPU之间的数据传输量,实现CPU+GPU异构并行。
1 GRAPES中的赫姆霍兹方程
数值模式的计算效率影响着天气预报的性能,其中动力框架中的赫姆霍兹方程求解占了整个模式计算时间的1/3,因此,并行优化赫姆霍兹方程求解的计算效率尤为重要。
迭代法求解大规模线性方程组时,矩阵条件数越小迭代算法收敛效果越好。采用不完全LU分解(incomplete LU factorization,ILU)[10]对矩阵进行预处理可以通过改善矩阵条件数来减少循环迭代次数。在ILU预处理的基础上使用OpenMP、MPI、MPI+CUDA并行优化GCR来进一步提高程序的计算效率。利用OpenMP对GCR中无数据依赖的循环体进行细粒度优化;使用MPI多进程数据并行,采用非阻塞通信方式完成计算和通信的重叠,通信时只需对相邻进程间重叠区域进行数据交互;对稀疏矩阵按行压缩存储来提高访存效率,将计算密集型的矩阵计算任务移植到GPU上处理,实现CPU+GPU异构并行。
赫姆霍兹方程是由大气基本运动方程组[11]经过时间空间离散化处理后得到的,将其有限差分离散化后得
(ζΠ0)i,j,k=B1(Π)i,j,k+B2(Π)i-1,j,k+
B3(Π)i+1,j,k+B4(Π)i,j-1,k+B5(Π)i,j+1,k+
B6(Π)i+1,j+1,k+B7(Π)i+1,j-1,k+B8(Π)i-1,j-1,k+
B9(Π)i-1,j+1,k+B10(Π)i,j,k-1+B11(Π)i-1,j,k-1+
B12(Π)i+1,j,k-1+B13(Π)i,j-1,k-1+B14(Π)i,j+1,k-1+
B15(Π)i,j,k+1+B16(Π)i-1,j,k+1+B17(Π)i+1,j,k+1+
B18(Π)i,j-1,k+1+B19(Π)i,j+1,k+1。
(1)
式中:i、j、k分别表示经度、纬度以及垂直方向坐标值;其他各系数详见文献[11]。以空间下标形式展开后得到相关系数分布如图1所示[11],每个格点的计算只与其周围19个点有关(包括格点自身)。

图1 离散点相关系数分布Figure 1 Discrete point coefficient distribution
以GRAPES模式中1°数据为例,网格数据规模为360×180×38,赫姆霍兹方程未知量个数为总格点数2 462 400,方程总个数为2 462 400,其系数矩阵规模为2 462 400×2 462 400。每个方程最多有19个系数不为零,所以该系数矩阵为大型多对角稀疏矩阵。赫姆霍兹方程可简化为
Ax=b。
(2)
式中:A为赫姆霍兹方程的系数矩阵;x为解向量。求解线性方程组的方法包括迭代法和直接法,由于GRAPES模式中的方程组未知量规模与计算量过于庞大,直接法不能有效处理,因此,采用迭代法来求解赫姆霍兹方程。迭代法求解赫姆霍兹方程的算法有广义最小余差法、广义共轭余差法等。本文GRAPES模式中采用广义共轭余差法来进行求解。
2 广义共轭余差算法及优化
2.1 广义共轭余差算法
对于大规模的赫姆霍兹方程来说,其系数矩阵条件数较高,迭代收敛速度较慢,因此,对系数矩阵进行预处理以减少迭代次数。迭代法的预处理子是指构造预处理矩阵M-1使得M-1A谱分布更加集中,以此来加速迭代收敛。预处理子的构造方法有稀疏近似逆、多项式预处理、ILU分解预处理等。其中ILU分解预处理方法适用范围较广并且在求解大规模线性方程组时有较好的预处理效果[12]。
通过预处理子可以将原始线性方程组转化为易于求解的线性方程组:
A=LU-R。
(3)
如式(3)所示,ILU预处理将系数矩阵A分解成上三角矩阵U、下三角矩阵L和剩余矩阵R。计算分解因子L和U的近似稀疏矩阵L≈L-1,U≈U-1;之后以M-1=L-1U-1作为A的近似矩阵,也就是系数矩阵的预处理子。通过舍弃策略(预先决定零元素集合P,设置某些位置元素为0)保持上三角矩阵和下三角矩阵的稀疏性并且减少了计算量,同时可以加快迭代法的收敛速度。ILU预处理伪代码如下。
① Fork=1, 2,…,n-1 Do:
② Fori=k+1,k+2,…,nAnd(i,k)∉PDo:
③aik=aik/akk
④ Forj=k+1,k+2,…,nAnd(i,j)∉PDo:
⑤aij=aij/aik·akj
⑥ EndDo
⑦ EndDo
⑧ EndDo
采用ILU分解预处理矩阵,在求解过程中需要进行多次迭代计算,直至收敛到目标精度norm。GCR求解赫姆霍兹方程伪代码[13]如下。

② Doi=1,2,…,Nornorm<1E-10
③αi-1=〈Ri-1,Api-1〉/〈Api-1,Api-1〉
④xi=xi-1+αi-1Api-1
⑤Ri=Ri-1-αi-1Api-1

⑦ Doj=int[(i-1)/k]ktoi-1

⑨EndDo
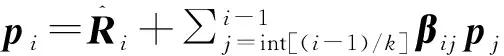
GCR求解赫姆霍兹方程的具体步骤如下:
Step 1 计算R=b-Ax的初始值以及ILU预处理子;
Step 2 进入循环迭代,当循环迭代次数超过最大迭代次数N或计算精度达到要求时,退出循环;
Step 3 计算α搜索步长,需要先进行矩阵向量乘,之后分子分母分别进行点积;
Step 4α乘以向量后与x进行向量间的加法;
Step 5α乘以向量后与R进行向量间的减法;
Step 6 ILU分解,前代回代更新R向量的值;
Step 7 根据最近的k个搜索矩阵,求β矩阵修正步长;
Step 8 通过修正步长β更新p向量的值以及Ap向量的值。
设n阶系数矩阵A每行非零元素个数为k,Krylov子空间维度为m,每次迭代中计算次数以及计算步复杂度如表1所示。其中矩阵向量乘计算占据了GCR大部分时间,因此采用CPU+GPU异构并行来提高整体计算效率。

表1 GCR中计算步复杂度Table 1 Complexity of computational step in GCR
2.2 迭代算法的比较
迭代法求解大规模线性方程组的方法有广义共轭余差法(GCR)、共轭梯度法(conjugate gradient method,CG)[14]、广义极小残余法(generalized minimal residual method,GMRES)[15]等。实验使用GRAPES模式1°分辨率数据测试不同迭代算法到达收敛精度(1E-10)时所需要的迭代次数,结果如表2所示。其中GCR、CG、GMRES未进行预处理,ILU-GCR采用ILU分解进行预处理,Jacobi-GCR采用Jacobi矩阵进行预处理。

表2 不同算法的迭代次数Table 2 Number of iterations of different algorithms
GCR算法相比于CG以及GMRES算法,其迭代次数更少。GMRES和CG算法只比GCR算法少一次矩阵向量乘操作,从整体的计算量角度来看,GCR算法更具有优势。对GCR算法进行ILU预处理和Jacobi预处理,迭代次数由134次分别减少到21、68次。可以看出,ILU预处理赫姆霍兹方程效果优于Jacobi预处理。与GCR程序相比,ILU-GCR加速比达到了3.78(加速比=原程序的计算耗时/优化后程序的计算耗时)。因此,本文基于ILU预处理的GCR算法进行CPU+GPU异构并行。
2.3 GCR性能分析
在搭载Intel Xeon Gold 6242 处理器的服务器上使用vtune对串行ILU-GCR程序进行测试分析,测试数据为GRAPES模式1°分辨率数据,结果如图2所示。

图2 ILU-GCR串行程序各个模块占比Figure 2 Proportion of ILU-GCR modules
在GCR中,稀疏矩阵向量乘SpMV是算法主要耗时模块,占了整个GCR算法时间的40%;Qsort是对CSR格式系数矩阵数据进行快速排序,以提高稀疏矩阵计算的访存效率;ILU0_M是预处理子;GetR1是ILU前代回代计算。ILU0_M和GetR1中存在数据依赖,无法很好地实现CUDA并行优化,因此,将矩阵计算部分移植到GPU上处理以充分发挥GPU的计算能力,提高程序的性能。
3 CPU+GPU异构并行优化GCR
CPU+GPU异构并行结构如图3所示。MPI启动多进程将数据划分为多个区域块,每个进程负责各自区域块上的计算,当进行迭代控制与MPI通信任务时,进程之间需要进行全局通信以及Halo区(数据重叠区域)数据交互[16]。对于计算密集型的任务(矩阵向量乘、向量点积等)采用CUDA并行,先通过PCIE(peripheral component interconnect express)将计算数据从CPU端拷贝到GPU端,在GPU端调用多个线程计算完成后,再将数据拷贝回CPU端,以此来实现CPU+GPU异构并行。
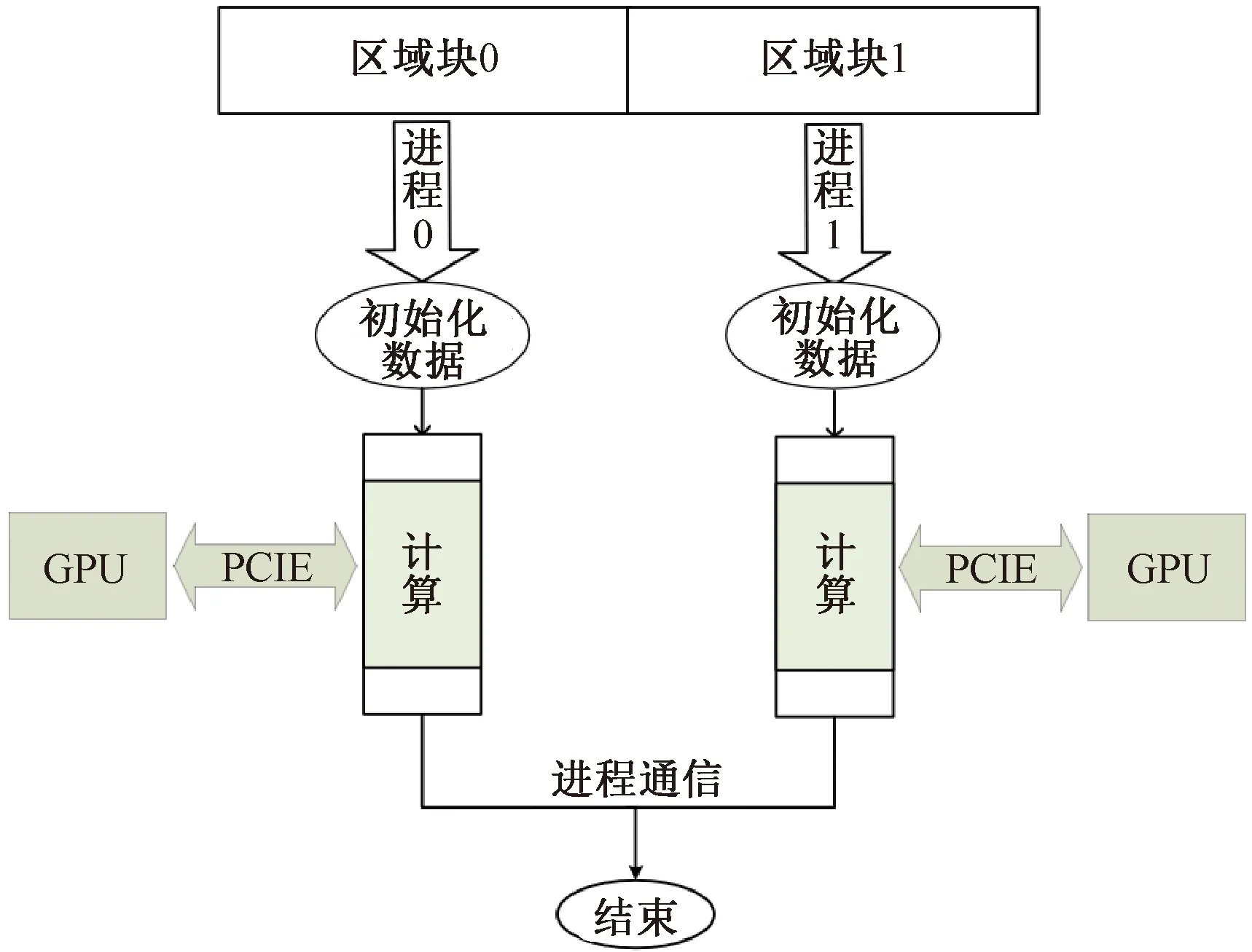
图3 CPU+GPU异构并行结构Figure 3 CPU+GPU heterogeneous parallel structure
3.1 MPI优化
3.1.1 数据并行划分区域块
通过数据并行方式优化GCR算法,根据处理器的数量对计算数据进行切分,将数据分配给各个进程进行计算,每个进程只需要对自己独占的区域块进行计算。假设MPI启动N个进程,将总数据划分为规模大致相同的N个区域块,每个进程处理其中一块区域。
MPI进程划分区域块,如图4所示,考虑左右边界情况将首进程与尾进程相连成环状,相邻的2个进程间需要进行通信。传统的数据并行方式是各进程完成计算之后进行全局数据汇总,这样各个进程间都需要进行数据交互。但是对于迭代法来说,每次迭代时进程只需计算自己所负责的区域块以及区域块的边界部分(即相邻进程之间数据重叠区域),各个进程只需对Halo区数据进行交互。这样进程间数据交互就从一对多(全局数据交互)变成一对二(相邻进程数据交互)。由此可以进一步减少节点的通信开销,提高程序的可拓展性。

图4 进程区域块示意图Figure 4 Schematic diagram of process area block
3.1.2 非阻塞通信
通过MPI_Isend和MPI_Irecv实现进程间异步通信,这使得进程在通信过程中仍然可以进行其他的计算操作。每个进程开辟了2块用于数据通信缓存的内存空间:一个是用于数据发送的空间,另一个是用于数据接收的空间。
相邻进程之间对Halo区进行数据交互。进程将数据发送到目标进程的消息缓冲区后即可继续执行下一步计算,无须等待发送和接收成功,当需要缓冲区的数据时,调用MPI_Wait函数来检测或者等待进程完成,如图5所示,由此实现计算和通信重叠,提高程序并行效率。
3.2 CUDA优化
将大规模矩阵计算移植到GPU上,主要是对GCR算法中的矩阵向量乘SpMV进行计算。CUDA优化GCR算法可分为以下3个基本步骤:
Step 1 MPI进程cudaMalloc申请所要计算的空间,cudaMemcpy将数据从CPU端复制到GPU端;
Step 2 分配线程块个数及线程数量,调用核函数在GPU上进行计算;
Step 3 cudaMemcpy将计算结果从GPU端拷贝回CPU端。
3.2.1 访存优化
对于稀疏矩阵向量乘计算,一般的二维数组格式存储稀疏矩阵所占的存储空间以及访存开销较大。因此采用CSR格式存储,可以有效提高矩阵计算效率以及减少内存空间开销,如图6所示。

图6 CSR格式存储示意图Figure 6 CSR format storage diagram
CSR存储矩阵非零元素所在的列号、元素值以及每一行的行偏移。通过行偏移ptr[i]确定第i行首元素序号,通过ptr[i+1]确定下一行首元素序号,以此确定矩阵中一行所有的非零元素,根据线程块id和线程id来划分每个线程所需计算的行,以减少矩阵向量乘的计算耗时。
3.2.2 传输量优化
在GPU上计算SpMV时都要进行CPU与GPU之间的数据传输,计算前通过cudaMemcpy将系数矩阵以及向量从CPU拷贝到GPU上,计算完成后将解向量拷贝回CPU。在GCR算法中每一次迭代时矩阵向量乘的系数矩阵不变,因此系数矩阵在GPU显存中初始化之后保持常驻。
每次进行SpMV计算时CPU与GPU之间数据传输量为ACSR_array+b+x。经过传输量优化之后除了第1次初始化SpMV,每次CPU与GPU之间数据传输量为b+x。以此进一步减少CPU与GPU之间的数据传输开销。
4 实验与结果分析
4.1 实验环境与测试用例
实验中节点操作系统为Linux Ubuntu(内核版本为4.15.0-91-generic),处理器为Intel Xeon Gold 6242 CPU,其主频为2.8 GHz,每个节点上有2块CPU(共32个核心);2块Tesla T4 GPU,显存为32 GB。实验环境中有CUDA、MPI及vtune测试工具、gcc编译器等。测试的算例是GRAPES模式1°分辨率数据(360×180×38规模的网格点),格点总数为2 462 400。
4.2 串行及OpenMP优化分析
测试ILU-GCR串行程序以及OpenMP并行ILU-GCR程序的计算耗时如图7所示。通过ILU预处理来进一步减少迭代次数,预处理后的串行程序收敛加速效果明显,ILU-GCR加速比为3.78。OpenMP并行主要是针对无数据依赖的循环体,通过调用多个线程,加速循环体的计算效率。随着OpenMP线程数的不断增加,ILU-GCR计算时间不断减少,在线程数为32时,与串行程序相比,OpenMP并行加速比达到了2.24。
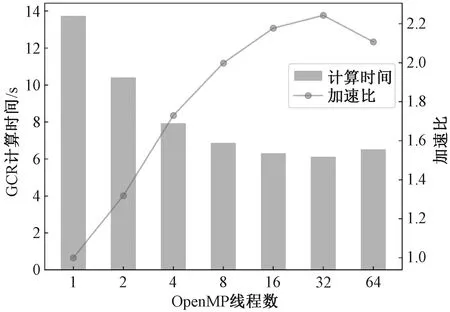
图7 不同线程下OpenMP优化ILU-GCRFigure 7 OpenMP optimized ILU-GCR in different threads
单核CPU同一时间只能处理一个线程,OpenMP并行是通过CPU调度多线程,线程过多则需要排队等待CPU执行。因此,在本实验环境中当线程数超过32之后(一个节点上只有32核),OpenMP加速效果变差。
4.3 MPI优化分析
在不同进程下,MPI优化ILU-GCR的加速比如图8所示。在进程数为16时,进程通信开销成为MPI并行的性能瓶颈。随着进程数的增多,通信开销逐渐大于计算开销,导致程序的可拓展性较差。本文对进程通信数据量进行优化以及采用非阻塞通信方式优化之后,随着进程数的增加,ILU-GCR计算时间呈线性递减,提高了程序的可拓展性和计算效率。

图8 不同进程下MPI优化ILU-GCRFigure 8 MPI optimized ILU-GCR in different processes
MPI粗粒度并行比OpenMP细粒度优化效果更好,它从程序初始化阶段就已进入了并行模式,各个进程共同执行程序并各自计算所负责的区域块。与串行程序相比,4进程下并行ILU-GCR的加速比为3.32,64进程下并行ILU-GCR的加速比为34.01。
4.4 CPU+GPU并行分析
实验将ILU-GCR算法中的大规模矩阵计算部分移植到GPU上,通过CPU进程调用GPU上的kernel计算函数来完成MPI+CUDA混合并行,采用压缩矩阵行方式来减少计算量以及提高访存效率。将系数矩阵常驻在GPU显存中来减少迭代过程中CPU和GPU之间的数据传输量。
CPU-GPU异构并行ILU-GCR算法后,在进程数为4时,MPI+CUDA并行ILU-GCR加速比相较于MPI并行ILU-GCR为1.41,相较于串行程序为4.69。
5 结论
本文使用CPU和GPU上的3种并行编程方式(OpenMP、MPI、CUDA)并行优化GRAPES模式中的计算核心GCR,以求解赫姆霍兹方程。采用不完全LU分解预处理减少迭代次数,在此基础上,使用OpenMP结合共享内存细粒度并行ILU-GCR算法;在MPI并行中采用非阻塞通信和优化进程通信量的方式使ILU-GCR程序性能有良好的可拓展性,随着进程数的增多,GCR的计算时间呈线性减少;通过访存优化和CPU/GPU间数据传输量优化使MPI+CUDA异构并行ILU-GCR的计算效率进一步提高。实验结果表明:在Intel Xeon Gold 6242 CPU、Tesla T4 GPU的平台上与ILU-GCR串行程序相比,OpenMP、MPI以及MPI+CUDA异构并行ILU-GCR的加速比分别达到了2.24、3.32、4.69。

