基于非线性动力学的2H桥级联式三电平单相逆变器的稳定性分析

陈庆花，李学武

(郑州铁路职业技术学院，河南 郑州 451460)

多电平逆变器在提高电力系统的控制能力、治理电力系统的谐波污染、提高交流电动机传动系统的节能效果和性能上有着重要的作用[1-3]。但是，由于多电平逆变器系统中存在很多开关器件，在其工作过程中，这些开关器件会快速通断，因此就会出现一些诸如分岔、混沌等非线性现象，严重影响了逆变器系统的稳定性。本文以2H桥级联式三电平联式逆变器为研究对象，利用非线性动力学分析方法对其稳定性进行研究。

1 建立2H桥级联式三电平单相逆变器数学模型

2H桥级联式逆变器的工作原理如图1所示，逆变器开关管为理想开关管，两个2H桥串联。以参考电流iref和负载电流iL作比较，通过比例环节得到调制信号ucon，与两个双极性三角波进行比较，进行CPS-SPWM控制。

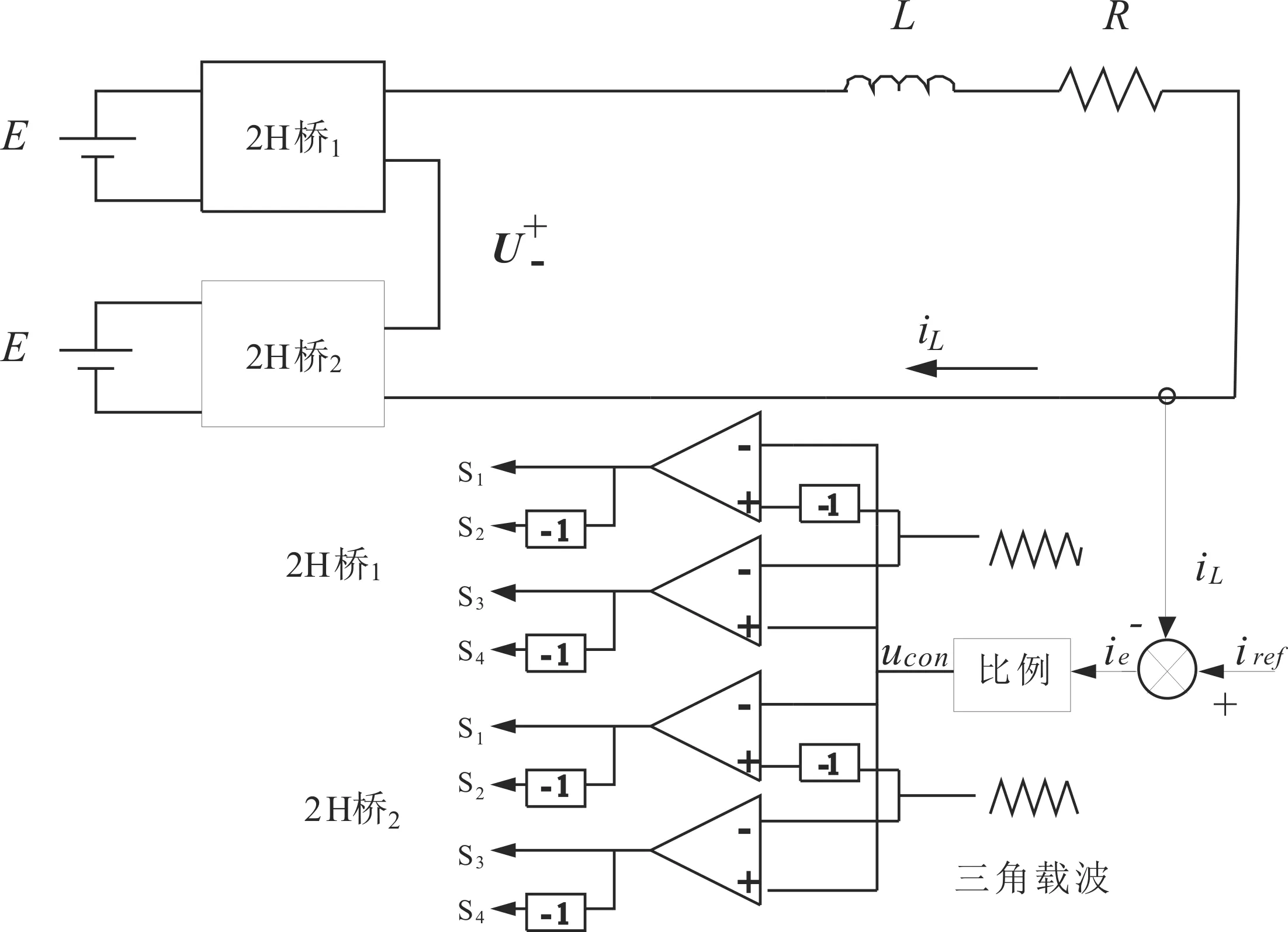
图1 2H桥级联式逆变器的工作原理

利用频闪映射方法对2H桥级联式逆变器建立数学模型，化简可得：

(1)

式(1)中，Ts为开关频率。

2 系统分岔图和折叠图分析

对于系统中有非线性现象的开关电路，可以利用分岔图和折叠图直观看出系统处于稳定状态还是不稳定状态。选取逆变器参数E=200 V，R=30 Ω，L=20 mH，iref=10 sin(100πt) A，Ts=100 μs，开关频率fs=10 kHz，电压电流频率为f=50 Hz。

2.1 分岔图

利用Matlab对公式(1)进行处理编程得到系统分岔图，如图2所示。

图2 系统分岔图

此分岔图以比例系数K为分岔参数，通过迭代运算，选取输出电流稳定后的若干个正弦波峰值进行采样。由图2可以看出，系统电流采样点在K∈[0.4,1]时重合为一点、在K∈[1.01,1.1]时分岔为两点，说明系统在K=1.01时发生倍周期分岔；在K>1.1时采样点杂乱无章，此时系统处于混沌状态。以上分岔状态和混沌状态都为不稳定状态。

2.2 折叠图

利用Matlab对公式(1)进行编程处理可得系统折叠，如图3所示。

(a) (b)

折叠图为系统迭代运算后，将稳定后的若干个采样周期所有采样点折叠在一起形成。图3(a)为K=1时系统输出电流的折叠图，由图可以看出此时系统处于单周期稳定状态。图3(b)为K=1.01时系统输出电流的折叠图，由图可以看出此时系统处于倍周期分岔状态，和分岔图分析结果保持一致。

3 系统雅可比矩阵分析

系统雅可比矩阵可由式(1)确定。

(2)

将式(2)在Matlab中进行处理可得系统雅可比矩阵特征值随K值变化的轨迹，如图4所示。

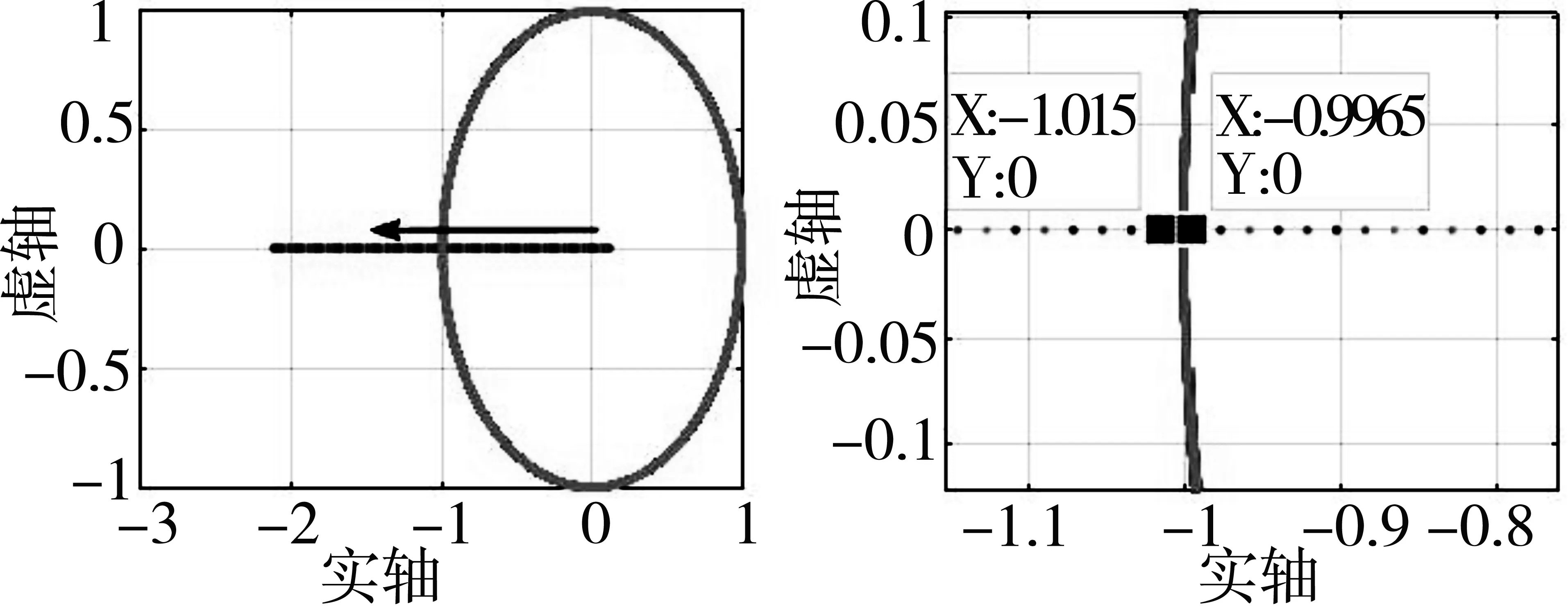
(a) (b)

由雅可比矩阵特征值轨迹可以判定系统的稳定性：当特征值轨迹位于单位圆内时，系统处于稳定状态；当特征值轨迹位于单位圆外时，系统处于不稳定状态；当K=1.01时，特征值轨迹从内而外穿越单位圆，此时系统处于倍周期分岔状态，与之前的结论保持一致。

4 系统的稳定性分析

由雅可比矩阵特征值轨迹可知：当最大特征值的模小于1时，系统处于稳定状态；当最大特征值的模大于1时，系统处于不稳定状态。由此可以得到系统最大特征值模随K值变化的曲线，如图5所示。

图5 最大特征值模随K值变化的曲线

根据雅可比矩阵最大特征值模的变化，可以得出任意两个系统参数变化时的稳定区域。选取电压E和比例系数K同时变化时的系统稳定区域和不稳定区域，如图6所示。

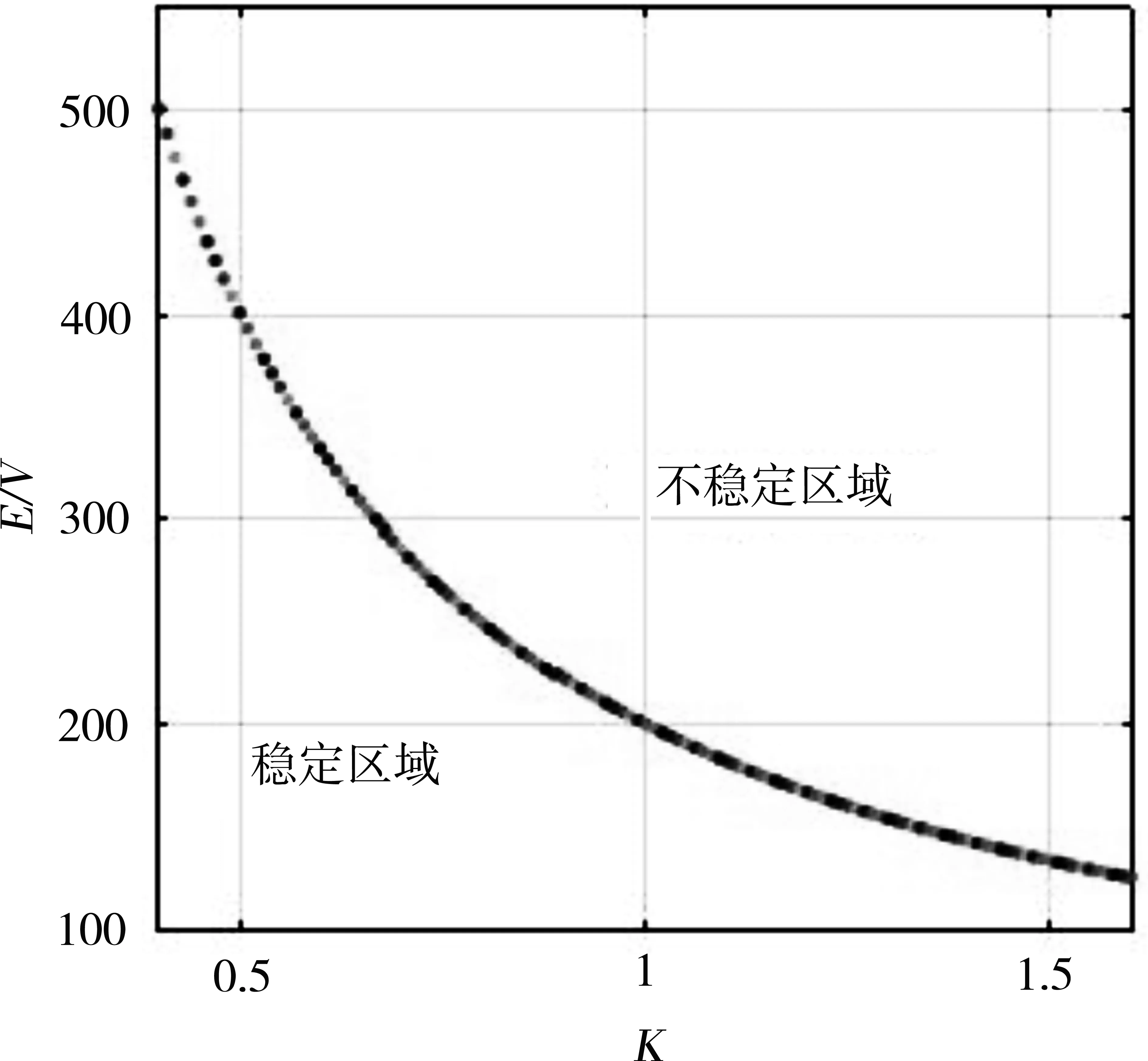
图6 系统稳定区域分布

5 结语

以2H桥级联式三电平逆变器为研究对象，针对逆变器在运行过程中出现的不稳定现象，利用非线性方法对其进行稳定性分析，得到了系统的稳定范围，为逆变器设备的设计和调试提供了指导和借鉴。