基于FPGA的高斯噪声数字调频算法研究与实现

刘富星，孙逸洁，任全会

(郑州铁路职业技术学院，河南 郑州 451460)

随着电子信息技术的快速发展，电子干扰在现代战争中应用越来越广泛，其主要应用在雷达、军用GPS系统中。噪声调频信号因其具有宽干扰带宽和大噪声功率的特点而被作为最重要的干扰信号。在实际应用中，对噪声调频信号发射系统要求很高，要求此信号的带宽较宽，同时还要求其中心频率和带宽控制的精度也要高[1]。

以往产生噪声调频信号的常用方式有简单模拟或半数字化，这类方式存在稳定性差、控制精度不高、受外环境影响大、不能进行实时处理的缺点，所以在应用中受到了很大的限制[2]。随着FPGA(可编程门阵列)的广泛使用，基于FPGA的高斯噪声数字调频算法可有效解决以上问题。此算法中噪声调频信号主要通过DDS软核产生并在FPGA上实现，通过此系统产生的噪声调频信号具有可在线升级、实时处理、全数字化的优点。通过系统仿真和硬件电路测试，验证了系统的可行性。

1 数字化噪声调频信号产生原理

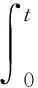
(1)

式(1)中，A0是幅度，Kf是调频指数，φ0是载波相位，ν(t)是零均值的广义平稳随机过程[3]。

ν(t)的概率密度函数可表示为：

(2)

式(2)中δν是噪声方差均方根值。

经过ν(t)调制载波信号后，噪声调频信号瞬时角频率和功率谱QN(ω)可分别表示为：

ω(t)=ωc+Kfν(t)

(3)

(4)

设有效频率为ωd，瞬时频偏为△ω，即有Kfδν=ωd，△ω=ω-ωc，则噪声调频信号实际功率谱可表示为：

根据设计的3组试验，可得到试验结果见图3～图5。图3～图5中曲线显示的是船舶减速概率随船舶减速影响参数的变化关系，横坐标表示不同的船舶减速影响参数，纵坐标为船舶减速概率。仿真试验结果采用2种方案统计:一条曲线统计在整个仿真时间内所有发生减速的船舶数目与总船舶数目的比值，该曲线反映的是在试验条件下航道内的船舶减速状况；另一条曲线在统计结果时不计入因船舶减速连锁效应影响下的减速船舶，该曲线用来验证船舶减速概率模型的精度。从图3～图5中可知:3艘船舶减速影响因子与船舶减速概率相关性较好，其取值的增加都会使航道内发生减速的船舶比例增大。

(5)

式(5)中，P0是实际总功率，P0=1/2Am2。噪声调频信号的半功率频谱带宽是：

Δω0.5=2.35ωd=2.35Kfδν

(6)

当给定调频指数Kf和噪声方差均方根δν两个参数其中一个时，另一参数也可求出，同时还能保证所需的半功率频谱带宽。

2 系统硬件总体设计

系统硬件总体框图如图1所示，主要包括电源配置电路模块、时钟分配模块、DAC模块和FPGA模块，其中FPGA模块是系统的核心控制模块，通过QuartusⅡ对FPGA芯片进行开发。选用Altera公司的StratixIV型FPGA，该芯片具有90960个LE单元，RAM为4520488 bit，DSP乘法器模块384个，完全能够满足噪声调频信号产生需要的资源[4]。

电源配置模块主要给FPGA芯片提供3.3 V和5 V电压，其通过开关电源芯片和线性电源芯片等实现；时钟分配模块主要给FPGA、DAC、PCI9054提供稳定的时钟信号；DAC模块把FPGA产生的数字噪声调频信号转换为模拟信号，转换后的信号中心频率和带宽都是可调的，其频率区间为1～350 MHz。

3 系统结构设计

设X1，X2，X3，…，Xk为相互独立的正态随机变量，同时满足N(μk，δk)分布，即：

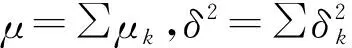
(7)

满足正态分布的高斯随机变量可以使用Wallace算法利用式(7)产生。把满足单位正态分布的N个源变量进行实现平方和为1的归一化处理，设Y=AX(A为正交矩阵)是正交变换，把K个变量当作一个向量X，这样就可以得到一个同样满足正态分布的K维向量Y，通过平方和对得到N个新变量进行修正，同时使用缩放因子G使经过修正的变量服从x2分布,这样基本满足标准正态分布的高斯采样值就可以实现了[5]。具体的系统结构图如图2所示，其中实线和虚线分别代表数据信号和控制信号。

图2 系统结构图

3.1 均匀随机信号发生

使用有利于快速实现均匀伪随机序列的Tausworthe算法。具体的结构图如图3所示。

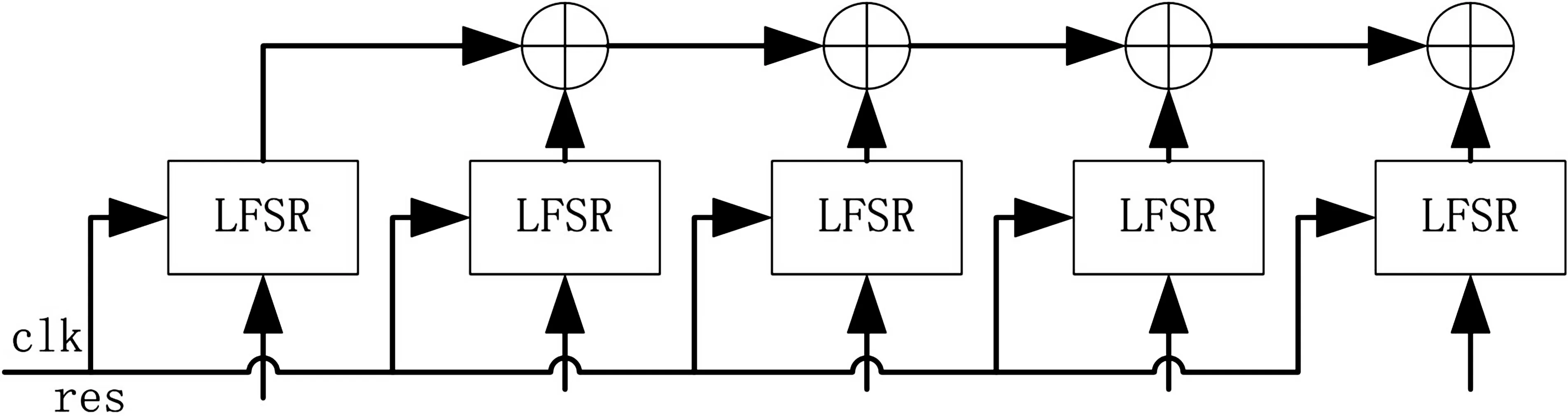
图3 均匀随机信号发生单元硬件结构图

N个随机数的产生可以通过N个M位LFSR(线性反馈移位寄存器)实现，然后通过异或运算就可以得到周期为2M同时满足均匀分布的伪随机序列。系统使用5个周期是232的均匀分布随机序列，设u=s1⨁s2⨁s3⨁s4⨁s5为均匀随机变量，s1、s2、s3、s4、s5的初始值为2、4、8、16、32。Si(i=1,2,3,4)可表示为：

si=((si&mi<>wi)

(8)

式(8)中，mi，ni，ki，wi是常数，这些常数都能通过Tausworthe算法计算得到。

3.2 地址产生模块

此模块主要完成对输入均匀随机变量进行正交变换，同时输出p、q、r、s四个长度是n2的独立地址。这样不但提供了变换前的读地址，同时也提供了变换后的写地址。设地址长度为10 bit，具体算法为：

(9)

式(9)中，u是均匀随机变量。

3.3 正交变换模块

通过归一化高斯变量生成模块之后的变量是标准的归一化高斯随机变量。正交变换模块主要作用是尽量减少此变量和变换前源变量之间的关联。1024个归一化高斯随机变量被存在ROM(只读存储器)上，均匀随机地址在系统运行时会对双口RAM(随机存取存储器)进行读写，这样就可以完成两个归一化随机变量的输出。随机数X通过正交变换模块可以得到Y(Y=AiX，i=1，2，3，4)，正交变换矩阵A1、A2、A3、A4在计算时是依次使用的[6]。具体可表示为：

(10)

正交变换模块的运算速度较快，因为通过FPGA实现四矩阵乘法很容易，仅需要7次加法和1次移位运算即可。

3.4 平方和修正模块及噪声调频DDS模块

平方和修正使用Wallace算法，通过此过程即可得到指定均值和方差的高斯白噪声。把N(单元具体实现时N=1024)个随机数乘修正值G进行平方和修正。

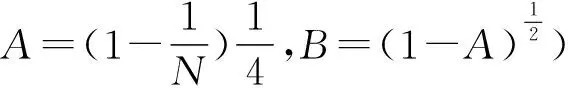
(11)

式(11)中G的平方和满足x2分布。

DDS主要通过采样计算实现频率可调的正弦信号，硬件结构原理图如图4所示。

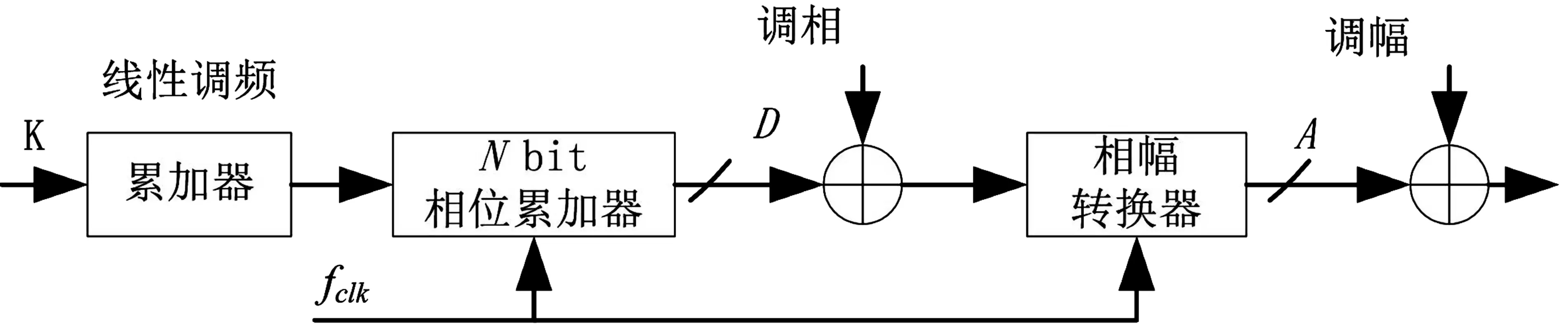
图4 DDS硬件结构原理图

其中K是频率控制字，N是字长，fclk=100 MHz。N为38位时，频率分辨率为0.18×10-6Hz，这样可以使运行速度与频率分辨率达到均衡状态[7]。

3.5 均值与方差控制模块

此系统中δν=1，该模块接收到的可配置参数有Kf、A0、ωc，通过参数Kf可设置噪声调频信号的带宽、通过参数A0可设置频谱的中心位置、通过参数ωc可设置输出功率、经过设置合理的参数可以得到所需参数的噪声调频信号。

4 测试结果和结论

4.1 测试结果

系统通过Modelsim软件得到1×105个随机变量，通过MATLAB对这些序列进行分析，分析结果如图5所示。同时对均值和方差两个参数进行计算，均值为0.0016、方差为1.001，基本等于归一化高斯噪声理论值。

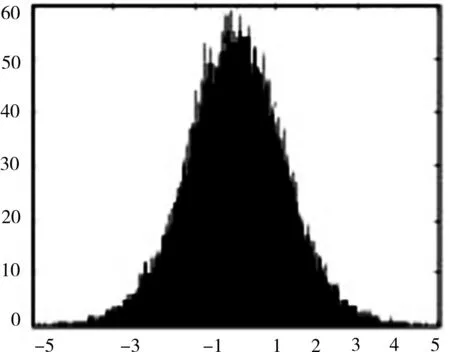
图5 高斯序列分布直方图

通过频谱分析仪对此信号进行测试，这样能证明此系统输出的噪声调频信号是否符合预期，具体的测试结果如图6所示。

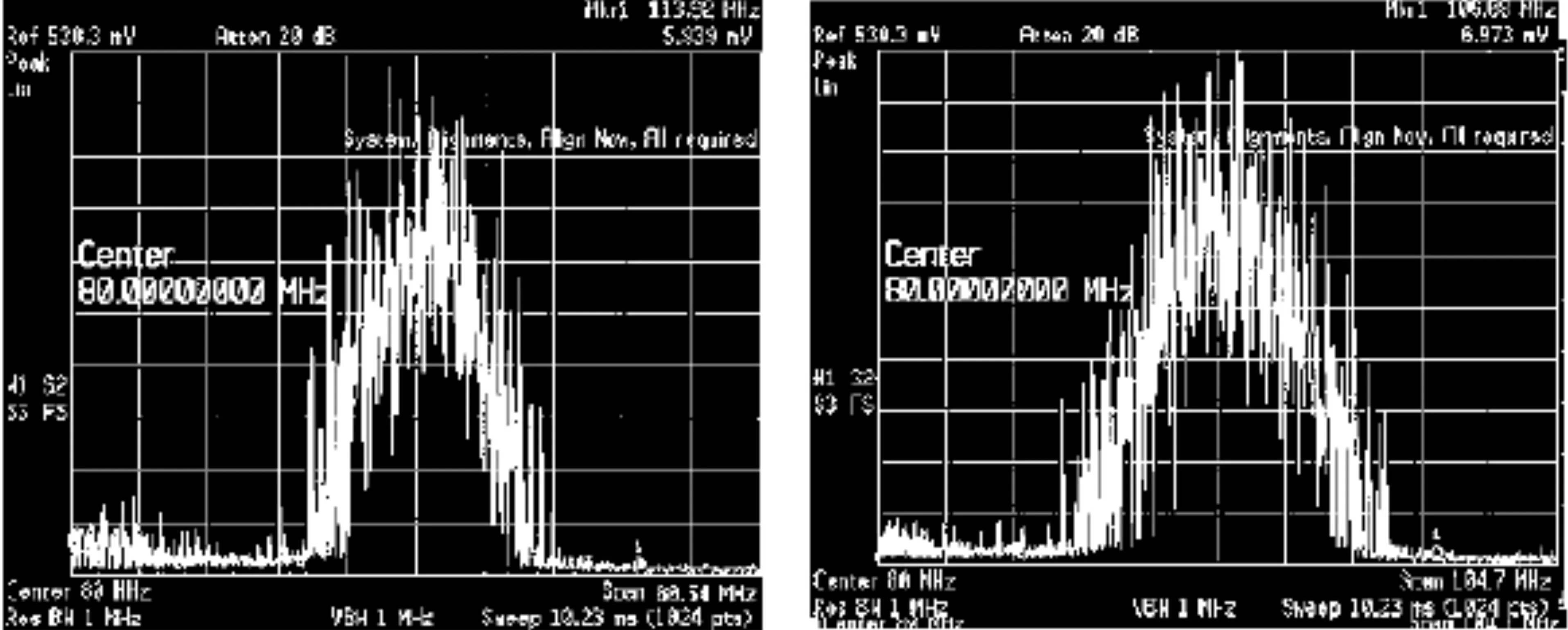
(a)Δω0.5=40.27 MHz (b)Δω0.5=52.35 MHz

图6(a)中，Kf=16.138×106、A0=1、ωc=80×106，带宽为80.54 MHz,图6(b)中Kf=22.369×106、A0=1、ωc=80×106，带宽为104.7 MHz。

4.2 结论

测试表明，基于FPGA的高斯噪声数字调频算法系统具有运算量小、速度快和可配置的优点，同时还能进行在线升级，达到了预期的效果，具有很好的实用价值。