一类含导数型非线性记忆项的弱耦合半线性*

欧阳柏平

(广州华商学院，广东 广州 511300)

Moore-Gibson-Thompson(MGT)方程因其在实际中的应用[1-2]而得到广泛研究[3-5],本文考虑如下高阶弱耦合半线性 MGT系统柯西问题解的爆破.

(1)

其中，cγi=1/Γ(1-γi),γi∈(0,1),(i=1,2),Γ为第二类欧拉积分;u=u(x,t),v=v(x,t),x∈Rn,t>0;p、q>1;ε>0;βi(i=1,2)>0;(u,ut,utt,v,vt,vtt)(0,x)=ε(u0,u1,u2,v0,v1,v2)(x);需要指出的是，(1)中等式右边含有记忆项的积分表示系统记忆的信息包含着过去的历史信息； 同时(t-s)-γi是衰减的，意味着最近的信息对系统有更大的影响.

(1)中，如果β1=β2,γ1=γ2,p=q，则一定程度上退化为单个的导数型非线性记忆项MGT方程.对于p≠q，此时(1)右端会产生弱耦合现象，由此 (1)已不是单个高阶MGT方程的简单推广. 另一方面，比较相关的弱耦合波动方程研究[6-7]， (1)将出现关于时间t的高阶导数，这将使得无界乘子对其柯西问题解的研究产生很大影响，也导致经典的反射法等技巧无法运用，因为无界乘子的出现使得应用Kato引理进行处理非常困难.本文采用文献[8-10]中提出的高阶双曲方程柯西问题的方法，研究在次临界情况下导数型非线性记忆项对弱耦合MGT系统解的爆破和生命跨度影响.

1 主要结果

首先定义问题(1)的柯西问题能量解.

定义1设(u0,u1,u2,v0,v1,v2)∈(H2(Rn)×H1(Rn)×L2(Rn))×(H2(Rn)×H1(Rn)×L2(Rn)).(u,v)是问题(1)在[0,T)上的能量解，若

且满足

(2)

(3)

应用分部积分对式(2)和(3)进行整理，有

(4)

(5)

由式(4)和(5)可见，当t→T时(u,v)满足问题(1)的能量解的定义.

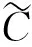
(6)

2 解的生命跨度上界估计

设

(7)

式(4)和(5)中，取φ≡1,φ≡1,{(s,x)∈[0,t]×Rn:|x|≤r+s},可得

(8)

(9)

联立式(7)-(9)，得到

(10)

(11)

式(10)和(11)对t求导，得

(12)

(13)

利用定理1条件和Hölder不等式，有

(14)

(15)

其中c1=c1(n,p),c2=c2(n,p)>0.

联立式(12)-(15)，可推得

(16)

(17)

对式(16)积分，整理得

(18)

由式(17)，同样可得到

(19)

构造U(t)和V(t)的下界序列[11]，设

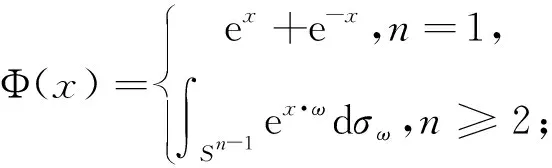
其中Φ(x)为光滑的正函数且ΔΦ(x)=Φ(x);当|x|→∞时,Φ(x)～|x|-(n-1)/2e|x|.

定义函数Ψ=Ψ(t,x)=e-tΦ(x).显然，有-βΨttt+Ψtt-ΔΨ+βΔΨt=0.

引入泛函

(20)

将Ψ应用到式(2)和(3)，应用分部积分和Ψ的性质，可推得

(21)

(22)

其中，

式(21)对t求导，有

(23)

将式(21)和(23)相加，得到

(24)

联立式(20)和(24)，有

(25)

取b1=1/β1，重写式(25)，得到

(26)

G′(t)+(1+b1)G(t)≥b1εI1.

(27)

对式(27)积分，可得

(28)

e2t同乘式(28)两边，积分，整理可得

(29)

其中C1>0.

类似地，由式(20)和(22)，可推出

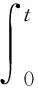
(30)

应用Ψ的渐近性[12]，有

(31)

其中,p′=p/(p-1),p>1;k0>0.

由条件suppv(t,·)⊂Br+t和Hölder不等式，有

(32)

于是，由式(30)和(32)得到

(33)

其中k1=C2pk0-(p-1).

将式(33)代入到式(12)，有

(34)

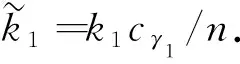
对式(34)求积分，可推出

(35)

同样的处理，有

(36)

构造U(t)和V(t)的迭代序列，令

U(t)≥Dj(r+t)-αj(t-Ljβ1)σj,

(37)

V(t)≥Qj(r+t)-aj(t-Ljβ2)rj；

(38)

其中{Dj}j≥1、{Qj}j≥1、{αj}j≥1、{aj}j≥1、{σj}j≥1和{rj}j≥1均为非负实序列，序列{Lj}j≥1定义为

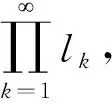
显然，对于j=1，式(35)蕴含式(37)以及式(36)蕴含式(38).设j≥1，式(37)和(38)均成立，以下证明式(37)和(38)对j+1也成立.

联立式(18)和(38)，对于t≥Lj+1max{β1,β2}, 可得

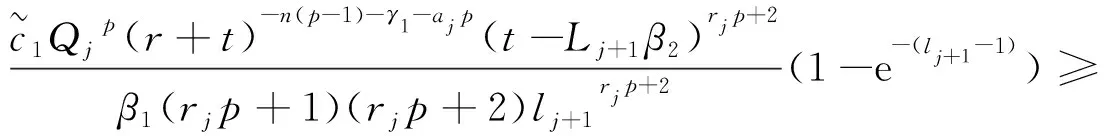
(39)

结合式(19)和(37)，对于t≥Lj+1max{β1,β2}，类似可推得

(40)

取

(41)

(42)

由式(39)-(42)可知，式(37)和(38)对j+1成立.

以下将利用式(41)和(42)对αj,aj,σj,rj进行估计.

当j为奇数时，由递推关系，得到

(43)

aj=n(q-1)+γ2+qαj-1=n(q-1)+γ2+q(n(p-1)+γ1+qaj-2)=…=

(44)

(45)

(46)

j为偶数时，j-1为奇数，此时σj和rj化为

(47)

接下来对Dj和Qj进行估计.利用式(41)和(42)，有

(48)

(49)

由此，进一步可推得

Dj≥K1K2pDj-2pq(pq)-2p(j-1)-2j=M1Dj-2pq(pq)-2p(j-1)-2j,

(50)

Qj≥K2K1qqj-2pq(pq)-2q(j-1)-2j=M2Qj-2pq(pq)-2q(j-1)-2j.

(51)

当j为奇数时，对式(50)和(51)取对数，化简可得

logDj≥logM1+pqlogDj-2-(2p(j-1)+2j)log(pq)≥…≥

(52)

logQj≥logM2+pqlogQj-2-(2q(j-1)+2j)log(pq)≥…≥

(53)

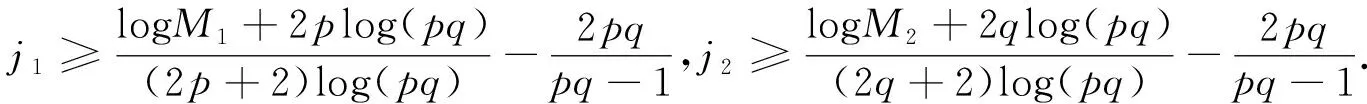
(54)

(55)

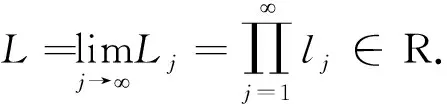
U(t)≥Dj(r+t)-αj(t-Lβ1)σj,

(56)

V(t)≥Qj(r+t)-aj(t-Lβ2)rj；

(57)

其中，j≥max{j1,j2},t≥max{Lβ1,Lβ2}.

令j为奇数，且j≥ max{j1,j2},t≥max{Lβ1,Lβ2}，联立式(43)-(46)以及式(54)-(57)，得到

(58)

(59)

取t≥max{r,2Lβ1,2Lβ2}，由式(58)和(59)可推出

(60)

(61)

式(60)和(61)指数函数中t的指数分别为

(62)

(63)

当式(6)中Θ1(n,p,q,γ1,γ2)>0,Θ2(n,p,q,γ1,γ2)>0时，t的指数为正.

当Θ1(n,p,q,γ1,γ2)>0时，令ε0=ε0(u0,u1,u2,v0,v1,v2,n,p,q,r,β1,β2,γ1,γ2)>0，满足

取j→∞，可得式(61)中U(t)的下界爆破.

同样，当Θ2(n,p,q,γ1,γ2)>0时，对以上ε0,有

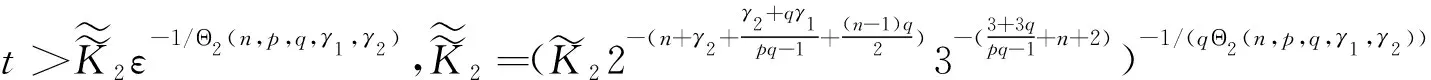
根据上面的讨论可知问题(1)的全局解不存在.另外，可求得(u,v)的生命跨度估计为