离散元法铁粉末压制中粒径分布对力链演化机制的影响1)

张炜 萧伟健 袁传牛 张 宁 刘 焜

* (福建工程学院机械与汽车工程学院,福州 350118)

† (合肥工业大学摩擦学研究所,合肥 230009)

引言

粉末冶金是一种绿色制造技术,广泛应用于机械零件制造等领域,具有节能、节材、高效等特点[1-3].因此,粉末冶金在现代制造业中具有重要地位.而粉末压制工艺作为粉末冶金的重要工序,其可将松散的粉末颗粒制备形成具有一定形状、尺寸以及一定密度和强度的压坯[4-6].在传统粉末压制过程中,主要通过实验获取过程参数,进而分析不同压制参数对压坯成形质量的影响,其往往需要较长的时间周期和较高的成本,而数值模拟方法为粉末压制过程研究提供简便、高效的方式[7-9].

目前对粉末压制成形的数值模拟可从基于宏观尺度的连续介质力学方法[10]和基于微观尺度的离散元法两方面展开.在基于宏观尺度的连续介质力学方法中,粉体被视为各向同性介质,不考虑颗粒之间相互接触的作用力,该方法主要体现于粉体成形有限元模拟中.而由于金属粉末本质为具有离散特征的非连续颗粒物质,颗粒属性如粒径、形状等都对成形后的压坯性能具有明显的影响,因此采用基于微观颗粒的离散元法对金属粉末的压制成形研究将更贴近实际情况.

更为重要的,离散元法(discrete element method,DEM)可对粉末颗粒物质体系中通过常规实验手段无法获取的内部复杂力学结构进行研究,如本研究中重点关注的细观力学结构力链.在颗粒系统中,力通过颗粒间的接触从一个颗粒传递到另一个颗粒,将这一传力特征可视化后得到的链状结构称为力链.力链是贯穿于金属粉末颗粒的一种细观力学尺度承载渠道,对金属粉末压制中传递外部压制力进而促进体系致密化起到至关重要的作用[11].张炜等[12]采用离散元方法对单一粒径分布的金属粉末高速压制过程进行模拟,通过数目、长度、强度、准直系数这四种评估标准对力链特性进行量化研究,但未引入本研究中将探究的颗粒粒径分布影响因素.Meng 等[13]采用离散元方法研究了在压力载荷和剪切速度影响下的平行板颗粒剪切摩擦系统中,单一粒径分布下致密颗粒体系的力链特性,但其力链描述仅基于微观接触力进行.Xu 等[14]采用离散元方法对单一粒径分布的金属粉末单轴压缩过程进行模拟,研究了颗粒的流动状态、力链分布以及主要模型参数对力链的影响,其力链描述同样主要围绕微观接触力进行.综上,粉末压制中力链演化的研究多从微观接触力角度进行描述,未直接实现力链结构的准确提取,同时研究多集中于单种粒径颗粒,对于不同粒径分布粉末压制中的力链行为研究较为有限.

粉末颗粒的直径大小称为粉末粒径,粉末粒径和粒径分布对金属粉末压制成形的压坯致密化程度有着重要的影响,一定程度上决定最终粉末冶金产品零件的性能,因此国内外学者针对金属粉末的粒径分布展开了相关研究.王海陆等[15]通过改变粉末颗粒粒径分布建立仿真模型,分析了不同颗粒粒径下压坯相对密度变化规律与接触力表征的力链分布间的关系,研究发现混合粒径状态下的力链数目远大于单一粒径颗粒情况.闫志巧等[16]对四种不同平均粒径的钛粉进行高速压制成形实验,探究了粉末粒径对压坯密度、最大压制力和脱模力的影响,研究发现在冲击能量较高时,压坯密度取决于粉末粒径,粉末粒径对压坯密度和最大压制力具有相似的影响规律,但对脱模力无明显影响.Skrinjar 等[17]分析了球形粉末的冷压过程,探讨了具有粒径比的粉末对压坯致密化程度的影响,研究发现当粉体小颗粒的比例较高时,粒径比对压坯致密化程度的影响显著.冯威等[18]通过实验研究了粉末粒径与成形压力对无压烧结制备的W-15Cu 复合材料致密度的影响,发现粉末粒径分布越均匀,烧结活性越高,合金性能更加优异,组织结构更加良好,致密度相应提高.孙海霞[19]对三种不同粒径的粉末进行压制烧结,发现在相同温度下,粉末的粒径越小,烧结后压坯致密度越高,表明粒径小的粉末具有较好的烧结活性.上述研究虽然针对不同粒径分布的粉末压制行为进行探究,同时少量研究涉及到力学行为,但针对粒径分布对体系内细观力学结构力链演化机制的影响研究较少,亦未讨论粒径分布对力链演化过程中的力链长度、方向性等量化参数的影响.

综上所述,不同于常见的粉末压制中将粉体视为连续介质的考虑,本研究对微观粉体颗粒进行更为真实的离散元建模分析.同时,目前通过常规实验及理论解析推导等方式难以对粉末颗粒体系中的细观力学结构力链进行直观描述,已有研究中对粉末压制力链结构的准确量化提取存在一定局限性,所采用的力链量化参数亦不充分,且目前研究中虽然部分涉及粉体颗粒粒径分布影响,但针对颗粒粒径分布对粉末压制细观力链的影响讨论较为有限.而本研究中基于离散元理论实现粉末压制行为非连续体建模分析,结合力链提取算法实现力链结构的直观可视化空间分布分析,同时提出通过力链长度、数目、方向性参数对力链行为进行量化描述.此外,进一步讨论了粉体粒径分布与力链行为间的关联机制,建立了颗粒体系结构与力学行为间的联系桥梁,为扩展粉末压制细观力学行为机制提供了理论依据以及为进一步提高金属粉末压坯的致密化程度提供指导.

1 铁粉末压制模拟

1.1 离散元理论

离散元法是由Cundall 等[20]于1979 年提出的一种用于研究非连续颗粒物质结构和运动规律的数值方法,其建立于牛顿第二运动定律基础之上,这与建立在最小势能变分原理基础上的连续介质理论对颗粒物质的描述不同.颗粒物质为液体饱和度小于1,粒径大于1 μm 的离散物质体系[11],颗粒物质体系广泛存在于日常生活中,如自然界中的沙粒,生活中的米粒,而粉末压制中的铁粉亦属于颗粒物质,可基于离散元法的思想对其进行研究.离散元法的核心是运用牛顿第二运动定律[21]对颗粒物质中每个独立颗粒进行运动学分析,因此可得出粉体颗粒力–位移关系式

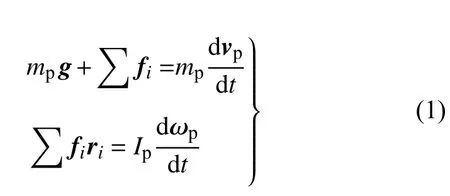
式中,mp为颗粒质量,g为重力加速度,fi为颗粒第i个接触力向量(i=1,2,3,···),vp为颗粒线性运动速度向量,ri为第i个接触力指向颗粒质心的向量,Ip为转动惯量,ωp为颗粒转动角速度向量.

粉末压制过程中,通过离散元法求解的计算流程如图1 所示.

图1 离散元法计算流程图Fig.1 The DEM numerical calculation process

上述离散元法求解过程中,力-位移关系获取的关键为接触力计算.多数学者认为粉末在压制过程中的受力变形过程可分为颗粒位移重排、弹塑性变形及断裂破碎三个阶段[22].由于本文的研究对象铁粉末为非脆性材料,故不考虑断裂破碎阶段,只考虑颗粒位移重排和弹塑性变形阶段.而颗粒位移重排阶段基于牛顿第二运动定律进行,通过相应接触模型体现弹塑性变形阶段.对于粉末颗粒间切向接触力,通过Mindlin-Deresiewicz 接触模型[21]及Coulomb摩擦模型[10]来描述.对于粉末颗粒间法向接触力,在弹性变形阶段,通过Hertz 接触模型[21]来描述,而在塑性变形阶段,通过应力屈服理论[23]来描述粉末塑性变形过程.同时为了更好地模拟粉末压制过程的真实情况,引入局部法向、切向阻尼系数,从而实现运动能量耗散.

在弹性变形阶段,根据Hertz 接触理论,可得到粉末间的法向接触力为

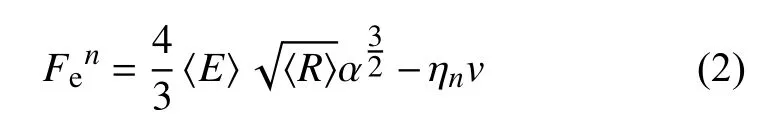
式中,〈E〉 为等效弹性模量,〈R〉 为颗粒间等效接触半径,其中和v2表示相邻两颗粒1 和2 的泊松比,α 为颗粒间重叠量,ηn为法向阻尼系数,v为颗粒间相对速度.

在塑性变形阶段,根据应力屈服理论,颗粒间的法向接触力为

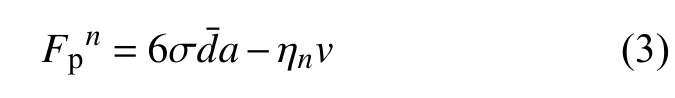
式中,为平均粒径,σ 为屈服应力,其取值由von Mises 屈服准则[23]确定,a为接触半径.

根据Mindlin-Deresiewicz 接触模型及Coulomb摩擦模型,可得到颗粒间切向接触力为

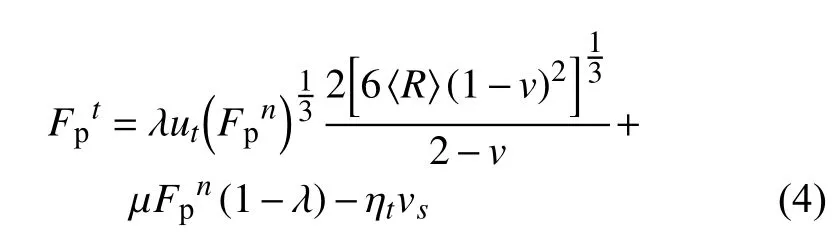
式中,λ 取值与Fpt和Fpn有关,若Fpt＜μFpn,则 λ=1 ;否则 λ=0.ut和vs为颗粒间相对位移和相对滑动速度,ηt为切向阻尼系数,μ 为摩擦因数,〈G〉 为等效剪切模量,其中表示相邻两颗粒1 和2 的剪切模量.

墙体–颗粒间的法向接触刚度、切向接触刚度计算如下

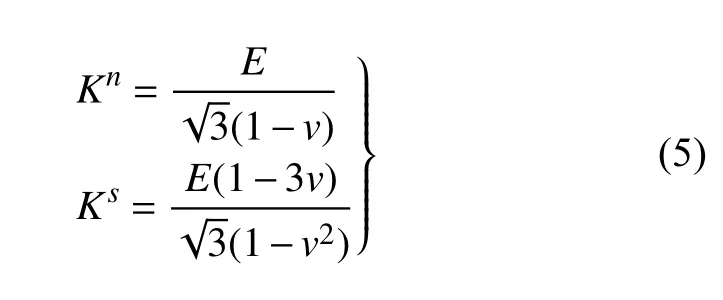
1.2 仿真模型建立

根据上述离散元理论,生成粉末压制模型,如图2所示.

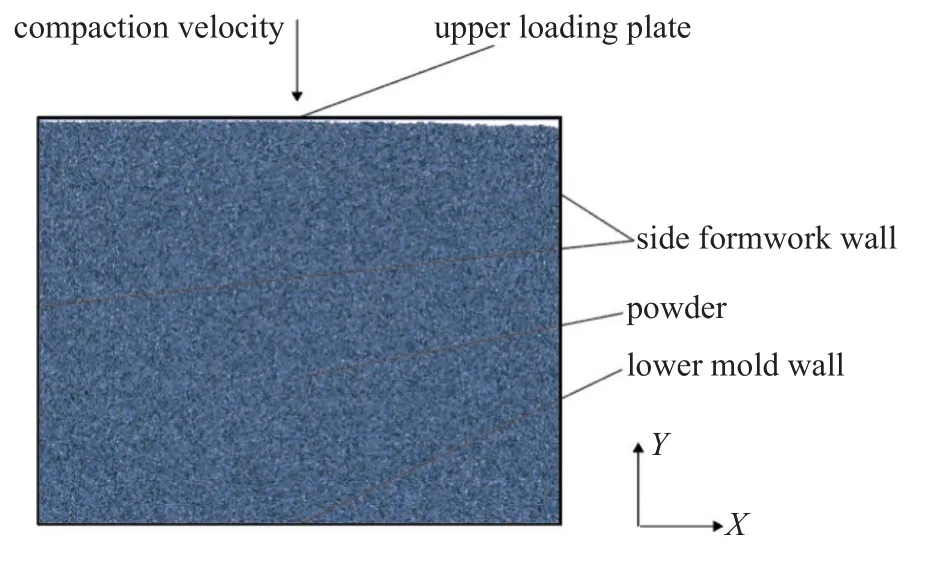
图2 DEM 粉末压制仿真模型Fig.2 DEM simulation model of powder compaction

仿真模型由可做竖直运动的上加载板及两侧和底部固定不动的侧模壁和下模壁构成.模型的宽度为20 mm,高度为14 mm,模型尺寸符合真实粉末压制模具尺寸情况[15].粉末材料参数依据铁粉末颗粒参数选取,铁粉末颗粒物理特征是由颗粒密度 ρ、颗粒间摩擦因数 μp、颗粒泊松比v、颗粒弹性模量E、颗粒剪切模量G、颗粒间法向阻尼系数 ηn和颗粒间切向阻尼系数 ηt这7 个独立的参数来描述的.上加载板、侧模壁和下模壁的物理性质由法向接触刚度Kn、切向接触刚度Ks和颗粒墙体间摩擦因数μpw这3 个独立的参数来描述的,具体的数值如表1 所示[24].模型生成过程如下,首先铁粉末颗粒按照图3所示的粒径分布图[25]通过级配[26]的方式在模壁内随机位置生成,级配方法是通过设定多个颗粒粒径区间从而实现所需颗粒粒径分布的方法.同时为提高计算效率并结合实际情况,本研究将颗粒粒径范围设置为50～180 μm,50～200 μm,50～220 μm以及50～240 μm 四种工况,从而考察不同粒径分布影响.接着通过体积膨胀法(即将颗粒半径先缩小一定比例,随机分布在指定区域,颗粒间无接触和重叠,最后根据孔隙率计算出颗粒所需放大倍数并进行颗粒放大),使得铁粉末体系满足初始体积分数要求(即初始状态时颗粒面积占模型面积的百分比,本模型取值为86%),接着采用重力沉积法使得铁粉末颗粒在重力作用(g=9.8 m/s2,方向沿Y轴负方向)下自然沉积直至体系中各个粉末颗粒的动能接近于零,形成初始粉末堆积.最终生成的模型如图4 所示,不同粒径分布工况下生成颗粒数目分别为36 935,32 900,29 604,26 834,图中左侧色标为生成的颗粒半径参照,从蓝色到红色色标颗粒半径逐渐增大.在进行粉末压制时,保持两侧模壁和下模壁位置固定不动,赋予上加载板恒定压制速度v=5 mm/s,使其沿轴向向下运动(即Y轴负方向)压缩粉体,直至体系体积分数达到94%时终止压制过程.

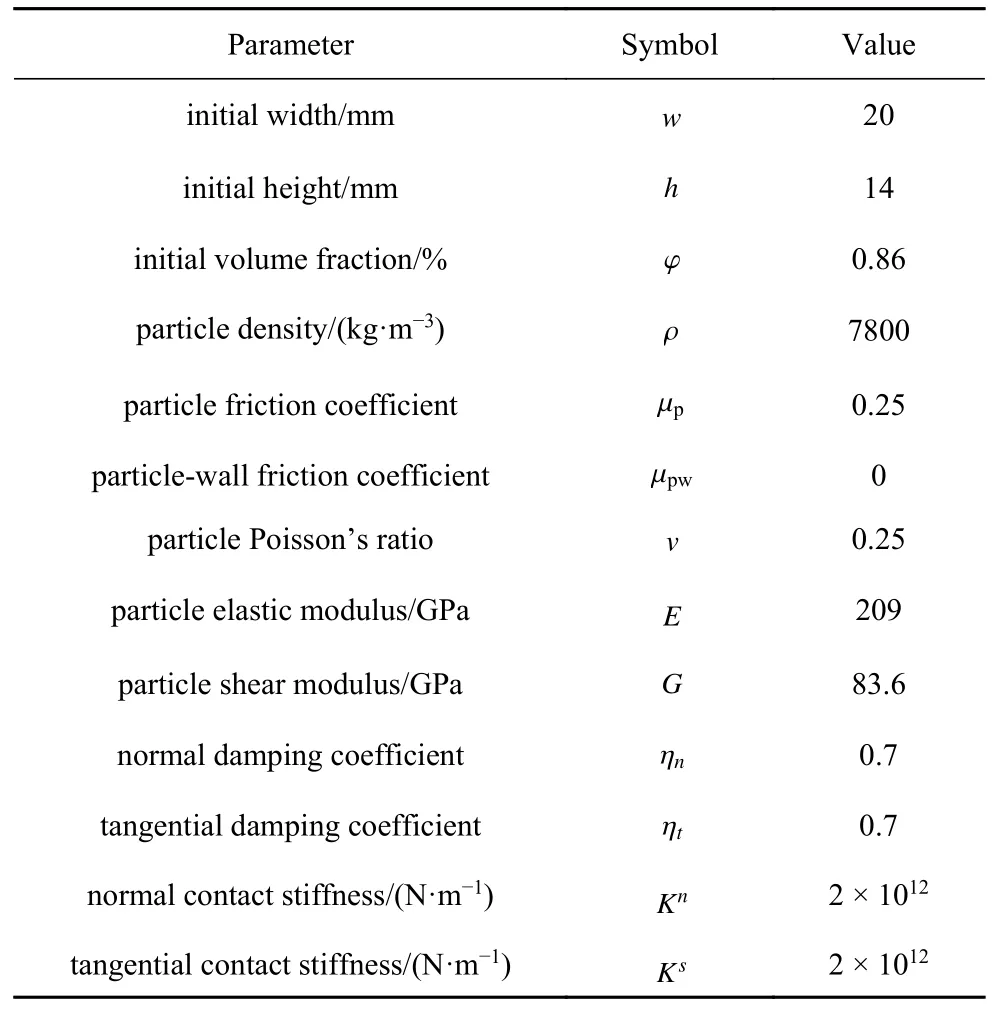
表1 离散元数值模型参数Table 1 Parameters for DEM tests

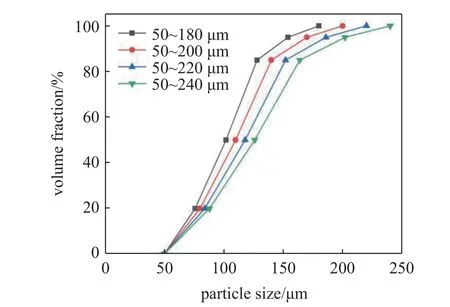
图3 铁粉粒径分布图Fig.3 Iron powder particle size distribution map

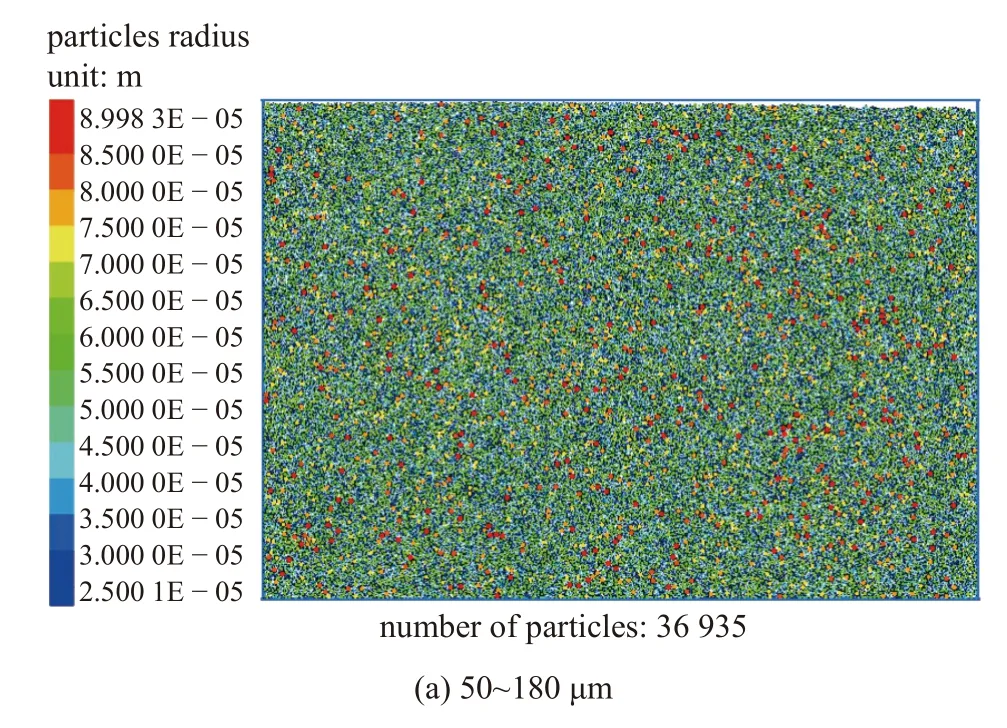
图4 不同粒径分布下模型Fig.4 Model with different particle size distribution

1.3 模型验证

为确保仿真数据的可靠性,需要对模型进行验证.黄培云教授的双对数粉末压制方程可广泛适用于硬质粉末和软质粉末压制,同时该方程适用于等静压制或单轴压制[27].铁粉属于硬质粉末,同时本文研究针对单轴压缩的工况,因此选用黄培云压制方程对模型进行验证.黄培云压制方程如下

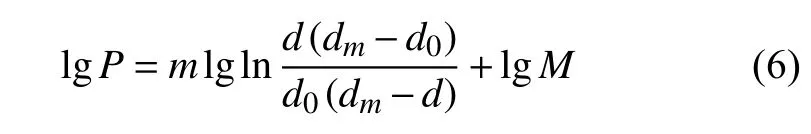
其中,d是粉体密度,通过计算模型的体积分数与金属实际理论密度的乘积得到,dm是金属的理论密度,d0是粉体的初始密度,P是压制压力,通过计算颗粒对上加载板的反作用力得到,M是压制模量,m是硬化指数. lgP是压力参数,是密度参数.

图5 中获取了不同粒径分布的粉体在压制中压力参数 lgP随密度参数的变化规律,由于颗粒在重力作用下沉积,模型上部分出现间隙,导致初始阶段压力参数急剧上升,故不对该部分进行压制方程拟合.粒径为50～180 μm 的模型拟合结果显示相关系数R2=0.988 2 ≈ 1,拟合方程为Y=8.926 79X+4.478 91;粒径为50～200 μm 的粉体拟合结果显示相关系数R2=0.994 1 ≈ 1,拟合方程为Y=8.716 25X+5.148 91;粒径为50～220 μm 的粉体拟合结果显示相关系数R2=0.992 9 ≈ 1,拟合方程为Y=8.655 4X+2.676 09;粒径为50～240 μm 的粉体拟合结果显示相关系数R2=0.991 8 ≈ 1,拟合方程为Y=7.325 79X+3.471 91.各拟合相关系数均接近于1,表明上述不同粒径分布的粉体的模拟结果均与双对数压制方程吻合[27],进而验证了仿真模型的真实性与可靠性.

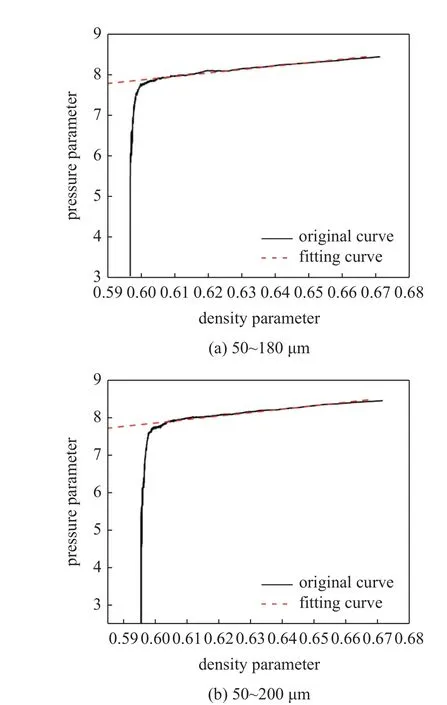
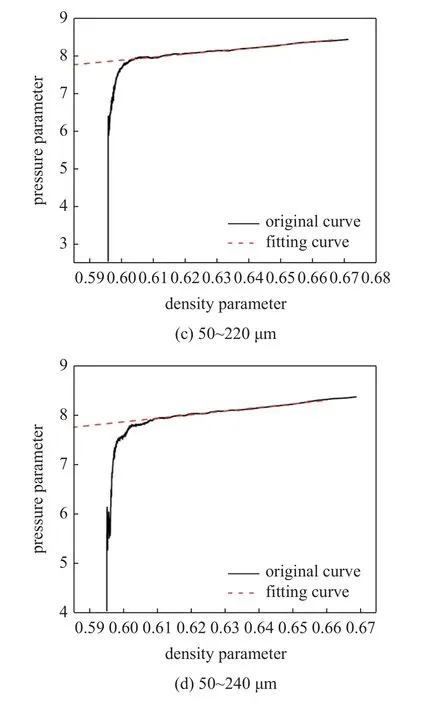
图5 不同粒径粉末压制拟合曲线图Fig.5 Fitting curve of different particle size powder pressing

2 力链的定义及提取方法

在颗粒系统中,将颗粒间的接触力按照成链准则提取得到的链状结构称为力链,力链对金属粉末压制中外部压制力传递起到关键作用.

Peters 等[28]通过主应力法对颗粒进行分析,定义了构成力链所需要的3 个必要条件:

(1)力链由3 个或以上的颗粒组成;

(2)颗粒主应力 σ1大于全部颗粒的平均主应力值,即满足高应力颗粒条件,该条件如式(7)所示

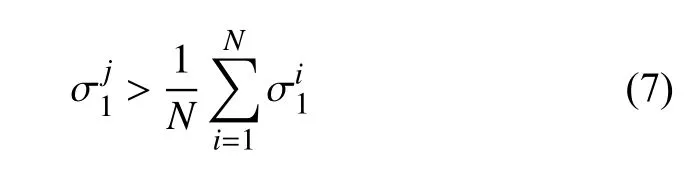
式中,颗粒主应力及其方向的计算如式(8)和式(9)所示

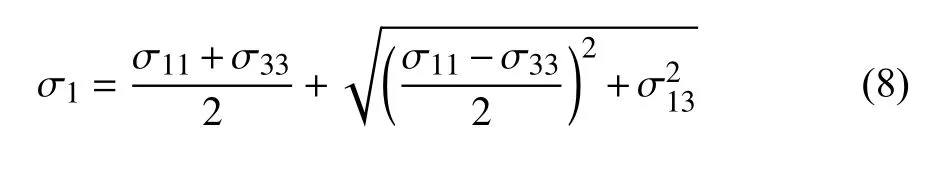
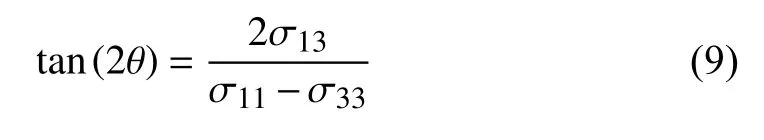
(3)相互接触颗粒的中心连线与主应力方向的夹角小于判别角 α (取45°),如图6 及式(10)所示

式中,σ1i和 σ1j是主应力;N为铁粉末体系的颗粒数;σ11和σ33分别为X方向和Y方向的应力;σ13为X-Y方向的应力; θ 为 σ1的方向; α 是判别角,取45°;l是图6 中连接两颗粒的向量;是相邻颗粒的大主应力向量.

特别地,当两个或两个以上的颗粒在力链搜索时产生分支,应选择角度最小的颗粒.如图6 中P2和P3是与P1相邻的高应力颗粒,由于 β1＞β2,因此选择P3颗粒作为与P1相邻的力链颗粒.

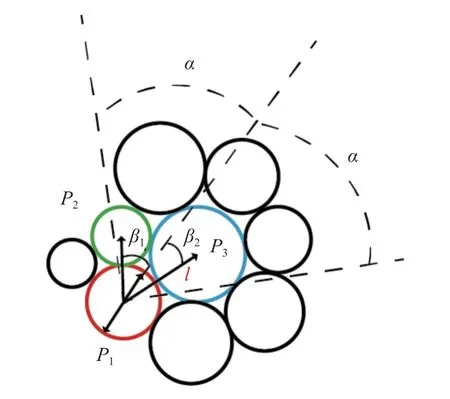
图6 力链分支识别图Fig.6 Force chain branch identification diagram

与接触力判据法[29]相比,主应力法的优势在于每个颗粒往往受多个接触力作用,接触力数目不唯一,而每个颗粒只有一个主应力,能反映颗粒的综合受力状态.因此,本文采用上述主应力法来识别力链,具体识别流程如图7 所示,力链长度L(单位: 颗)表示组成力链的颗粒数.

图7 力链识别流程图Fig.7 Flow chart to identify force chains

3 不同粒径分布铁粉在压制过程中的力链特性分析

3.1 粒径分布对力链分布的影响

结合上述力链结构提取方法,获取四个不同粉末粒径分布模型在粉末压制中力链分布情况,如图8～图11 所示.

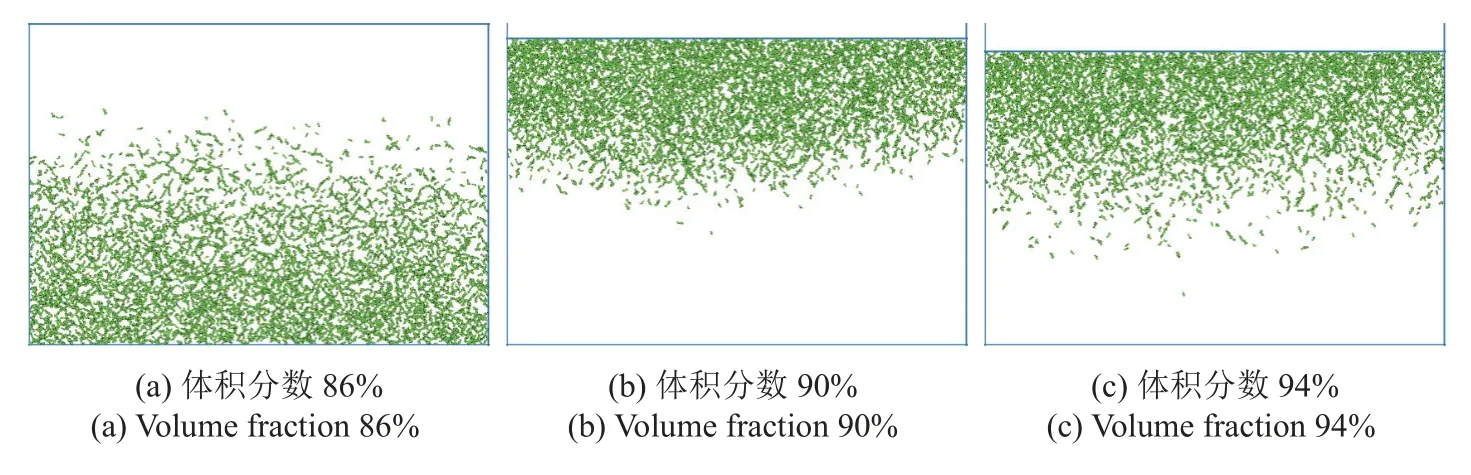
图8 粒径为50～180 μm 模型不同体积分数时的力链分布情况Fig.8 Force chain distribution of 50～180 μm model with different volume fraction

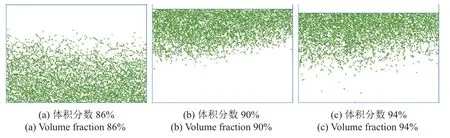
图9 粒径为50～200 μm 模型不同体积分数时的力链分布情况Fig.9 Force chain distribution of 50～200 μm model with different volume fraction

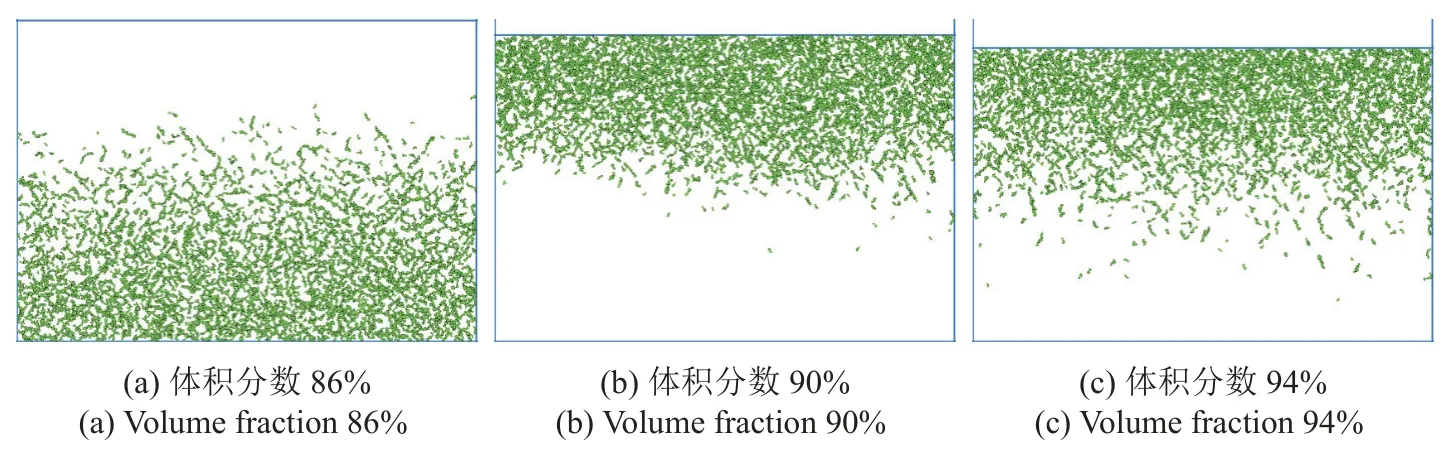
图10 粒径为50～220 μm 模型不同体积分数时的力链分布情况Fig.10 Force chain distribution of 50～220 μm model with different volume fraction

图11 粒径为50～240 μm 模型不同体积分数时的力链分布情况Fig.11 Force chain distribution of 50～240 μm model with different volume fraction

从图8～图11 可以看出,在压制未开始状态,由于重力沉积作用,越接近底部颗粒接触越紧密,力链分布整体集中于体系下部.随着压制的进行,体积分数从86%增加到90%,力链从集中在下部分变成集中在上部分,其主要由于压制过程中的压制力从上加载板施加,导致模型上部分颗粒首先经历力学传递过程造成.当体积分数到达94%时,各个模型中的力链不再变化,且相较于体积分数为90%时的力链状态,体积分数为94%的粉体中力链分布逐渐向底部延伸.由图8～图11 对比可知,当体积分数到达94%时,粒径分布为50～180 μm 的粉体形成的力链分布最集中,且集中于压坯上部分.粒径分布为50～240 μm 的粉体的力链分布最为松散且均匀.在相同初始体积分数下,粒径分布为50～180 μm 的粉体由于级配生成的原因,颗粒粒径相差较小,而粒径分布为50～240 μm 的粉体因其粒径分布更为广泛,颗粒粒径相差较大.在压制时,与颗粒粒径相差较大的粉体相比,颗粒粒径相差较小的粉体其比表面积较大,导致颗粒流动性差,容易发生聚集,从而导致生成的力链分布更为集中.反之,颗粒粒径相差较大的粉体,小颗粒充分填充到大颗粒的间隙,流动性较好,压制力能从大颗粒传递至间隙中的小颗粒,继而形成松散且均匀分布的力链,并促进粉体致密化行为展开.

3.2 粒径分布对力链数目及长度的影响

获取体积分数为94%时不同粒径分布的力链数目及力链长度,如表2 所示.由表2 可知,随粒径分布范围变小,力链总数逐渐增加.其主要原因是粒径分布范围较小时粉体级配生成的颗粒数目最多,颗粒间的相互接触概率较高,颗粒间更易形成紧密接触,在压制力的作用下形成数目更多的力链.

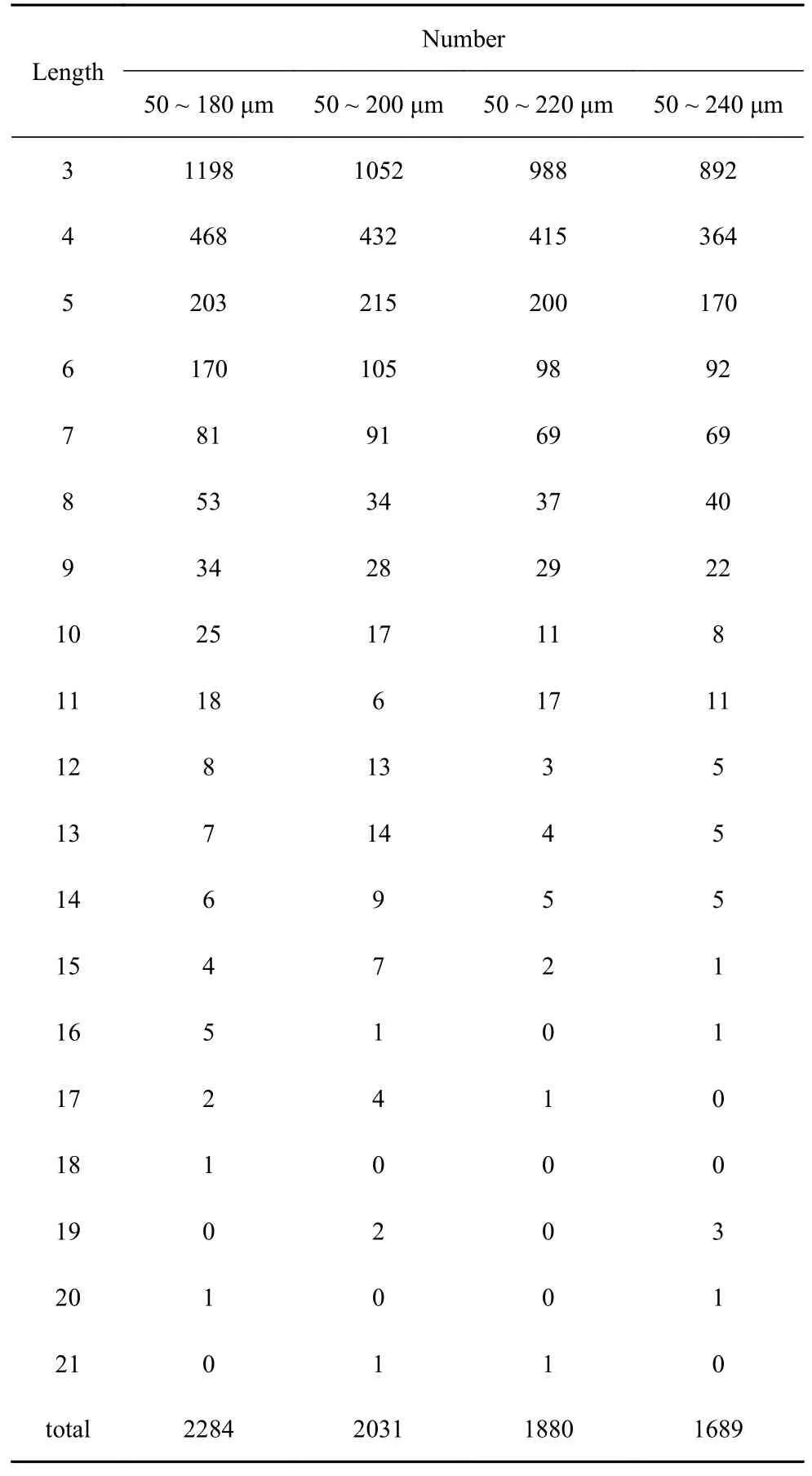
表2 不同粒径分布力链数目及力链长度(φ=94%)Table 2 The number and length of force chains with different particle size distribution (φ=94%)

为了更直观地看出粒径分布对力链长度的影响,将力链按照长度分为三组,分别为力链长度小于6、力链长度为6～13 和力链长度大于13,获取不同粒径分布的力链长度比例如表3 所示.从表3 可以看出,各粒径分布情况下组成短力链的颗粒数即力链长度小于6 的力链数目约占力链总数的84%,同时,力链长度大于13 的长力链数目相对较少,约占1%.不同粒径分布的粉体在压制后的力链数目差异主要集中体现在力链长度小于6 的短力链上,而不同粒径分布对力链长度大于13 的力链无明显影响.该现象主要由于粉末压制中力链经历反复断裂重组过程,长力链容易在外部压力作用下断裂形成较短的力链,短力链所占力链数目比例较高,因此粒径分布影响在短力链上较为集中体现.

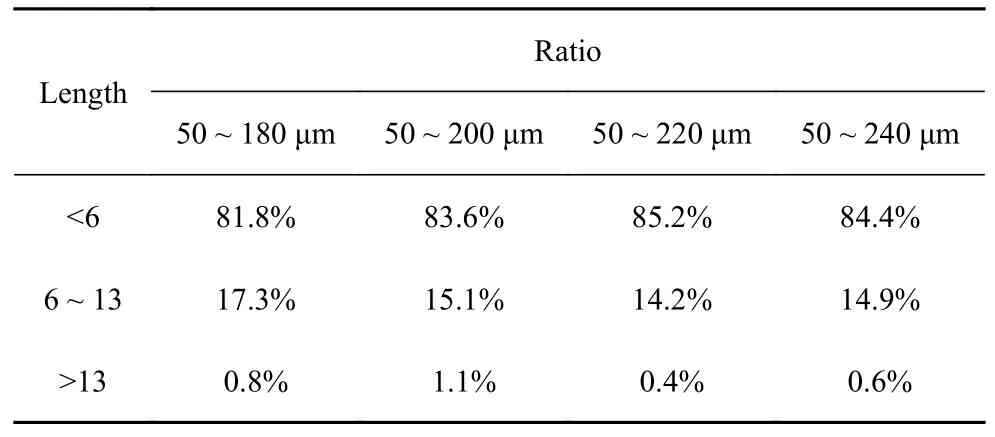
表3 不同粒径分布的力链长度比例(φ=94%)Table 3 Ratio of force chain length with different particle size distribution (φ=94%)

由于力链长度小于6 的力链占据了力链总数的84%,同时相关研究中亦表明短力链对颗粒体系行为影响更为显著[30],进一步分析力链长度小于6的力链更能直观看出不同粒径粉体对力链演化的影响,如图12 所示.由图12 可知,不同粒径分布的粉体在压制过程中力链长度小于6 的短力链数目随着体积分数的增加,均呈现先减少后增加的趋势,其原因是压制开始时颗粒间的接触密度较低,且接触分布较为松散,在外载作用下短力链逐渐重组及拓展生成长力链,因此初始阶段短力链数目逐渐减少,直到压制到体积分数为88%后,体系逐渐变得致密,此时由于压制力的增大,长力链逐渐断裂成短力链的比例逐渐增加,从而造成短力链数目增加.同时研究发现,粉体的粒径分布对颗粒形成力链的数目起着显著影响,表现为粒径分布较大时较短力链数目较少,而当力链数目较少时可对外界载荷起到集中载荷传递作用,外部载荷得以充分传导至体系中各部分,在一定程度上有助于体系形成致密化压坯.

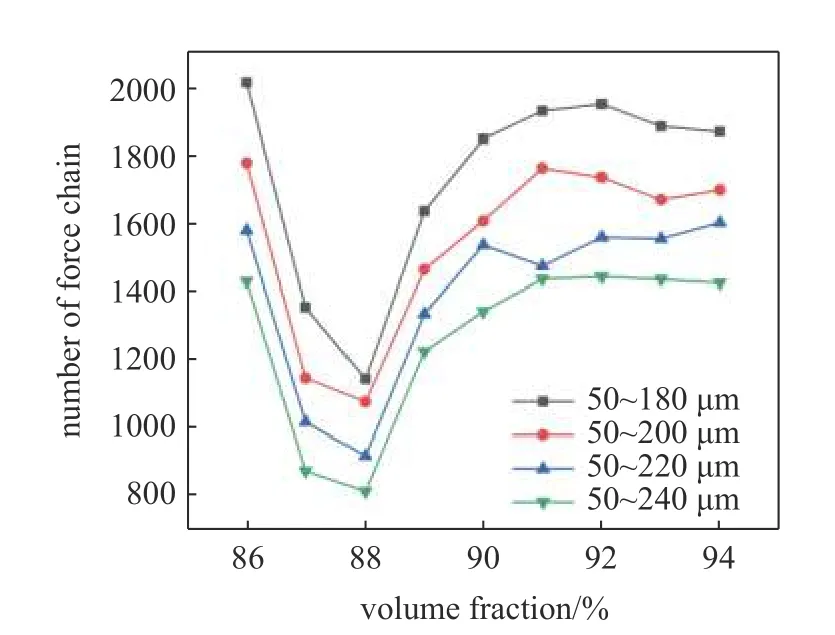
图12 不同粒径分布下力链长度小于6 的短力链数目与体积分数的关系Fig.12 Relationship between the number of short force chains with force chain length less than 6 and volume fraction under different particle size distribution

3.3 粒径分布对力链方向性的影响

为了研究粒径分布对力链方向性的影响,设定力链起始颗粒和结束颗粒形心连线与X轴正方向的夹角 θ 作为力链方向性的参考标准,如图13 所示.由于夹角 θ 在 [0,360] 范围内中心对称,故下文只取[0,180]表示力链方向性的范围,同时以 10°作为区间间隔统计每个区间中力链方向性的分布情况,夹角 θ 越趋于90°,则说明力链方向越倾向于Y轴即垂直方向.

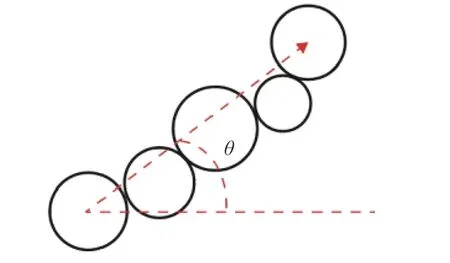
图13 力链方向示意图Fig.13 Schematic diagram of force chain direction

图14 所示为体积分数为94%时不同粒径分布的力链方向分布极坐标图,极坐标轴为力链数目(单位: 条).可知,粒径为50～180 μm 的粉体其力链方向均匀分布在 [50,130] 区间;粒径为50～200 μm 的粉体其力链方向集中于 [60,130] 区间,在 [50,60] 区间最多;粒径为50～220 μm 的粉体其力链方向集中于 [50,80] 和 [110,120] 区间;粒径为50～240 μm 的粉体其力链方向集中于 [50,70] 和 [120,130].随着粒径分布范围的增大,力链的方向由均匀分布转向集中在特定角度范围,同时体现出一定的各向异性.结合前文研究结果,由上述力链方向分布可知粒径分布范围较小时,力链方向分布较均匀,各向异性不显著,而随着粒径分布范围增大,颗粒粒径差异也增大,颗粒流动性增加,在压制力的作用下,力链方向性逐渐将集中于Y轴方向两侧一定偏转角度内,各向异性逐渐加强,即力链方向变为集中在特定角度范围,从而促进体系形成交叉力链网络结构,通过交叉力链网络结构保证外部载荷均分传导,促进粉体致密化行为充分完成.

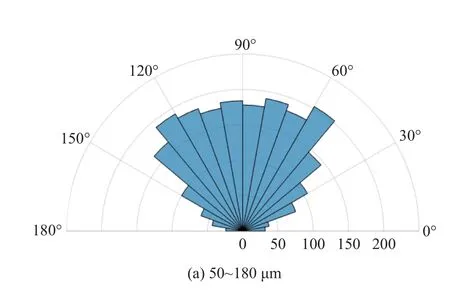
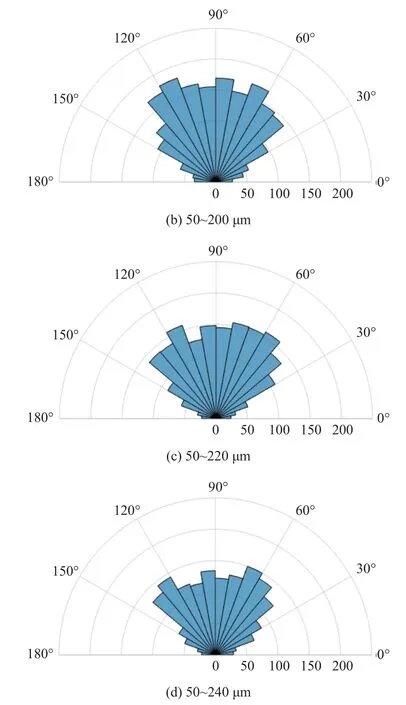
图14 体积分数为94%时不同粒径分布下力链方向性分布情况Fig.14 Directional distribution of force chain under different particle size distribution when the volume fraction is 94%

4 结论

本文基于离散元理论,探究了不同粒径分布铁粉颗粒的压制过程,同时结合力链提取算法获取力链空间分布演化行为,并基于力链长度、数目、方向性量化评估标准,对不同粒径分布下铁粉压制中的力链量化特性进行研究,得到如下结论.

(1)由于不同粒径分布的粉体通过级配生成,颗粒粒径相差不同,导致粉体流动性有差异,颗粒粒径相差较小的粉体其流动性较差,压制时形成的力链空间分布更为集中,而颗粒粒径相差较大的粉体其流动性较好,从而生成的力链空间分布更为松散且均匀,进而有利于粉体致密化进行.

(2)随着粉体的粒径分布范围变大,力链总数逐渐减少.不同粒径分布的粉体在压制过程中力链长度小于6 的短力链数目随着体积分数的增加,均呈现先减少后增加的趋势.同时,粉体的粒径分布对颗粒形成短力链的数目起着显著影响,而对力链长度的影响较为有限,粒径分布较大时较短力链数目较少,可令外界载荷集中传递载荷至体系中各部分,在一定程度上有助于体系形成致密化压坯.

(3)通过对力链方向角度分析发现随着粒径分布范围的增大,颗粒流动性增加,集中于Y轴方向的力链会向两侧屈服,力链的方向由均匀分布转向集中在特定角度,体现出一定的各向异性.同时保证体系形成交叉力链网络结构,并通过交叉力链网络结构实现综合承载,有利于提高粉体致密化程度.