水下发射航行体尾涡不稳定性分析1)

高山 施 瑶, 潘 光 权晓波 鲁杰文

* (西北工业大学航海学院,西安 710072)

† (无人水下运载技术工业和信息化部重点实验室,西安 710072)

** (中国运载火箭技术研究院,北京 100076)

引言

在实际工程中,尾流常常由复杂的三维钝物体产生.即使是一些非常简单的外形,其尾流涡旋结构演变就比圆柱、翼型以及球体等二维物体的尾流结构复杂.在水下垂直发射领域中,常常伴随着复杂的三维湍流流动现象,具有强非线性、高湍流性以及混沌性等典型特征[1].尤其在近尾流湍流区域内,存在着大量尺度不一和强度各异的涡旋结构[2],这些涡旋结构在湍流生成和维持过程中发挥着极其重要作用,同时也是水下连续发射尾流干扰难题的关键影响因素[3].

目前,关于水下发射大多数成果集中在空化水动力与流固耦合特性[4-9].王一伟等[10]在水下发射非定常空化流动方面系统地总结了空化稳定性、溃灭载荷特性以及流动控制等重要物理机制.尤天庆等[11]基于势流理论分析了稳态与非稳态尾空泡流场演变特性,探索了尾空泡瞬态收缩过程对上游航行体物面压力的扰动机理.虽然空化流动现象在水下发射过程显得至关重要,然而由于水下连续发射环境的特殊性,航行体流动干扰可能由其他因素所主导,其中尾流效应是其中最重要的一个影响因素.

长期以来,三维航行体的尾流演变机理都是学者们非常感兴趣的研究课题.因此,学者们为了进一步认识轴对称钝物体的三维尾流涡旋结构,以圆柱、方柱等物体为例开展了大量的研究.李永光等[12]通过实验结果和理论分析相结合方法,首次得出了当有稳定的气液两相涡街发生时,其涡街结构参数与单相流不一致.另外,王智慧等[13]采用PIV 测量手段研究了不同雷诺数下尾迹的速度矢量场和涡量场,发现尾涡的长度、宽度以及脱落频率与雷诺数紧密相关.在此基础上,学者们取得了大量的研究成果[14-18].随着科学技术的发展和研究方法的进步,原本的很多限制逐步被打破,研究对象也从原本的二维结构转向三维结构.高洋洋等[19]研究探索了三维圆柱在不同雷诺数和不同倾斜角度的尾涡流动特性.刘闯等[20]采用大涡模拟方法模拟了高雷诺数下三维圆柱的尾涡结构,发现了高雷诺数下圆柱绕流尾迹变化具有不稳定性.另外,大量研究表明三维圆柱绕流模拟明显比二维更符合实际[21-22].Chen 等[23-24]在三维结构基础之上,研究了湍流动能耗散率和温度耗散率在尾迹中的空间分布,相平均结果表明湍动能耗散率和温度耗散率均集中在卡门涡结构的内部.然而,实际中三维钝物体的尾流常常以大尺度结构存在.Taneda 等[25]提供了油滴在静止水中下落时的尾迹相图,涡环从涡面卷起时立刻失去各自特征,相互生成、相互渗透.Rosenhead 等[26]基于实验结果对此也有相关的解释: 钝物体的尾迹是由一系列不规则的涡环组成,他们的方位是完全随机的,是由涡等脱落位置所确定.夏雪湔等[27]对70°斜切尾钝头旋成体的尾涡结构开展了相关实验研究,发现这类钝物体尾迹中的三维尾涡结构均呈现为多个发卡涡相互连接状态.Shi 等[28-29]也针对水下发射尾流涡结构演变开展了细致的研究,即采用RANS 方法对水下连续发射尾流干扰进行了初步探究,发现尾流中沿轴向间隔排列组成的发卡涡包结构,并对次发航行体的表面压力分布和运动稳定性均有较大的影响.

目前关于尾流涡旋演变机理的相关研究对象主要集中在二维圆柱以及少数的三维钝物体等,然而针对航行体水下发射三维尾流涡旋结构演变机理还处于起步研究阶段.本文的研究工作拟利用改进型延迟分离涡方法对三维航行体水下发射尾流演变过程开展精细化模拟,通过涡识别方法对其尾流区涡旋结构进行识别,研究尾涡结构的演变机理和流场的脉动压力规律,分析不同无量纲横流强度和不同雷诺数下尾涡结构演变差异和脉动压力规律,以期为解决水下连续发射尾流干扰问题提供分析方法和手段.

1 数值方法

1.1 控制方程

水下发射过程涉及水与非凝结气体的混合相流动现象,各相之间存在着强烈的相互作用,导致水下发射过程尾流涡旋结构演变问题具有强烈的非线性和高度的耦合性.本文采用VOF 多相流模型对混合流场进行描述,基本控制方程形式如下

体积分数方程

其中,混合介质密度 ρm=αkρk.

动量方程

其中,μm,λm,F分别表示混合介质动力黏度、混合介质第二黏度以及体力项.

能量方程

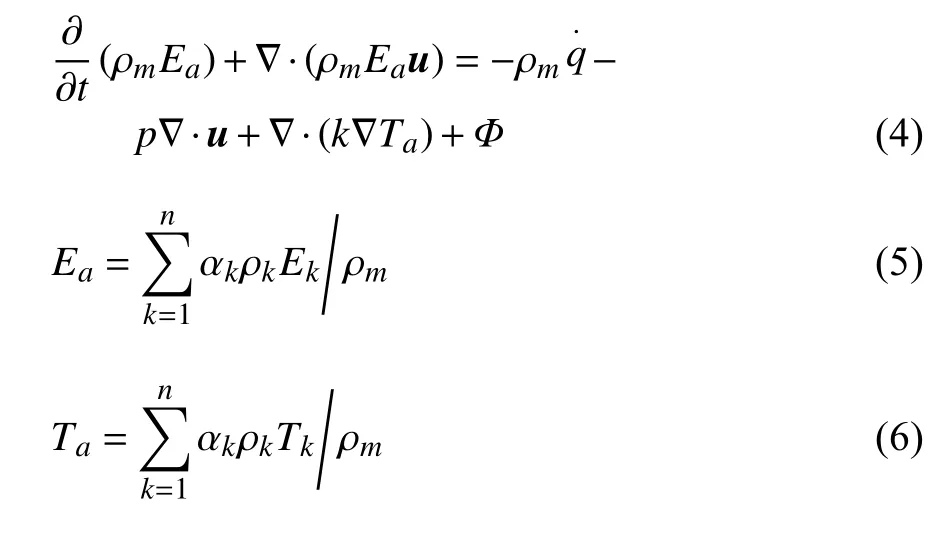
其中,Ea和Ta分别代表混合介质平均能量和平均温度;k和 Φ 分别是热传导率和黏性耗散项.

1.2 湍流模型

本文采用的延迟改进型分离涡IDDES (improved delayed detached eddy simulation)模型基于SSTk-ω模型进行构造,引入湍流长度尺度lIDDES,对模型中湍动能耗散项进行了修正,可以写成

其中,km和 τ 分别是湍流动能和湍流剪切力,Sij是应变率张量,lIDDES的基本形式为

式中,lRANS和lLES分别是RANS 长度尺度和LES 滤波尺度,可表示为

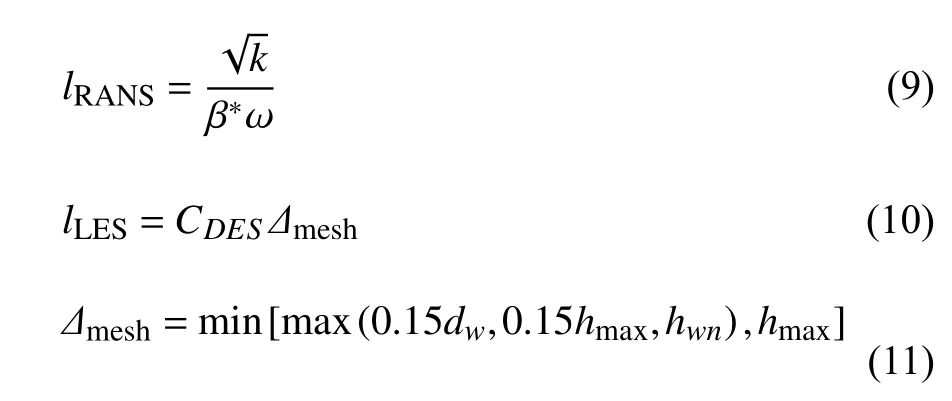
式(10) 中,CDES为模型系数,通常取为0.65;Δmesh为网格尺度;dw为计算点到壁面的距离;hmax为网格最大边长;hwn为垂直壁面方向的网格尺度.另外,本文研究航行体所处的复杂水下环境中最小空化数远远大于半球头型航行体的初始空化数,加之抗空化头型和试验验证.综合分析下,本文未考虑空化影响.

1.3 边界条件与网格细节

如图1 所示,航行体直径为D,长径比L/D=6,其中L是航行体的轴向长度.发射筒轴向长度为 1.2L,直径为D.即发射筒壁面与航行体壁面紧密接触,主要防止筒内高压气体的泄漏.在整个水下发射模拟过程中,采用底部通入高压气体方式将航行体弹射出筒,其中航行体在筒内沿着Z轴正方向加速运动.当航行体尾端离开发射筒口之后,以多自由度方式在水中航行运动,从而完成整个水下发射过程.

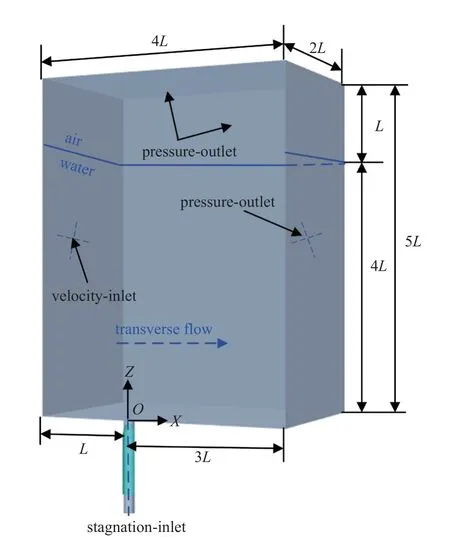
图1 计算域和边界条件示意图Fig.1 Schematic diagram of calculation domain and boundary conditions

本文定义横向来流速度u∞沿着X轴正方向,重力方向沿着Z轴负方向.计算流域长度为 4L,宽度4L,高度 5L.另外,水域高度为 4L,空气域高度为L.计算域左侧为速度入口,底面是壁面,发射筒底端为滞止入口,其余边界条件均为压力出口.滞止入口的压力大小随时间变化,当航行体尾端即将出筒时下降到筒口附近静水压力.为了控制计算量和提高计算效率,沿纵向截取流场计算域,采用二分之一模型开展计算.图2 显示了网格划分细节,背景域和重叠域网格均采用切割体网格,而边界层网格为均匀拉伸的棱柱层网格.为了捕捉尾流区域涡旋结构演化细节,同时与改进型分离涡模型合理匹配,网格细化率取1.3.另外,第一层边界层高度1.5 mm,背景加密域和重叠域网格大小均为0.025D,网格总数是2.8 ×106,并对航行体运动区域和水面附近区域进行网格加密.

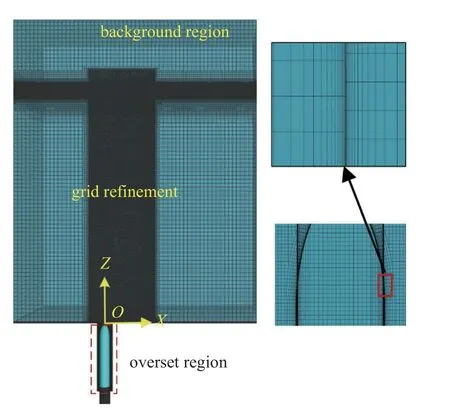
图2 网格划分细节Fig.2 Meshing details

1.4 重叠网格技术

重叠网格方法,又称为嵌套网格技术,其计算原理是: 计算域网格被分割为多块具有重叠或嵌套部分的子网格,其中贴体网格跟随运动体一起运动.数值模拟计算在各个分块子网格上分别进行,而流场信息的传递在重叠边界上通过插值的方式进行,有利于数值计算.因此重叠网格的网格生成难度大大降低,且对模拟多体耦合运动和大转角运动有着很大优势.计算流程如图3 所示.

图3 重叠网格工作流程Fig.3 Workflow of overlapping grids

网格装配主要实现流程为寻点、挖洞和建立插值关系等过程.其中寻点为寻找物理空间点在网格中的相对位置,通过识别包含该空间点的网格单元实现.挖洞则是将背景区域和重叠区域进行耦合,在这个过程中,完全取自重叠区域的网格单元被标记为背景区域中的非活动网格单元,并将非活动网格单元从计算域中删除,从而实现挖洞过程.

1.5 数值计算方法验证

本文设计并搭建了水下发射实验测试装置,并对航行体水下发射过程开展实验与数值计算结果对比与分析.如图4 所示为航行体水下发射试验平台实物图,主要由发射系统、艇速控制系统以及数据采集系统组成.其中,数据采集系统由控制电脑、高速摄像机(Phantom 型)及相应线路等组成.调节白平衡、分辨率(640×1024)、帧率(4000 帧/秒)等参数,以拍到清晰的画面.实验中采用泡沫板来抵消航行体出水惯性载荷的冲击,既保证了实验人员的安全性,同时又防止航行体头型发生撞击而损坏.

图4 实验装置Fig.4 Experimental device

对实验图像的后处理主要是对航行体所处的空间位置的计算和捕捉.根据航行体在整个运动过程中所处于图像中的位置对图像进行区域划分,从而大大减小处理过程中的运算量,同时可以避免其余不必要的背景干扰,提高边缘检测精度和效率.为了获得航行体质心在坐标系下的实际位置,在实验图像中,通过对航行体的标定,可测得图像中每个像素点之间的距离与真实距离的比例关系,通过比例关系可以得到质心以及空泡边缘在坐标系下的实际位置.然而,在实验过程中因为高速摄像机拍摄的实验图像存在有因光线穿过水体和空气间产生的折射误差,需要对提取的边缘散点进行折射校正,校正公式如下

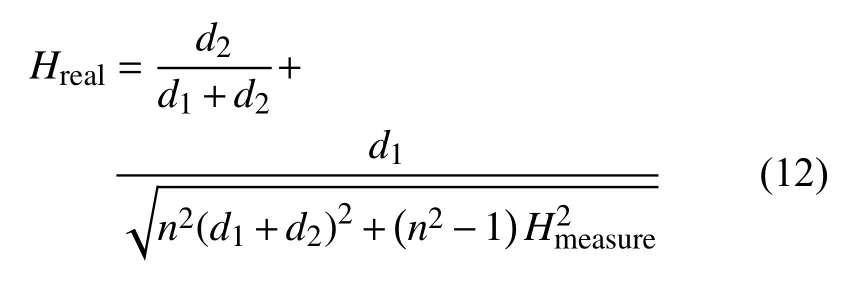
其中,Hmeasure是运动体运动深度的测量值,Hreal是运动体运动深度真实值,d1是运动体距水箱前壁面的距离,d2是高速摄像机镜头距水箱前壁面的距离,n为折射率,如图5 所示.

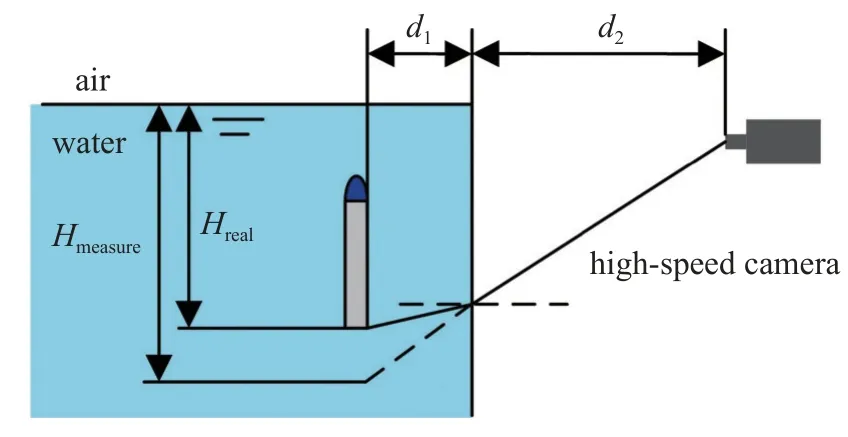
图5 折射校正Fig.5 Refraction correction

基于上述介绍的水下发射实验测试系统和数据处理方法,本文开展了直径20 mm,长度120 mm 的航行体在出筒速度14.3 m/s、平台移动速度0.5 m/s下的实验和数值模拟对比验证工作.图6 和图7 分别给出了数值模拟与实验结果相图对比和运动位移曲线对比.在水下航行阶段,仿真结果和试验吻合度较好.然而,试验中尾空泡由于发射筒口不均匀气团效应导致与模拟结果存在一定的误差.在运动位移方面,数值模拟与实验测试的最大误差为7.52%,验证了本文采用数值模拟方法的合理性.

图6 实验与数值计算相图对比Fig.6 Comparison of phase diagram between experiment and numerical result

图7 实验与模拟计算运动位移对比Fig.7 Comparison of motion displacement between experiment and simulation result

2 结果分析

2.1 瞬态尾流场分析

航行体水下发射过程一般可分为三阶段: 出筒阶段、水中航行阶段以及出水阶段[30].如图8 所示为水下发射过程气液相体积分数演变云图.在横流效应下,航行体带有一定的攻角离开发射筒口时,筒内的高压气体瞬间失去约束,从有界流域向无界流域迅速膨胀.流场中的气团分为三部分: 与管出口相连的气团、附着在航行体尾端的气团(尾空泡),以及在流场内游离的筒口预置气团.由于气团的膨胀、收缩、运动和碰撞等状态变化,将直接对尾流区湍流涡旋流场演变规律具有重要的影响.

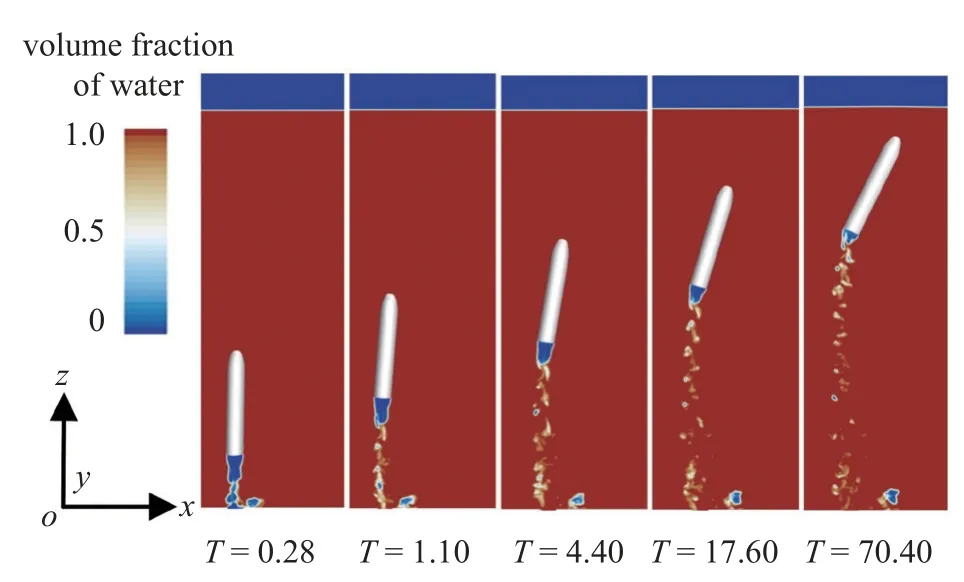
图8 不同时刻下流场气-液相体积分数演化Fig.8 Evolution of gas-liquid volume fraction in flow field at different times

本文涉及的无量纲参数有无量纲时间T、无量纲时间横流强度U以及雷诺数Re,分别定义如下

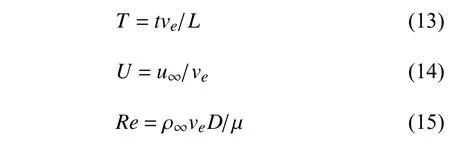
式中,ρ∞和 μ 分别是液态水的密度和黏性系数;u∞和ve分别代表是横流速度和航行体出筒速度;t和μ分别是航行体运动时间和动力黏性系数.

航行体水中航行阶段中,由于尾流高速流体核心区与低速自由流相互作用,呈现出Kelvin-Helmholtz不稳定现象的典型特征,这主要是由于两种速度差混合流中剪切运动所引起的[31-32],如图9 所示.在水中航行阶段,航行体表面附近不断积累涡量.在流动分离作用下,背流侧积累的涡量较多,并在航行体尾端形成脱落涡结构环进入尾流区内.从图10 可知,脱落涡环的核心区交替出现,且沿着X轴正方向运动并发生耗散现象.

图9 不同时刻下流场速度幅值演化Fig.9 Evolution of velocity amplitude in flow field at different times

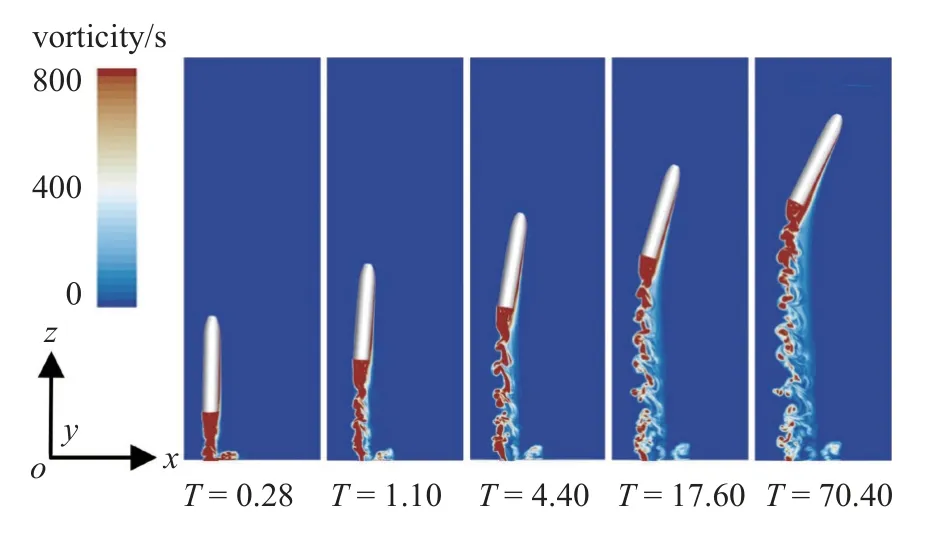
图10 不同时刻下流场涡量幅值演化Fig.10 Evolution of vorticity amplitude in flow field at different times

图11 所示为有无横流条件下航行体头部触及自由液面时刻涡量幅值与等值面尾涡图.由于Q方法难以识别衍生涡以及二次涡,而 λci方法在衍生涡以及二次涡识别过程表现较好[33].因此,本文采用λci准则对尾流区涡旋结构进行了识别.其中,λci准则是在 Δ 准则的基础上进一步发展而来,其数学定义为

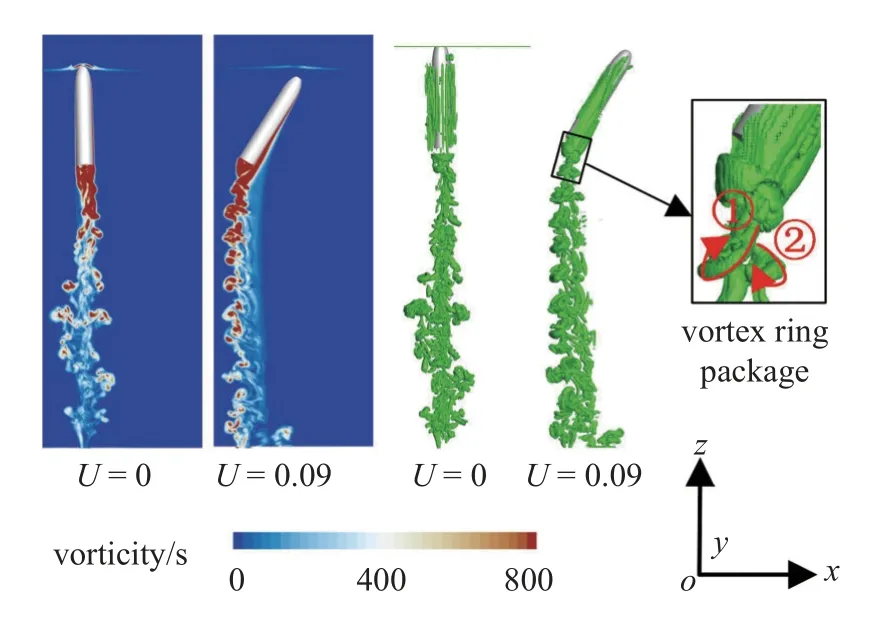
图11 涡量与等值面尾涡演变Fig.11 FIig.11.Evolution of vorticity and isosurface wake vortex

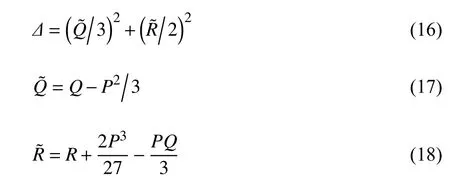
当Δ＞0,其特征值为 λ1=λr,λ2,3=λcr±iλci其中

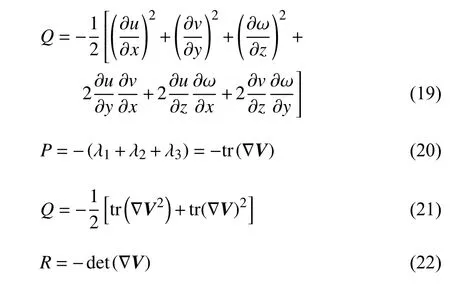
其中,P,Q,R是速度梯度张量 ∇V的三个伽利略不变量. tr 代表矩阵的迹,det 代表矩阵的行列式.

无横流条件下,尾涡结构近似沿着航行体轴线两侧随机分布,而且脱落涡环极易发生破碎,并未形成结构完整的尾涡结构.然而,在横流效应下,当航行体表面附着涡量到达其尾端时,由于其壁面发生旋转,形成低压涡旋,导致流动围绕周围涡核中心,并卷起形成涡环,与横向来流相互作用,发生了准周期性脱落,形成多个涡环,也称为涡环包[29].在此过程中,涡管沿着流向发生拉伸形成涡腿,涡环包与涡腿形成弧状结构发卡涡[34].总体来看,尾涡结构由一系列“发卡涡”相互锁定的“发卡涡包”组成[27],其形态具体表现为不规则状.另外,随着发卡涡包结构的形成,二次涡结构在尾流中也不断衍生并发展.图12显示了不同时刻下等值面尾涡结构演变图.从图中可以发现,单个发卡涡一般不会在航行体尾流区单独存在,而是由多个发卡涡沿轴向间隔排列,组成发卡涡包存在于航行体尾流中.

图12 不同时刻下流场等值面尾涡结构演化Fig.12 Evolution of isosurface wake vortex at different times

为了研究尾流场脉动压力的演变规律,在空间流场内等间距不同位置处设置检测线,如图13 所示,其中压力系数Cp的具体定义为

图13 流场监测线分布Fig.13 Distribution of flow field monitoring lines

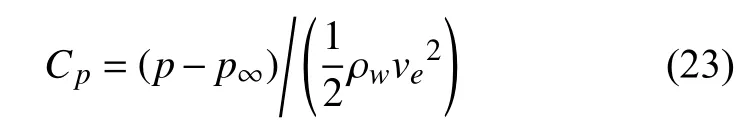
式中,p∞分别是无穷远处当地绝对静压值.

从图14 可以看出,不同监测线出现的第一次峰值时刻均为航行体头部穿过监测位置时刻.然而,进一步分析可以发现,不同监测线的脉动压力曲线均出现了二次峰值,而P4监测线甚至出现了三次峰值,并逐渐减小.在脉动压力的二次峰值出现时刻,此时航行体尾端已离开此位置,因此主要由尾流区涡旋结构演变所主导.

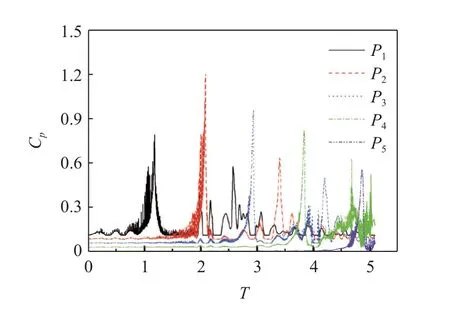
图14 不同监测线脉动压力演变Fig.14 Evolution of fluctuating pressure of different monitoring lines

2.2 不同横流强度下尾流结构演变

为了研究横流强度对尾流场涡旋结构演变机制的影响规律.本文模拟了不同无量纲横流强度U下精细化尾流场演变过程.基于上述无量纲横流强度定义,本文开展了U=0.00,U=0.03,U=0.06,U=0.09 以及U=0.12 下尾流场涡旋结构演变过程研究.如图15 和图16 所示是航行体头部触及自由液面时不同横流强度下尾流场速度与涡量云图.当无量纲横流强度U=0.00 时,即没有横流作用下,尾流高速度核心区与涡核极易发生随机破碎现象,并以较小形态游离在尾流场中,近似沿着航行体轴线两侧分布.随着横流强度的增大,尾流场高速度区破碎现象逐渐减小.当无量纲横流强度U=0.03 时,尾流区速度核心区和涡核虽然结构上发生分离现象,但有紧密靠近趋势.随着横流强度进一步增大,航行体背流侧流动分离强度增加,尾流速度核心区和涡核强度均不断增加,其形态上并未发生明显的分离现象.同时,Kelvin-Helmholtz 不稳定现象的特征愈发明显.另外,当横流强度较小时(U=0.03),涡核近似以小尺度球状形态存在;在横流强度较大时(U=0.12),涡核近似以大尺度片状形态存在于尾流中.

图15 不同横流强度下尾流场速度分布Fig.15 Velocity distribution of wake field under different crossflow intensity

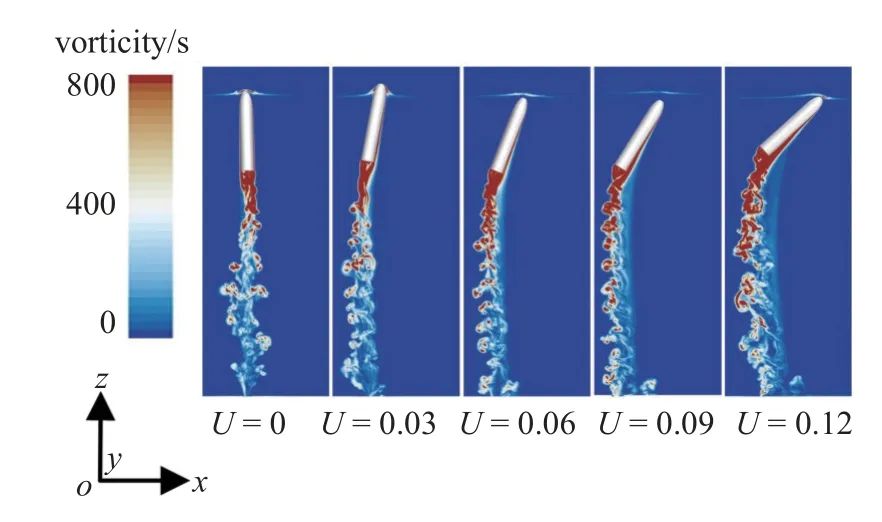
图16 不同横流强度下尾流场涡量分布Fig.16 Vorticity distribution of wake field under different crossflow intensity

图17 给出了不同横流强度下等值面尾涡云图.当无横流强度下,尾涡结构主要以少数脱落涡环以及大量游离的小尺度涡结构组成,并未形成明显的发卡涡结构.当横流强度为U=0.03 时,涡管沿着流向拉伸并向上翘起形成涡腿,并与脱落的涡环形成发卡涡结构.进一步可以发现,此时尾流区主要存在两级涡结构,主涡较为明显的发卡涡包结构,而二级涡结构从尾流中脱落并在流场中形成.在主涡影响下,尾涡结构主要以大尺度不规则涡结构存在于尾流中.随着横流强度不断增大,主涡中发卡涡包尺度不断增强,形成多级准周期的发卡涡结构.当横流强度为U=0.12 时,航行体尾部涡环的脱落频率达到峰值,此时涡管形成涡腿的频率不足以连接已发生脱落涡环的,从而导致发卡涡包形态变得极其不规则.随着横流强度的增加,航行体出筒时刻初始攻角越大,绕流现象愈发明显,导致航行体尾端脱落的涡环频率增加、尺度增大,从而导致尾流中发卡涡包的稳定性减小.

图17 不同横流强度下等值面尾涡分布Fig.17 Wake vortex distribution of isosurface under different crossflow intensity

图18～图20 分别是不同横流强度下P2,P3和P4监测线处脉动压力演变曲线.不同横流强度下,由于尾流引起的脉动压力二次峰值均出现.随着横流强度的增大,P2监测线二次脉动压力峰值先增大后减小,P3监测线二次脉动压力峰值不断增大,而P4监测线出现了三次压力峰值现象,且峰值随着横流强度的增加而增加.因此,可以发现,随着横流强度的增加,尾涡结构演变可近似总结为离散的小尺度涡结构-多级准周期的发卡涡包-大尺度不规则多级涡环碰撞,导致压力出现多次峰值.

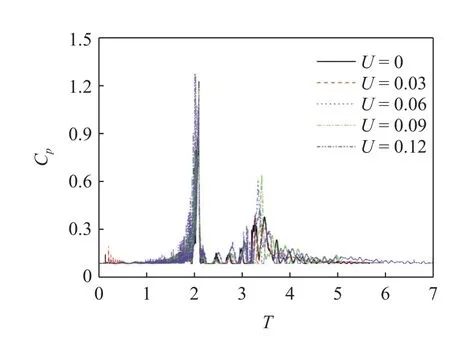
图18 不同横流强度下P2 脉动压力演变Fig.18 Evolution of P2 fluctuating pressure under different crossflow intensities

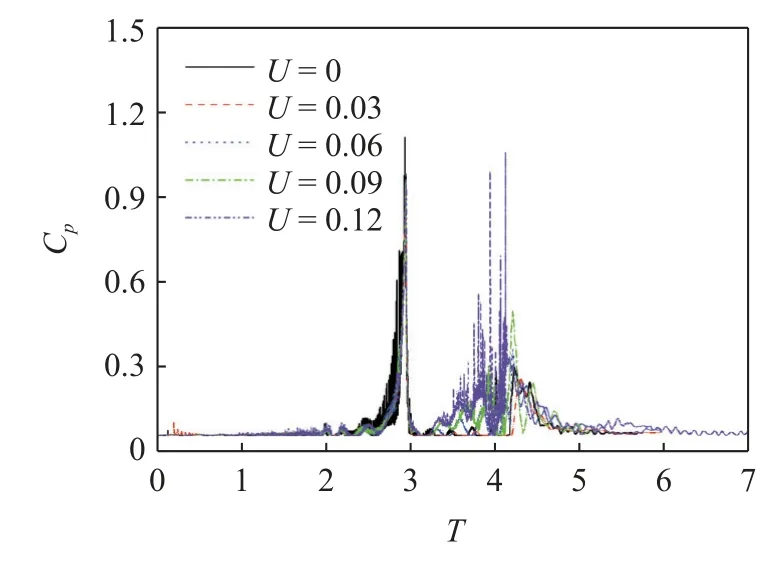
图19 不同横流强度下P3 脉动压力演变Fig.19 Evolution of P3 fluctuating pressure under different crossflow intensities

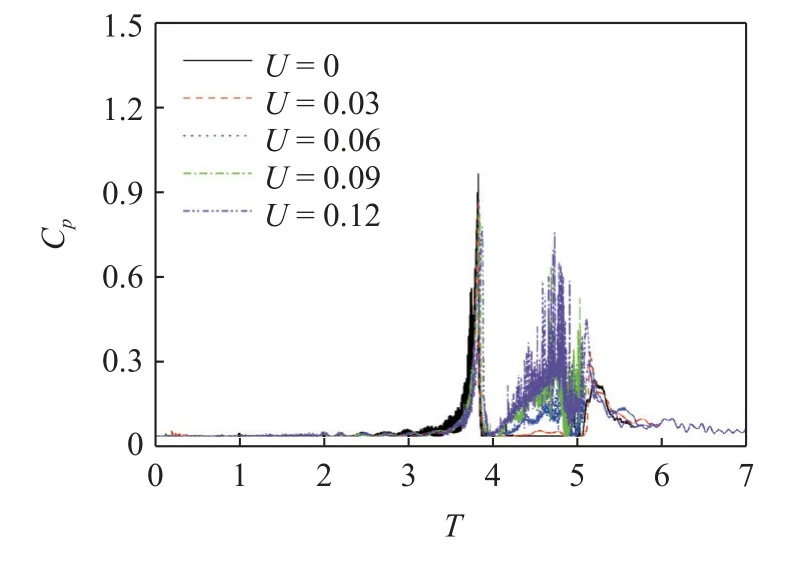
图20 不同横流强度下P4 脉动压力演变Fig.20 Evolution of P4 fluctuating pressure under different crossflow intensities

2.3 不同雷诺数下尾流结构演变

为了研究雷诺数对尾流场涡旋结构演变机制的影响规律,本文模拟了不同雷诺数下精细化尾流场演变过程.基于上述雷诺数定义,本文开展了Re=1.68×105,Re=2.77×105,Re=3.16×105,Re=3.56 ×105下尾流场涡旋结构演变过程研究.

图21 和图22 所示为当航行体头部触及自由液面时不同雷诺数下尾流场速度与涡量云图.随着雷诺数的增大,涡环脱落频率逐渐减小,但尺度逐渐增大.即随着雷诺数的增大,尾涡结构演变可近似总结为: 小尺度-中尺度-大尺度,随机性也不断增强.图23 为不同雷诺数下等值面尾涡云图.另外,随着雷诺数的增大,发卡涡包中涡头的数量明显减小,不规则性增强.值得注意的是: 在高雷诺数下,衍生涡结构逐渐明显,其中衍生涡结构由圆柱形涡和U 型涡组成.当雷诺数较大时(Re=3.56×105),尾流区涡结构演变较为激烈,发卡涡之间相互作用,随机性加强,其基本形态特征消失,逐渐演变为大尺度不规则涡结构.另外,衍生涡结构极为明显,并与主涡结构相互作用,相互影响.图24～图26 分别是不同横流强度下P2,P3和P4监测线处脉动压力演变曲线.可以发现不同监测处脉动压力二次峰值不尽相同,但其涡结构演变对尾流场均产生了一定的扰动现象.

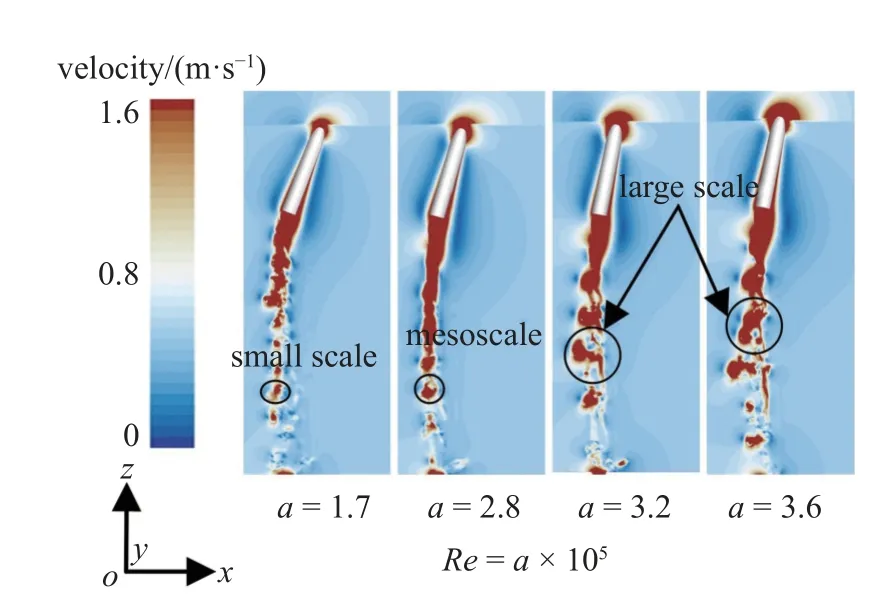
图21 不同雷诺数下尾流场速度分布Fig.21 Velocity distribution of wake field under different Reynolds number

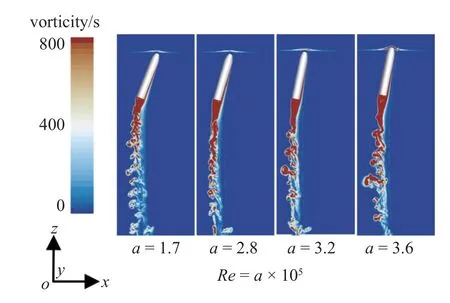
图22 不同雷诺数下尾流场涡量分布Fig.22 Vorticity distribution of wake field under different Reynolds number

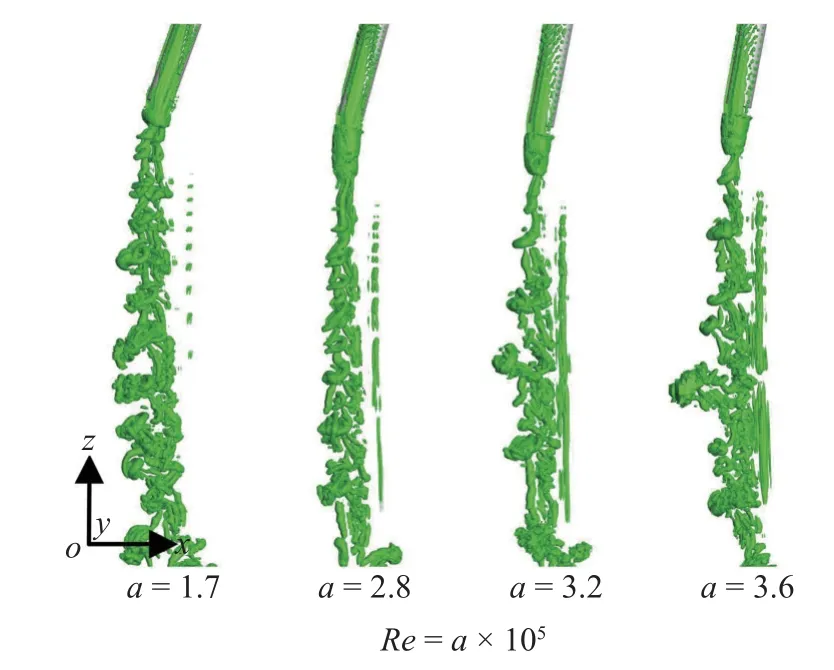
图23 不同雷诺数下等值面尾涡云图Fig.23 Wake vortex distribution of isosurface under different Reynolds number

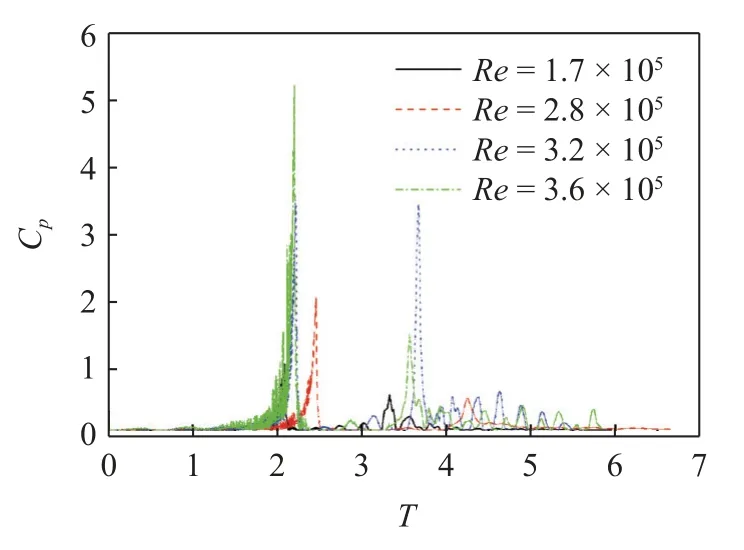
图24 不同雷诺数下P2 脉动压力演变Fig.24 Evolution of P2 fluctuating pressure under different Reynolds number

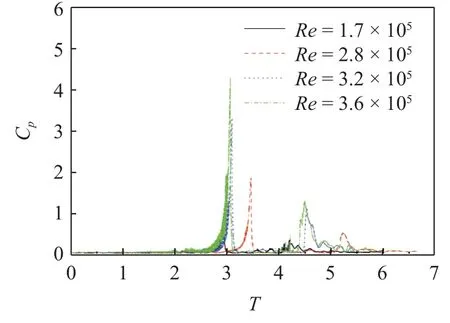
图25 不同雷诺数下P3 脉动压力演变Fig.25 Evolution of P3 fluctuating pressure under different Reynolds number

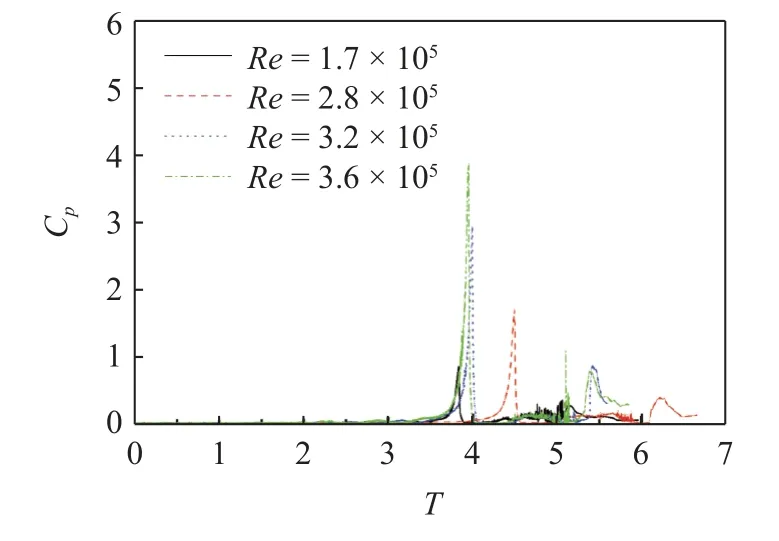
图26 不同雷诺数下P4 脉动压力演变Fig.26 Evolution of P4 fluctuating pressure under different Reynolds number

3 结论

本文基于改进型分离涡模型、VOF 多相流模型以及嵌套网格零间隙技术,建立了横流效应下航行体水下发射数值计算模型,开展了水下发射精细化尾流场数值模拟研究,分析了瞬态尾流场中气液相体积分数、速度、涡量以及涡结构演变,并且进一步讨论了无量纲横流强度(U=0～0.12)和雷诺数(Re=1.68×105～3.56×105)对尾流场中涡旋结构和脉动压力分布特性的影响,具体的结论如下.

(1)水下发射过程尾流区高速流体核心区与低速自由流相互作用,在两种速度差混合流中剪切效应引起尾流区呈现明显的Kelvin-Helmholtz 不稳定现象特征.在横流条件下,涡管沿着流向发生拉伸形成涡腿,脱落的涡环包与涡腿形成发卡形的弧状结构发卡涡.总的来看,发卡涡一般不会单独存在于水下发射尾流中,其结构形态近似呈现由一系列“发卡型”涡相互锁定的不规则的“发卡涡包”.

(2)随着横流强度的增大,尾流速度核心区和涡核强度增加,紧密贴合程度增强.另外,随着横流强度增大,主涡中发卡涡包尺度增强,形成多级准周期的发卡涡包结构.当涡环的脱落频率较大时,涡管形成涡腿不足以连接多个涡环,从而导致发卡涡包形态特征变得不规则,且随机分布性增强.不同横流强度下,导致脉动压力二次峰值均出现的主要原因是尾流涡旋流场演变引起的.

(3)随着雷诺数的增大,衍生涡结构逐渐显现,主要由圆柱形涡和U型涡组成.当雷诺数较大时,发卡涡之间相互作用的强度明显增强,导致其基本形态特征消失,逐渐演变为大尺度不规则涡结构,不稳定性增强.