全方位道集速度建模方法及应用

张丽艳， 李昂， 杨建国， 李士超， 姚玉来， 黄一鸣， 肖飞

中国地质调查局沈阳地质调查中心， 沈阳 110000

0 引言

随着油气勘探开发的精细发展，面对的地质目标越来越复杂，对地震成像的精度要求也越来越高(印兴耀等，2018；常紫娟等，2020)，促使速度建模和偏移方法不断发展.常用的偏移速度建模方法主要包括基于地震波走时速度分析方法、基于波动方程的层析成像方法、基于双程波动方程的非线性波形反演方法、基于波动方程偏移的速度建模方法和全波形反演(FWI)方法.非线性波形反演、波动方程偏移速度建模方法和FWI展示了很好的前景，但是在工业界并未得到广泛的应用，目前工业界使用的主流速度建模方法仍是基于地震波走时层析反演的速度建模方法，如网格层析反演、高斯束层析反演、以及构造和井约束下的层析反演等(张子良等，2020；刘旭明等，2021；郑浩等，2021).在以往窄方位资料处理中，由于受资料限制，在处理中经常忽略各向异性的影响，在速度建模中也并未考虑方位角的信息.伴随着宽方位资料的大量采集，各向异性特征在宽方位数据上表现愈加突出，在处理中也需要考虑速度随方位角的变化，所以，针对宽方位数据的速度建模方法应运而生.Buia等(2011)等提出了分方位处理的思路，将数据按照方位角划分为多个方位，采用分方位处理方式进行层析速度建模，并将方位角信息应用于速度建模中，取得了一定的效果.该技术存在明显的不足是人为干预性强，处理员凭经验将数据体分为多个方位角，并在各个方位角内进行处理，但无论怎样精细划分都存在某些方位角内地震道多，某些方位角内地震道少，最终导致各方位角之间覆盖次数不均衡(Wang et al.，2003；詹仕凡等，2015；李丛等，2022).另外，分方位处理尤其在速度分析和偏移时需要耗费大量的劳动力和处理机时，会严重拉长地震数据处理周期，且多方位层析反演的速度精度不高.伴随着宽方位OVT处理技术的发展，针对宽方位甚至全方位数据的处理流程在业界内得到普遍应用，主要为OVT域道集抽取、OVT域去噪、规则化、偏移以及在偏移后的方位道集上进行方位各向异性处理等，该处理技术流程也是目前宽方位地震处理中广泛采用的流程(陈志刚等，2018；段文胜等，2016；张丽艳等，2021).但是，该处理流程存在两个缺点：第一，OVT域偏移是Kirchhoff叠前时间偏移，速度分析采取的是类似于常规速度分析模式，只是在分析过程中多了一个方位信息的参考，对于构造复杂地区成像精度远远达不到深度偏移成像的精度；第二，在OVT域偏移后的方位道集上进行各向异性分析时容易出现假象，不能确定各向异性的表现特征是由于速度模型精度不够导致的还是地下介质真实的各向异性反映，所以对于各向异性的确定存在多解性.鉴于上述的技术限制，本文提出了基于全方位道集的层析反演速度建模技术，由于OVT域偏移后的全方位道集同时包含方位角和偏移距的信息，所以该技术主要以OVT域偏移后的全方位道集为基础，在全方位道集上拾取剩余时差(包括方位角和偏移距的信息)、进行射线追踪建立方程组，利用层析反演方法统一求解，通过不断迭代最终完成速度建模.反演后的速度能够体现出短波长速度变化，更好地刻画速度变化的细节，有利于提高地质体的成像精度.通过对全方位道集进行层析反演迭代得到最佳的偏移速度，利用此速度进行最终偏移得到的方位道集不存在明显的剩余时差，道集能够得到很好的校平，说明该剩余时差是由于速度模型的精度不高导致的，并不是地下裂缝在方位道集上的真实反映，如果利用上面剩余时差直接进行裂缝预测会产生错误的预测结果.所以，在利用全方位道集进行地下方位各向异性分析或者裂缝预测时，应该在速度模型精度迭代达到极致的条件下进行，这样，各向异性分析才更准确.

1 全方位道集的获得

全方位道集与常规偏移后的CRP道集不同，全方位道集同时包含偏移距和方位角的信息，主要是在OVT处理域实现.OVT概念由Vermeer(1998)提出，后来(Cary，1999；段文胜等，2013)很多学者在方位道集和属性等方面做了深入的研究，形成了针对宽方位数据的OVT域处理理论.OVT域全方位道集的获得主要是在OVT域进行偏移得到，OVT域的形成主要分为三步(Schapper et al.，2009；夏亚良等，2018；康敬程等，2018)：第一，将观测系统中十字交叉排列地震道抽取出来形成十字交叉排列道集.所抽出的十字交叉排列道集按照炮线和检波线等距离划分为若干个小的矩形，每个矩形就是一个OVT片(也称作向量片)，每个OVT片是由相同的炮间距和相同的检波线间距划分而成，具有大致相同的偏移距和方位角(图1a所示)；第二，按照OVT向量片在十字交叉排列中的位置构建坐标系，炮线和检波线的交点为坐标原点，接收线为X轴，炮线为Y轴，向量片中心到坐标原点的距离为偏移距，与坐标原点的连线与纵轴之间的夹角为方位角；第三，按照上述处理方法，对整个工区观测系统抽取若干个十字交叉排列道集，并将具有相同坐标的OVT向量片提取出来，按照相应的Inline号和Crossline号排列起来，形成全区的OVT道集，该OVT道集是单次覆盖数据体(图1b)，类似于常规的一个偏移距数据体，该数据体包含三维空间坐标、偏移距及方位角等信息，为五维数据体.

图1 OVT域实现过程(a) 一个十字交叉排列的OVT向量片； (b) 整个工区的单个OVT体覆盖次数.Fig.1 Procedure of the OVT domain(a) A cross-arranged OVT vector tile； (b) The fold of a single OVT body of the work area.

按照上述过程将宽方位数据转换到OVT域，抽取全区的十字交叉排列，形成全工区的OVT道集.由于每个OVT道集的偏移距和方位角几乎相同，所以OVT道集的能量一致性较好，无论是近偏移距、中偏移距还是远偏移距.图2分别为实际宽方位数据OVT域数据抽取和偏移距域数据抽取后的观测系统，通过对比分析可以看出，理想情况下，一个OVT数据就是对地下一次覆盖的最小数据子集；图2a和图2b分别为共偏移距域和OVT域数据信息对比，可以看出，共偏移距体只包含偏移距的信息，不能体现出方位角的信息，而OVT数据体即包含方位角又包含偏移距的信息，在后续处理中可以充分利用方位角信息进行数据插值、全方位速度建模和裂缝预测等.

图2 偏移距域(a)和OVT域(b)数据对比Fig.2 Comparison of offset domain (a) and OVT domain (b) data

将数据抽取到OVT域后，通过在OVT域进行去噪、插值及偏移等处理，偏移后的道集即为全方位道集，同时包含方位角和偏移距信息.图3a为OVT域处理流程，经过该流程进行处理后得到全方位道集(图3b所示).从全方位道集上可以看出，该道集同时包含炮检距和方位角的信息，图上蓝色曲线代表方位角，方位角方位为从0°～360°呈周期性变化特征，红色曲线代表偏移距信息，偏移距整体趋势是增大的，由于OVT域方位道集具有这个优势，可利用其进行后续的方位各向异性分析和裂缝预测等.

图3 方位道集获得的处理流程及最终的道集(a) OVT域处理； (b) 全方位道集.Fig.3 The sorting process of azimuth gathers and the final gather(a) Processing workflow in OVT domain； (b) Full azimuth gathers.

2 全方位道集网格层析速度建模

常规三维数据速度建模是以Kirchhoff叠前时间偏移得到的共成像点(Common Imagine Point，简称CIG)道集作为输入数据，进行迭代更新得到最终速度(张江杰和张剑锋，2011；张兵和王华忠，2019；吕振宇和魏鹏，2020；徐嘉亮等，2021).由于CIG道集是二维的，只有偏移距(横向)、时间或深度(纵向)，没有方位角信息，所以，这种建模方法适合于常规窄方位地震数据，如图4所示的建模流程.该流程中速度建模的输入道集是常规深度偏移形成的CIG道集，道集为二维的，不存在分方位的情况.在CIG道集上拾取剩余时差、进行射线追踪建立反演方程组，整个建模过程中不体现方位角的信息(张建明等，2021).随着宽方位地震采集的发展，针对宽方位数据的速度建模技术也逐步得到发展，为了充分利用方位角信息，发挥宽方位的优势，速度建模逐渐发展为分方位建模的方法，将宽方位数据人为划分几个扇区，在每个扇区内利用同一速度进行深度偏移，得到不同方位扇区的CIG道集，在CIG道集上分别拾取剩余时差并进行射线追踪，然后统一建立方程组并求解，得到速度模型，通过对上述过程不断迭代、更新得到最佳的速度模型(图4b所示).这种分方位层析反演速度建模的方法在一定程度上体现了宽方位数据处理的优势，间接的反映了方位角的信息，但是存在的弊端是人为干预性太强，人为划分方位角扇区会导致不同扇区间的覆盖次数不均匀，另外，工作量会大大的增加，划分几个扇区就需要进行几次的深度偏移，而且在每个扇区内分别拾取剩余时差也会带来巨大的工作量，求解的精度不高，很难精细刻画速度变化的细节.

随着OVT域处理技术的发展，OVT域层析反演速度建模技术逐渐成为OVT域处理中一个重要环节.虽然OVT域速度建模不存在类似前面人为划分方位的情况，但是目前OVT域建模所采用的道集仍沿用于以往的常规共偏移距道集(图4c所示).首先对宽方位数据进行OVT域转换，在OVT域进行去噪、规则化等处理，然后利用常规成像方法进行偏移成像，得到CIG道集，但此时的道集同样不包含方位角的信息，利用CIG道集进行速度建模，再利用得到的速度模型进行OVT域偏移，得到偏移后的全方位道集，再对全方位道集进行方位各向异性处理.这种方法的缺点是偏移后得到的方位道集上存在的剩余时差不一定是地下裂缝的真实反映，可能是速度模型精度不够导致的，所以，利用此方位道集进行裂缝预测等分析时可能存在不确定性.基于上述技术弊端，本文提出了真正的宽方位OVT域层析反演速度建模方法，对OVT域偏移后的全方位道集统一拾取剩余时差，统一建立方程组，统一层析反演，进行迭代求解出最佳速度，速度建模流程如图4d所示.拾取的剩余时差是采用全三维的Poisson方程算法求解，该算法是在角度域实现的.这样既可保留方位的信息，同时又减少了人为分方位的干预因素，能够更好地刻画速度模型变化的细节，提高地质体的成像精度.

综上所述，现有的宽方位数据建模方法与本文提出的OVT域建模方法存在一定的区别，主要体现在以下几方面：

(1)速度建模的输入道集不一样.常规速度建模和分方位速度建模输入的道集是CIG道集，道集为二维的，不含方位角的信息；OVT域速度建模输入的道集是OVT域偏移后的方位道集，道集中直接包含方位角和偏移距的信息.

(2)用于构建拾取剩余时差的方程不一样.常规速度建模剩余时差拾取是在CIG道集上直接拾取，进行射线追踪建立反演方程组，整个建模过程中不体现方位角的信息；分方位速度建模是偏移后的道集上拾取剩余时差，分别进行射线追踪，建立N个方位的反演方程组，最终进行迭代求解；OVT域速度建模是在OVT域全方位道集上拾取剩余时差，统一进行射线追踪，统一建立反演方程组迭代求解.

(3)建模的工作量和最终得到的速度精度不同.常规速度建模方法的工作量最小，但是最终得到的速度模型精度最低，分方位建模方法的工作量最大，速度模型精度次之，OVT域建模方法工作量介于二者之间，但是得到的速度精度最高.

OVT域层析反演是在OVT域偏移后的全方位各向异性道集上进行剩余时差拾取，并采用Poisson方程算法进行求解.由于Poisson方程是通过笛卡尔坐标系表示的，而OVT域方位各向异性道集剩余时差需要考虑方位角的信息，因此需要将方位各向异性道集炮检距转换成反射角，再将反射角分别分解为沿Inline方向和Crossline方向的分量，并采用笛卡尔坐标系表示.反射角和方位角与x、y的关系可表示为：

x=γ1cosγ2，

(1)

y=γ1sinγ2，

(2)

式中γ1为反射角，γ2为方位角.

在笛卡尔坐标系中，深度剩余时差τ(x,y)可表示为三维数据体上的一个曲面.τ(x,y)是Poisson方程的解：

(3)

(4)

利用上述Poisson算法对OVT域偏移后的方位道集拾取剩余时差，然后根据剩余时差进行射线追踪、建立反演方程进行层析反演迭代得到速度更新量.

根据拾取的剩余时差，进行网格层析反演，将地下划分为n个包含速度信息的立方体网格，与速度之间的关系可用矩阵表示：

(5)

其中，δti表示在方位道集上第i道的走时误差，Dij表示道集中第i道在第j个网格中的射线路径长度；δsi表示第j个网格中的慢度误差.反演后得到不同方位的速度，利用速度参数进行椭圆拟合求取.通过之前求取的不同方位的群速度v和对应的方位角α求解公式(6)，可获得快速度vfast和慢速度vslow以及方位角φ.式(6)为：

(6)

3 应用实例

将上述层析反演速度建模原理应用于某工区宽方位地震数据的速度建模中，该工区宽方位资料采集为正交观测系统，横纵比为0.9，面元5 m×5 m，覆盖次数为256次，属于小面元、高覆盖采集.将预处理后的CMP道集抽取到OVT域，得到OVT道集，OVT道集的个数与全区的覆盖次数基本相同，为256个OVT道集.每个OVT道集是一个单次覆盖数据体，具有统一的炮检距和方位角.该宽方位数据建模之前需要进行预处理，主要包括：OVT域去噪、抽取OVT方位道集、针对OVT道集进行叠前规则化、偏移处理，这样得到偏移后的方位各向异性道集保留有偏移距和方位角的信息，此时的方位道集不需要做各向异性处理，用于后续建模中剩余时差的拾取，偏移速度可作为速度建模的初始速度模型.图5是常规深度偏移得到的CIG道集和OVT域深度偏移得到的方位各向异性道集，二者所用的速度模型是相同的，图中绿色曲线是偏移距的变化，紫色曲线是方位角的变化，图5a中CIG道集没有体现方位的变化，所以紫色曲线是一条水平直线，而图5b中方位各向异性道集的方位角是周期变化的.通过二者对比可以看出，常规深度偏移的CIG道集看似完全校平了，速度比较准确，但是在图5b方位各向异性道集上存在明显的随方位起伏变化的时差现象，这个时差随方位角有规律的变化，尤其是图中2500～3000 m深处(红色方框标注处)，由此可说明现有的速度是不能将方位道集校平的.那么方位道集的时差究竟是速度模型精度不够导致的还是地下方位各向异性特征的真实反映呢？通过研究认为，该地区偏移后的方位各向异性道集上产生的剩余时差是由于偏移速度模型的精度不够导致的.由于常规偏移距域速度建模方法没有考虑方位信息，速度反演和平滑是采用的大尺度速度参数，不能体现小尺度的速度扰动.按照原来的深度偏移和速度更新方法，即使速度平滑的尺度变小，也不能达到所需的精度.如果在OVT域宽方位数据层析反演速度建模中将方位角信息加入到速度反演迭代中，且此过程中将平滑参数从相对大尺度逐步迭代为小尺度，解决速度细节问题，才能真正消除剩余时差的影响，因为速度变化的细节是解决剩余时差的关键因素.针对上述分析，在OVT域进行层析反演速度建模，采用Poisson算法在方位各向异性道集上进行剩余时差拾取，逐步迭代，速度网格参数逐步缩小，横向和纵向平滑参数逐步缩小，横向平滑参数由2800 m减小到1800 m到最终800 m，纵向平滑参数从600 m减小到400 m再到200 m，逐步提高地质体成像精度.

图5 CIG道集和方位各向异性道集的对比(a) 常规偏移的CIG道集； (b) OVT域偏移的方位各向异性道集.Fig.5 Comparison of the CIG gathers and the azimuth anisotropic gathers in OVT domain(a) CIG gathers of conventional migration； (b) Azimuth gathers anisotropic migration in OVT domain.

图6a和图6b分别为初始速度模型和OVT域层析速度反演迭代后得到的速度模型，可以看，通过OVT域层析反演迭代后得到的最终速度更能够很好的刻画速度变化的细节(图中2000 m以下).图7为初始偏移的方位各向异性道集和迭代后最终偏移的方位各向异性道集，通过二者对比可以看出，初始偏移的道集上存在着很强的随方位变化的剩余时差，通过迭代后，速度精度得到提高，方位各向异性道集得到了很好的校平，剩余时差得到了较好的消除(图中红色方框标注处).由此可以看出，该地区方位道集上的剩余时差并不是地下方位各向异性特征的真实反映，而是由于速度模型的精度低导致的.虽然前期的处理中经过多次的迭代不断的提高速度精度，但是传统的深度偏移速度建模中缺少方位信息，射线追踪时也没有考虑不同方位的变化，所以不能很好的刻画速度变化的细节，因此只能反映大尺度的信息，而OVT域偏移能有效地保存方位信息，通过多次反演迭代，最终得到的速度模型能够反演出小尺度的速度变化细节.

图6 OVT域初始速度模型(a)和最终迭代速度模型(b)的对比Fig.6 Comparison of the initial velocity model (a) and the final iterative velocity model (b) in OVT domain

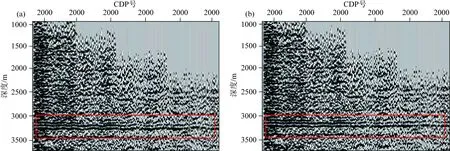
图7 OVT域初始偏移方位各向异性道集(a)和最终迭代偏移的方位各向异性道集(b)对比Fig.7 Comparison of the azimuth anisotropic gather of the initial migration (a) and the final iterative migration (b) in OVT domain

图8为OVT域初始偏移和最终偏移剖面的对比，可以看出由于速度模型的不断更新迭代能够得到更精确的速度，使得最终偏移成像的精度大幅度提高，尤其是整个基底的轮廓非常清晰，很好的刻画了整个构造的细节变化，基底以下内幕成像及陡倾角地层成像得到改进，地层接触关系更清楚(图中绿色椭圆标注部分)，为后续的解释、储层预测提供了可靠的数据保障.

图8 OVT域初始偏移剖面(a)和最终迭代偏移剖面(b)对比Fig.8 Comparison of the initial migration section (a) and the final iterative migration section (b) in OVT domain

4 结论

(1)当地下介质为方位各向异性介质时，方位各向异性会导致剩余时差随方位的变化，影响成像精度，地震成像处理过程中，消除方位各向异性可以减小剩余时差随方位的变化，有利于进行同相叠加，提高成像精度.但是，在实际地震资料裂缝检测中，需要利用方位道集的剩余时差进行各向异性分析，方位道集的剩余时差可能是由速度精度不高导致也可能是地下介质真实的各向异性反映.

(2)常规层析反演速度建模方法没有利用方位角的信息，OVT域全方位道集层析反演速度建模方法充分利用方位角信息的同时又能够减少分方位的速度剩余时差拾取的工作量，更灵活有效，能够很好地刻画速度变化的细节.

(3)实际资料应用研究表明，OVT域全方位道集层析反演速度建模方法能够很好地解决该区的剩余时差问题，将方位各向异性道集校平，由此可知，方位道集的剩余时差并非是该地区地下介质方位各向异性的真实反映，而是由于速度精度不够导致的.因此利用OVT域方位道集进行裂缝预测时，应该消除由于速度精度不高带来的误差，这样，在此基础上进行各向异性分析和裂缝预测的结果才更可靠.

致谢感谢CGG地球物理公司及大庆油田勘探开发研究院提供技术支持.