利用GNSS垂直位移研究长江流域陆地水储量变化的时空分布特征
汤苗, 钟萍*, 姜中山, 刘晚纯, 成帅, 杨兴海
1 西南交通大学地球科学与环境工程学院, 成都 611756 2 湖南省交通规划勘察设计院有限公司, 长沙 410219
0 引言
陆地水储量(Terrestrial Water Storage, TWS)通常定义为存储在地表、土壤、地下、冰雪、树冠以及生物当中水分的总和(Famiglietti, 2004; Wahr et al., 2004).与大气、海洋负荷不同,陆地水储量往往因缺少可靠的观测数据而难以量化(Dai and Trenberth, 2002).因此,传统的陆地水储量研究一般通过气象数据结合地表模型建立的水文模型进行,但这些数学模型未对所有水成分完整建模,并且低估了人为影响以及气候变迁导致的陆地水异常情况(Scanlon et al., 2018).现代卫星大地测量技术的发展为陆地水储量变化研究提供了革命性的工具,例如卫星重力观测技术、全球卫星定位系统等长达数十年的连续观测为水储量变化研究提供了宝贵的基础数据(重力场、地表变形数据)(Tapley et al., 2004; Argus et al., 2014),这些数据能够反映所有水成分的总体变化情况,弥补了水文学研究中地表及地下水实测值不足的缺陷.
重力恢复与气候试验GRACE (Gravity Recovery and Climate Experiment)卫星通过主动测距方式获取的全球时变重力场被广泛用于全球大尺度陆地水储量变化研究(Tapley et al., 2004; Wahr et al., 2004).近年来,基于GRACE数据对长江流域内水资源及极端天气事件的研究也较多,例如Zhang等(2015)采用GRACE数据研究了长江流域干旱事件,并探索了陆地水异常与厄尔尼诺的可能联系;Zhang等(2016, 2019)利用GRACE数据对长江流域总体及子流域水文干旱分别进行了评估;Wang等(2020)提出了一种加权水储量亏损估计方法并结合GRACE数据来表征长江流域干旱事件.但GRACE数据主要存在以下局限:(1)受限于轨道与运行机制,其时空分辨率较低(时间分辨率为1月,空间分辨率~350 km);(2)高阶噪声与条带误差(Swenson and Wahr, 2006)需要进行滤波处理,进一步损耗和压制了原始信号;(3)数据质量不高并伴随着数据缺失,插值等后处理容易引入人为误差.这些因素导致GRACE卫星对高频和区域尺度的陆地水储量变化不敏感(Enzminger et al., 2018; Knappe et al., 2019),难以满足区域水资源管理利用、自然灾害防范的高时空分辨率需求(Feng et al., 2018).
全球定位系统(Global Positioning System)能够实时监测固体地球表面由于质量迁移产生的弹性形变,为实时监测陆地水储量变化提供了一种全新的解决方案(Argus et al., 2014; Xue et al., 2021).Farrell(1972)提出的质量负荷理论详细描述了负荷变迁与其造成的地表弹性变形之间的关系,目前根据质量负荷计算地表响应一般采用负荷格林函数法或球谐函数法(沈迎春等, 2017).鉴于无法获得全球性的(海洋及陆地)负荷位移,不能利用传统球谐函数将其转化至谱域内,大多数学者常用格林函数法对陆地水储量变化进行反演.例如,Argus等(2014)利用GPS位移数据结合负荷格林函数方法估算了美国西部的陆地水储量变化;Borsa等(2014)使用该方法研究了美国西部干旱期间的地下水流失量;Fu等(2015)计算了美国西北各州的陆地水储量异常;Johnson等(2017)利用GPS垂向形变时间序列来约束小地震断层面上每月的水文负荷和由此产生的应力变化模型,推断加州地震活动受水文循环的适度调节;Enzminger等(2018)则利用该反演模型估算了美国西部山区的雪水当量.利用GPS位移时间序列结合负荷格林函数方法能够获取50~100 km内天或天以下的负荷分布情况(Han and Razeghi, 2017),明显优于GRACE所能提供的时空分辨率.
相关学者试图采用Slepian函数法从谱域中获取大尺度的陆地水储量变化(Han and Razeghi, 2017; Jiang et al., 2021a; 成帅等, 2021).Slepian函数最早用于解决一维信号在时频域的最优集中问题(Slepian, 1964).为了解决大地测量学中存在的“极空白”问题,Sneeuw和Van Gelderen(1997)及Albertella等(1999)在球体上构建了一组新的Slepian基函数,使大部分能量最佳地集中在由整个地球减去极地间隙组成的纬向带内.在此基础上,Simons等(2006)又实现了球面空间任意区域的谱集中.后来的学者基于Slepian函数对冰盖质量变化进行了研究,例如Harig和Simons(2012)利用Slepian方法对GRACE球谐解进行谱集中,以此研究格陵兰岛质量时空变化;高春春等(2019)基于此提出了一种Slepian空域反演的方法,估算了南极冰盖子流域的质量变化.国内学者又将这一方法引入到重力场研究领域当中,陈石等(2017)利用其解算了中国大陆重力场的球谐模型;韩建成等(2021)基于地面重力观测建立了华北地区120阶的时变重力场模型.而Han和Razeghi(2017)利用Slepian基函数对GPS数据进行参数化和反演,获得了澳大利亚水文和大气质量的变化情况,使Slepian方法逐渐应用于陆地水储量反演;Jiang等(2021a)和成帅等(2021)采用同样的方法分别对中国地区与川云渝地区的陆地水储量变化进行了研究.
长江流域地域辽阔,地形起伏大,同时受东亚季风、印度季风影响,区域内降水时空分布不均,是旱涝灾害的多发地.近年来,全球变暖导致了水汽循环加速,降水的时空分布和强度受到了极大的影响(Cao et al., 2011),长江流域极端天气事件也随之增加.例如2010年发生特大洪水(Sun et al., 2017)、2011年春季出现严重干旱等(Zhang et al., 2015; Sun et al., 2018; Wang et al., 2020),这些自然灾害给当地水资源、农业、自然生态系统和社会造成了重大影响.因此,量化长江流域陆地水储量变化的时空分布特征将有助于理解区域内水文循环模式以及水文与气象相互作用的机制(Wang et al., 2020),对旱涝灾害的预防、水资源管理利用及区域可持续发展有着重要意义(Jiang et al., 2021a).
以上研究说明目前迫切需要掌握长江流域水储量变化及其时空格局,但关于利用GNSS研究长江流域陆地水储量变化还较少.因此,本文利用长江流域GNSS垂直坐标时间序列,采用Slepian函数法估计长江流域陆地水储量变化,并探索了流域内水储量变化的时空分布模式.将估算结果与其他大地测量和水文数据集进行对比分析,验证了长江流域水储量变化的时空分布特征,并量化了各子区域(金沙江流域、传统上游和长江中下游)不同数据集结果的相关程度和时间滞后关系,同时对反演模型的精度进行了评定.最后利用GNSS估计的水储量异常对极端天气事件进行追踪,并结合历史极端天气事件进行验证,为长江流域极端天气事件的监测提供了新的观测依据.
1 数据与处理
1.1 GNSS数据及处理
本文采用的GNSS时序产品从国家地震科学数据中心-东部形变数据服务中心(http:∥www.eqdsc.com)获取,该产品利用中国地壳运动观测网络(Crustal Movement Observation Network of China, CMONOC)获取的观测数据,采用麻省理工学院开发的GAMIT/GLOBK 10.40 (Herring et al., 2018)软件结合QOCA软件解算得到.本文选取了长江流域98个站点2011年1月—2020年12月单天解坐标时间序列,所选站点空间分布如图1所示.由于垂向位移对水文质量变化最为敏感(Dong et al., 2002; Kraner et al., 2018; Chanard et al., 2018; Panda et al., 2018),因此本文仅使用垂直位移进行反演建模.为了获取水文负荷位移变形,我们还需扣除其他非水文的影响因素,例如:线性的构造运动、非潮汐海洋与大气负荷变化(姜卫平等, 2014)、强震影响或仪器更新等引起的阶跃现象、以及热膨胀变形和冰后回弹效应等.原始GNSS垂直位移时序处理步骤如下:
(1)扣除非潮汐海洋与大气负荷位移:位移时序中包含的非潮汐海洋与大气负荷位移均采用德国地学研究中心(Geo Forschungs Zentrum, GFZ)提供的产品进行扣除(http:∥rz-vm115.gfz-potsdam.de:8080/repository)(Dill and Dobslaw, 2013).
(2)改正热膨胀变形:热膨胀效应对GNSS台站垂直位移的影响分为两部分,一是安装GNSS天线的水泥墩随温度变化热胀冷缩,另外地表温度变化传递到基岩也会引起GNSS台站发生垂向位移(闫昊明等, 2010; 姜卫平等, 2015).本文从中国气象局获取每日地表温度(http:∥data.cma.cn),并按闫昊明等(2010)提出的经验模型估算热膨胀变形,其中模型参数值采用贾路路等(2018)给出的相关参数.
(3)提取水文负荷形变:扣除上述因素引起的垂向位移后,将剩余的位移时间序列按公式(1)进行最小二乘拟合去除长期线性趋势、偏移量和震后变形(Jiang et al., 2017; 姜卫平等, 2018):
(1)
式中,y(ti)为ti时刻位置,y0为站点参考位置,v为线性项速率,Aj与Bj分别为周期项对应的振幅(j=1时为年信号,j=2时为半年信号),gk为阶跃项,Tk为阶跃发生的时刻,H为阶梯函数,ε(ti)为随机过程.
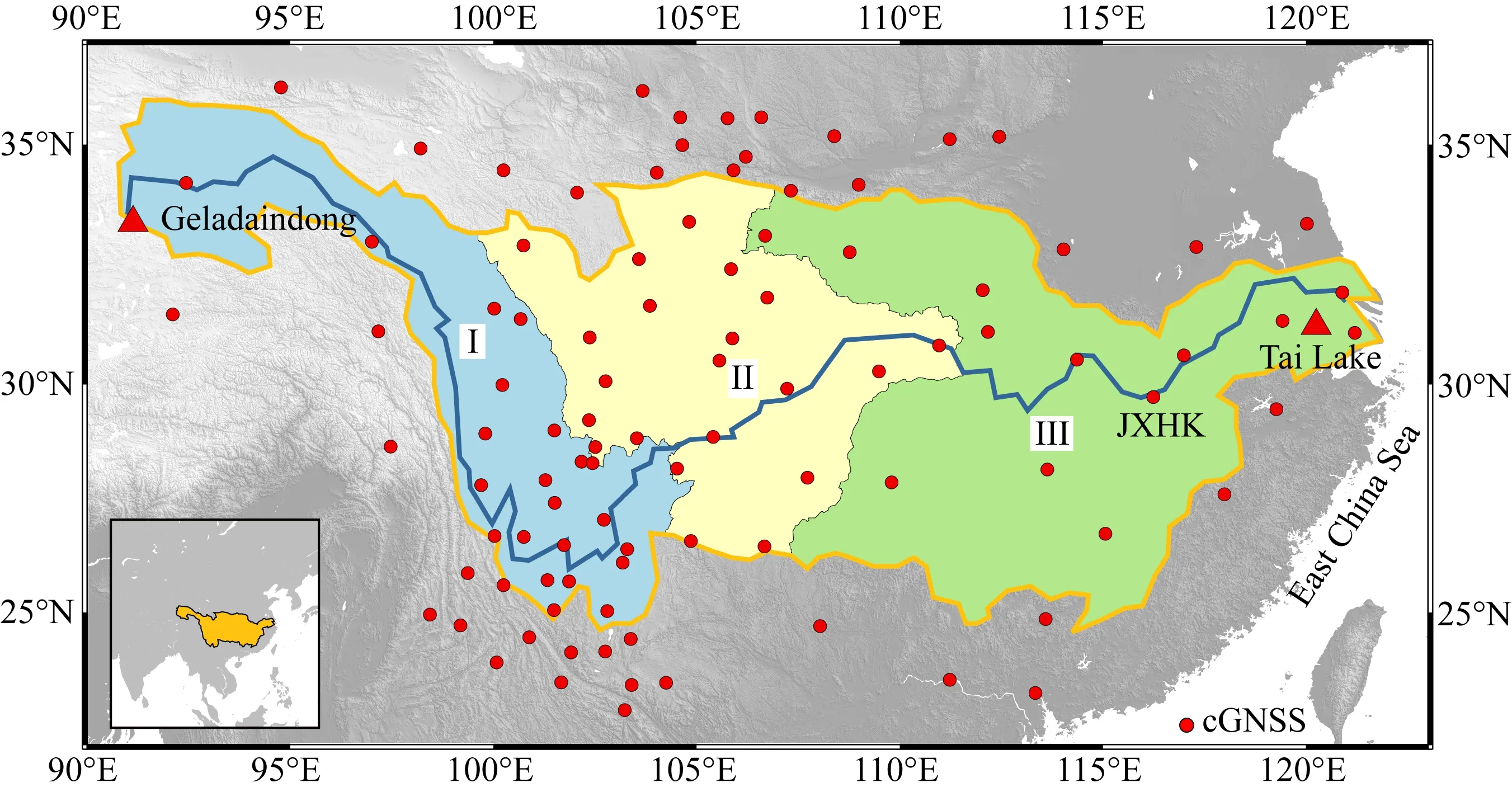
图1 GNSS站点分布及长江流域的地理范围蓝线为长江干流,黄线为长江流域边界,Ⅰ为金沙江流域,Ⅱ为传统上游地区,Ⅲ为长江中下游地区.Fig.1 GNSS station distribution and geographical range of the Yangtze River Basin Blue line represents the mainstream of the Yangtze River, and yellow line is the boundary of the Yangtze River Basin. Regions Ⅰ—Ⅲ are the Jinsha River Basin, the traditional upper reaches, and the middle and lower reaches of the Yangtze River Basin, respectively.
(4)补齐数据:本文获取的站点时间序列长度均在1000天以上,平均数据量达到3446天,占研究时间总长度的94%,具有较高的数据完整性.为保证具有相同采样率的连续时间序列进行时变反演,缺失的数据通过使用GMIS软件(GNSS Missing Data Interpolation Software)进行补齐(Liu et al., 2018).这种动态时空插值方法采用克里金-卡尔曼滤波(Kriging Kalman Filter, KKF),在处理基于网络坐标时间序列的连续和随机数据间断方面具有优异的性能.以部分站点为例,图2展示了JSYC、HNLY、QHBM、CQCS、SCLT、YNXP六个站点GNSS水文负荷位移时序经过补齐前后的结果.
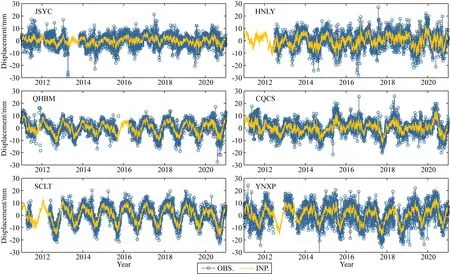
图2 GMIS软件对水文负荷位移时序进行补齐后的滤波结果OBS表示原始时间序列,INP表示补齐后的结果.Fig.2 The filtered results of hydrological loading displacement time series that filled by GMIS software OBS represents the original time series and INP represents the result after filling.
1.2 GRACE数据
本文采用的GRACE数据为德克萨斯大学空间研究中心(Center for Space Research, CSR)发布的RL06 Mascon完全校准模型第二版本(http:∥www2.csr.utexas.edu/grace/RL06_mascons.html),研究时段为2011年1月至2020年12月,期间共有31个月的数据缺失.本文未对GRACE与GRACE Follow-on的衔接空缺(11个月)进行处理,其余缺失的数据采用三次样条插值进行补齐,最后将数据重采样至0.5°×0.5°格网.该模型解直接通过GRACE卫星Level-1B数据进行解算,在时间和空间上采用先验信息进行约束,以减少南北条带误差和测量误差(Save et al., 2016),因此数据使用过程中不需要任何滤波或缩放因子,可以省略平滑或去条带的后处理过程.数据发布前修正了C20、C30项,并对一阶地心项进行了改正,同时扣除了冰后回弹效应以及非潮汐大气、海洋负荷.最后扣除了2004—2009年的平均值,直接发布陆地水储量的每月变化值.
1.3 水文数据
水文模型采用美国航天航空局提供的全球陆地数据同化模型(Global Land Data Assimilation System, GLDAS) Noah2.1同化数据(https:∥disc.gsfc.nasa.gov/datasets),数据以0.25°×0.25°的格网形式发布,时间分辨率为1个月.该模型依赖于多个陆地表面模型和气象驱动数据集的组合,综合了降水、太阳辐射、气温和其他气象因素的影响(Rodell et al., 2004),最终提供从地表到2 m深度的土壤水估计值、雪水当量和冠层水分量.本文对各水成分求和后经过去平均处理获得GLDAS水储量变化,同样将其重采样至0.5°×0.5°格网.
降水作为陆地水的来源,是直接影响陆地水储量变化的一个重要因素,因此本文结合中国气象局气象数据服务中心的逐月降水资料尝试探索降水量与陆地水储量变化的关系.该数据集整合了中国大陆均匀分布的2472个地面气象台站的降水资料,处理后经交叉验证对质量状况进行检验,最后通过薄板样条的空间插值方法给定中国大陆所有格网点的降水值,并以0.5°×0.5°的格网形式发布.
2 原理与方法
2.1 Slepian基函数
理想情况下,全球性的物理场量在谱域内具有无限带宽(Mitrovica et al., 1994;朱广彬等, 2012),以球谐函数作为基函数可以恢复球面上任意位置或任意空间尺度下的物理信号.由于参数估计的有限性,估计量具有带限特征,常用截断到某阶次的球谐位系数结合基函数来表征这个物理场量.在谱域内任意时变的球面信号σ(θ,λ,t)可近似表达为:
(2)
式中,a为地球半径,l,m分别为展开的阶数和次数,θ,λ分别为经度和余纬,cl m为l阶m次面球谐系数,Yl m为面球谐函数,L为带限宽度.
Slepian函数法能够构建既在全球又在感兴趣区域正交的一组带限基函数(Simons and Dahlen, 2006).对于局部而非全球的信号而言,用这组新的基函数的线性组合能够近似地表征该信号,使信号能量最佳地集中在研究区域内,物理场量σ可通过新的基函数表示为:
(3)
式中gα表示第α项Slepian基函数,cα表示第α项相应的Slepian系数.其中gα通过如下定义:
(4)
式中gα,l m表示第α项Slepian基函数的l阶m次膨胀系数,其本质是一组能将原始球谐函数转化为双正交(既在全球又在目标区域正交)的Slepian基函数的线性组合系数.膨胀系数的最优解则当基函数gα在给定封闭区域R内的能量与在整个地球Ω的能量之比达到最大值时取得,即:
(5)
式中,γα表示能量集中度(0≤γα≤1),γα趋近于1的基函数能量集中在R内,而趋近于0的基函数能量集中在R外.(5)式是Slepian问题在二维球面内的表达,引入核矩阵D对该问题进行求解:
(6)
Dgα,l m=γαgα,l m.
(7)
矩阵中每一项为各阶次两个球谐函数在区域R上的乘积积分,对D矩阵求解特征向量和特征值分别得到gα,l m与γα(式(7)).D矩阵的构建由区域R及带限阶数L共同确定,D矩阵确定的同时膨胀系数gα,l m及能量集中度γα被唯一确定,然后利用(4)式便可确定Slepian基函数.
图3a给出了Slepian基函数的能量空间分布,图中黄色实线表示长江流域边界,黑色虚线表示研究区扩充3°后的边界扩充线(Harig and Simons, 2012; 成帅等, 2021).由图3a可以看出,Slepian基函数能量通常从中心向外平滑扩散,但对边缘信号响应不敏感,边界扩充在一定程度上能够削弱这一影响.此外,站点水文负荷位移是站点附近区域内所有水文质量负荷变迁的综合体现,进行边界扩充可以更加准确地约束研究区边缘水文质量变化.

图3 基函数能量空间分布及能量集中度变化黄色实线为长江流域边界,黑色虚线为边界扩充线.α表示Slepian基函数按能量大小排序后的序号,γ表示能量集中度.Fig.3 Energy spatial distribution and energy concentration change of basis function Solid yellow line is the boundary of the Yangtze River Basin and dashed black line is the expansion line of the boundary. α represents the serial number of the Slepian basis function sorted by energy, and γ represents the degree of energy concentration.
通常情况下,加入运算的Slepian基函数个数由香农数N=(L+1)2A/4π确定.香农数作为局部谱优化的度量,定义为能量最佳集中在单位球上面积为A/4π的空间区域内最优基函数个数(Kennedy and Sadeghi, 2013; von Hippel and Harig, 2019).但在实际情况中,采用的基函数个数应小于GNSS站点数,否则求解Slepian系数会出现欠定情况,同时也要防止基函数太少和站点过多导致能量损失过多和模型过拟合的现象.本文采用的最大阶数为60阶,计算的香农数值为34,第34个基函数对应的能量集中度为0.51(如图3b).结合香农数与所选站点个数,并考虑保留足够的多余观测,最终选取前34个基函数对研究区域内水文信号进行恢复,其总能量恢复比例为87.8%.
2.2 反演原理
GNSS垂向位移时间序列经1.1节步骤处理后,将区域内GNSS站点垂直位移时间序列作为位移信号,结合(4)式求解的基函数并按(8)式通过最小二乘求解位移Slepian系数.
(8)
式中,d,n,J分别表示历元数、站点数和所选基函数个数,u表示水文负荷位移信号,Uα(td)为td时刻第α个位移Slepian系数,gi(θn,λn)为第n个站点第i个Slepian基函数.
根据质量负荷理论,质量负荷和地表响应可通过负荷勒夫数在谱域内进行线性转化(Farrell, 1972),负荷位移Slepian系数与陆地水储量Slepian系数在局部地区谱域内的转换关系如下:
(9)
式中,Sβ(t)表示陆地水储量Slepian系数,ρw表示水密度(1000 kg·m-3),ρe为地球平均密度(5517 kg·m-3),h′l为l阶垂向负荷勒夫数(Wang et al., 2012),两者的详细转化过程可参见Han和Razeghi (2017).
最后,将求解的陆地水储量Slepian系数利用Slepian基函数转化到空域内,并按能量集中度加权即可求解研究区域内陆地水储量变化.
(10)
3 结果与分析
3.1 垂向运动的周年变化
准确提取陆地水变迁引起的形变位移是有效约束区域内水储量变化的关键,本节对非潮汐海洋与大气负荷位移以及热膨胀变形的周年振幅进行了详细说明,并对水文负荷引起的地壳垂向季节性振荡进行了分析.非潮汐大气、海洋负荷位移以及热膨胀变形的周年振幅空间变化模式与地理区域具有很强的相关性.如图4a所示,青藏高原东部地区非潮汐大气负荷位移周年振幅为1~3 mm,四川盆地为3~4 mm,东部平原地区~5 mm.从沿海到内陆,非潮汐海洋负荷位移周年振幅表现出明显的递减趋势(图4b),近海站点的非潮汐海洋负荷位移周年振幅最高可达1.2 mm,但远海站点通常小于0.6 mm,空间分布特征与van Dam等(2012)的结果较为一致.热膨胀变形的周年振幅表现出更为复杂的分布模式,除海拔因素以外,与纬度也具有强相关性(图4c).总的来说,非潮汐大气、海洋负荷以及热膨胀效应引起的最大周年振幅分别可达5 mm、1.2 mm和1.2 mm,对站点垂向位移的贡献不容忽视.

图4 非潮汐大气负荷、非潮汐海洋负荷及热膨胀效应引起的垂向位移周年振幅站点颜色表示位移的周年振幅大小. (a)—(c)分别表示非潮汐大气负荷位移、非潮汐海洋负荷位移以及热膨胀变形的周年振幅.Fig.4 Annual amplitudes of vertical displacement caused by non-tidal atmosphere loading, non-tidal ocean loading, and thermal expansionThe color of site represents the annual amplitude of the displacement. (a)—(c) represent the annual amplitudes of non-tidal atmospheric loading displacement, non-tidal ocean loading displacement, and thermal expansion deformation, respectively.
为了验证提取的GNSS站点水文负荷位移的准确性,我们对GNSS及GRACE数据获取的负荷位移周年振幅进行了比较.图5展示了由全球Mascon模型解结合负荷格林函数正演得到的站点水文负荷位移的周年振幅GRACE-VCD(Vertical Crustal Deformation, VCD)以及提取的GNSS水文负荷位移周年振幅GNSS-VCD.从图5a与图5b可以看出,GNSS与GRACE获取的站点水文负荷位移周年振幅在空间分布上较为相似,但两者在量级上具有一定的差异.例如,西南地区GNSS-VCD普遍大于GRACE-VCD,其中GNSS-VCD最大可达9.7 mm,而GRACE-VCD仅有7.5 mm.此外,JXHK站点GNSS-VCD为8.3 mm,其附近站点GNSS-VCD也相对较大,但是在GRACE-VCD的分布中却没有体现.这可能与GRACE的低时空分辨率有关,另外,GNSS负荷位移时序中包含的其他未剔除干净的地球物理信号也可能会导致这一现象.图5c展示了GRACE-VCD与GNSS-VCD两组数据之间的相似性,散点坐标由各站点GNSS和GRACE获取的周年振幅确定.所有散点经过一次多项式拟合得到的直线斜率为0.54,其中68%的站点GNSS-VCD大于GRACE-VCD,这一结果说明在长江流域内GNSS获取的水文负荷位移大于GRACE,其原因可以分为两个方面.一方面,从GNSS时间序列中提取的水文负荷位移信号可能包含其他非水文信号的影响,例如交年项误差、非线性的地壳构造运动和观测噪声等.Fu等(2015)认为GNSS偏大的结果可能是因为交年项误差所引起,并指出交年项振幅占周年项振幅的平均比例为21.24%±13.56%;另一方面,由于空间分辨率的原因,GRACE Mascon模型解中仍然存在一定的泄漏误差,局部地区的Mascon结果不可避免会受到压制.

图5 GNSS与GRACE获取的站点水文负荷位移周年振幅及其比较Fig.5 Annual amplitudes of hydrological loading displacements obtained by GNSS and GRACE and their comparison
为进一步揭示GNSS垂向位移周年相位包含的信息,厘清长江流域在一周年内水储量变化的演变过程,本文结合降水的周年相位对GNSS站点反映的同期平均周年相位进行了讨论.图6展示的GNSS站点水文负荷变形的周年相位与降水周年相位具有相似的空间分布.从图6b可以看出,6月由于南北暖冷空气相遇,形成梅雨(Ye et al., 2019),长江中下游受梅雨影响率先达到降水峰值;随着亚洲夏季风的推进,其余地区相继在7月内达到降水峰值,云南地区气候主要受西南季风支配,降水峰值稍晚到达.图6a展示了周年内水文负荷引起的地壳垂向振荡首次达到低谷的时间(即水文负荷变化首次达到峰值的时间),相比降水周年相位有明显的延迟.结合GNSS周年相位分布情况,推测各区域水文负荷变化首次达到峰值的时间具有以下先后顺序:首先,6至7月长江中下游率先达到水文负荷变化峰值;结合降水周年相位结果,长江流域除中下游以外地区达到水文变化峰值的时间相近,但在8月中旬左右,GNSS结果显示青藏高原东边缘以上区域提前达到峰值,这可能是青藏高原东部冰川由于升温融化提供大量水分导致;最后,9月初至10月初,四川盆地及西南地区相继达到峰值(Jiang et al., 2021b),相较于降水晚2~3个月.

图6 水文负荷变形及降水在各GNSS台站的周年相位Fig.6 Annual phases of hydrological loading deformation and precipitation at GNSS stations
3.2 反演模型的不确定性
边界扩充是反演模型提升边缘信号响应、充分约束边缘信号的重要手段,本节对不同扩充边界的反演模型估算结果进行了讨论,并通过模拟实验对反演模型的截断误差进行了探究.将2011—2020年全球GRACE Mascon模型解作为模拟值,图7a展示了同期长江流域水文负荷变化周年振幅的空间分布.采用负荷格林函数方法获得98个站点的水文负荷位移时间序列,再使用Slepian函数方法结合不同扩充边界进行反演,恢复了不同缓冲区下的水文负荷变化信号(图7b—7f).由图7可见,扩充边界为0°或1°时,信号恢复的结果与模拟结果差异较大,且边界处信号响应不明显,而当扩充边界达到3°时,信号恢复结果趋于稳定.通过稳定的恢复结果与模拟结果对比,两者具有相似的空间分布,但西南边界处与长江中下游东部平原的恢复信号小于模拟信号,这可能与反演模型的截断误差有关,即选取基函数的过程类似于抑制高频信号,导致局部地区恢复结果更加平滑,造成区域内部的信号泄漏.实验结果表明,当扩充边界为3°时,研究区域内水文负荷变化能够得到有效约束,即300 km左右空间分辨率下3°以外质量负荷的影响几乎可以忽略,同时该模拟实验也验证了反演模型的有效性.
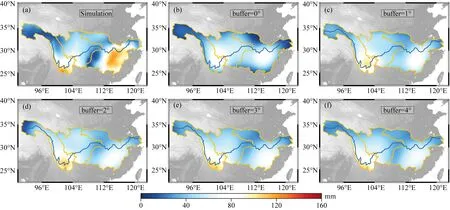
图7 不同边界扩充条件下的水储量变化空间分布Fig.7 Spatial distribution of water storage variation under different boundary extension conditions
利用Slepian基函数方法恢复区域尺度水储量变化过程中涉及到两次截断:第一次截断是由于Slepian基函数的带限特征所引起,本文选取的带限宽度为60阶,大于60阶的高频信号被舍弃;60阶Slepian展开应共有(60+1)2个基函数,根据香农数选取前34个基函数会造成第二次截断.为分析与评估截断误差对估算结果的影响,将提取的水文负荷位移u表示为两个分量(截断后的位移信号ures与截断误差δu1)(Han and Razeghi, 2017):
u(θ,λ,t)=ures(θ,λ,t)+δu1(θ,λ,t).
(11)
以2011—2020年全球GRACE Mascon模型解为例,首先利用负荷格林函数法计算站点水文负荷位移,站点位移时序RMS值(Root Mean Square)代表模拟值(图8a).然后利用站点位移时序获取的负荷位移Slepian系数结合Slepian基函数再次获取站点的水文负荷位移时序,模拟时采用3°扩充边界,截断误差用两次位移时序RMS变化量表示(图8b).从图8b可以看出,站点模拟值大小范围为1.5~5.5 mm,两次截断对站点位移信号的损耗最大~1 mm,其中93%的站点信号截断误差低于0.8 mm (边界范围内站点截断误差均小于0.8 mm),截断误差对站点位移的平均占比为8.1%,对位移信号影响较小.本文利用全球Mascon求解的水文负荷位移能够反映短波长和长波长的水文负荷总体变化情况,而西南地区及长江中下游的边界扩充范围内站点截断误差较大,结合上文边界扩充实验结果,分析其原因可能是反演模型对边缘信号不敏感(Harig and Simons, 2012)以及未考虑扩充边界外站点位移的约束,这也能部分说明边界扩充的必要性与有效性.就总体而言,反演模型在研究范围内对原始信号的削弱程度较小,证明该模型能够完成从离散位移信号到区域水文负荷的反演工作.

图8 站点位移的模拟值与站点位移的截断误差(a) 站点颜色表示站点位移时序的RMS值; (b) 站点颜色表示截断前后RMS变化值.Fig.8 Simulation value of station displacement and truncation error of station displacement(a) The color of station represents the RMS value of the station displacement time series; (b) The color of station represents the change of RMS before and after truncation.
3.3 水储量变化的空间模式
本文利用GNSS站点垂向位移时间序列,首先反演出各历元的长江流域水储量变化,再对得到的各格网点水储量变化时序进行拟合后获得格网点的水储量变化周年振幅大小,所有水储量变化周年振幅均用等效水高(Equivalent Water Height, EWH)表示.图9a反映了基于GNSS的长江流域陆地水储量变化的周年振幅空间分布.从总体上看,长江流域水储量变化在金沙江流域及长江中下游东部平原较大,在太湖及长江流域中部较小.其中金沙江流域陆地水储量变化最为明显,区域内GNSS-EWH最大周年振幅可达~214 mm,并呈现由西南向东北逐渐减小的趋势.这一现象可能原因有两个:(1)西南地区气候受亚洲夏季风支配,湿季(5—10月)降水丰沛,为流域内补充了大量水分;(2)西南地区植被覆盖度高,河流众多,有利于夏季水的存储.GRACE-EWH(图9b)与GLDAS-EWH(图9c)结果与GNSS-EWH有较为一致的空间分布特征,三者在金沙江流域变化显著,且GNSS-EWH与GRACE-EWH在长江中下游表现出较大的变化.降水作为陆地水存储的主要来源,降水量变化在一定程度上能够作为陆地水储量变化的依据,如图9d所示,长江流域多年平均降水量呈现由东至西逐步递减的趋势.但GLDAS在长江中下游的陆地水储量变化不明显,区域内最大周年振幅~60 mm,远小于GNSS-EWH的~143 mm及GRACE-EWH的~120 mm.长江中下游众多支流为地表水的存储提供了条件,因此这种差异很可能是由于GLDAS模型未对地表水成分进行建模所引起(Scanlon et al., 2018).太湖地处亚热带季风气候区,丰富的降水为其补充了大量水分,但由于气候与所处地理位置的影响,区域内蒸散、径流量相对较大,水储量收支较为平衡,这可能是太湖区域陆地水储量变化较小的原因.

图9 长江流域水储量变化周年振幅空间分布(a),(b),(c)分别表示基于GNSS、GRACE、GLDAS的周年振幅,(d)表示多年平均降水量.Fig.9 Spatial distribution of annual amplitude of water storage change in the Yangtze River Basin(a), (b), and (c) represent the annual amplitudes based on GNSS, GRACE, and GLDAS, respectively. (d) represents the multiyear mean precipitation.
图10展示了各数据集在长江流域及其子区域按纬度加权平均后的水储量变化时间序列,其中GNSS-EWH被重新采样成每月的结果,以便与其他数据集进行比较.基于GNSS的子区域平均水储量变化量级仍与水储量变化空间分布相匹配,金沙江流域平均水储量变化量级最大,传统上游与中下游相当.其中金沙江流域平均水储量变化时序周年振幅可达137 mm,分别是中下游的2.3倍、传统上游的1.9倍. GRACE-EWH在金沙江流域明显小于GNSS-EWH的结果,主要可能与GNSS水文负荷位移时序中包含的其他未剔除的信号有关;其次,GRACE低空间分辨率导致的信号泄漏与衰减(Chen et al., 2006)也可能存在一定的影响.GNSS-EWH与GRACE-EWH展示了所有水成分的整体变化情况,而GLDAS模型不包括深部地下水和地表水(河流、湖泊等)成分,在水系较多、径流量大的长江流域,与前两者结果相比水储量变化必然会被低估.GNSS垂向位移不仅记录了区域内水文负荷变化,而且对局部质量变化具有很高的敏感性(Knappe et al., 2019),由GNSS约束的结果能够反映更为精细的水文负荷效应(王伟等, 2017),考虑采样频率、建模方法及观测手段等因素,几种数据集结果可能会存在一定的差异.
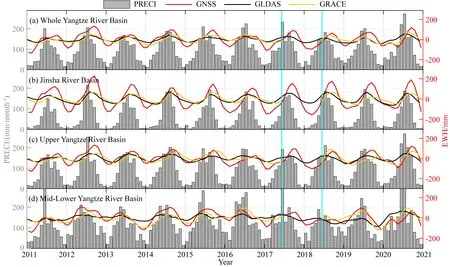
图10 长江流域及其子区域水储量变化时间序列(a), (b), (c), (d)分别表示整个长江流域以及金沙江流域、传统上游、长江中下游的区域水储量变化时间序列.青色线之间表示GRACE与GRACE-FO的衔接时段.Fig.10 Time series of water storage change in the Yangtze River Basin and its sub-regions(a), (b), (c), and (d) represent the time series of regional water storage change in the whole Yangtze River Basin,the Jinsha River Basin, the traditional upper reaches, and the middle and lower reaches of the Yangtze River. Cyan lines represent the transitional period of GRACE and GRACE-FO.
3.4 时变水储量变化与极端事件
为了深入研究季节性水储量变化的时间特征,本节对长江流域及其子区域2011年1月—2020年12月间的水储量变化时序进行了分析,量化了地表降水与水储量变化的时间相关性和时滞特征,并对GNSS探测流域尺度极端降水事件的能力进行了验证.
从图10a可以看出,GNSS-EWH能够表征长江流域水储量变化的季节性,与月降水量的相关性较好(CC=0.59),但两者存在明显的相位滞后关系.各数据集的互相关系数及滞后月数在表1中列出,表中大部分互相关系数通过了Monte Carlo模拟一阶自回归时间序列(AR1)置信度为95%的显著性检验(高春春等, 2019).其中,GNSS-GRACE、GNSS-GLDAS、GNSS-PRECI、GRACE-GLDAS、GRACE-PRECI以及GLDAS-PRECI的置信水平值分别为0.45、0.45、0.46、0.46、0.48和0.47.GNSS-EWH出现峰值的时间较降水峰值出现时间平均晚2~3个月,在亚马逊盆地等热带地区也出现了相同的现象(Humphrey et al., 2016),Hsu等(2020)认为这种现象与水资源储存和运输的复杂动态过程有关.需要指出的是,水储量与降水量作为不同的物理量(二者为微分关系),探索两者之间的定量关系还需进行后续的数据处理.对比子流域的时间序列结果(图10b—d),GNSS-EWH与其他数据集相关系数均大于0.48,在金沙江流域GNSS-EWH与GLDAS-EWH的相关系数可达0.84,说明GNSS-EWH反映的流域水储量变化情况与其他数据集反映的水文情况具有较强的一致性.在金沙江流域与传统上游,GNSS-EWH出现峰值时间比降水出现峰值时间晚2个月,而长江中下游的时间滞后不明显(小于1个月),达到峰值时间普遍早于上游与金沙江,推测可能是由于梅雨天气与局部空间变异所导致,整个长江流域的时滞性特征主要由金沙江流域与传统上游贡献.

表1 长江流域及其子区域不同数据集之间的相关系数与滞后月数Table 1 Correlation coefficients and lag months between different datasets in the Yangtze River Basin and its sub-regions
长江中下游作为我国水资源配置的战略水源地,区域内人口密集、工业发达,但极端水文事件常有发生,因此本文以长江中下游极端事件为例进行研究.图11b展示了基于GNSS-EWH计算的长江中下游10年间的水储量盈亏情况,其中,水储量盈亏通过图11a展示的水储量变化估计值与气候学值(参考值)的差值产生.统计发现,长江中下游在2012、2014—2016年均发生了水储量盈余的现象,而在2011、2013、2018年水储量发生亏损,这些结果与Zhang等(2015)、Ma等(2018)、陈威等(2020)、Jiang等(2021a)的描述相符.除地形、气候与人为(Chao et al., 2021)等因素外,相关资料显示2011年春季长江中下游的水储量亏损可能是由于La Nia现象导致的干旱造成(Zhang et al., 2015),2015—2016年水储量盈余的现象也与该时期发生超强El Nio有关(陈威等, 2020; Ma et al., 2018).图11c中展示的降水异常与GNSS估算的水储量盈亏情况较为吻合,两者互相关系数为0.49,说明长江中下游水储量变化在一定程度上受降水驱使,该区域极端事件的发生往往与降水量联系紧密,且降水异常的反馈在陆地水储量异常结果中会延迟显示.通常情况下,实测降水不足以描述极端水文事件(Famiglietti and Rodell, 2013),而扣除了大气和非潮汐负荷等影响后,GNSS负荷垂直位移估算结果是所有水成分变化的综合体现,可独立表征水文极端情况,无需附加其他观测约束.总的来说,连续运行GNSS网络即使在稀疏的空间覆盖下,也可以作为识别和量化水文极端情况的补充工具.

图11 长江中下游水储量盈亏情况及区域内降水异常Fig.11 Water storage surpluses and deficits in the Yangtze River Basin′s middle and lower reaches, as well as precipitation anomalies in this region
4 结论
本文基于稀疏的GNSS台站网络数据,结合Slepian基函数获取长江流域GNSS网位移的局部谱,并利用质量负荷理论实现从负荷位移的空间变化到水储量的空间变化的转化,得到了长江流域及其子区域的水储量变化.通过模拟实验,对反演模型的不确定性进行了评估,验证了反演模型的有效性.将GNSS估算结果与GRACE、GLDAS及气象降水三个数据集进行对比,讨论分析了长江流域及其子区域水储量变化的时空分布模式,展示了GNSS独立监测极端水文事件的能力.研究结果表明:
(1)站点水文负荷位移与其推算的水文负荷分布较为吻合,在西南地区与江西湖口站(JXHK)水文负荷位移周年振幅较大,相对应的水储量变化在该站点附近也较为显著.此外,利用该反演模型对长江流域水储量进行约束,当边界扩充为3°时能够获得稳定的结果,在此条件下,反演模型造成的截断误差对原始位移信号影响较小.本文将Mascon模型解计算的位移作为模拟值,估算出的截断误差量级~1 mm,其中边界范围内站点截断误差均小于0.8 mm,截断误差对站点位移的平均占比仅为8.1%.
(2)多种数据集的结果在空间上表现出一致的分布情况,GNSS结果与GLDAS、GRACE空间相关度分别为91%和79%.具体表现在:西南地区降水丰沛、持水能力强,在金沙江流域水储量变化周年振幅最大,并呈现西南向东北递减的趋势;长江中下游水系复杂,且受梅雨天气与亚洲夏季风影响,中下游东部平原局部变化也较为明显.由于GNSS位移在包含了更为细节的局部质量空间分布的同时也可能包含了其他非线性地球物理信号,而GRACE存在信号泄漏、GLDAS存在建模不完整的问题,几种数据集的结果也存在一定的差异.GNSS估算的长江流域水储量变化显著,其最大周年振幅可达~214 mm,分别是GRACE-EWH最大周年振幅的1.8倍、GLDAS-EWH最大周年振幅的2倍.
(3)不同数据集在长江流域及其子区域水储量变化均表现出明显的季节变化与年际变化.GNSS与GLDAS、GRACE的时序相关系数均在0.56~0.84之间,在金沙江流域和传统上游,GNSS结果较降水出现峰值的时间晚2月左右,而在长江中下游地区几乎没有时延现象(时间滞后小于1个月).利用GNSS能够监测到降水异常的情况,且对GNSS反演结果水储量变化异常情况统计发现,长江中下游在2012、2014—2016年均发生了水储量盈余的现象,在2011、2013、2018年水储量发生亏损,这些结果在相关文献中有相应的报道,证明GNSS具有独立监测极端水文事件的能力.
GNSS反演结果与多源数据集一致的时空特征验证了Slepian函数法反演陆地水储量变化的可靠性,这也为多源数据融合提供了一种新的思路.同时,基于GNSS的反演结果能够反映所有水成分整体的变化或异常情况,这也为区域干旱、洪水的量化研究提供了新的数据集.而Slepian函数法作为一种局部谱集中的方法,密集的地面观测能够更加充分地约束地表负荷的变化,增加站点覆盖仍然是提升反演结果空间分辨率、获取更加精细水储量变化空间分布特征的重要手段.
致谢感谢三位审稿专家的宝贵建议.感谢国家地震科学数据中心-东部形变数据服务中心提供的GNSS坐标精密时序,感谢中国气象局提供的降水与地表温度数据以及德克萨斯大学空间研究中心(Center for Space Research, CSR)、德国地学研究中心(Geo Forschungs Zentrum, GFZ)提供的相关数据产品.并衷心感谢美国普林斯顿大学Simons教授提供的Slepian相关源码和耐心解答以及南阳师范学院高春春副教授给予的指导.

