极区电离层闪烁指数和对流速度关系的建模研究

陆盛, 邢赞扬*, 邓忠新, 张清和, 王勇,王成, 冯健, 马羽璋, 夏凯

1 山东大学空间科学研究院山东省光学天文与日地空间环境重点实验室, 山东威海 264209 2 中国电波传播研究所电波环境特性及模化技术重点实验室， 山东青岛 266107 3 中国空间技术研究院钱学森空间技术实验室, 北京 100101 4 中国电波传播研究所， 山东青岛 266107

0 引言

当无线电信号穿过电离层时，其幅度、相位等信息会在电离层电子密度不均匀体的作用下产生随机扰动，即电离层闪烁.电离层闪烁一般由相位闪烁指数σφ和幅度闪烁指数S4来描述，指数越大表示信号发生的闪烁越强.电离层闪烁与人们的生活息息相关，尤其对广泛使用的卫星导航定位系统有着不可避免的影响.卫星导航系统是一个弱信号系统，电离层闪烁会严重影响其各类地面接收终端的正常工作，明显降低导航和通信的可靠性和精度，严重时甚至会导致星地传输信号中断，造成卫星失锁.因此开展电离层闪烁现象的理论与观测特征研究，对保障卫星导航和通信等系统的可靠运行有着重要意义.

大量研究表明，地球磁赤道附近和高纬极区是电离层闪烁的多发区.而相比于磁赤道附近，高纬极区电离层闪烁具有更为复杂的气候/物理特征，目前还缺乏一种有效理论来解释其形成机制及其效应的影响，故本文将重点研究极区电离层闪烁现象.在这一区域，大多数无线电波信号闪烁都是在穿越高度范围200～1200 km的F层电离层不均匀体时产生的(Aarons,1982;Aarons et al.,1984).

在20世纪初，国际上就已开始广泛开展电离层闪烁现象的相关研究，建立了数量密集、分布较广的监测网.基于庞大的闪烁观测数据，科学家们发现了电离层闪烁现象的许多特性并尝试建立闪烁模型.Priyadarshi(2015)广泛总结了前人的研究成果，将闪烁模型分为分析模型、全球气候模型和基于原位数据的模型三类，确立了整个闪烁建模研究的框架.但在高纬度极区，恶劣的自然环境使得地面接收站稀少，使得极区电离层闪烁的观测数据十分匮乏，从而导致目前大多数电离层闪烁模型在高纬地区不适用或无法验证有效性.比如：Fremouw和Rino(1973)提出的弱散射条件下电离层闪烁理论是第一个闪烁分析模型，其基于理论假设提出了闪烁发生的一种可能机制，具有很好的发展潜力，但目前只在具有丰富VHF(Very High Frequency)频段观测的低纬赤道地区得到了验证(Carrano et al.,2016)；WBMOD(Wide Band Model)和GISM(Global Ionospheric Scintillation Model)等全球气候学闪烁模型，主要用于描述全球范围内闪烁的大尺度分布特征，但此类模型已被证实在高纬地区和极端空间天气状况下会产生较大误差(潘丽静,2015)；基于原位数据的模型则是一种以卫星观测数据为基础的半经验或者纯经验模型，可以相对准确地模拟和预测一个数据丰富地区的闪烁情况，而很难模拟台站稀少、数据相对匮乏的高纬地区.

目前，虽然高纬地区闪烁的研究较少，但已有的一些研究发现可以有助于我们了解极区电离层闪烁的统计特征和影响因素.如：Coker等(2004)指出高纬地区的闪烁主要由电离层F层密度梯度不均匀体引起；MacDougall和Jayachandran等(2001)指出高纬度地区发生闪烁时的电离层对流速度非常大且变化十分迅速(100～1500 m·s-1)；王勇等(2018)基于磁正午附近GISTM(GNSS Ionospheric Scintillation and TEC Monitors)台站的闪烁观测与SuperDARN(Super Dual Auroral Radar Network)雷达的对流速度观测，发现电离层对流速度与相位闪烁指数σφ存在明显的线性关系，而与幅度闪烁指数S4的关系并不明显.这些研究表明极区电离层相位闪烁指数与电离层对流速度存在重要联系，为本文将弱散射条件下电离层闪烁理论应用于高纬极区，建立极区电离层闪烁指数与对流速度的理论关系式的工作提供了研究基础.

本文首先回顾了弱散射条件下电离层闪烁理论以及Carrano等(2016)对该理论的改进和优化，并在此基础上推导出对流速度与σφ/S4的显式关系式.随后利用该关系式计算了加拿大Hall Beach台站附近闪烁所伴随的电离层对流速度，并将计算结果与SuperDARN雷达在该地区实测的对流速度进行比较验证，评估了由该方法获得对流速度的准确性.最后，根据本文提出的闪烁事件选取标准，挑选出2015年发生在Hall Beach地区的8个闪烁事件，并利用这些闪烁事件期间的地面实测数据，进一步验证了本文建立的对流速度与σφ/S4显式关系的可靠性.该理论关系将会提供一种获取极区电离层对流速度的新渠道，具有着重要的应用价值与发展前景.

1 原理与方法

1.1 弱散射条件下的电离层闪烁理论

基于弱散射条件的电离层闪烁理论由Fremouw和Rino(1977)首次提出.理论的中心思想是将电离层看作一个薄层，并假设卫星发出的信号只在距地面350 km的F层电离层穿刺点处发生单次散射，信号的单次散射由一阶玻恩近似进行展开.随后，基于相位屏理论和冷等离子体近似等假设， Rino(1979)推导出了较为简洁的闪烁指数表达式，但由于表达式中所含的电子密度扰动项无法被精准测量，所以计算出的闪烁指数会存在较大误差.最近，Carrano等(2016)对该理论做了进一步优化.他们发现两个闪烁指数表达式中都包含共同项(Cp)，通过将闪烁指数做比即可消除表达式中难以测量的电子密度扰动项，而未被消除的项中包含的有效扫描速度(Veff)又与电离层对流速度(VD)密切相关.基于此，他们开发了一种由单站GNSS(Global Navigation Satellite System)测量的闪烁指数来推断电离层对流速度的方法，并在低纬地区的三个台站进行了简单的验证，但尚未在高纬地区进行应用验证和适用性分析.

本节将首先简单回顾上述三篇文章对弱散射条件下电离层闪烁理论的改进优化，然后在此基础上进一步给出电离层对流速度与闪烁指数比值σφ/S4的显式关系方程，最后通过给出符合高纬地区的模型参数，将该理论应用于高纬极区.

1.2 基于平面波场单次散射的闪烁指数理论表达式

在本节中，我们主要描述以下形式平面波场的单次散射：

E(r)=Au(r)exp(-ik·r).

(1)

任意波场穿过电离层不均匀体时发生的弱散射可近似为波矢为k和电场矢量为E的入射平面波在假设散射高度处发生的单次散射，散射的几何位型如图1所示.图1中xyz坐标系的原点位置称为电离层穿刺点(Ionospheric pierce point，IPP)，即当假定电离层是一个厚度为h的薄壳时， 卫星和接收机的连线与电离层的交点.此外，坐标系x轴正方向为地理正东方向，y轴正方向为地理正南方向，π/2-θ和φ分别为穿刺点相对于地面接收机的仰角与方位角，r为传播信号相对于坐标原点的位矢.对于较小的散射角θs(平面波振幅矢量A与散射波电场矢量E1的夹角)，Rino(1977)采用一阶Born近似得到散射波方程：

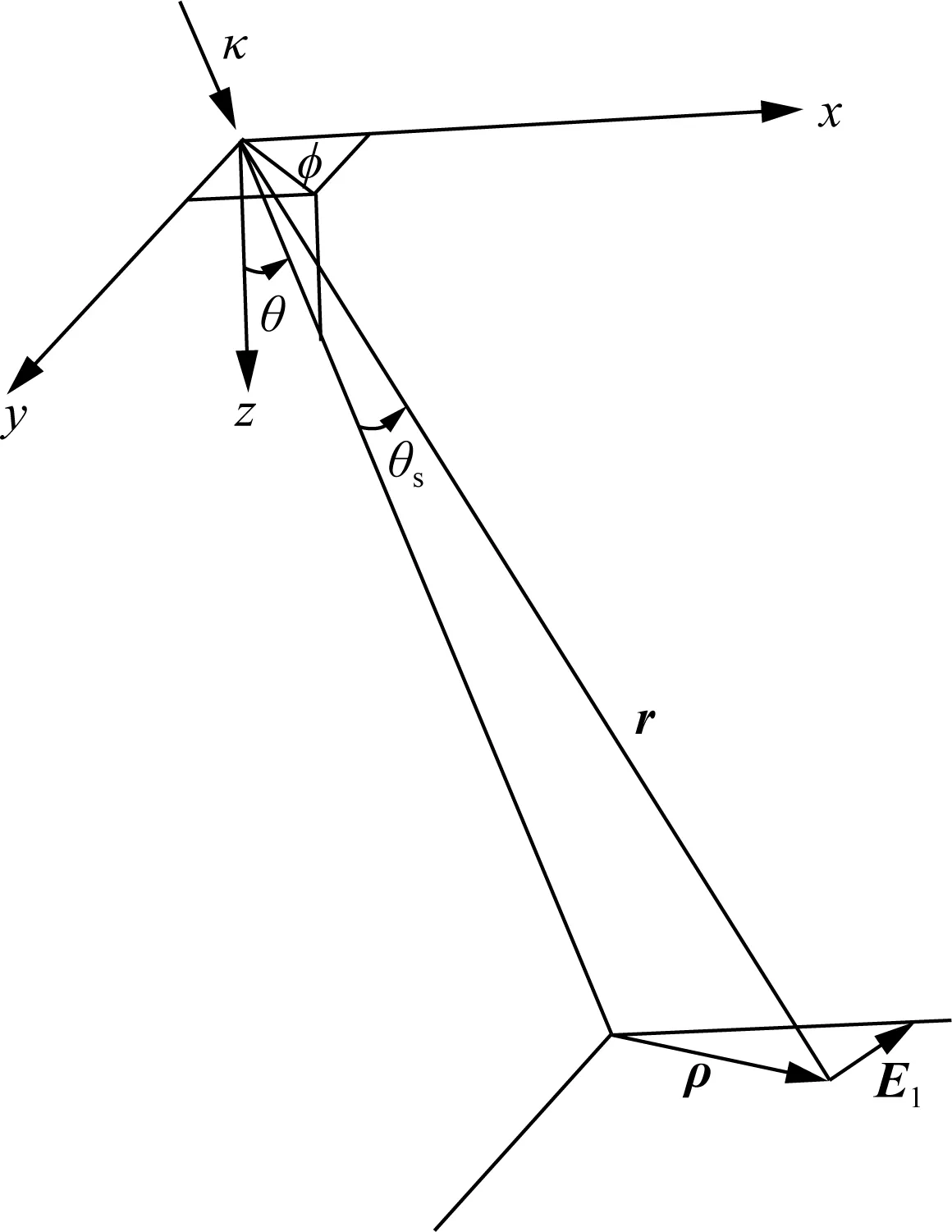
图1 电离层闪烁的一阶波恩近似的几何位型x,y,z轴分别指向地理东,地理南和地心方向，κ为信号入射方向，π/2-θ和φ分别为穿刺点相对于地面接收机的仰角与方位角，θs为散射角，r为散射信号相对于坐标原点的位矢，ρ散射信号相对于原入射波方向的位矢，E1为散射波电场矢量(Fremouw and Rino,1977).Fig.1 Geometry for first-order Born approximation scatting The x, y, and z axes point to the geographic east, geographic south, and geocentric directions, respectively; κ is the signal incident direction; π/2-θ and φ are the elevation and azimuth angles of IPP relative to the ground-based receiver, respectively; θsis the scattering angle, r is the potential vector of the scattered signal relative to IPP; ρ is the potential vector of the scattered signal relative to the direction of the original incident wave; E1 is the electric field vector of the scattered wave (from Fremouw and Rino,1977).

(2)

其中

×exp[(-ik·(r′-r))]G(r,r′)dr′,

(3)

(4)

假设引起散射的不均匀体为长轴沿地磁场方向的椭圆形，那么在地磁场坐标系(r,s,t)中等离子体密度扰动的自相关函数应有较为简单的形式(Singleton et al.1970):

(5)

其中a∶b代表不均匀体椭圆的轴比.为了在之前的分析中使用，需要在地理坐标系(x,y,z)中描述RΔNe.当a∶b大于1时，不均匀体的长轴和短轴方向分别沿s轴和t轴，此时坐标变换方程为

s=xcosψ+zsinψ,

t=xsinψsinδ+ycosδ-zcosψsinδ,

r=xsinψcosδ+ysinδ+zcosψcosδ,

(6)

其中ψ是磁倾角，δ是磁偏角.通过坐标变换和傅里叶变换，不均匀体密度扰动自相关函数可写为Fremouw和Rino(1977)中的(40)和(42)式.Rino(1979)从这两式出发分别推导出相位闪烁指数σφ和幅度闪烁指数S4表达式.最近，Carrano 等(2016)对Rino(1979)文章中两个闪烁指数的表达式进行了改写(相位闪烁指数实际上求的是其均方根相位)：

(7)

(8)

其中

(9)

(10)

(11)

(12)

(14)

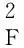
(15)

其中，p是相位谱指数(phase spectral index)，ν=0.5p;2F1是高斯超几何函数.(13)、(14)式中出现的A、B、C等系数取决于信号传播方向与不均匀体轴的夹角.由于公式(7)、(8)中包含的电子密度扰动项难以被精确测量，所以由其计算出的闪烁指数与闪烁仪实际测量的结果相比会存在较大偏差(Fremouw and Rino,1977).

1.3 电离层对流速度VD与σφ/S4的线性关系推导

(16)

上式中，第一个中括号中的项仅是相位谱指数p的函数，第二个和第三个中括号中的项只取决于信号传播方向与卫星扫描运动情况.若已知σφ和S4的测量结果，则可以由(16)式反解出卫星有效扫描速度：

(17)

Rino(1979)给出卫星有效扫描速度与对流速度关系的一般表达式：

(18)

在上式中，Vsx和Vsy是对流速度相对于IPP处的磁北向和磁东向分量.忽略对流速度可能的北向和垂直分量(即假设电离层对流速度只沿地磁纬向)，由伽利略速度变换可得：

Vsx=-Vsx0,

Vsy=VD-Vsy0,

(19)

Vsx0=Vpx-tan(θ)cos(φ)Vpz,

Vsy0=Vpy-tan(θ)sin(φ)Vpz,

(20)

其中Vsx0和Vsy0是对流速度相对于IPP处的射线路径速度的磁北向，磁东向分量；Vpx、Vpy和Vpz分别是IPP处的射线路径速度的磁北向、磁东向和垂直方向分量.在Wang等(2019)的计算中,对于在高纬度地区上空的GPS卫星 L1波段的信号，当假定接收机到相位屏的距离为350 km并且忽略垂直方向的速度时，卫星穿刺点在这一高度处的典型运动速度为Vpx(～60°elv)≈80 m·s-1；Vpy(～60°elv)≈10～20 m·s-1.

将(19)、(20)式代入(18)式，解一元二次方程后可建立对流速度VD与有效扫描速度Veff的关系式：

(21)

其中VD0=Vsy0-B·Vsx0/A表示最小对流速度的大小，故上式中应只保留符号为‘+’时的解.将(17)代入(21)式并让相位谱指数p=3即可得到对流速度VD与闪烁指数比值的显式关系:

(22)

下面将对该式中的参数重新进行假设，以验证由闪烁指数来反演电离层对流速度的方法是否适用于极区电离层.上述模型需要输入的参数包括电离层假设参数、接收站信息以及卫星信号信息三部分.电离层假设参数具体如下：假设在高纬度区域闪烁信号的相位谱指数p=3；假设散射高度为350 km；在低纬地区的不均匀体椭圆的长轴方向大致沿赤道方向，Carrano等(2016)的研究表明轴比可以设为a∶b=10∶1或者设为无限轴比都可以较好地贴近真实的测量结果，而在高纬地区，长轴方向沿纬线方向，一般认为轴比应设为1∶10.接收站信息主要包括接收机所在经纬度以及对应的磁倾角和磁偏角等参数.卫星信号信息包括GPS接收机实时提供的σφ和S4指数，卫星仰角和方位角等信息.

2 数据与仪器

2.1 闪烁指数的统计定义

幅度闪烁指数S4和相位闪烁指数σφ是表征电离层闪烁强度的两个重要指标，它们分别表征接收信号相比卫星出射信号在振幅和相位上产生的变化.前者的统计定义为每分钟内信号强度的标准差除以接收功率的平均值，而后者则是由在固定扰动频率间隔上一个周期内的载波相位标准差来描述.两个闪烁指数的统计表达式如下：

(23)

(24)

其中〈SI〉表示一个周期内信号强度的平均值，φ表示载波信号的相位.为了减少闪烁指数的测量值误差，接收到的卫星信号通常需要剔除由卫星相对于地面接收机的实时相对运动、多路径效应等引起的噪声，一般舍弃S4<0.05以及σφ<0.05的数据，认为它们是接收机的噪声.此外，根据Van Dierendonck(1993)的研究，使用数据中的S4cor参数来校正S4指数可以有效消除由热噪声引起的误差.

2.2 加拿大高纬度北极电离层监测网络(CHAIN)

加拿大高纬度北极电离层监测网(Canadian High Arctic Ionospheric Network)是分布在加拿大高纬度北极地区的地面无线电仪器阵列，共有35个台站，配备的仪器包括25个高数据率全球导航卫星系统电离层闪烁和总电子含量监测器(GNSS Ionospheric Scintillation and TEC Monitor, GISTM)和6个测高仪(Canadian Advanced Digital Ionosonde, CADI).Hall Beach台站作为为数不多同时装备GISTM和CADI的台站可提供建模所需的卫星信息和穿过电离层信号的信息.

Hall Beach台站配备的闪烁监测仪型号为NovAtel GSV4004B，这种链式接收器可同时接收视野范围内多颗GPS卫星发送的卫星轨道数据和信号闪烁数据.该种接收器可在L1(1575.42 MHz)和L2(1227.6 MHz)频段以50 Hz的数据频率对每颗卫星信号的相位和振幅进行实时跟踪测量，并根据测量结果计算出总电子含量(TEC)、幅度闪烁指数和相位闪烁指数等与电离层状态相关的参量.为了减少由地面物体的多径反射造成的测量误差，通常使用60 s分辨率的闪烁数据，并舍弃卫星仰角低于20°的数据.

2.3 超级双子极光雷达网络(SuperDARN)

超级双子极光雷达网络(SuperDARN)是一个国际性的雷达网络，由30多部低功率高频雷达组成，主要用于研究大气层的高层以及电离层.Rankin Inlet(RKN)雷达是其中一部位于高纬度地区的雷达，可在HF(High Frequency)频段利用多普勒效应测量电离层电子密度不均匀体的对流速度.SuperDARN雷达发射信号的方向并不是垂直向上而是以一定的倾角斜射入天空，在标准模式工作下，该雷达可在16～24个Beam上扫描，扫描的总扇区为50°或80°，每个Beam约为3.3°，扫描周期为1或2 min.每个扫描光束的有效测量距离超过3000 km，这段距离被划分为75个长度为45 km的测距门.Hall Beach台站(68.77°N，278.74°E)位于RKN雷达(62.82°N，266.89°E)Beam 15的一个测距门内(图2).

图2 位于Rankin Inlet (RKN)的SuperDARN雷达的Beam 15可以覆盖Hall Beach上空(60°、70°、80°代表地理纬度)Fig.2 Beam 15 of the SuperDARN radar at Rankin Inlet (RKN) covers Hall Beach ( 60°， 70°， 80° represent geographic latitude)

3 极区闪烁指数与对流速度关系的验证

3.1 极区电离层闪烁典型事件分析

由于电离层闪烁现象多发于磁暴期间，通过处理分析2015年磁暴(SYM-H指数小于-50 nT)期间Hall Beach台站的闪烁实测数据以及该地区上空的SuperDARN雷达的对流速度实测数据，我们发现了一个发生于2015年9月9日20∶00—22∶00 UT的典型闪烁事件.在这一段时间内，一颗编号为G2的GPS卫星刚好穿越Hall Beach台站上空，并且相对于台站有一个很大的仰角(图3)，可以有效避免多路径效应对信号的干扰.图4显示在该时间段内位于Rankin Inlet (RKN)的雷达有较强的回波信号，测量到的电离层对流速度(记为SDVD，单位m·s-1)展示在图5中.

图3 G2卫星相对于Hall Beach(halc)台站的方位角与仰角图(黑框区域为21∶00—22∶00UT内IPP轨迹)Fig.3 Azimuth and elevation map of the G2 satellite relative to the Hall Beach (halc) station (the black box area is the IPP track from 21∶00 to 22∶00UT)

图4 位于Rankin Inlet (RKN)的SuperDARN雷达在2015年9月9日20∶00—22∶00 UT间在Hall Beach台站上空有较强的回波信号(红色圆点为Hall Beach位置； 60°、70°、80°代表地理纬度)Fig.4 The SuperDARN radar at Rankin Inlet (RKN) had a strong echo signal over the Hall Beach station between 20∶00 and 22∶00 UT on September 9, 2015 (The red dot is the Hall Beach location; 60°， 70°， 80° represent geographic latitude)

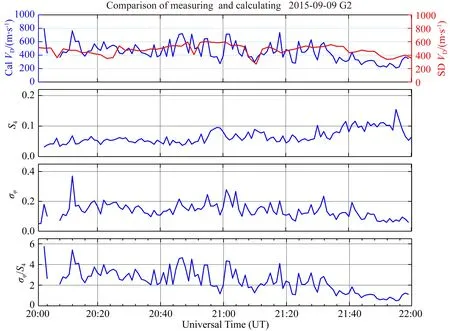
图5 2015年9月9日20∶00—22∶00 UT期间，对流速度的模型计算值(蓝线，Cal VD)与Rankin Inlet SuperDARN雷达的测量值(红线，SD VD)，以及G2卫星与Hall Beach闪烁接收机链路上测量的σφ，S4和σφ/S4Fig.5 During 20∶00 to 22∶00 UT on September 9, 2015, the drift speed calculated by model (blue line, Cal VD) and measured by SuperDARN radar (red line, SD VD) from Rankin Inlet (RKN), and σφ，S4，σφ/S4measured on the link between the G2 satellite and the Hall Beach scintillation receiver

图5中的蓝色线分别展示了这两个小时内G2卫星报告的两个闪烁指数及其比值以及根据这个比值反演计算出的对流速度随时间的变化情况，时间分辨率为1 min；红色线为同一时间内SuperDARN雷达测量的对流速度随时间的变化情况，时间分辨率为2 min.第一个子图显示计算速度围绕在测量速度附近上下波动，故对这两个小时内的速度求平均，得到测量速度与计算速度的平均值分别为478.66 m·s-1和440.1891 m·s-1，它们之间的绝对误差约为-38.47 m·s-1，相对误差约为8.04%.这一较小的误差可以初步说明在一个较长的闪烁期间，用该方法计算出的对流速度平均值可以作为真实对流速度的近似估计.

(25)

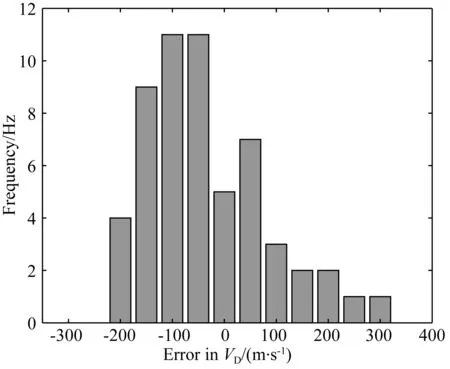
图6 2015年9月9日20∶00—22∶00UT内的对流速度计算值相比于观测值的误差统计Fig.6 Histogram of errors between calculated and measured drift speed from 20∶00 to 22∶00UT on September 9, 2015

(26)

其中

公式(25)是关于z的递增函数，当给定的散射高度低于真实散射高度(zp*)时，对流速度的模型计算值会低于真实值.因此，我们认为图6中对流速度计算值一般小于观测值可能源于给定的散射高度(350 km)低于真实散射高度，或者给定的相位谱指数(p=3)大于真实相位谱指数.

此外，从图6中还可看出公式计算的结果与测量结果的时间对应并不理想，单时刻的速度偏差可以达到两百多米每秒.这一结果也与Carrano等(2016)将该方法应用于低纬地区三个台站得到的误差统计结果相符合.在他们的研究中发现用该方法计算的电离层对流速度估计值相对于其平均值具有大约60%～70%的散布.但考虑到计算该理论所需的众多假设，我们认为这个结果是可以接受的.

为了验证公式(22)中的线性关系，图7展示了对流速度计算值与闪烁指数之比的线性拟合图像，拟合相关系数为0.963，说明该方法计算的电离层对流速度的计算值与闪烁指数的比值之间确实有相当好的线性关系.这一结论也与王勇等(2018)将2013—2015年3年磁正午附近(区域69°～75° MLat和11∶00—13∶00 MLT)GISTM台站观测的闪烁数据与SuperDARN雷达的对流速度观测数据进行线性拟合的结果相符.他们的工作中发现了相位闪烁指数与SuperDARN雷达速度测量值有很好的线性关系，相关系数为0.975，而幅度闪烁指数与测量值的拟合直线的回归系数非常小，可以认为幅度闪烁指数与对流速度线性无关，故相位闪烁指数除以幅度闪烁指数应与对流速度线性相关.这一观测规律可以一定程度上证明本文基于弱散射条件下的电离层闪烁理论所建立的电离层对流速度与闪烁指数的线性关系的正确性.

图7 模型计算电离层对流速度VD(m·s-1)与σφ/S4的线性拟合图像Fig.7 Linear fit image of σφ/S4 and ionospheric drift speed calculated by model

3.2 极区电离层闪烁典型事件分析

为了进一步验证该方法在极区的适用性，本文基于对3.1节的典型闪烁事件的分析，提出以下闪烁事件选取标准并给出选取原因：

(1) 标准1：事件应发生在SYM-H指数小于-50 nT的磁暴事件期间.原因：Aarons(1982)曾分析了1972年8月3—10日强磁扰期间不同纬度上的闪烁情况, 得出磁暴会引起高纬闪烁活动极大增强的结论，所以在磁暴发生期间更易找到强度较高的较为典型的闪烁事件.

(2) 标准2：探测到闪烁的卫星应在Hall Beach台站上方以至少20°的仰角穿越.原因：减少由地面物体的多径反射造成的测量误差.

(3) 标准3：研究时间段内SuperDARN雷达有电离层对流速度的观测值.原因：SuperDARN雷达观测的对流速度既可以作为闪烁发生的粗略判断标准也可作为真实值与模型计算值进行对比.

(4) 标准4：研究时间段中有效数据点的数量应超过总数据点的80%.原因：减少由数据点缺失造成的误差，增加数据的有效性.

由上述闪烁事件选取标准，我们从2015年的11次磁暴发生期间选取出8次闪烁事件进行与3.1节相同的分析.先利用1.3节中由闪烁指数计算对流速度的(22)式计算出各个事件发生期间的电离层对流速度的平均值，再与SuperDARN雷达直接测得的对流速度进行对比分析，最后将计算速度与闪烁指数进行线性拟合，将回归系数以及相关系数等展示在表1中.

由表1可得，第一，计算速度的平均值与观测速度的平均值误差较小，大部分在正负几十最多到百米每秒、二者较为接近；第二，计算速度与σφ/S4的相关系数基本都在0.9以上，说明电离层对流速度的计算值与闪烁指数的比值之间确实有相当好的线性关系.这与前面分析典型事件时得出的结论一致，有力地证明了该方法在极区的适用性.

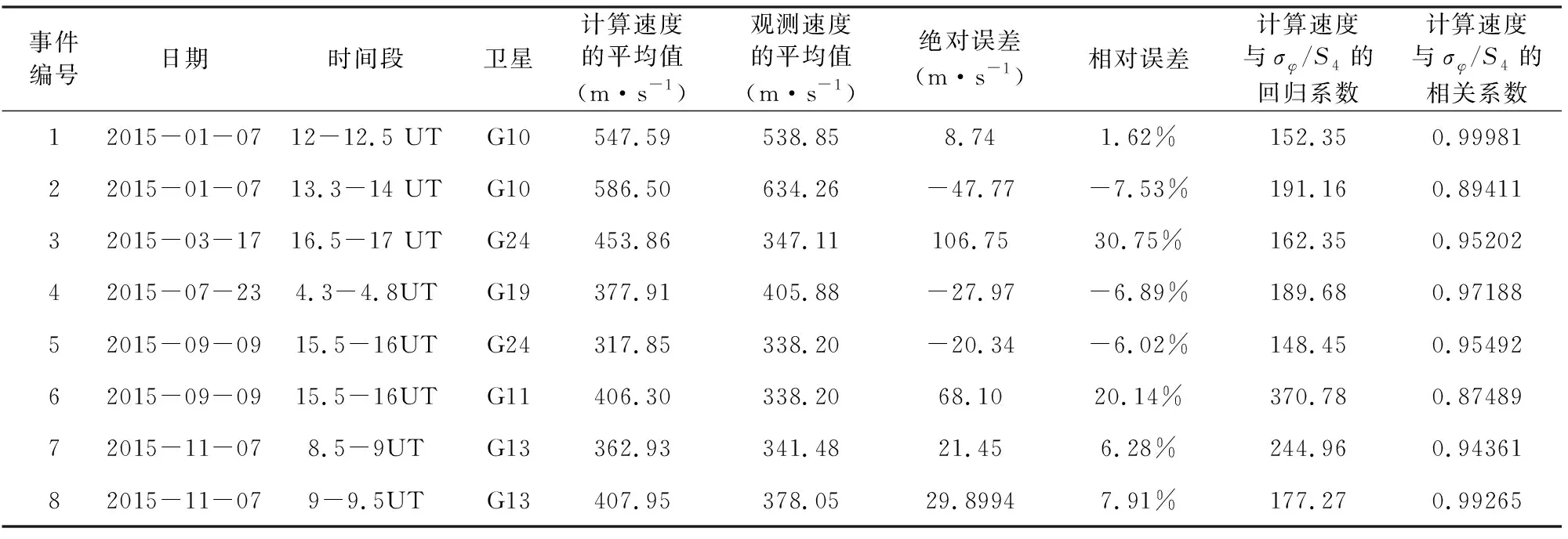
表1 2015年磁暴期间闪烁事件的分析与统计结果Table 1 Analysis and statistical results of scintillation events during magnetic storm in 2015

4 结论

电离层闪烁现象与人们的生活息息相关，尤其是对当今被广泛使用的卫星导航定位、遥感、无线电通信等应用有着不可忽视的影响.而电离层不均匀体作为电离层中的一种常见结构，其运动和演化与电离层对流息息相关，同时也对电离层闪烁的发生有着重要影响.近年来，极区电离层闪烁的研究与建模越来越重视电离层对流速度与闪烁指数之间的关系.本文紧紧围绕极区电离层对流速度与闪烁指数的关系展开研究，取得了如下主要研究结果：

(1) 基于弱散射条件下的电离层闪烁理论，建立并验证了高纬极区电离层闪烁指数与电离层对流速度之间的线性关系，加深了我们对极区电离层闪烁的理论认知.

(2) 利用2015年9月9日20∶00—22∶00 UT的典型闪烁事件期间加拿大Hall Beach的地面接收机及覆盖其上空的SuperDARN雷达等的观测数据，构建了使用极区电离层闪烁指数来反演其对流速度的方法，并初步证明了该方法的计算值可以作为真实电离层对流速度的近似估计.

(3) 通过对典型闪烁事件的分析，提出了一个闪烁事件选取的标准，然后根据这一标准挑选并分析了2015年磁暴期间发生在Hall Beach地区的9个闪烁事件；基于实测数据进一步验证了对流速度与σφ/S4线性关系的正确性以及运用极区电离层闪烁指数来反演对流速度方法的有效性，提供了一种获取极区电离层对流速度/闪烁指数的新途径.

本文的研究还具有良好的发展空间，目前的研究展望如下：

(1) 目前研究的数据量较少，为了更充分地研究极区电离层闪烁特性，有待于对更多站点及更多数据来进一步地验证理论关系以及进行统计分析，并尝试将该模型推广到整个高纬度地区.

(2) 目前基于对流速度只沿地磁纬向的假设，该理论只能计算反演出电离层对流速度大小，有待于对算法进行改进使可以计算出速度的方向，这对研究极区电离层中不均匀体的运动和演化十分重要.

致谢衷心感谢新布伦瑞克大学建设并运行的加拿大高纬度北极电离层监测网(CHAIN)提供的GPS接收机数据(http:∥chain.physics.unb.ca/chain/)；感谢超级双子极光雷达网(SuperDARN)国际组织和弗吉尼亚理工大学提供的雷达数据(http:∥vt.superdarn.org/). 感谢CHAIN首席科学家P. T. Jayachandran教授和山东大学空间科学研究院的Balan Nanan教授有益的讨论.