基于传播矩阵法改进的SS及其前驱波合成算法

王培锋， 周勇， 徐敏

1 中国科学院边缘海与大洋地质重点实验室， 南海海洋研究所， 南海生态环境工程创新研究院， 广州 511458 2 南方海洋科学与工程广东省实验室(广州)， 广州 511458 3 中国科学院大学地球与行星科学学院， 北京 100049 4 南方科技大学海洋科学与工程系， 深圳 518055

0 引言

410 km和660 km间断面作为地幔转换带的上下边界，在地幔动力学研究中有着重要的地位(Helffrich，2000；Shearer，2000；Deuss，2009).针对410 km和660 km间断面的研究有助于了解其形态以及周围物质相互作用情况，可以为地球内部演化提供重要信息(Morgan and Shearer，1993；蒋志勇等，2003；臧绍先等，2003；沈旭章和周蕙兰，2009；王炳瑜等，2013；高占永等，2015；刘震等，2016；李文兰等，2018).矿物学研究表明，410 km和660 km间断面的形成与橄榄石相变有关(Ita and Stixrude，1992).在410 km间断面处，橄榄石转变为瓦兹利石(Wadsleyite)，这种相变具有正的克拉伯龙斜率，表明随着温度升高，需要更高的压力才能发生相变，即相变发生在更深处.而660 km间断面则较为复杂，在通常情况下，林伍德石(Ringwoodite)在660 km间断面处分解为铁方镁石(Ferropericlase)和布里奇曼石(Bridgemanite)，这种相变具有负的克拉伯龙斜率(Bina and Helffrich，1994；Frost，2008).故在温度较高的区域，410 km间断面的位置会比较深，而660 km间断面的位置会比较浅，反之亦然.利用矿物实验测得的克拉伯龙斜率，可将间断面的地形起伏与地幔温度的横向变化联系起来.观测到的阻抗差则可以用于约束橄榄石的含量(Zhang and Bass，2016).此外，镁铁榴石(Majorite)到布里奇曼石的转变也会对660 km间断面的阻抗差观测产生影响(Frost，2008).

地震学为研究410 km和660 km间断面特征提供了许多方法，例如接收函数(receiver function)(王晨阳和黄金莉，2012；白一鸣等，2018；陈一方等，2019；黄河等，2020；何静和吴庆举，2020；Zhang and Schmandt，2019；Pugh et al.，2021；Mark et al.，2021)、三重震相(triplication)(张瑞青等，2011；王秀姣等，2018；Chu et al.，2012；Lai et al.，2019)、源端散射波形(source side scattered waveforms)(Li and Yuen，2014；Zhang et al.，2017)和非对称后向散射波形(asymmetric backscattering waves)(Wu et al.，2019)等.这些方法具有各自的优势，以接收函数为例，该方法可以对台站下方的地幔间断面进行高分辨率成像，在密集台网处可获得较为连续的地幔间断面起伏情况.而SS/PP前驱波方法由于对震源与台站中间反射点下方的地幔间断面敏感，具有较好的全球覆盖性，被广泛应用于地幔间断面的研究中(Deuss，2009；马宇岩和盖增喜，2018；肖勇等，2021)(图1).

图1 SS及其前驱波(S410S和S660S)射线路径示意图浅灰色部分代表海洋，暗灰色部分代表山脉.Fig.1 Schematic diagram of the ray paths of SS and its precursors (S410S and S660S)Oceans and mountains are denoted with the lightgray and dimgray blocks，respectively.

有限差分法(finite-difference method)(Smith，1975；Zhang and Chen，2006)和谱元法(spectral-element method)(Komatitsch and Tromp，2002a，b)是可用于模拟大震中距的SS及其前驱波波形的数值模拟方法.有限差分法几十年来一直是许多研究应用的主力，在地震学研究中得以广泛应用.有限差分法的数学简单性使其可以快速适应特定问题，设计良好的有限差分算法甚至能胜过在数学上更复杂的技术(Igel，2017).例如有限差分法可采用轴对称近似(Igel and Weber，1995，1996；Chaljub and Tarantola，1997)和三维球面截面(Igel et al.，2002)，用球坐标公式求解全球波传播问题.谱元法结合了伪谱法的高精度和有限元的灵活性优点，成为在全球尺度应用越来越广泛的地震波数值模拟方法(Komatitsch et al.，2002).Chaljub等(2003)使用了Ronchi等(1996)发展的立方球体概念，实现了对3D非均匀球体地球中完整波场的模拟.

尽管有限差分法和谱元法可以高精度地模拟全球尺度的地震波传播，但这往往需要大量的计算，难以应用于反射点广泛分布的SS及其前驱波模拟.在一维框架下实现的传播矩阵法由于其计算的高效性和结果的准确性，较早被广泛用于地震波波形模拟.传播矩阵法是由Thomson(1950)和Haskell(1953)引入计算地震学，用于研究弹性波在多层介质中的传播.Thomson-Haskell传播矩阵法形式简单，但在高频的情况下，波传播的模态计算表现出数值不稳定性.对此，Knopoff(1964)和Dunkin(1965)各提出了不同的矩阵形式，通过将传播矩阵分离成不同部分，有效地避免了这个问题.目前，Kennett(2009)给出的递归算法被广泛使用，因为它使用反射-透射系数矩阵，所以递归算法被许多地震学家简称为“反射率法”.

本文基于传播矩阵法改进了SS及其前驱波波形的合成算法，该算法具有快速、准确的特点.通过简单层状模型对该算法及相应程序进行了准确性和计算效率测试.将程序结果与谱元法模拟的波形对比，验证其用于SS 及其前驱波模拟的有效性.在上述工作的基础上，探讨了新算法在研究全球近地表复杂结构对地幔间断面复杂性探测影响中的应用.

1 基本原理

传播矩阵是计算平面波水平分层模型响应的一种有效方法.通过建立不同类型的位移和应力方程组，传播矩阵法被广泛应用于模拟体波和面波的传播(Haskell，1960).

假定一定慢度的平面S波入射水平分层介质(图2)，根据广义传播矩阵，在第i层、深度为z的位移和应力可表达为

fi(z)=EiΛi(z)Ci,

(1)

其中，fi(z)是一个表示随深度变化的质点位移、应力组成的列向量.Ei是由特征向量组成的层矩阵，它取决于介质的弹性性质以及水平慢度和角频率，而Λi(z)是竖向相位因子.Ci是由常数组成的向量，表征下行波和上行波能量的大小.

图2 分层模型和坐标系Sinc和Sref分别表示底部入射波和反射波.入射S波系数设为1，R为S波反射系数.虚线示意固体层S波传播.Fig.2 Layered model configuration and coordinate systemSinc and Sref represent the incident and reflected S wave from the bottom layer respectively. The coefficient of incident S wave is set to 1，while R is the coefficient of the reflected S wave. Dashed lines indicate S wave propagation within the solid layers.

由介质连续性条件，f在第i层和第i+1层连续，可推得

fi=Pi+1fi+1,

(2)

其中

(3)

矩阵Pi+1可以把解从zi传播到zi+1，故被称为传播矩阵.

1.1 常规算法

以SH为例，

(4)

(5)

Λi(z-zref)=

(6)

(7)

根据定义，底层的上行波、下行波系数为

(8)

其中R为广义SS反射系数.结合式(1)和式(8)，可得

(9)

由海底边界条件，当位移和应力分量向上传播到海底时，可以表示为

(10)

其中

M=P1P2…PnEn+1,

(11)

考虑到固液界面的切向牵引力为零，有

Ty=τyy|z=0=0.

(12)

结合式(12)，以矩阵的形式重塑式(4)，可得

(13)

结合式(10)，可将式(13)改写为

(14)

其中N1=M21，N2=M22.Mij表示矩阵M中第i行、第j列的元素.

简化式(14)，可得

(15)

再结合式(8)和式(3)，可以得到广义SS反射系数为

(16)

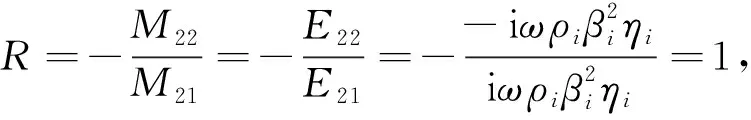
1.2 改进算法

在先前的工作中，我们实现了常规的传播矩阵算法，并且成功计算了PP及其前驱波(Zhou et al.，2020).针对SH系统，本文结合数值计算的特点进行了算法优化，对部分公式进行了改进.重塑式(5)，可得

(17)

其逆矩阵可表示为

(18)

(19)

在新的算法中，我们生成与ω无关的矩阵E′、E′-1以及Λ′-1，将ω相关的计算置于计算M的式(11)中.波形合成步骤与Zhou等(2020)一致.由于计算过程中减少了大量元素与ω的运算，可有效提高算法计算效率.与先前算法(Zhou et al.，2020)相比，改进算法可节约超过一半的计算时间.该改进算法可拓展应用于P-SV系统中地震波的模拟.

2 算法测试

2.1 简单层状模型

基于传播矩阵法，我们利用MATLAB开发了合成SS及其前驱波的程序FASHSHWF.为了测试程序的有效性，我们计算了简单层状模型的合成结果.模型取自PREM(Dziewonski and Anderson，1981)的前三层(表1)，用高斯分布状的子波从底部垂直入射，计算得到其对应的反射波波形(图3).

表1 简单层状模型参数Table 1 Parameters of a simple layered model

图3 入射波形与反射波形实线代表垂直于界面的入射波形.虚线为FASHSHWF合成的反射波形.数字1—5代表震相编号.Fig.3 Incident and reflected waveformsThe solid line indicates the incident waveform perpendicular to the interface，and the dashed line for the reflection waveform simulated by FASHSHWF. The seismic phases are labeled with 1—5.

我们基于FASHSHWF合成的反射波形(图3)测量了各个震相的到时和振幅，并与理论值进行对比.结果显示，程序FASHSHWF拟合的波形到时绝对误差小于0.03 s，而振幅相对误差则小于0.20%(表2)，表明程序计算的准确性.

表2 合成波形到时和振幅的测量值与理论计算值的比较Table 2 Comparison of measured arrival times and amplitudes from synthetic waveform and corresponding theoretical values

2.2 SS及其前驱波合成波形计算

FASHSHWF程序在简单层状模型测试中验证了其波形计算的高精度特征，使得将其用于合成地幔间断面前驱波变为可行.在前驱波的研究中，通常使用MW6.0～7.0的地震事件(Deuss，2009).基于矩震级MW6.5的地震事件估算了其对应的入射波波形，并使用三个不同模型作为输入：(1)PREM；(2)PREM的地幔部分+CRUST1.0(Laske et al.，2013)在青藏高原(86.5°E，27.5°N)处的地壳部分；(3)PREM的地幔部分+CRUST1.0在马里亚纳海沟(142.5°E，11.5°N)处的地壳部分.通过FASHSHWF程序计算合成地震记录，并使用15～75 s的滤波频带(Deuss，2009)进行了处理，所得波形以SS震相对齐(图4).对于该地震记录，以PREM作为参考模型，可观测在(86.5°E，27.5°N)处TSS-SdS的值较大，而在(142.5°E，11.5°N)处较小.这与在青藏高原处地壳较厚，而马里亚纳海沟处地壳较薄相一致.

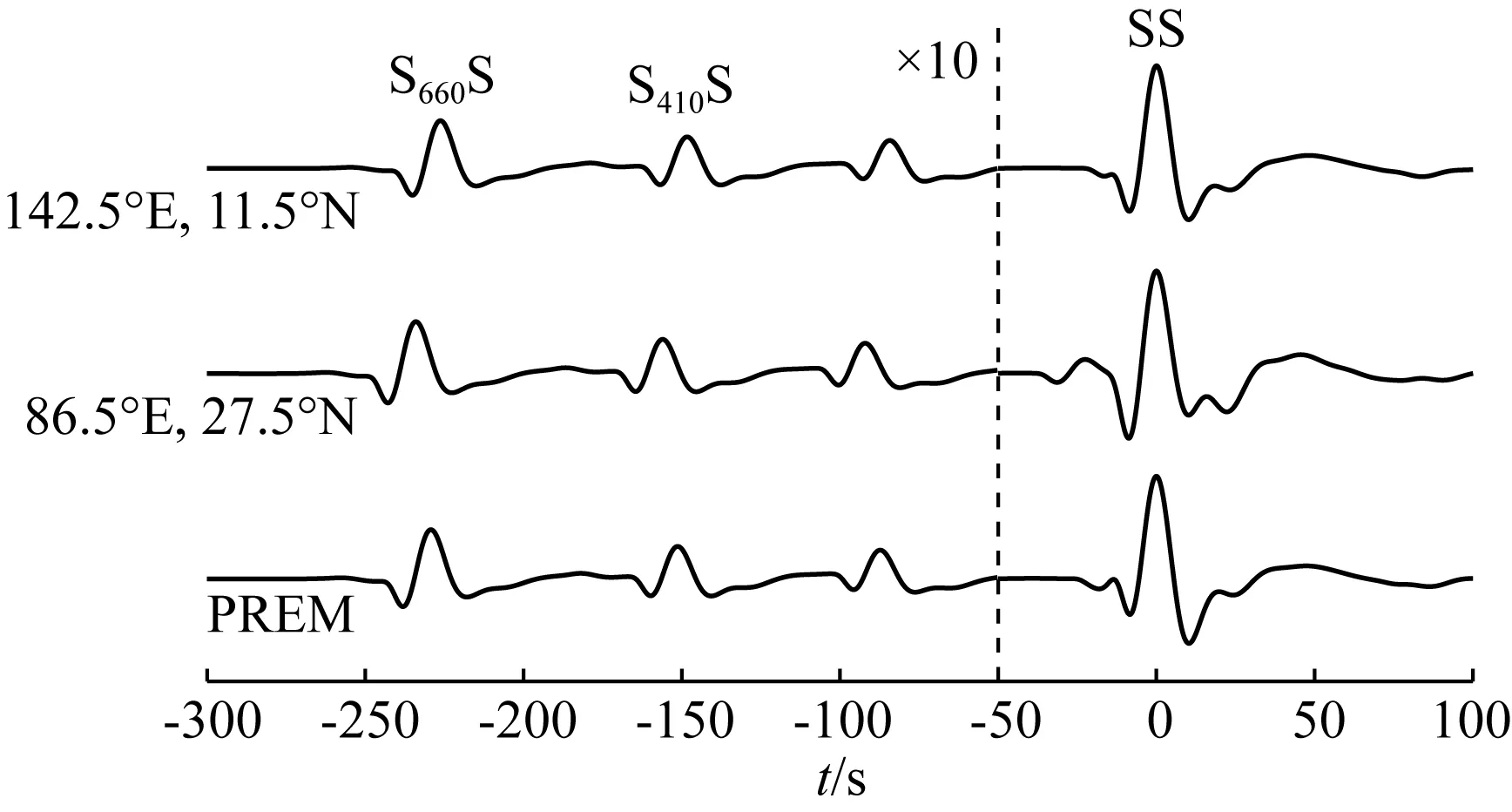
图4 基于FASHSHWF程序合成不同位置的SS及其前驱波波形虚线左侧的波形被放大10倍，便于观察比较.Fig.4 Synthetic SS and its precursors simulated by FASHSHWFThe waveforms to the left of the dashed line are amplified by 10 times for clearer demonstration.

以中国数字地震台网WMQ台站记录的1990年5月13日04∶23∶09.600发生的MW6.4地震(176.064°E，40.296°S)波形为例，对比了观测数据和FASHSHWF合成波形(图5).观测数据自美国地震学研究联合会(Incorporated Research Institutions for Seismology，IRIS)下载后做了去仪器响应、水平分量旋转至T分量和15～75 s带通滤波的处理.在观测的地震波形中可识别SS震相，合成波形中清晰的S660S、S410S则可作为识别观测波形中相应震相的参考.由于观测数据中有噪声存在，单个地震事件波形中一般难以识别出SS前驱波震相.对叠加波形而言，合成波形则极具指示意义.

图5 地震事件波形(实线)与FASHSHWF合成波形(虚线)对比图事件及台站信息见图.波形记录以SS震相对齐.Fig.5 Comparison diagram of seismic event waveform (solid line) and FASHSHWF synthetic waveform (dashed line)See figure for event and station information. Waveforms are aligned with the SS phase.

3 全球SS及其前驱波走时差和振幅比分布

在上述示例中，PREM为一维地球参考模型，通过引入三维地壳模型CRUST1.0合成新的地球模型，可以用FASHSHWF计算由近地表结构主导下SS及其前驱波波形在全球范围的走时差和振幅比分布情况.具体建模过程如下：(1)去除CRUST1.0中地幔部分；(2)根据CRUST1.0下地壳下边界的深度，保留深于该深度的PREM部分；(3)将二者合并为新的模型(图6a与图6b).在步骤2中需要注意的是，CRUST1.0下地壳下边界深度范围在7.4～74.81 km，PREM地壳下边界深度为24.4 km.在CRUST1.0下地壳下边界浅于24.4 km时，保留的PREM部分还含有部分地壳，对于该情况，我们将多余的部分以地幔参数替代(图6a).

图6 使用CRUST1.0与PREM合成地球模型的示意图Fig.6 Schematic diagram of synthetic earth model using CRUST1.0 and PREM

在410 km间断面的全球走时差TSS-S410S分布图中，存在明显的海陆差异，这跟洋壳和陆壳的厚度不同有关(图7a).在海洋中可清楚观察到大洋中脊、海沟等海底地貌引起的走时差别，而陆地上可观测到青藏高原、安第斯山脉等地形单元所引起的走时差别.最小走时差TSS-S410S在海洋里可小于146 s，最大走时差在陆地上则可大于158 s.在410 km间断面的全球振幅比S410S/SS分布图中，海陆差异表现较弱(图7b)，振幅比S410S/SS的值普遍在0.034附近，这与Bai和Ritsema(2013)以及Shearer和Flanagan(1999)等人给出的范围一致.振幅比S410S/SS在北极附近可达最小值，小于0.020，在墨西哥湾处则达到最大值，大于0.038.在加拿大西北部海域、地中海、墨西哥湾等地方存在较为异常的值，这需要将来进一步的探讨.全球走时差TSS-S660S(图7c)和全球振幅比S660S/SS(图7d)特征与410 km间断面的结果相似.

图7 基于CRUST1.0与PREM合成地球模型计算得到的全球走时差TSS-SdS和振幅比SdS/SS分布(a)和(b)分别表示S410S与SS的走时差和振幅比，(c)和(d)分别表示S660S与SS的走时差和振幅比，计算震中距为130°.Fig.7 Global distribution of the differential traveltimes TSS-SdS and the amplitude ratios SdS/SS calculated from synthetic earth model using CRUST1.0 and PREM(a) and (b) represent the differential traveltime and amplitude ratio between S410S and SS，respectively；(c) and (d) represent the differential traveltime and amplitude ratio between S660S and SS，respectively. The epicentral distance for calculation is 130°.

4 讨论

4.1 AxiSEM和FASHSHWF计算结果对比

合成SS及其前驱波的程序FASHSHWF具有快速、准确的特点.我们使用了一种谱元法AxiSEM(Nissen-Meyer et al.，2014)来模拟地震波，并与FASHSHWF算法的波形模拟结果进行比较(图8).

图8 FASHSHWF(红线)和AxiSEM(黑线)计算的合成地震图对比震中距范围为100°～160°，间隔5°.S410S和S660S的到时用斜虚线表示.波形向上到水平虚线被放大10倍，以便观察比较.Fig.8 Comparison of synthetic seismograms computed from FASHSHWF (red line) and AxiSEM(black line)The epicentral distances are from 100° to 160° at an interval of 5°. The arrival times of S410S and S660S are indicated with slant dashed lines. Waveforms up to the horizontal dashed line are amplified by 10 times for clearer demonstration.

我们设置了一个倾滑断层作为AxiSEM的震源机制，提取计算得到的S波波形作为FASHSHWF程序的输入子波，应用希尔伯特变换(Hilbert transform)得到结果.对AxiSEM和FASHSHWF计算的波形都做了同样的带通滤波(15～75 s)后，以SS震相作为参考对齐波形.由FASHSHWF计算得到的SS、S410S和S660S震相与AxiSEM的结果吻合，区别在于AxiSEM的结果中SS前驱波受到两个其他震相(Ss660s和ScS660ScS，Flanagan and Shearer，1998)的干扰(图8).基于传播矩阵的改进算法计算的结果对提取主要震相的参数(如振幅、走时等)具有一定的准确性.通过FASHSHWF模拟的SS前驱波波形近似于数值模拟(例如，AxiSEM)的波形经过曲波变换(Yu et al.，2017)去除干扰震相后的结果.

4.2 改进算法与常规算法计算效率对比

传播矩阵法是在一维框架下实现的方法，具有高计算效率和高精度.即便是比常规的谱元法计算少了一个维度的AxiSEM，在计算效率方面仍弱于传播矩阵法.同时，我们在常规传播矩阵法的基础上改进的算法，进一步提高了计算效率.在保持原有算法的精度下，可节约超过一半的时间，且该优势在层数越多的地球模型中越突出(图9).

图9 本文改进算法(虚线)和常规算法(实线)计算耗时随模型层数的变化Fig.9 Comparison of the computational time between the improved algorithm (dashed line) and the regular algorithm (solid line)

4.3 地幔间断面测量的其他可能影响因素

本文使用FASHSHWF计算得到的波形都是以一维的PREM作为模型输入.而实际上地幔间断面还存在着许多复杂结构，例如410 km间断面的过渡区宽度及其顶部的低速层.高温高压实验表明，地幔转换带具有较高的储水能力.Ohtani(2005)指出，在正常地温梯度下地幔转换带的储水能力为地表水含量的2～3倍.同时，水的加入会使间断面的厚度增加.据估计，410 km间断面的过渡区宽度有4～35 km(Benz and Vidale，1993；Priestley et al.，1994).此外，Bercovici和Karato(2003)根据地幔中水在不同矿物的分配情况，提出了“转换带水过滤器”的假说：在地幔对流过程中，由下地幔的物质经过410 km间断面时，瓦兹利石发生相变形成橄榄石，同时释放出水引起熔融，形成富集不相容元素的熔体.这便是对410 km间断面顶部存在低速层所给出广为接受的解释(Vinnik et al.，2003；Fee and Dueker，2004；Courtier and Revenaugh，2007；Jasbinsek et al.，2010；Schaeffer and Bostock，2010；Vinnik et al.，2010；Hier-Majumder and Tauzin，2017；Zhang et al.，2018).利用FASHSHWF程序，我们探讨了410 km间断面的过渡区宽度及其上方的低速层对SS前驱波波形的影响.

首先研究410 km间断面过渡区宽度对SS前驱波波形的影响.参照Vinnik等(2020)，将PREM中波速和密度的突变以梯度变化替代.其中过渡区宽度设置为20 km (图10a).相比于PREM的结果，增加过渡区宽度后S410S震相的振幅显著降低(图10b)，在经过15～75 s的滤波器滤波后，两者振幅差异减小，但过渡区宽度仍使得S410S震相的振幅降低(图10c).因此若不考虑410 km间断面的过渡区宽度，所得S410S震相的振幅将偏大.

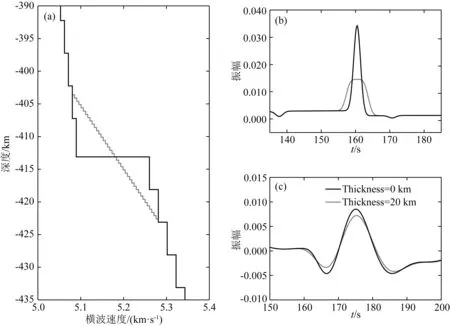
图10 410 km间断面过渡区宽度的影响(a) 添加过渡区宽度的模型； (b) 滤波前的合成S410S震相； (c) 滤波后的合成S410S震相.Fig.10 Effects of the transition zone width of 410 km discontinuity(a) Model with the added width of the transition zone；(b) Synthetic S410S phase before filtering；(c) Synthetic S410S phase after filtering.

在对410 km间断面顶部低速带进行测试时，我们参照Song等(2004)的形式，设置低速带的厚度为10 km，速度为PREM中速度的90%(图11a).相比于PREM，在410 km间断面顶部添加低速带后S410S震相的振幅显著增加(图11b)，在经过15～75 s的滤波器滤波后，两者振幅仍差异较大(图11c).这与该界面阻抗差的增大有关.同时，在S410S震相右侧有一个较强的旁瓣，这与Wei和Shearer(2017)的观测结果一致.因此若不考虑410 km间断面顶部的低速带，所得S410S震相的振幅显著偏小.

图11 410 km间断面顶部低速带的影响(a) 添加低速带的模型； (b) 滤波前的合成S410S震相； (c) 滤波后的合成S410S震相.Fig.11 Effects of the low-velocity layer atop of 410 km discontinuity(a) Model with added low-velocity layer； (b) Synthetic S410S phase before filtering； (c) Synthetic S410S phase after filtering.

上述测试表明410 km间断面的过渡区宽度及其上方的低速层对S410S震相的测定具有影响：过渡区宽度的存在使得S410S震相的振幅降低，而低速层的存在使得S410S震相的振幅增大.由于FASHSHWF仅能处理一维模型，不能考虑地幔间断面起伏带来的影响.为了获得更准确的结果，需要发展可处理地幔间断面起伏(Houser et al.，2008)的SS及其前驱波正演算法.

5 结论

(1)本文基于传播矩阵改进SS及其前驱波波形正演算法FASHSHWF，利用简单层状模型进行测试，结果表明改进算法具有高精度以及高计算效率的特点，较常规算法节约50%以上的时间，适用于地幔间断面前驱波的研究.

(2)结合CRUST1.0地壳模型和PREM构建在全球不同区域变化的一维模型，利用改进算法计算出全球走时差和振幅比分布情况，可为利用SS及其前驱波观测数据约束全球范围内的地幔间断面起伏形态和物理性质提供参考.

(3)利用正演算法FASHSHWF探讨410 km间断面的过渡区宽度及其上方低速层对SS及其前驱波波形的影响，结果表明地幔间断面复杂结构对振幅测量有较大影响，在SS前驱波振幅研究中需考虑该类复杂性.更准确的地幔间断面复杂性影响需发展可考虑起伏界面的SS及其前驱波正演算法.

致谢感谢编辑和评审专家对本文提出的宝贵修改意见.感谢澳大利亚麦考瑞大学袁怀玉博士、浙江大学何小波博士、美国新墨西哥大学张涵博士、中国科学院南海海洋研究所张亚运博士、关慧心博士以及尚正涛同学、陈占营同学对本论文工作提供的帮助.感谢南方科技大学俞春泉博士对算法及程序优化提供的帮助.本文算法使用MATLAB(http:∥mathworks.com)编程实现.地震事件数据下载自IRIS(https:∥www.iris.edu/hq/).图件使用MATLAB和GMT(Wessel et al.，2019)绘制.