煤矿巡检救援机器人行走机构设计

闫小军 ， 王新明

（河北建筑工程学院机械工程学院，河北 张家口 075000）

随着采煤技术的不断发展，在提高采煤效率的同时，采煤安全性也得到很大的改善。但由于我国的矿井环境仍旧十分复杂[1]，不论是日常的安全巡检，还是事故发生后的救援探测，煤矿巡检救援机器人对于保护人员的安全都有着非常重要的意义[2]。而巡检救援机器人移动系统性能的优劣，是其能否成功完成巡检和救援探测任务的关键所在[3]。本文根据煤矿的非机构化地形，结合行走机构越障的基本条件，设计了一种平行四边形履带巡检救援机器人移动系统。

1 巡检救援机器人行走机构整体结构设计

1.1 常见的行走机构方案

机器人行走机构的结构形式主要有轮式、履带式、腿足式以及复合式等，虽然每种形式各有优势，但也各有不足之处。选择和设计移动机构时，除了应首先考虑其使用环境，还应对其工作的稳定性和可靠性等因素进行重点考量[4-5]。

1.1.1 轮式行走机构

轮式行走机构构造简单，在平坦路面环境下行进速度快，有一定的优势，但在非结构化地形中适应能力较低，例如在湿滑松软的路面极易发生打滑的情况。同时，轮式行走机构翻越障碍的高度，受限于驱动轮半径高度[6]，只有在驱动轮中心距离路面的高度大于台阶高度的情况下，才有可能越过该台阶。因此，在一些条件恶劣的环境中，轮式行走机构甚至根本无法胜任前进任务。

1.1.2 履带式行走机构

履带式行走机构与地面接触面积大，越野能力强，即使是泥泞湿滑的路面也不易下陷，但履带轮半径大小会限制其越障的高度，并且当其处于越障临界点时，履带处于单点支撑，稳定性较差，在速度波动和振动等因素的影响下，易出现后翻现象[7]。为了解决该问题，陆续出现了各种摆臂式履带行走机构和履带变形式机构等，但该类行走机构由于底盘相对较低，会出现卡底现象。

1.1.3 腿足式行走机构

腿足式移动机构越障性能优越，其不足之处在于前进速度比较慢，与地面接触面积较小，容易陷入松软的路面，并且该类行走机构结构复杂，成本较高[8]。

1.1.4 其他行走机构

除了上述三种行走机构之外，还有各种各样的复合机构，该类机构地形适应能力强，但也存在运动协调性难度大、生产制造成本高等问题[9-10]。

综合考虑常见的机器人行走机构的特点和性能，结合其使用环境情况，为了使行走机构在综合性能方面能够取得较好的效果，本文设计了一种平行四边形机构四履带移动系统。

1.2 行走机构整体结构设计

该煤矿巡检救援机器人行走机构的具体结构，如图1所示。该行走机构两侧分别是对称的平行四边形机构，并在连杆处布置安装普通履带，本体部分纵向布置两条履带。

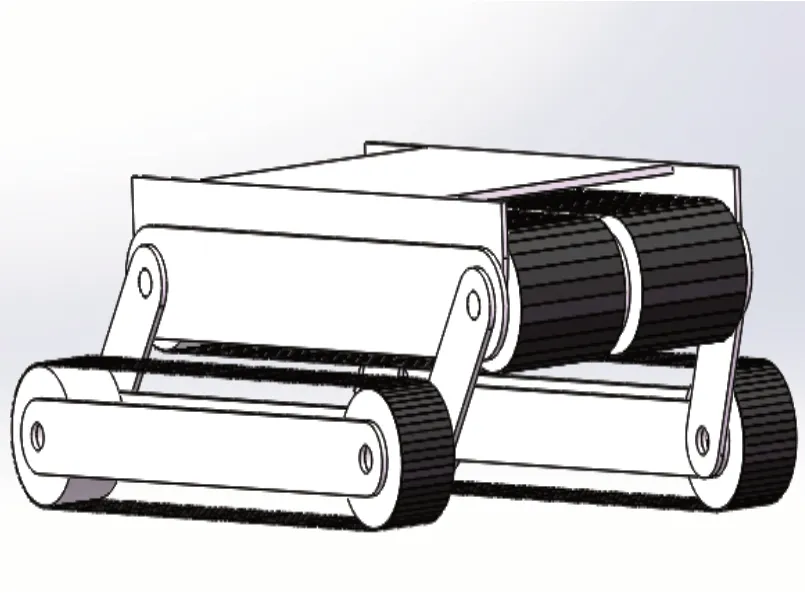
图1 煤矿巡检救援机器人行走机构三维图

当路况较平整时，在平行四边形机构的作用下，两侧履带悬空且与地面不接触，此时机器人依靠本体上纵向布置的两条履带提供前进的动力，如图2所示。

图2 平整路况下行走机构姿态三维图

当遇到湿滑松软的路面以及坡度较陡的路面时，只有巡检救援机器人本体上纵向两条履带工作容易出现下陷、动力不足以及纵向倾覆等问题。此时，平行四边形机构的两短杆转过一定角度并使其和机架处于共线位置，与平行四边形机构相连的侧面两条履带在位于车体偏后方的位置接触地面，并和本体纵向两条履带同时工作，如图3所示。不仅能够有效地抵抗车体的纵向倾覆，增加与地面的接触面积，避免下陷；而且四条履带同时工作，动力也将大大增加。当巡检救援机器人跨越较宽的沟壕时，两侧履带位于机器人本体偏后方的位置并与地面接触，增加机器人整体纵向的长度，有利于跨过较宽的沟壕。

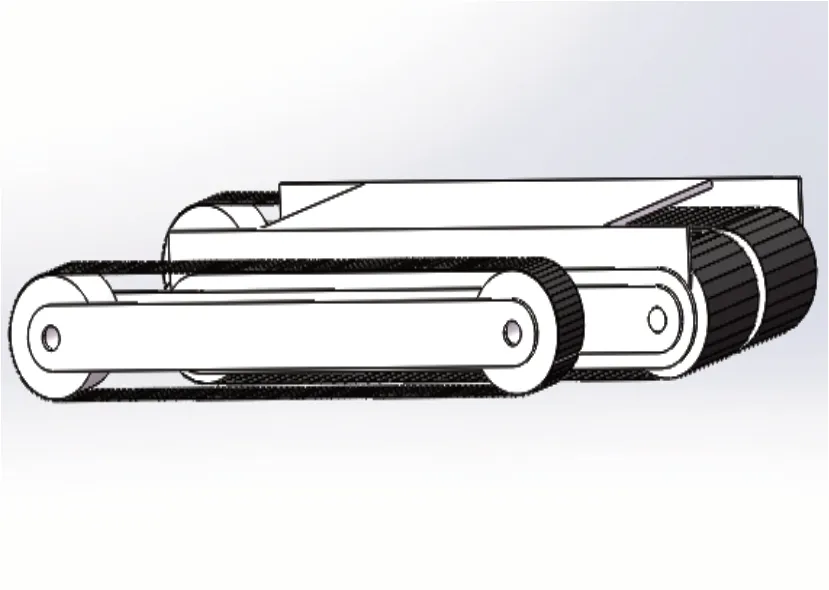
图3 斜坡或松软路面行走机构姿态三维图

当机器人本体有纵向倾覆的趋势时，可通过调整倾覆侧的平行四边形机构，将该侧机器人本体抬高，使两侧平衡，有利于增强车体的横向抗倾覆性，如图4所示。

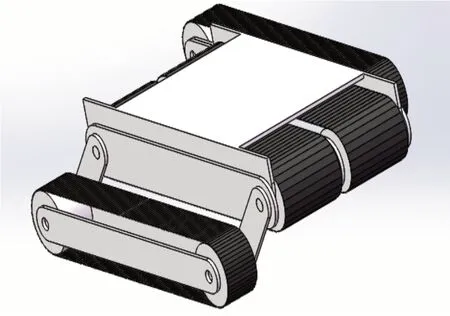
图4 向一侧有颠覆趋势时行走机构姿态三维图

当机器人翻越较高的台阶地形或障碍物时，通过两侧的平行四边形机构变形配合履带的前进来实现。此时，如果车体下方本身发生了卡底现象，由于中间车体有纵向两条履带，可有效避免车体被架空而发生失去动力的情况，如图5所示。

图5 跨越障碍物时姿态三维图

2 行走机构运动特性分析

2.1 平行四边形机构运动的不确定性

当平行四边形机构的两曲柄与机架处于共线位置时，虽然主动曲柄不存在极限位置，机构也不存在死点，但从动曲柄的转向存在不确定性，即可能出现正向或者反向两个方向的转动。若从动杆在此时发生反转，机构出现了不稳定性，这种情况对传动不利。因此，两短杆均设置为同步主动件，从而使从动杆具有确定的运动。

2.2 平坦路况受力分析

在比较平坦的路况下，此时的行走机构只有主履带在工作，如图6所示。

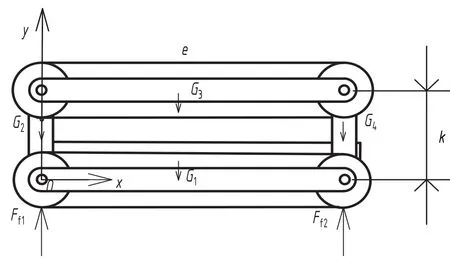
图6 平整路况下受力图

在坐标系xOy中，可得力在y轴投影的平衡方程和对O点力矩平衡方程，如下：

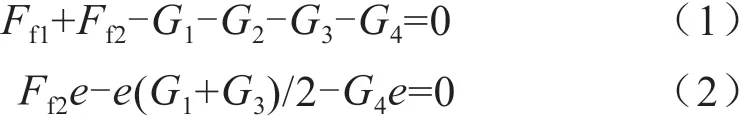
式中，Ff1和Ff2是主履带轮受到地面的临界最大静摩擦力。

2.3 越障临界位置受力分析

机器人翻越台阶初始位置如图7所示，主履带与台阶顶端先接触，当主履带开始搭到台阶上时，平行四边形机构开始顺时针旋转，机器人整体同时进一步向前移动，进入初始阶段。显然，与普通二履带机器人相比，其翻越台阶的能力有了显著的提高，且其最大翻越台阶高度为：

图7 越障初始位置图

式中，b为曲柄长度，R为履带轮半径。

当机器人整体的质心G位于台阶接触点的正上方时，其进入翻越台阶的临界状态，如图8所示。

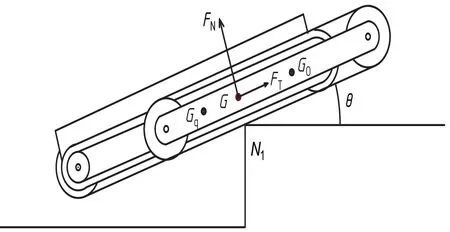
图8 越障临界位置图

与普通二履带行走机构相比，此时其质心位于Gq处，实际上还未到临界状态，由于平行四边形机构质心位于G0点，相当于将机器人整体质心前移，更利于翻越台阶。同时，根据力的平衡原理可知，只要FTcosθ＞FNsinθ，机器人在平衡点会继续保持前进的趋势，从而成功翻越台阶。

3 稳定性分析

为了适应不同路况，随着平行四边形机构曲柄摆动角度的变化，行走机构的位姿各不相同，机器人整体的质心分布也在不断发生变化，偏移中心平面较多时，还会有倾覆的可能性。因此，对质心分布的分析有重要的意义。

如图9所示，先建立直角坐标系xO1y，设该机构的曲柄和连杆长度分别为a和b。连杆上质心位置坐标为G3(l3,h3)，两曲柄质心坐标分别为G2(l2,h2)和G4(l4,h4)，车体质心坐标为G1(l1,h1)。曲柄的摆角为θ，θ∈[0, 2π]。设履带轮的半径（含履带宽度）为R，其整体质心坐标为G(l,h)，则得到质心公式：

图9 任意摆角时机器人各部分质心分布图

式中，l1、l2、h2、h4分别是曲柄摆角θ的函数。

4 结论

本文通过对行走机构特点进行对比分析，结合机器人使用环境设计了一款对称平行四边形机构四履带巡检救援机器人行走机构，并对其翻越台阶临界状态和质心位置进行分析。研究结果表明，与普通二履带机器人行走机构相比，该行走机构具有较强的越障性能和稳定性。