面向板材安装的双臂机器人设计与分析

蒙 磊，李铁军，李勇斌，李赛雷，杨 冬

（河北工业大学 机械工程学院，天津 300130）

0 引言

建筑机器人最早出现于20世纪80年代，由日本清水公司研发的钢梁防火层喷涂SSR系列机器人[1]。近年来，国外为了提高建筑施工中的工作效率，有效降低成本，改善施工条件，研发出面向不同施工工艺的建筑机器人。葡萄牙里斯本大学[2]基于ABB工业机器人研制了一款将不同比例的混凝土和软木混合物作为材料的3D打印机器人。瑞士苏黎世联邦理工学院[3]研发的In-situ Fabricator砌墙机器人系统是一套用于非特定环境下进行砌筑工作的砌墙机器人系统。美国南加州大学Khoshnevis教授[3]提出的轮廓成型工艺（Contour crafting）理念使得将大型建筑结构与其内部构造的建造过程转向自动化成为了可能。未来建筑机器人也将在宇宙探索、月球和火星开发方面发挥不可替代的作用[4]，美国提出的外星球自主建造机器人构想与样机，代表了建筑机器人的最新技术[5]。

我国建筑机器人研究工作逐渐受到重视，目前已列入“十三五”重点研发计划，并于2016年成立了中国自动化协会建筑机器人专委会[6]。以大学及研究所为主的建筑机器人技术研究团队取得了一定的研究成果。河北工业大学[7]建筑机器人团队研发了大型板材安装机器人系列成果，并已开始工程示范应用。同济大学[8]成功研制出了木构加工机器人，可实现较大尺寸与大曲率木构的加工。哈工大[9]研制了一款可遥控的壁面爬行巡检机器人，可用于各类建筑物壁面检查及喷涂工作。中国科学院沈阳自动化研究所[10]研究开发了挖掘机器人以及水下作业机器人等智能装备。山东科技大学等单位[11]研发了一种煤矿井下喷浆机器人。

近年来，随着我国城镇化速度的加快，玻璃幕墙作为大型建筑物的重要外部装饰部分，使用越来越广泛[12]。但此类玻璃幕墙多数为板型（即板材）存在着质量大、尺寸大等问题，且在安装过程中需要大量施工人员通过建设脚手架等设施安装[13]。这种安装方式效率偏低、施工人员劳动强度大，极易发生意外事故。因此研发一款大型板材安装机器人具有重要意义。

1 混联机械臂结构设计

1.1 板材安装机器人施工工艺

机器人在进行安装板材时，为了便于安装，一般是先调整姿态后调整位置[7]。在成功抓取板材后的动作流程如图1所示，机器人抓取板材移动到安装位置，完成粗定位，然后完成板材的姿态调整，最后进行精确的定位安装。因此机器人的设计必须保证具有6个自由度及其以上来实现板材安装的位置以及姿态的调整。

图1 板材位姿调整过程

机器人在确定安装姿态后，还需要调整到精确的安装位置，在调整位置的过程中可能会使姿态发生变化，因此在设计过程中除了满足工作空间以及承载力的要求外，还需要解决在位置调整过程中如何保持末端姿态不变的问题，从而便于板材的安装。

1.2 基于平行四边形结构的机械臂设计

普通的串联机械臂行程大，但存在刚度和载荷不足的情况，并联机构存在行程不足的情况，串并混联机构则兼具这两种结构的共同优势。由两组平行四边形与安装在四边形对角线上的液压缸构成的平行四边形机构具备较大的承载力。四边形机构在平面内运动时可以保证末端机构与板材的姿态始终不发生变化，可以保证在板材精确定位过程中不需要反复调节板材姿态。将若干个平行四边形结构串联起来可以起到放到工作空间的作用，使得机器人具备较大工作空间，从而可以独立完成对板材抓取并移动到安装位置这一工序，更好的节约人力。

整体设计方案如图2所示，该机器人的板材安装机械臂共有7个自由度，安装在车体与第一个平行四边形结构间的旋转关节与三个平行四边形结构组成4个自由度，来实现板材安装的位置调节；安装在第三个四边形结构末端的三轴线相交的旋转关节组成三自由度调姿机构，由摆动液压缸驱动，负责板材姿态的精确调整。该机械臂为七自由度冗余机械臂，在施工环境复杂的施工现场具有更好的避障和灵活操作能力。其中一条可作为辅助机械臂，搭载人工辅助安装。机器人整体由履带车及安装在履带车上的两条机械臂组成。

图2 板材安装机器人图

2 运动学分析

根据上文整体设计方案图2将机械臂简化，如图3所示。为了方便运算，本文采用了几何法[14]与D-H法[15]相结合的方法对该机械臂进行运动分析。先对机械臂的并联结构平行四边形进行分析，然后用几何法对机械臂位置关节进行分析，最后用D-H法对机械臂姿态关节进行分析。

图3 机械臂结构简图

2.1 平行四边结构分析

单个平行四边形机构如图4所示。液压缸安装于平行四边形的对角线位置，左侧MO边与左端机构固定，由液压缸的伸缩带动整个四边形机构在纸面所在平面内转动。

图4 平行四边形结构简图

在图4四边形中，MO边与x轴负方向的夹角固定始终为60°。设第i个四边形结构中液压缸长度、四边形OP边长度、MO长度分别为Li、li、ai。根据三角形公式[7]，从而可得三个四边形结构与x轴正方向的夹角αi为式(1)。根据四边形长度和液压缸伸缩行程，计算得第一和第三个四边形结构相对x轴正向的转动角度范围为-30°到+90°。第二个四边形结构与对x轴正向的转动角度为-90°到+30°。

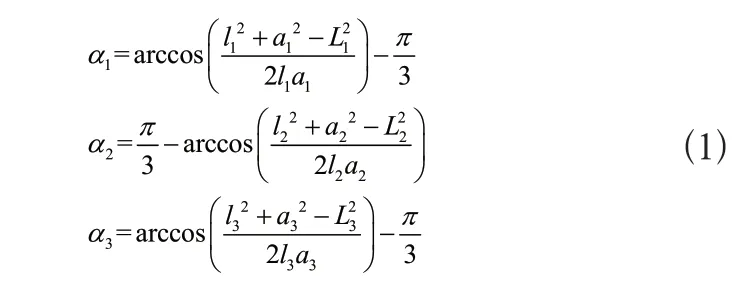
2.2 基于几何法的机械臂位置分析

运用几何方法对机械臂前四个自由度的位置进行分析。如图3中，将基坐标系建于A点，可得B点在xoyfalse平面内的位置为(l1cos α1,l1sin α1)T，C点相对于B点的位置始终不变，同理可得出C、D、E、F的位置最终可得末端点G点在xoy平面内的位置为：

其中αi为第i个平行四边形中液压缸与x轴的夹角，m为FG、BC、DE长度之和，为一固定值。第一个转动关节转动θ1时，末端位置矢量为(px,py,pz)T其中：

2.3 基于D-H 法的机械臂姿态分析

将可以调整姿态的第一个关节角与后三个关节角应用改进的D-H法建立坐标系，如图5所示。

图5 D-H坐标系

相邻连杆的坐标系变换公式为：

设自由度为i的机械臂从基坐标{0}到末端执行器坐标{i}的齐次变换矩阵用T表示，则有：

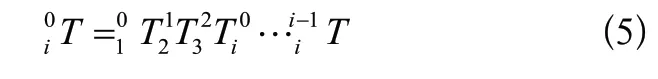
由此建立连杆参数表如表1所示：

表1 机械臂连杆参数

计算各个关节的坐标变换矩阵如下：

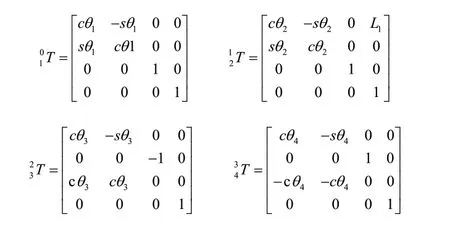
其中θ2θ3θ4代表机械臂第5、6、7三个关节角。

将以上四个矩阵相乘，得：

提取出其中有关姿态的元素，与之前求得的位置矢量重新组合，得到机械臂的位姿矩阵：

2.4 基于改进粒子群算法的机械臂位置逆解

为了方便运算，将机械臂的位置逆解与姿态逆解分开求解。三个串联四边形结构控制末端位置且属于平面冗余机构，冗余机械臂的自运动特性可以改善其运动学与动力学性能，如避障、容错等。

运动学逆解的求解是冗余机械臂研究中的一项重要研究，传统的数值解法速度太慢，难以满足冗余机械臂的实时控制需求。近年来粒子群优化算法、遗传算法、蚁群算法智能优化算法被应用于机器人的逆运动学求解，研究进展其情况较好[17]。基于智能优化算法的机器人运动学逆解求解方法不受机器人构型的限制，具有比较强的通用性，能够克服传统求解方法的不足。

粒子群算法模拟鸟类种群寻找食物，通过搜索、更新当前最优位置与速度来找到全局最优解。该算法具有运算简便、收敛速度快等优点，因此本文采用该算法进行机械臂位置调节部分的逆运动学分析。

2.4.1 适应度函数的建立

在平面内位置正运动学方程有两个等式，三个变量，存在无穷多组运动学逆解。通过附加合适的约束即可以得到最优解。位置正解方程为式(2)所示。建立适应度函数如式(8)所示：

式(8)中αi(k)-αi(k-1)为αi的关节变化量。加权系数t可以减少负载更大的大臂运动量，从而可以节省能源。其中：

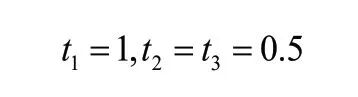
2.4.2 学习因子的改进

标准粒子群优化算法存在易陷入局部最优的问题。本文使用改进学习因子的粒子群算法[18]，可以提高算法的精度的同时使其不易产生取到局部最优值的问题。

本文采用变化的惯性权重系数，在全局搜索时使用较大的系数值而局部搜索时使用较小的系数值，从而提高搜索效率。

学习因子随惯性权重的变化而变化。搜索前期为了提高算法的全域搜索能力，学习因子c1取较大的值且c2取较小的值。反之则可以加强算法的局部搜索能力。学习因子的取值为：

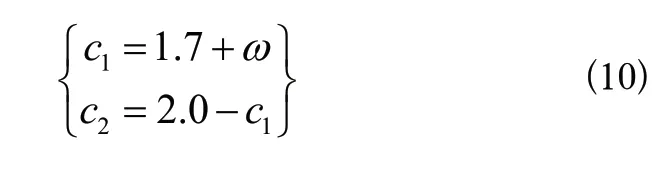
根据改进的粒子群算法并绘制算法流程图如图6所示。

图6 改进的逆解算法流程图

通过给定三维空间内的点，先转化为平面内的点，再通过改进的粒子群算法，可得到一组满足适应度函数的逆解值。

2.5 机械臂姿态逆解

当给定末端姿态时，有如式(11)所示：

将姿态矩阵中的元素与机械臂末端点的位姿矩阵对应相等即可求的关节转动角度。

2.6 机械臂可达工作空间分析

利用运动学位置正解公式，使用MATLAB软件编写逐点搜索法程序得到机械臂平面内与三维空间内的工作空间如图7和图8所示。

图7 机械臂xoy平面内工作空间

图8 三维空间内工作空间

通过工作空间图像可以看出机械臂工作范围较大，可以较好的满足安装板材的工作需求。

3 基于灵活性能的机械臂尺寸优化

3.1 灵活性能指标建立

建筑施工中环境较为复杂，因此机械臂需要在位置调整过程中有较优的灵活性。需要在考虑灵活性能指标的基础上对机械臂的三个平行四边形结构进行尺寸优化。

目前认为雅可比矩阵条件数[19]可以作为重要的灵巧度评价指标，条件数越接近1说明在该位置点的运动性能越优。反之条件数越大说明该位置点越接近奇异。雅可比矩阵条件数λ的表达式为：

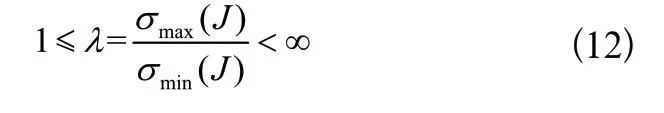
其中σmax(J)和σmin(J)分别表示位置控制部分雅可比矩阵的最大奇异值和最小奇异值。

为了评价结构尺寸参数与灵活性能指标之间的关系，定义机构工作空间内条件数均值为第一个性能评价指标：

同时为了体现条件数的波动情况，定义条件数标准差为第二个全域性能指标：

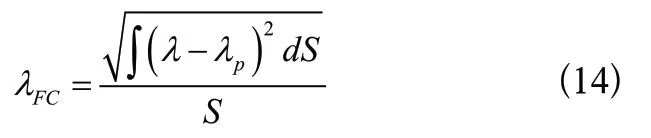
条件数λ越小，代表机构越灵活。因此定义条件数最小值为第三个灵活性指标：

3.2 优化变量设计与分析

将三个平行四边形的连杆长度li作为优化参数。设置优化范围为：

应用单变量法分别绘制l1、l2、l3对三个灵活性能指标的影响。

从图9可以看出λp和λFC随着l1的增加单调增加，λp和λFC性能变差。λDL随着l1的增加单调减小，λDL性能变好。

图9 l1与 λ p、λFCλDL关系

从图10可以看出λp和λDL随着l2的增加单调减小，λp和λDL性能变优。λFC数值基本保持不变。

图10 l2与 λ p、λFCλDL关系

从图11可以看出λp和λFC随着l3的增加单调增加，λp和λFC性能变差。λDL数值基本保持不变。

图11 l3与 λ p、λFCλDL关系

由图10和图11可以确定当l2取1.4和l3取0.8时机构具有最优的灵活性能。对于l1，以上三个灵活性能指标对机械臂灵活性都较为重要，因此将三个灵活性能指标之和CDI作为综合灵巧度评价指标。

绘制l1与CDI关系图如图12所示。

图12 l3与 λ p、λFCλDLfalse关系

由图12可以看出l1在取1.4时机构具有最优的灵活性能。

3.3 优化结果验证

根据雅可比条件数分别绘制优化前与优化后的机械臂工作空间内的条件数等高线。

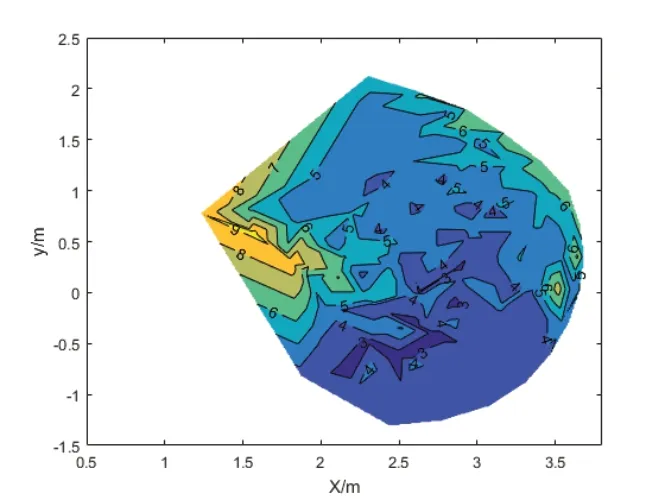
图13 优化前工作空间内条件数等高线图

图14 优化后工作空间内条件数等高线图

计算优化前后的三个灵活性能指标的数值及变化量如表2所示。

表2 优化前后指标值

通过计算优化前后的性能指标值，可以看出三个灵活性能指标值均减小，即位置控制部分灵活性能增加。

4 结语

针对板材安装的工艺流程和对建筑机器人工作空间、承载力的要求，设计了一款基于平行四边形机构的冗余串并混联的板材安装机器人。基于几何法和D-H法，并结合其结构特点建立了机械臂的运动学模型，对其进行了运动学的分析。基于灵巧度对机械臂进行了尺寸优化，提高了机械臂的灵活性能。基于逐点搜索法，通过位置正解公式绘制机械臂工作空间云图。为后续的详细设计与运动控制奠定了理论基础。