基于异形板材自动排料方法研究

柯于河

（中国直升机设计研究所，江西景德镇 333001）

0. 引言

在板材自动排料问题研究中，研究对象只要零件和板材。在最开始研究中，零件都是先拟合成规则图形如三角形、矩形、圆形等，然后在进行排料[2]，之后的研究就直接为二维不规则零件在矩形板材中自动排样。本文在此基础上，研究二维不规则零件在异形板材（非标准矩形板材）自动排样问题。其问题简单描述为：将一定数量的不规则多边形零件，尽可能多排放在一个形状不规则的板材内，并要在排放过程中，多边形零件不能出板材边界间，多边形零件之间不能重叠。

二维不规则零件在异形板材自动排样问题数学表述：

式（1）中C为排放零件，P为异形板材，Ps为排放零件占用异形板材的相对面积。目标函数Zmaх为异形板材相对利用率，其值越大，表示排放结果越好。

二维不规则零件在异形板材自动排样问题中，如果单纯从二维不规则零件角度来看，则只需要考虑2个问题：首先是每次“选择哪个零件”来排放，即零件定序问题，其次是将选择好后的“零件排放在哪里”，即零件定位为题[3]。目前定序问题主要通过智能算法如遗传算法，蚁群算法，模拟退火算法等来解决[4]，这些智能算法都具有较好的全局搜索能力。本文则直接采用应用最为广泛和成熟的遗传算法。零件定位问题是异形板材自动排料中最重要的问题，也是本文研究的重点，本文通过内外临界多边形来确定每个零件可排放位置。

1. 基于临界多边形的零件定位方法

零件在板材排放约束只有2个：零件间不重叠，零件不能出板材边界。这2个约束是很弱的，满足这2个约束的零件可排放点可能为一片区域内的点，对于计算机来说，零件可排放点只能为离散有限解集。临界多边形（nofit-polygon，NFP）是一种可以快速判断多边形是否重叠，是否紧靠的重要几何计算工具，因此在二维不规则排样问题中广泛应用。

临界多边形的定义如下[5]：给定2个多边形，固定其中一个多边形A，另一个多边形B绕多边形A运动一周回到初始位置，在运动过程中多边形B和A至少有一点相接触但不能相交。而且多边形B在运动过程中自身不能有任何旋转，选择多边形B其中一个顶点作为参考点，该参考点随多边形B运动一周所形成的轨迹，称为为多边形B相对于多边形A的临界多边形（为便于表述，在本文中也被称为外临界多边形），记为NFPAB。在异形板材自动排料问题中，临界多边形的最大的意义是当多边形B在临界多边形NFPAB边上时，多边形B和多边形A紧靠，在临界多边形NFPAB内部时，多边形B和多边形A重叠相交，在临界多边形NFPAB外部时，多边形B和多边形A相离。因此可以通过临界多边形很快判断两多边形间的重叠情况，减少了大量图形相交计算。

在矩形板材中，可通过排放零件的各个顶点横纵坐标是否大于矩形板材长宽来快递判断零件是否排出板材边界。而在异型板材中，由于其轮廓相比于矩阵板材是不规则的，为此引用内临界多边形（Inner-no-fit-polygon，INFP）的概念。内临界多边形的定义：给定多边形C和多边形板材D，固定多边形板材D，多边形C绕多边形板材D运动一周回到初始位置，在运动过程中多边形C要和多边形板材D至少有一点相接触但不能相交，而且多边形C在运动过程中自身不能有任何旋转，选择多边形C其中一个顶点作为参考点，该参考点随多边形C运动一周所形成的轨迹，定义为多边形C相对于多边形板材D的内临界多边形，记为INFPC，如图1所示。内临界多边形的最大的意义就是当多边形C在内临界多边形边上或者内部时候，可以保证多边形C不出板材边界。

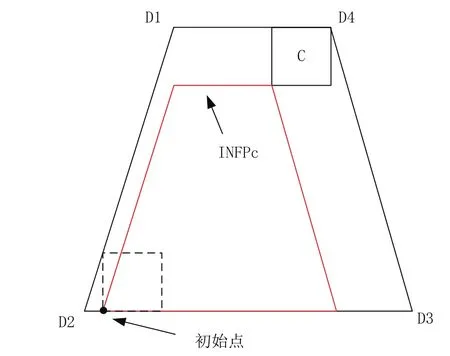
图1 内临界多边形示意图

当零件在临界多边形边上或者顶点处，零件间则恰好紧靠不重叠，当零件在内临界多边形边上或者内部，则可保证零件不出板材，为简化计算量，本文只将临界多边形顶点和其相交的点作为零件排放位置，临界多边形各条边不考虑。下面通过示例来描述在如何通过内外临界多边形来确定零件C可排放位置，其中零件为A，B，C，板材为D，3个零件排放顺序为A-B-C，具体步骤如下：

Step1：排放零件A，初始零件排放位置一般默认为左下角；

Step2：基于零件A和零件B临界多边形，以及零件B于板材D内临界多边形来确定零件B排放位置，此处直接将零件B排放在与零件A和板材D都紧靠位置上，零件A和零件B排放位置如图3（a）虚线所示；

Step3：求出零件C和零件A临界多边形NFPAC，如图2（a）所示，零件C和零件B临界多边形NFPBC，如图2（b）所示，零件C和板材D的内临界多边形INFPC，零件C拟排放点为这3个临界多边形所有顶点以及这3个临界多边形相交的交点，如图3（a）所示；

图2 求解零件间临界多边形

Step4：最终零件C可排放点必须同时满足：临界多边形NFPAC边上或者外部；临界多边形NFPBC边上或者外部；内临界多边形INFPC边上或者内部。不满足其中任何一条的点都应该剔除，最终零件C可排放点，如图3（b）所示；

图3 零件可排放点

Step5：零件C放置在每一个可排放点时候，都可以保证它与零件A和零件B紧靠不重叠且在板材内部，在这些可排放点中选取合适点排放零件C后，后续零件以此类推排放。

2. 基于异形板材有缺陷区域处理办法

在现实中，异形板材内部可能存在已被切割后的区域，这些已被切割后的有缺陷区域无法作为异形板材可排放区域。在实际中对于这类问题中，可以把这些缺陷区域看作一个已排放的“特殊零件”，只要保证后续零件排放不与这些缺陷区域重叠就行，因此只需要在零件定位算法上进行修改，具体步骤如下：

Step1：求解所有零件之间临界多边形、所有零件与每个缺陷区域之间临界多边形、所有零件与板材之间内临界多边形；

Step2：排放初始零件1；

Step3：求出零件2和零件外1临界多边形、求出零件2和每个缺陷外临界多边形，零件2和板材内临界多边形，零件2拟排放点为这些临界多边形所有顶点以及相交的交点；

Step4：剔除掉在任意外临界多边形内部的点或是在任意内临界多边形外部的点，即板材外部点和缺陷区域内部的点以及零件间会重叠的点，剩下点为零件2可排放点；

Step5：确定零件2排放点后，后续零件以此类推排放。

本文从欧洲排样问题兴趣小组ESICUP提供的Shirts的99个零件作为测试零件，然后再设计一个带2缺陷区域的异形板材，最终测试结果如图4所示，从排样结果图可以看出所有零件间没有出现重叠情况，也没有出现板材外部和缺陷区域内部等情况，证明了算法可行性。

图4 带缺陷区域异形板材排样

3.针对异形板材有狭窄区域处理办法

在对随机异形板材测试过程中，一些有狭窄区域的异形板材的板材利用会大大降低，如图5所示，右侧大面积可排区域没有排。通过断点代码运行分析可知，造成这样排样结果是由于每个零件与板材之间的内临界多边形计算错误导致的，从内临界多边形广义范畴来讲，对于这种有狭窄区域特殊的异形板材来讲，每个零件与它之间的内临界多边形应该有2个（左右各一个），零件在这2个内临界多边形任何一个的边上或者内部都可保证零件在其异形板材内部。但在实际计算中，由于初始点从左下角开始的，只计算出左边一个内临界多边形，故零件在排样过程中都只在左边区域排放。

图5 有狭窄区域异形板材排样

针对这种问题，目前无法通过对内临界多边形求解算法改进来完美解决。可以通过排放前的预处理，或是设定阈值来解决。比如当已排零件面积与板材总面积比值小于阈值，或者已排零件区域最大长度、宽度与板材总长度、宽度比值小于阈值时候，可以在剩余板材区域内寻找新的初始排放点继续排放剩余零件，最后将多次排放结果合并。

4.结语

由于目前关于异形板材自动排样研究方面较少，研究该类问题较为权威的欧洲排样问题兴趣小组ESICU也没有相关评估标准和测试实例。因此本文也仅仅从异形板材的自动排样可行性角度上进行研究，从排样结果看，整个排样算法仍然有很大的优化空间。