非线性弹性单盘转子系统稳定性分析

刘继华，苟学中，郑龙席，高仁衡

(1.中国航发四川燃气涡轮研究院，成都 610500；2.西北工业大学动力与能源学院，西安 710072)

1 引言

高转速轻质结构是近代高速旋转机械的设计趋势，它提高了旋转机械的性能，但也引发了很多严重的问题。尤其是线性理论得出的结果不仅误差大，而且无法对实际出现过的自激振动、分岔现象、跳跃现象等做出解释。动力机械工程中，具有强烈非线性的重要组成部分是油膜轴承的转子系统，轴颈转动产生的油膜压力是非线性的。Shaw、Cveticanin对具有非线性弹性轴支撑的转子系统进行了理论和试验分析，表明此类系统存在混沌运动和振动突变现象。

稳定性是指系统受到微小扰动后保持原状态的属性，对于实际工况中的系统，其性能好坏都以系统稳定为前提。转子-轴承系统的运动稳定性问题一直是转子动力学研究的重要课题之一，国内外许多学者都在进行这方面的研究工作。刘继华等基于有限差分法，对轴承-转子系统进行稳定性分析，得出了临界失稳转速，结果表明适当增大偏心率能增加系统的稳定性。薛禹胜在电力系统稳定性分析中提出的互补群群际能量壁垒准则量化理论，在国内外若干电力系统中得到了成功的应用。Xue、李银山等将应用于电力系统的运动稳定性量化理论的研究引入到非线性转子系统。刘继华等采用基于轨迹的加速度-位移扩展平面稳定裕度分析法，得出系统随偏心量参数变化的稳定裕度变化情况。

判别转子系统稳定性的方法较多，Poincare 映射图是判断稳定性的基础。轴颈转动产生的油膜力具有强烈的非线性，是影响系统稳定性的重要原因，这就需要对轴承间隙、润滑油黏度等影响油膜压力的因素进行分析。本文基于Capone 短轴承非线性油膜力模型，对转子系统进行数值计算，采用Poincare映射方法得到转子系统在偏心量、轴承间隙、润滑油黏度3 个参数的特征图，得出失稳转速随上述参数的变化规律。

2 数学模型

以图1 所示的单盘对称转子为研究对象。图中，两端支撑为滑动短轴承，为轴瓦几何中心，为轴颈中心，为转子质心。采用目前广泛应用的简单离散转子模型，将图1中的转子模型离散为3个质点，将轴段处的质量分别离散到轴颈和轮盘处，轴颈只考虑1/8 轴长的质量，轴只有、方向的平动和转动共4 个自由度，约束轴向的平动和转动自由度。单盘转子系统的离散模型如图2 所示，两轴段等效为刚度，轮盘处的阻尼为，非线性油膜力分别作用在两个轴颈处的质点上。

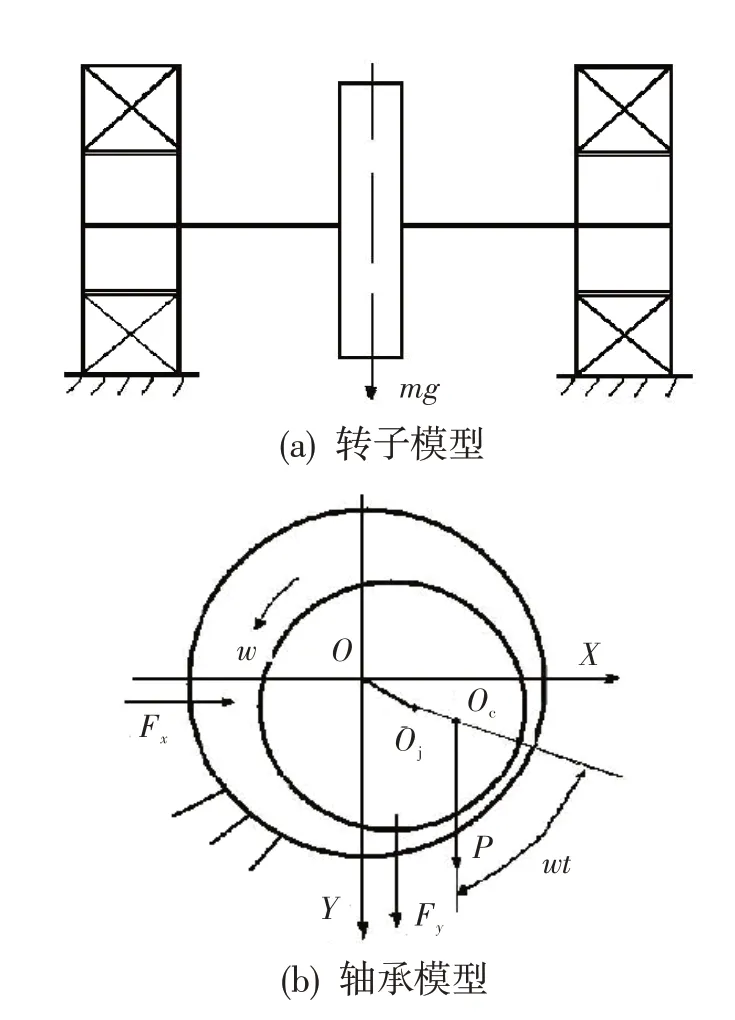
图1 单盘对称转子动力学模型Fig.1 Single disk symmetric rotor model

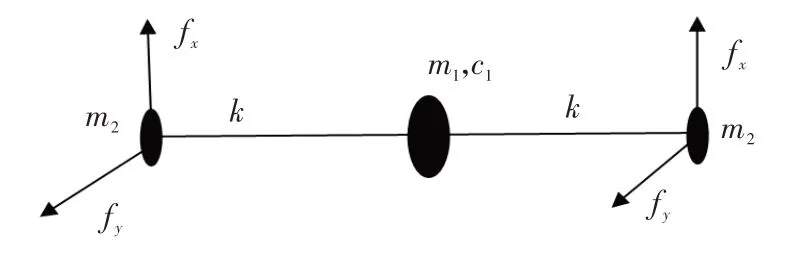
图2 单盘转子系统的离散模型Fig.2 Discrete model of a single disk rotor system

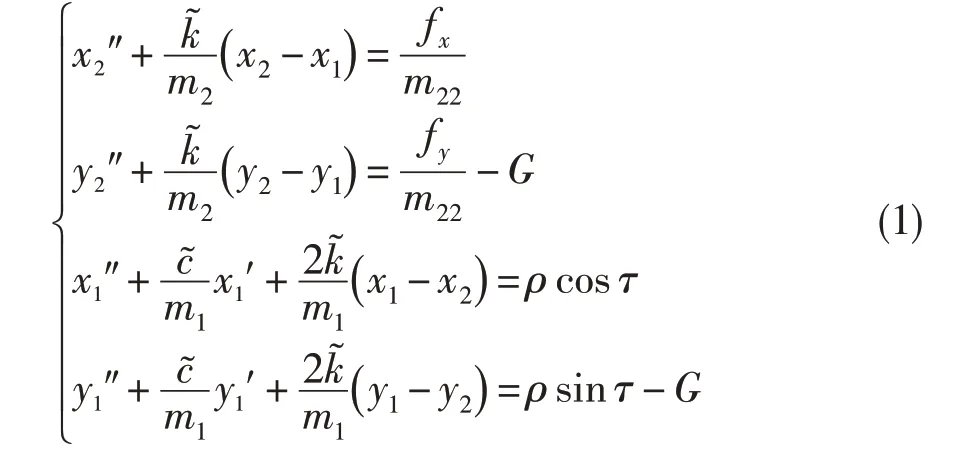
式中：f、f采用Capone 短轴承非线性油膜力模型，其详细表达式见文献[14]；=/()为转子的无量纲重力；=/为无量纲质量，m为单盘处集中质量。

3 数值计算分析

式(1)描述了一个非线性动力学系统的微分耦合方程，可以由数值计算得出近似解。本文使用MATLAB 编程，由于油膜力和基座支撑力的强非线性作用，采用Rung-Kutta法求解。选用的时间步长为2π/100，误差小于10，计算1 500 周期；为消除初值对瞬态响应的影响，去除系统前1 000周期响应数据。在进行系统稳定性分析时，转子模型参数选取为：=420 kg，=50 kg，=28.5 mm，=0.2 mm，=57 mm，=0.018 Pa·s，=2.105×10，=3 000 N·s/m。

3.1 偏心量对转子系统稳定性的影响

为研究转轴和叶轮加工及安装过程中的残余偏心量对转子系统稳定性的影响，首先需在固定偏心量(=0.20)下分析不同转速(=300，430，500，650 rad/s)时的动态响应；然后得出固定偏心量(=0.20)的全局(=300～800 rad/s)分岔图，寻找其分岔点；最后得出偏心量(=0.10～0.40)-转速参数域分岔集。

由于系统在低转速时均表现为工频周期运动，本文只考虑转速在300 rad/s及以上的运动。图3为系统=0.20、=300 rad/s时的动态响应图，可见系统表现为周期运动。图4 为系统=0.20、=430 rad/s时的动态响应图。可以看出，轴心轨迹为几个相交的曲线，在Poincare 图上表现为4 个离散的点；在频谱图上除工频外，还出现了1/4、1/2、3/4 倍频率，由此可以得出系统表现为4倍周期运动。这说明油膜失稳后，除了出现常见的半速涡动，还有涡动频率为1/(=4，6，8…)的高阶次谐波分量。图5 为系统=0.20、=500 rad/s时的动态响应图。可以看出，轴心轨迹为不相交的内凹封闭曲线，在Poincare 图上表现为2 个离散的点；在频谱图上出现了1 个基频和1个半频，且半频幅值比基频幅值大；在时间历程图上表现为较规则的周期运动，出现了2个波峰，说明系统表现为倍周期运动。图6 为系统=0.20、=650 rad/s 时的动态响应图。可见，轴心轨迹表现为几个相交的环形曲线，在Poincare 图上表现为一些离散的点，但这些点并没有形成一定的环形状；在频谱图上出现了几个可以约分的频率，说明系统此时不是概周期运动，而是多倍周期运动。

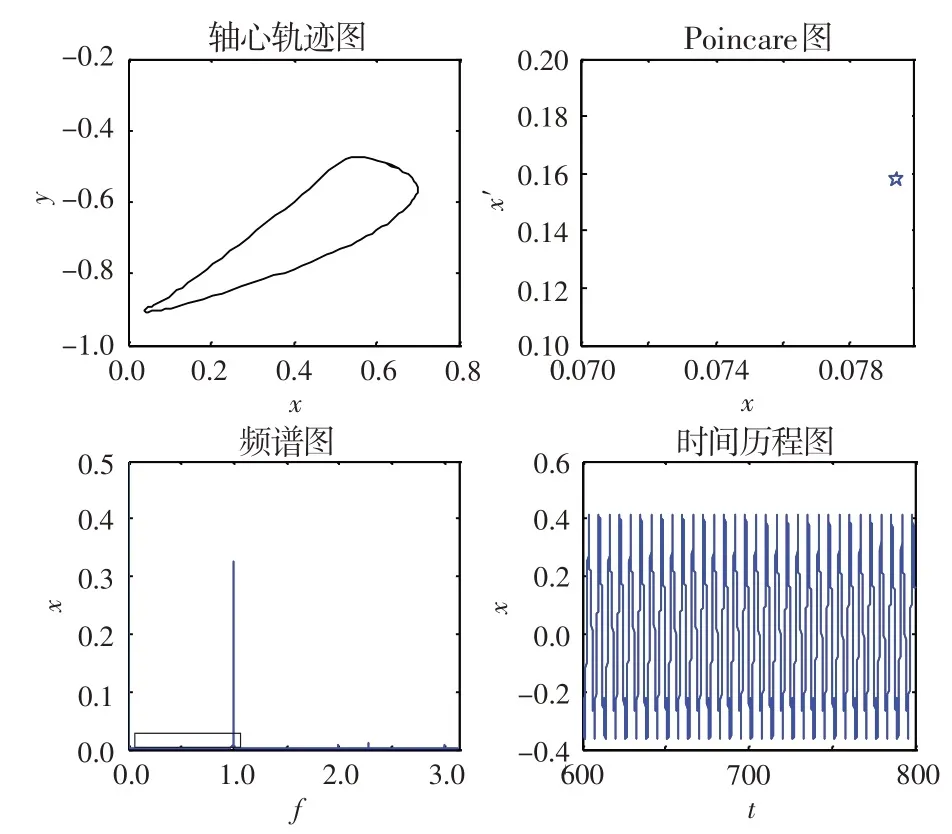
图3 无量纲偏心量为0.20且转速为300 rad/s时的动态响应图Fig.3 Dynamic response diagram(ρ=0.20,w=300 rad/s)

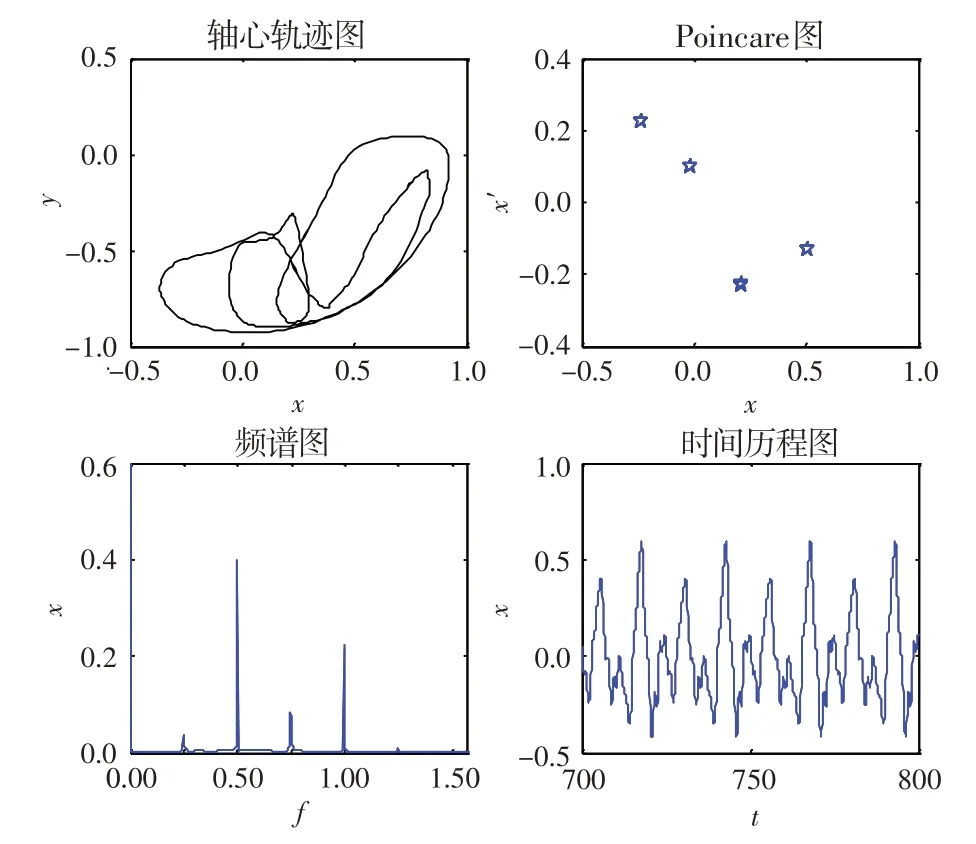
图4 无量纲偏心量为0.20且转速为430 rad/s时的动态响应图Fig.4 Dynamic response diagram(ρ=0.20,w=430 rad/s)

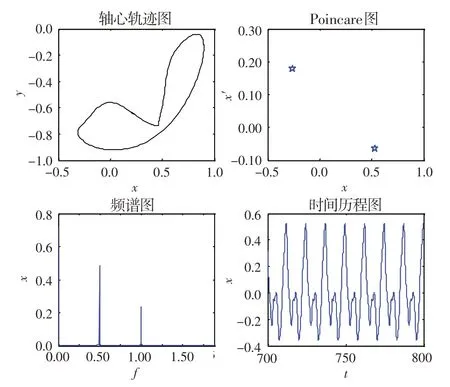
图5 无量纲偏心量为0.20且转速为500 rad/s时的动态响应图Fig.5 Dynamic response diagram(ρ=0.20,w=500 rad/s)

图6 无量纲偏心量为0.20且转速为650 rad/s时的动态响应图Fig.6 Dynamic response diagram(ρ=0.20,w=650 rad/s)

采用Poincare映射方法得出系统=0.20时的全局分岔图，如图7所示。可看出，转速小于等于380 rad/s时，系统都表现为周期运动；转速大于380 rad/s 时，系统的同频周期运动发生分岔而失稳，系统表现为倍周期运动或多倍周期运动。

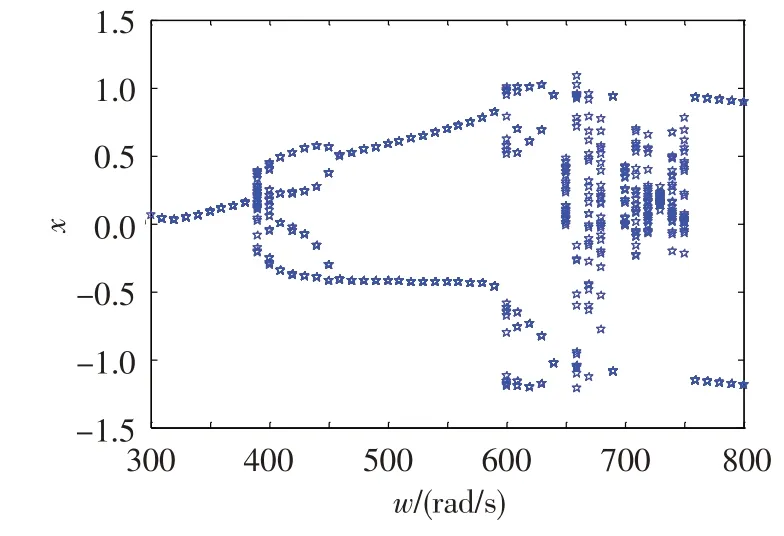
图7 无量纲偏心量为0.20时的全局分岔图Fig.7 Global bifurcation diagram(ρ=0.20)

由于转子系统在不同偏心量时将出现不同的失稳特性，因此有必要研究偏心量对系统稳定性的影响。图8 为转子轴承系统在偏心量-转速参数域内的分岔集。可以看出，无量纲偏心量小于0.25时，随着偏心量增大，失稳转速不断降低，无量纲偏心量大于0.25时，随着偏心量增大，失稳转速又逐渐升高，系统存在着最低分岔失稳转速。此转速不仅和无量纲偏心量有关，而且还和其他因素有关系，系统运行时要特别注意避开。偏心量较小或较大都会增大系统的稳定性，但较大的不平衡力会引起转子轴承受力增大，出现多倍周期运动以及有可能出现跳跃现象。所以为了系统安全运行，必须要对转子进行较高精度的动平衡。本系统平衡后的无量纲偏心量至少要小于0.25。

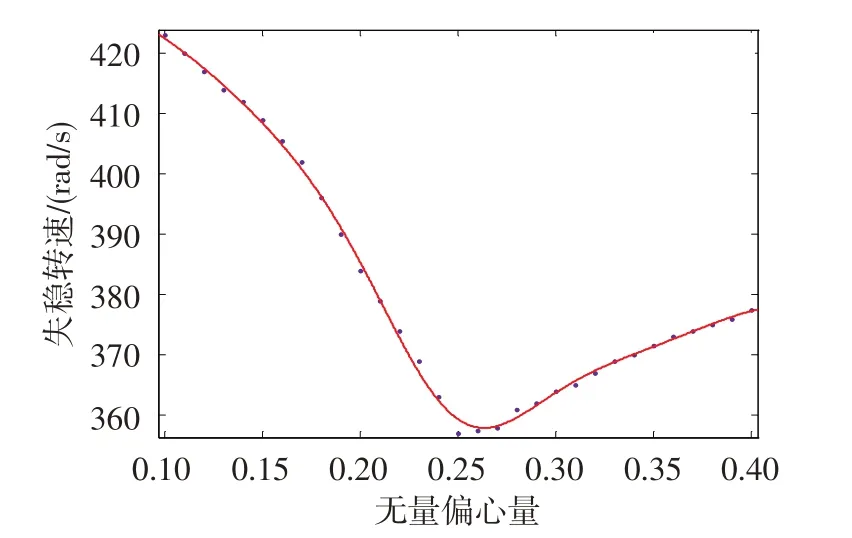
图8 转子轴承系统在偏心量-转速参数域内的分岔集Fig.8 Bifurcation set of rotor bearing system with the parameter domain of eccentricity and speed

3.2 润滑油动力黏度对转子系统稳定性的影响

按照3.1节分析方法，对转子系统无量纲偏心量分别为0.10、0.20、0.30、0.40时的不同润滑动力黏度对系统稳定性的影响进行研究。图9示出了转子轴承系统油膜黏度-转速参数域分岔集。可见，油膜黏度在0.015～0.050 Pa·s 区间，失稳转速都是随着油膜黏度的增加而增加。因此，为了提高系统稳定性和安全性，滑动轴承-转子系统运行时，应选择黏度较大的润滑油。图10 为国内航空发动机常用的某润滑油的黏度-温度曲线。可看出，随着温度降低，润滑油黏度增大。为提高失稳转速，需要对润滑油进行冷却，降低其温度；但润滑油黏度增大又会增加发动机阻力，导致发动机加速时间增大。因此，润滑油黏度需要综合考虑失稳转速和发动机加速性。

图9 转子系统油膜黏度-转速参数域分岔集Fig.9 Bifurcation set of oil film viscosity-speed parameter domain of rotor system

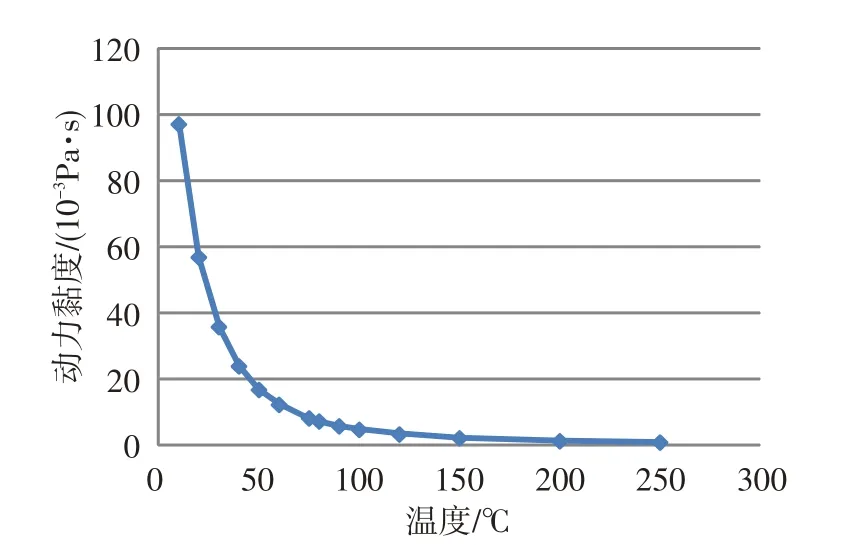
图10 某润滑油的动力黏度-温度曲线Fig.10 Dynamic viscosity and temperature curve of a lubricating oil

表1给出了采用一次函数直线拟合得出的分岔失稳转速与润滑油黏度的关系。可以看出，随着无量纲偏心量的增加，分岔失稳转速随润滑油黏度的增加趋势是先逐渐增大后逐渐减小。从图9可以看出，虽然无量纲偏心量为0.10 时随润滑油黏度的增长趋势较小，但分岔失稳转速始终大于其他无量纲偏心量的。这再次说明，系统运行时，为了增加稳定性，应该对其进行较高精度的动平衡。比较无量纲偏心量为0.30 和0.40 时的分岔失稳转速，黏度较小时无量纲偏心量0.30时的分岔失稳转速大于无量纲偏心量0.40 的，但随着黏度的增大，无量纲偏心量0.30 的分岔失稳转速，逐渐小于无量纲偏心量0.40的。这说明系统的最低失稳转速随黏度变化。

表1 分岔失稳转速与润滑油黏度的关系Table1 The variation trend of bifurcation instability speed with the viscosity of lubricating oil

3.3 轴承间隙对转子系统稳定性的影响

轴承结构直接影响着轴承-转子系统的动态响应，轴承间隙是其中一个重要的参数。为研究轴承间隙对转子系统稳定性的影响，首先需在固定偏心量(=0.02 mm)和轴承间隙(=0.25 mm)下，分析不同转速的动态响应；然后得出固定轴承间隙(=0.25 mm)的全局(=300～800 rad/s)分岔图，寻找其分岔点；最后得出轴承间隙(=0.20～0.30 mm)-转速参数域分岔集。

图11为=660 rad/s时的系统响应图。可见，轴心轨迹为3个圆环，在Poincare图上出现了3个离散点；在频谱图上除工频外，还出现了1/3、2/3倍频，说明此时为3倍周期运动。显然，周期3不可能来自倍周期分岔，混沌学指出，周期3 意味着混沌，这种混沌叫做间隙混沌(阵发混沌)。

图11 轴承间隙为0.25 mm且转速为660 rad/s时的动态响应图Fig.11 Dynamic response diagram(c=0.25 mm,w=660 rad/s)

采用Poincare映射方法得出系统在轴承间隙为0.25 mm 时的全局分岔图，见图12。根据图12 以及上述分析可以得出，在转速低于380 rad/s时，系统表现为工频周期运动；转速超过380 rad/s时，系统的同频周期运动发生分岔而失稳；转速在380～490 rad/s区间时，系统响应表现为倍周期运动；转速在490～540 rad/s区间时，系统响应表现为周期运动；转速在540～650 rad/s 区间时，系统响应表现为概周期运动；转速在650～670 rad/s 区间时，系统响应表现为3 倍周期运动；转速在670～800 rad/s 区间时，系统相应表现为从概周期运动逐渐变成周期运动。

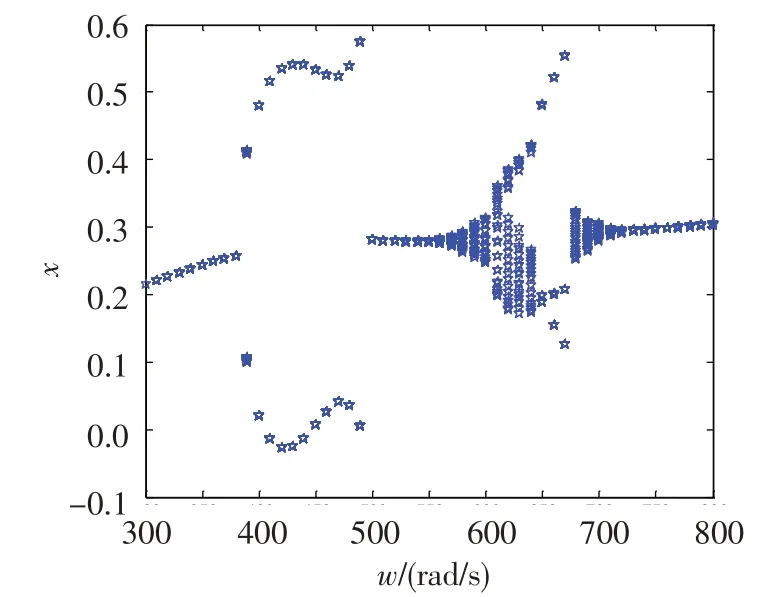
图12 轴承间隙为0.25 mm时的全局分岔图Fig.12 Global bifurcation diagram(c=0.25 mm)

图13给出了轴承间隙从0.20 mm增加至0.30 mm时，转子轴承系统在轴承间隙-转速参数域内的分岔集。可以看出，随着轴承间隙的增大，系统表现为倍周期分岔，分岔失稳转速不断降低。因此，在此类转子-轴承系统设计中，应该选择较小的轴承间隙。

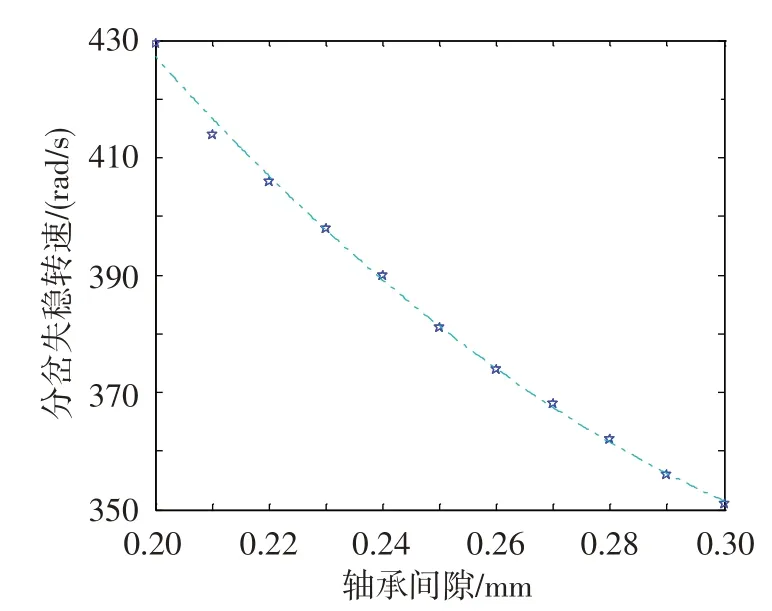
图13 转子轴承系统在轴承间隙-转速参数域内的分岔集Fig.13 Bifurcation set of bearing clearance-speed in the parameter domain of rotor system

4 结论

采用Poincare 映射方法得到转子系统的分岔图、轴心轨迹图、Poincare图、时间历程图和频谱图，从而得出分岔失稳转速随偏心量、轴承间隙、润滑油黏度3 个参数的变化规律。随着偏心量的增大，分岔失稳转速先减小后增大，存在最低分岔失稳转速；随着润滑油黏度的增大，系统的分岔失稳转速越来越高，稳定性越来越好；随着轴承间隙的增大，分岔失稳转速越来越低。滑动轴承-转子系统设计和运行时，应尽可能选择较小的轴承间隙和较大的润滑油黏度，并进行较高精度的动平衡，以提高系统的稳定性和安全性。