借助几何直观深化数学理解

□程希文

数学在本质上研究的是抽象了的东西，小学生的逻辑思维能力相对较弱，借助几何直观可以把复杂的数学问题变成简明、形象，有助于学生探索解决问题的思路，预测结果。几何直观是帮助学生理解抽象的数学知识，分析和解决数学问题的有效手段。

《义务教育数学课程标准（2022年版）》中提到“几何直观主要是指运用图表描述和分析问题的意识与习惯”。史宁中教授指出“几何直观就是依托、利用图形进行数学的思考和想象。它在本质上是一种通过图形所展开的想象能力”[1]。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。

几何直观可以使抽象的数学直观化，繁难的数学问题简洁化，有助于探索解决问题的思路和预测结果。因此，如何在“数与代数”教学中适切地渗透几何直观，让学生建立形与数的联系，构建数学问题的直观模型，利用图表分析实际情境与数学问题，探索解决问题的思路，这是一线教师应该深入思考的问题。笔者在“数与运算”“数量关系”教学中，借助几何直观，将相对抽象的思考对象“图形化”进行了尝试与实践。

一、在数的认识中渗透几何直观

数学学习心理学研究表明，儿童获得一个数学概念的过程是从动作表征过渡到图像表征，最后到符号表征。然而，抽象的数学结论总能找到相对直观的表征与解释。

（一）在认识自然数和分数时渗透几何直观

学生对直尺非常熟悉，在北师大版教材一年级上册“20以内数的认识”教学中，教师可以将直尺“抽象”为“数尺”来帮助学生理解自然数的大小与顺序（如图1）。

图1

在“数尺”上，抽象的“数”有顺序、有方向、有规律地排列，直观、形象地表示出来。学生在读数过程中发现：从左往右读时，数尺上的数由小到大；从右往左读时，数尺上的数由大到小；相邻的两数都相差1；在数尺上0是最小的数；离“0”越近的数越小，离“0”越远的数越大；最大的一位数是9，最小的两位数是10；等等。直观形象的“数尺”，不仅有助于帮助学生理解数的顺序、大小和数列的基本规律，也有助于学生体悟到数与“位置”的一一对应关系。

在分数的教学中，教师可以通过在同一条“数线”上呈现不同类型的分数来帮助学生直观理解等值的概念，同时还发现“数线”上的这些分数都比0大，比1小（如图2）。

图2

（二）在认识小数和负数时渗透几何直观

认识“小数”时，教师可以通过数轴、百格图等直观模型帮助学生加深对小数意义的理解。在练习环节，可以设计以下活动：1.用小数、分数分别表示百格图中涂色部分和空白部分的大小（如图3）；2.用小数或分数表示数轴上的指定位置（如图4）；3.在图中用阴影部分表示出小数（如图5）。通过数形结合的方法，可以有效地帮助学生理解、明晰抽象的数学概念，让深度学习自然发生。

图3

图4

图5

在学习“负数”时，可以通过“数轴”来促进学生对负数意义的深度理解。教师在黑板上先呈现数轴（如图6），然后引导学生：“如果笑笑家的位置用刻度‘0’来表示，笑笑从家向东走90米到达书店，可表示为+90米；那么笑笑从家向西走90米到达超市，可以表示为多少米，你能在图上用一个点表示出超市所在的位置吗？”

图6

学生能很快回答出笑笑从家向西走90米可以表示为－90米，但对于在图上用一个点来表示超市所在的位置时出现了不同的意见，有的学生认为这个点的位置只要是在“0”的左边就行，有的认为不可以随意找一个点来表示超市的位置。最后，大家通过讨论达成共识：在图上，从刻度+90到0的距离与从刻度－90到0的距离应该完全相等。这样，通过几何直观实现了学生对负数本质的理解：负数与对应的自然数在数量上相等，但表示的意义相反。

二、在数的运算中渗透几何直观

朱莉娅·安吉莱瑞认为，在使用符号计算的过程中，教师要鼓励学生使用尽可能多的解释，并且把不同表征形式联系起来。如果意识不到这一点，计算规则就会限制学生对数学的理解[2]。毋庸置疑，几何直观在运算教学中发挥着不可替代的作用。

（一）在整数四则运算中渗透几何直观

在北师大版教材一年级下册教学“两位数加两位数的进位加法”时，运用直观模型操作的方法就可以很好地帮助学生实现对“从个位算起”这一运算的程序的深度理解。如在计算“37+24”时，教师先让学生操作小棒并清楚地描述计算的过程，学生通常会有两种不同的方式，一种是先加十位再加个位，另一种是先加个位再加十位（如图7）。

图7

接着让学生把自己的操作过程记录下来，就得到了相应的竖式（如图8）。学生在操作、交流和记录的过程中体悟到：计算“37+24”时，可以先加十位也可以先加个位，而先加个位的优势就是比先加十位在书写时更简洁，不需要多次调整。这样，整个学习进程遵循了从直观到抽象的原则。

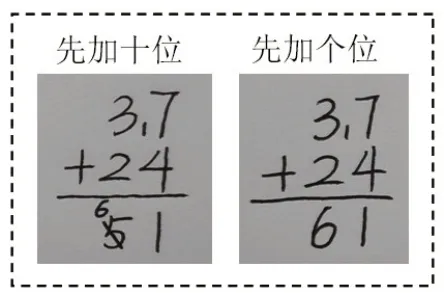
图8

通过研读北师大版教材可以发现，直观模型——“点子图”始终贯穿表内乘除法、一位数乘（除）两位数以及两位数乘两位数等计算教学内容当中。所以，教学中教师要充分利用“点子图”的操作性、直观性特点，帮助学生理解算理，掌握算法（如图9）。

图9

（二）在分数四则运算中渗透几何直观

学生学习分数计算比整数计算会困难很多，原因是分数的意义较难理解，而且分数四则运算的算理复杂，不容易解释，特别是“分数乘法”和“分数除法”的学习。运用几何直观的方式展现探索过程，解释算理就显得尤为重要。如计算时，可以鼓励学生用画图的方式表征计算过程（如图10）。在直观理解算理的基础上，教师再引导学生通过比较算式和结果数值的关系归纳出算法：两个分数相乘，只要分子乘分子，分母乘分母就可以了；能约分的可以先约分。

图10

分数除法对小学生来说则是更为抽象。教学中，如果仅仅让学生记住“颠倒相乘”的算法显然是不够的，而要借助直观图形的表征帮助学生对分数除法算理的理解。如计算时，既可以通过包含除的方式理解算理如图11），也可以通过均分的方式理解算理（如图12）。计算时，也同样可以让学生在直观中实现算理的深刻理解如图13）。在借助直观图形理解算理的基础上，教师再鼓励学生对计算方法进行大胆猜想，并顺势引导学生验证猜想的合理性进而转向符号操作，发展学生的推理能力。

图11

图12

图13

三、在解决问题中渗透几何直观

画图是解决问题的重要方法之一，运用画图法能使抽象复杂的数量关系变得简单明了，将抽象的数学问题直观化。所以，教师要重视学生画图技能的培养，让学生掌握一些必要的图形工具，如线段图、方格图以及常见的几何图形等。解决问题时，教师要鼓励学生尽量通过画图的方法帮助自己理解题意、分析数量关系、明确解题思路。

比如，线段图就可以使抽象的数量关系变得形象化和直观化。在解决下面这样的稍复杂百分数问题时，线段图在厘清数量关系方面的作用是显而易见的。

2000年笑笑家食品支出总额占家庭总支出的55%，其他支出总额占家庭总支出的45%，食品支出比其他支出多620元。笑笑家的家庭总支出是多少元？

由于题目中的数据较多，而“食品支出总额”“其他支出总额”以及“家庭总支出”都是未知数，学生不容易找到解题思路。这时，借助线段图不仅可以很好地帮助学生理解数量关系，还能够进一步明确和拓展解题思路（如图14）。

图14

画出线段图后，教师要引导学生借助图形多角度审视问题，厘清各数量之间的关系。如总支出×55%=食品支出，总支出×45%=其他支出，食品支出+其他支出=总支出，食品支出－其他支出=总支出的10%，总支出×10%=620元。学生既可以列方程解答，即设总支出为x元，列出方程：55%x－45%x=620；也可以用算术方法列式：620÷（55%-45%）=6200（元）。

同样，在解决下面这样的问题时，“画图”也可以发挥重要的作用。

将一个边长为20厘米的正方形纸，剪成4个完全一样的小正方形纸片，每个小正方形的周长是多少？

计算每个小正方形的周长时，不少学生这样列式：20×4÷4=20（厘米）。出错的原因是他们想当然地用大正方形周长平均分成4份来求小正方形的周长。学生借助几何直观，通过画图就可以变“看不见”为“看得见”，直观地看出4个小正方形的周长与大正方形周长的关系（如图15），正确的列式为：20÷2×4=40（厘米）。

图15

利用图形描述和分析问题，这里的问题不仅包括几何以外的问题，也包括几何问题本身，如利用图形的运动去认识和理解几何图形也是几何直观[3]。正因为几何直观渗透在数学的各个方面，教师在教学中就要善于挖掘和捕捉几何直观的资源，恰当地运用几何直观来解释和说明数学的内在道理，促进学生对数学知识的深度理解。当然，学生几何直观能力的培养并不是一蹴而就的，它需要教师在各种教学细节中有意地渗透，在日常课堂教学中坚持不懈、一以贯之地培养。