基于GRA-IFA-LSSVM模型的气田集输管道内腐蚀速率预测

周 阳,王寿喜

(西安石油大学,西安 710065)

目前,我国部分气田已经进入到开发后期阶段,这些集输管道的服役时间相对较长,介质中的含水率以及酸性物质含量随服役时间的延长不断提升,致使管道的腐蚀速率不断加快[1-4]。腐蚀是威胁管道运行安全的重要因素。因此,气田集输管道腐蚀速率的准确预测对提前制定防护措施、保障气田管道运行安全十分重要[2-6],同时也有利于推动我国能源产业的进一步发展。

国内外学者对于气田管道腐蚀速率预测进行了多方面的研究。骆正山等[7]通过建立随机森林算法,对凝析气田管道的腐蚀问题进行了全面研究,研究过程中使用灰色关联度算法对内腐蚀速率的影响因素进行了全面筛选,并使用气田集输管道实际腐蚀速率数据对所建立的模型进行了验证,但是随机森林算法在使用的过程中会出现过度拟合问题,最终导致预测结果精度降低。RAJU等[8]通过引入压电传感器的方式,对管道的腐蚀问题进行了全面评价,使用该种方法的腐蚀速率评价结果相对精度较高,但是所需要的经济成本也相对较高,同时压电传感器非常容易受到腐蚀的影响出现损坏问题。曾维国等[9]建立了径向基神经网络模型进行腐蚀速率研究,在模型训练过程中,其预测值与期望值之间的相关性相对较高,使用该种模型可以对腐蚀风险相对较高的管道进行筛选,但是神经网络类型的算法对于样本数量的依赖度相对较高,在训练样本相对较少的前提下,预测结果将会受到较大的影响。梁金禄等[10]针对高含硫气田的腐蚀问题,使用PSO(粒子群优化)模型对SVM(支持向量机)模型中的参数进行了优选,然后使用SVM模型进行了腐蚀速率研究,预测结果显示,该种模型的预测误差相对较小,但是在使用PSO对参数进行筛选的过程中,非常容易出现局部最优的问题,即优选的参数可能不是最佳参数。

通过全面调研发现,目前国内外关于管道腐蚀速率预测的研究存在一定的局限性。为此,本工作将使用灰色关联度(GRA)模型对气田集输管道内腐蚀的影响因素进行全面筛选。萤火虫(FA)模型非常容易出现局部最优的问题,因此,对其进行了改进,得到改进后的萤火虫(IFA)模型。最小二乘支持向量机(LSSVM)模型中两种参数的设定会对预测结果产生影响,因此,使用IFA模型对LSSVM模型进行了参数优选,最终建立GRA-IFA-LSSVM模型,对气田集输管道的内腐蚀速率问题进行预测研究,为保障气田集输管道的安全运行奠定基础。

1 理论基础

1.1 GRA模型

对于灰色关联度(GRA)模型而言,其属于一种根据系统的发展趋势进行定量分析以及比较的算法[11]。使用GRA算法的过程可分为以下5个步骤。

(1) 确定母序列与子序列之间的关系。在进行气田集输管道内腐蚀速率预测的过程中,将介质的温度、流速、H2S含量、CO2含量、O2含量、水含量、盐含量以及pH作为其影响因素,此时的母序列可以表示为:X0={x0(1),x0(2),…,x0(m)}。对于第i个子序列而言,可以表示为:Xi={xi(1),xi(2),…,xi(m)}(i=1,2,3,…,8),最终可以构成式(1)所示矩阵。

(1)

(2) 对数据进行处理。由于各个影响因素数据以及腐蚀速率数据量纲之间存在较大的差异,因此，数值的差异度相对较大,需要对其进行初值变换处理,得到式(2)。

(2)

式中:X0为数列后面的数据;X0(1)为某一列数据的第一个数值;Y0为处理后得到的数据。

初值变换处理后的第i个子序列,可表示为式(3)。

(3)

在进行无量纲处理以后,可以得到如式(4)所示矩阵。

(4)

(3) 对Yi和Y0之间的关联系数σ0i进行计算,见式(5)。

(5)

式中:ρ为分辨系数,其处于区间[0,1]内,一般可以取值0.5。

(4) 对所有影响因素的关联度进行处理,此时可以得到Yi对Y0的关联度γ0i,如式(6)所示。

(6)

式中:M为数据数量。

(5) 对所有影响因素的关联度γ0i进行排序,对较为重要的影响因素进行筛选[12]。

1.2 IFA模型

萤火虫(FA)模型是一种相对较为先进的参数优选算法,在整个种群中,每一个萤火虫都代表一个数值解,其相对亮度表示适应度,根据其相对亮度可以确定每个个体的位置移动方向,亮度较小的个体将会向亮度大的个体移动,而最亮的个体,会随机移动[13-14]。使用该种类型算法的步骤如下:

(1) 对各个参数进行初始化处理,计算每个个体的初始化相对亮度I0。

(2) 根据式(7)、(8)、(9)对I和β进行计算。

(7)

(8)

(9)

式中:β为吸引力数值;β0为最大吸引力数值;I为个体的相对亮度;I0为个体的初始化相对亮度;γ为光吸收系数数值;rij为个体i和个体j之间的距离;d为空间维数,根据优化运算的目标确定;xi,k为个体i的第k个数值。

(3) 根据式(10)对个体的位置进行更新。

xi(t+1)=xi(t)+
β[xj(t)-xi(t)]+α(rand-0.5)

(10)

式中:xi,xj分别为个体i和个体j所处的位置;α为随机步长,其处于区间[0,1]中;rand函数表示在区间[0,1]内产生随机实数。

(4) 确定位置更新以后个体的亮度。

(5) 若满足所有的条件,输出最佳的极值,结束;若不满足条件,需要从步骤(3)开始重新迭代。

在FA算法的使用过程中,非常容易出现局部最优的问题,同时如果参数设置不合理,还可能会出现函数无法收敛的问题。因此,需要对其进行合理的改进,改进后的萤火虫(IFA)算法为:

(1) 对每个个体的位置进行Logistics混沌初始化处理,进而使得种群多样性得到提升,全局搜索能力得到增强,Logistics混沌处理的映射公式见式(11)。

zn+1=rzn(1-zn)

(11)

式中:r为混沌因子,在取值为4的前提下,表示完全混沌,此时满足公式zn+1∈(1-zn)。

(2) 对于线性递减过程中的惯性权重w而言,其变化情况与迭代次数T以及最大迭代次数Tmax之间具有很强的联系,在进入到后期阶段后,其收敛的速度将会大幅降低,进而出现局部最优的问题。针对该问题,本工作引入一种新的惯性权重计算方法,如式(12)～(13)所示。该计算方法基于每个个体以及整体的适应度数值,适应度fi如式(14)所示,IFA算法位置更新如式(15)所示。

(12)

(13)

(14)

xi(t+1)=w(t)xi(t)+
β[xj(t)-xi(t)]+α(rand-0.5)

(15)

1.3 LSSVM模型

LSSVM模型属于一种对SVM(支持向量机)进行改进的算法,使用该算法时,在对偶空间之内,不等式可以使用等式进行约束。同时,可以根据最小二乘基本理论,对损失函数进行合理优化。最终将二次规划问题转化为方程组的求解问题。此时使用该模型进行数据预测的精度进度得到大幅提升[18-20]。LSSVM算法的应用步骤为:

(1) 将数据集合分为两个样本组,分别是训练样本以及预测样本,训练样本可以表示为D={(xi,yi)|i=1,2,…,n},其中,xi∈Rn为第i个样本,yi∈{-1,+1}输出数据组合。

(2) 在高维空间之内,可以将回归函数表示为式(16)。

y(x)=ω·φ(x)+b

(16)

式中:ω为可调权函数;φ(x)为映射函数;b为偏差参数。

(3) 在对参数ω和b进行求解的过程中,需要引入结构风险最小化理论,求解公式如式(17)所示。

(17)

式中:C为正则化参数;ξi为误差。

(4) 为了实现最优的目标,引入拉格朗日函数进行求解,如式(18)所示。

(18)

式中:αi为乘子,使用L(ω,b,ξ,α)对ω,b,ξ,α进行偏微分求解,进而得到式(19)。

(19)

(5) 将上述公式中的参数ω和ξi去除,并将式(19)转化为矩阵

(20)

式中:e=[1,1,…,1]T,y=[y1,y2,…,yn]T,α=[α1,α2,…,αn]T,Ωij=φ(xi)·φ(xj)=k(xi,xj)。k(xi,xj)为核函数矩阵,本工作中使用的核函数为径向基函数,如式(21)所示。

(21)

(6) 对上述方程进行求解,最终得到线性方程

(22)

在使用LSSVM算法时,正则化参数C以及径向基函数中的参数σ会对最终的预测结果产生重要影响,为了全面降低内腐蚀速率预测的误差,使用改进的萤火虫算法对参数进行优选[21-23]。

2 气田集输管道腐蚀速率预测模型的建立

2.1 GRA-IFA-LSSVM组合模型建立流程

按图1所示流程建立预测气田集输管道内腐蚀速率的GRA-IFA-LSSVM组合模型。

图1 GRA-IFA-LSSVM组合模型建立流程Fig.1 Process of building GRA-IFA-LSSVM combined model

(1) 引入灰色关联度算法,对气田集输管道内腐蚀速率的影响因素进行筛选,确定内腐蚀的主要影响因素。

(2) 引入萤火虫算法,对初始参数进行设置。

(3) 根据式(11)产生混沌序列,将其作为萤火虫算法使用过程中的初始种群。

(4) 对适应度进行计算,使用LSSVM模型对训练数据集合进行学习,并对预测数据集的预测误差进行计算,将每个萤火虫的绝对百分比误差作为IFA算法使用过程中的适应度,如式(23)所示。

(23)

式中:Ai为实际值;Pi为预测值。

(5) 根据式(8)和式(9)对IFA算法进行计算,对每个个体之间的距离以及步长进行判断,使用式(10)和式(15)对每个个体的位置进行更新。

(6) 对适应度进行重新计算,使用式(11)和式(12)进行混沌序列优化以及搜素。

(7) 输出最佳参数至LSSVM模型中,使用LSSVM模型对训练数据集进行学习,对预测数据集进行预测。

2.2 模型评价指标

为了对GRA-IFA-LSSVM组合模型的预测精度进行全面评价,引入三种误差评价方法,分别是均方根误差ERMSE、平均相对误差EMRE以及可决系数R2,三种评价方法的计算公式分别如式(24)～(26)所示。

(24)

(25)

(26)

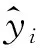
3 实例应用

3.1 样本数据

为了对本研究所提出的GRA-IFA-LSSVM组合模型进行验证,以我国某气田为例,进行了集输管道腐蚀试验。该气田集输管道的材料为16Mn钢,随着管道使用时间逐渐增长,腐蚀已经成为威胁管道安全运行的重要因素。在研究的过程中,采用腐蚀挂片的方式对腐蚀样本进行提取。腐蚀挂片的尺寸为10 mm×3 mm×50 mm,采样周期为30 d,取出的挂片经清水冲洗、防锈剂浸泡以及无水乙醇处理等步骤后吹干,然后进行了称量。根据挂片腐蚀前后质量变化计算腐蚀速率,如式(27)所示。

(27)

式中:vcorr为腐蚀速率,mm/a;K为换算系数,8.76×104;Δγ为挂片腐蚀前后质量差,g;t为时间,d;μ为材料密度,g/cm3;S为挂片的表面积,cm2。经过试验,共获取76组数据,部分数据如表1所示。

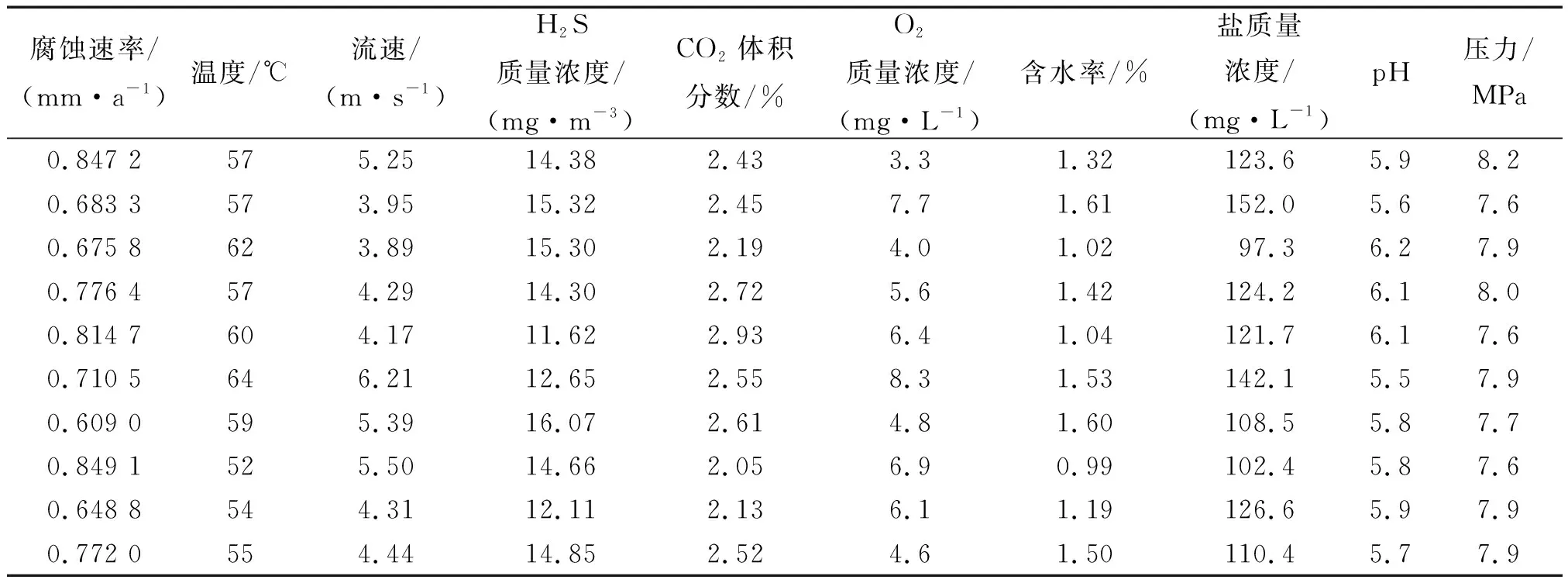
表1 部分腐蚀速率及影响因素数据Tab.1 Partial data of corrosion rates and influencing factors

3.2 特征指标及参数确定

根据GRA算法的计算步骤,计算各影响因数与腐蚀速率的关联度，结果如表2所示。分析表2中数据可以发现,每种影响因素与管道腐蚀速率的关联度数值都相对较高。本研究将选择关联度数值较高的前五项作为模型的特征变量,腐蚀速率作为模型的输出目标。这五项影响因素分别为温度、H2S含量、CO2含量、pH以及流速。

表2 影响因素关联度计算结果Tab.2 Calculation results of correlation degree of influencing factors

为了对本研究所提出的GRA-IFA-LSSVM组合模型进行先进性验证,将其与FA-LSSVM算法、GA-LSSVM算法(遗传算法优化最小二乘支持向量机)以及PSO-LSSVM(粒子群算法优化最小二乘支持向量机)算法进行对比。在使用IFA算法以及FA算法的过程中,种群规模设定为30,步长因子设定为0.1,光吸收强度设定为1,最大吸引度设定为1,最大迭代次数设定为100,训练精度设定为10-6。在使用GA算法的过程中,种群规模设定为30,最大迭代次数设定为100,训练精度设定为10-6,交叉概率设定为0.6,突变概率设定为0.05。在使用PSO算法的过程中,种群规模设定为30,粒子群维数设定为2,惯性权重设定为0.4,学习因子设定为0.2,最大迭代次数设定为100,训练精度设定为10-6。使用4种算法分别对LSSVM模型中的正则化参数C以及径向基函数参数σ进行优选,得到的参数数值如表3所示,将这些参数数值分别输入LSSVM算法中,进行腐蚀速率预测。

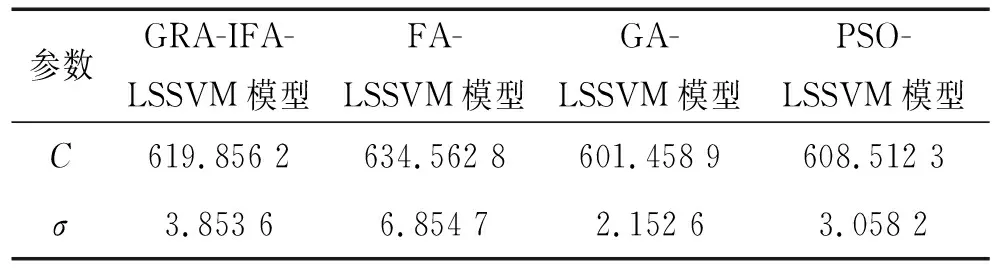
表3 参数优选结果Tab.3 Results of parameter optimization

3.3 结果分析与模型对比

将76组数据分为两组,训练数据组以及预测数据组。训练数据组为66组气田集输管道腐蚀速率及影响因素数据,用于GRA-IFA-LSSVM、FA-LSSVM、GA-LSSVM以及PSO-LSSVM模型训练;预测数据组有10组,用于模型验证。采用训练数据组对4种模型进行训练后，再根据预测数据组数据进行预测,预测结果如表4、图2及图3所示。通过对预测结果进行分析可以发现:GA-LSSVM模型的预测精度最差,其最大相对误差达到了21.454 7%,平均相对误差达到了9.500 8%; GRA-IFA-LSSVM模型的预测精度最好,其预测结果的最大相对误差为2.919 1%,最小相对误差为1.012 3%,该模型的误差区间为[1.012 3%, 2.919 1%];PSO-LSSVM模型的误差区间为[2.860 8%,9.115 5%],FA-LSSVM模型的误差区间为[2.014 5%,17.281 8%],相比之下,GRA-IFA-LSSVM模型的误差区间较小,取值范围也相对较小。对图2进行分析可以发现,本研究所提出的GRA-IFA-LSSVM组合模型的预测结果与实际腐蚀速率相对较为接近,相对误差变化相对平稳,证明该模型的鲁棒性较强,因此,GRA-IFA-LSSVM组合模型优于其他三种模型,适用于气田集输管道内腐蚀速率预测。

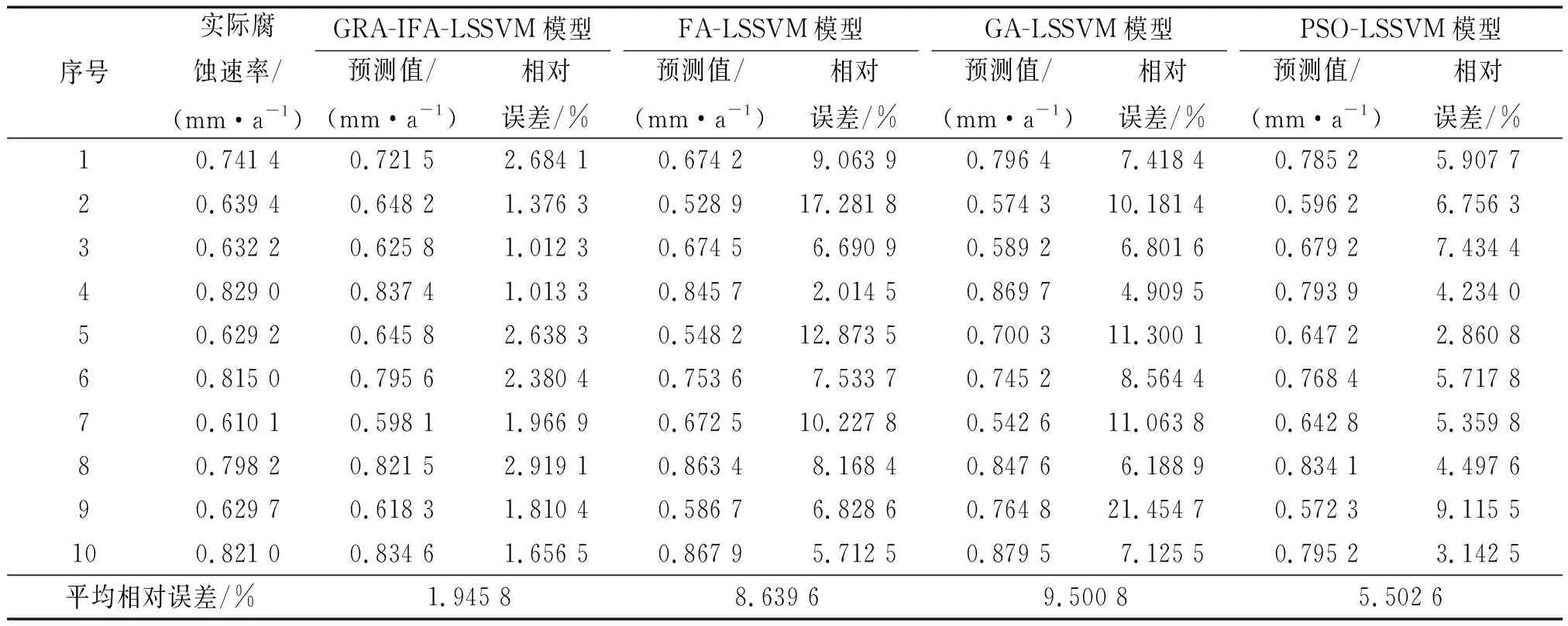
表4 4种模型的预测结果Tab.4 Prediction results of four models

图2 4种模型预测结果与实际腐蚀速率对比Fig.2 Comparison of prediction results of four models and actual corrosion rate

图3 4种模型预测误差对比Fig.3 Comparison of prediction errors of four models

分别将GRA-IFA-LSSVM、FA-LSSVM、GA-LSSVM以及PSO-LSSVM模型的预测结果与实际腐蚀速率进行相关性分析,结果如图4～7所示。由图4～7可以发现,GRA-IFA-LSSVM模型的R2为0.975 3,FA-LSSVM模型的R2为74.39,GA-LSSVM模型的R2为67.53,PSO-LSSVM模型的R2为81.08。其中,GRA-IFA-LSSVM模型的R2最为接近1,说明用GRA-IFA-LSSVM模型对气田集输管道内腐蚀速率预测具有很强的准确性以及鲁棒性。

图4 GRA-IFA-LSSVM模型预测结果线性拟合图Fig.4 Linear fitting diagram of IFA-LSSVM model prediction results

图5 FA-LSSVM模型预测结果线性拟合图Fig.5 Linear fitting diagram of FA-LSSVM model prediction results

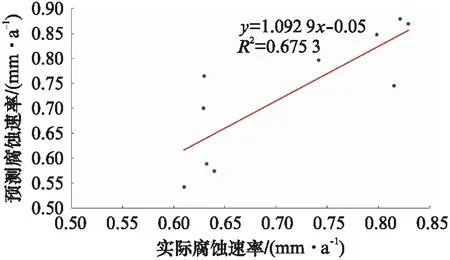
图6 GA-LSSVM模型预测结果线性拟合图Fig.6 Linear fitting diagram of GA-LSSVM model prediction results

图7 PSO-LSSVM模型预测结果线性拟合图Fig.7 Linear fitting diagram of PSO-LSSVM model prediction results

为了进一步对GRA-IFA-LSSVM组合模型进行验证,使用2.2节中的方法对模型进行评价,评价结果如图8所示。分析图8中数据可以发现,在用GRA-IFA-LSSVM模型进行气田集输管道内腐蚀速率预测的过程中,其平均相对误差为1.946%,均方根误差为1.496%,可决系数为0.975 3,这三项指标均小于其他模型。因此,在气田集输管道内腐蚀速率预测过程中,本研究提出的GRA-IFA-LSSVM组合模型具有很强的准确性、鲁棒性以及先进性,可以在气田集输管道腐蚀速率预测的过程中推广使用该种类型的方法。

图8 误差分析Fig.8 Error analysis

4 结论

(1) 在使用FA模型对LSSVM模型进行参数寻优的过程中,非常容易陷入局部最优的问题,因此,需要对其进行改进。对于IFA模型而言,其引入了新的惯性权重计算措施,同时,在对萤火虫个体的位置进行初始化时,引入了Logistics混沌初始化方法,可以避免出现参数优选过程中的局部最优问题。

(2) 在进行腐蚀速率预测时,如果将所有影响因素都输入到预测模型中,将会使得模型的复杂性提升,通过使用GRA算法对影响因素进行简化发现,温度、H2S含量、CO2含量、pH以及流速属于气田集输管道内腐蚀的主要影响因素,可以使用这五项影响因素代替所有影响因素输入到预测模型中进行腐蚀速率预测。

(3) 通过本研究所提出的GRA-IFA-LSSVM组合模型对气田集输管道内腐蚀速率进行预测,其平均相对误差为1.946%,均方根误差为1.496%,可决系数为0.975 3,这3项指标均小于其他模型,相对误差的变化也相对较小,证明该模型具有很强的准确性、鲁棒性以及先进性,可以在我国气田中推广使用。