基于事件触发的AUVs 固定时间编队控制

王洪斌 高 静 苏 博 王跃灵

随着海洋科学技术的进步,自主水下航行器(Autonomous underwater vehicle,AUV)在各种水下作业得到广泛应用,如在海底探测、地形测绘和水下施工等[1-5].在复杂作业环境下,需要多AUVs协同作业,提升作业效率,实现性能和指标,对一致性和编队控制则提出更高的要求.其中多AUVs 编队控制因具有作业范围广、效率高、容错性好等特点成为AUVs 系统重点研究方向.常用编队协调控制方法有领航者-跟随者法[6-8]、虚拟结构法[9]和基于行为控制法[10]等,其中领航者-跟随者法因其控制简单、编队队形结构实现难度低等优点,备受科研人员青睐.此方法是在多AUVs 编队系统中指定其中某个AUV 为领航者,其他AUVs 则为跟随者,领航者跟踪预先设定的参考轨迹,每个跟随者依据和领航者之间的位置误差和速度误差设计控制律,以一定的间隔距离与角度跟踪领航者,从而实现期望的编队目标.

多AUVs 编队控制是一项具有挑战性的工作.一方面,因其系统受限于有限的通信资源,传统连续时间通信会导致通信资源和能量的浪费.为了有效的利用通信资源,事件触发通讯机制[11-12]运用而生.事件触发控制是指只有当单个智能体的某一个状态变化量超过给定阈值时,该智能体被触发并与邻居进行信息传输,此方法能减少系统能耗和控制器的更新次数.文献[11]针对具有外部干扰的线性多智能体系统,提出一种分布式事件触发一致性协议,有效地减轻整个通信网络的通信负担.文献[12]讨论了高阶多智能体系统在外部扰动作用下的时变编队问题,提出一种事件触发积分滑模控制策略,节约了能耗,且避免触发时间序列的Zeno 行为.文献[13]针对一类非严格反馈的多智能体系统一致性跟踪问题,在考虑全状态约束和指定性能的基础上提出了一种事件触发自适应控制算法.

另一方面,编队的收敛速度是多AUVs 编队控制中的一个重要性能指标.理想的编队控制应在足够短的有限时间内完成所需编队.由于多数AUVs编队控制是渐近稳定的,基于收敛率的问题,有限时间[14-16]编队控制的研究提高了系统的收敛速度.文献[14]研究了基于有限时间扩张状态观测器的水面船舶分布式编队控制问题.文献[15]考虑具有视线范围和角度约束的自主水面船舶编队问题,提出了一种容错有限时间领航-跟随编队控制方案.文献[16]针对存在模型不确定性和环境扰动的欠驱动无人水面船舶编队问题,提出一种自适应有限时间扰动观测器,在有限时间内达到既定的编队目标.基于有限时间的编队控制提高了编队收敛速度,但其收敛时间取决于系统的初始状态,而初始状态在实际工程中随机变化,造成编队的收敛时间的不确定性.固定时间稳定理论[17-21]不仅可以提高系统收敛速度,而且其编队系统的收敛时间与初始状态无关,仅取决于控制器的设计参数,所以基于固定时间理论的控制器更符合实际系统.

本文同时考虑多AUVs 系统受限于有限的通信资源以及编队收敛速度慢等问题,提出一种基于事件触发的AUVs 固定时间编队控制方法.将分布式事件触发机制引入多AUVs 编队控制研究中,并且基于固定时间稳定构造出触发函数,设计出基于事件触发的编队控制器,保证系统全局固定时间有界性收敛,且收敛时间不受初始状态的影响,既加快系统的收敛速度,又通过降低控制器的触发频次和通信次数,提高对有限通信资源利用率,节约系统通信能量,同时证明无Zeno 行为;此外,在反步法中引入动态面技术避免了 “微分爆炸”问题,降低了控制器的复杂性.

1 问题描述

1.1 系统模型与假设

由2 个网络结构组成的AUV 队列,如图1 所示.每个跟随AUV 都配备一个传感器来接收相对位置和姿态信息.

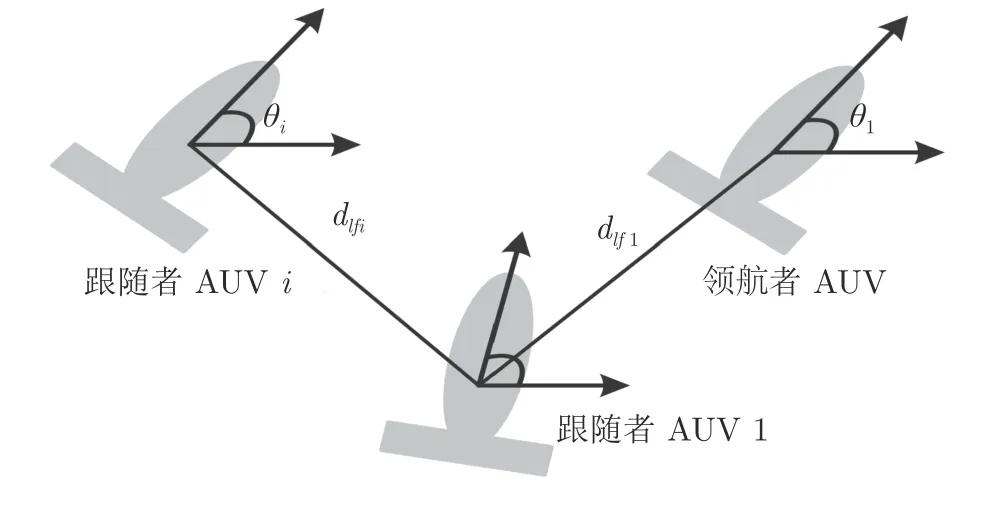
图1 领航-跟随多AUVs 编队示意图Fig.1 The diagram of leader-follower formation of AUVs

假设所有AUV 都有固定的姿态,则第i个AUV的水平面运动学及动力学模型[22]为:

控制目标: 在假设1 下,对于模型(1),基于反步动态面控制算法、固定时间控制理论和分布式事件触发通讯机制为跟随AUV 设计编队控制律,使跟随AUV 在安全距离内跟踪上领航AUV 的轨迹,完成编队控制目标,同时保证所有闭环信号达到全局固定时间稳定,即:

1.2 相关引理

引理1[21].考虑如下系统x∈Rn:

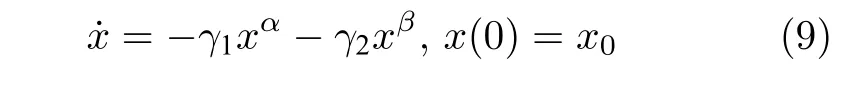
式中,γ1、γ2、α、β均是正常数,0＜α ＜1,β＞1.故系统在平衡点固定时间稳定的,其收敛时间T有界且不依赖于系统的初始状态,T满足不等式:

则系统是全局固定时间稳定的,且收敛时间T满足不等式(10).

3)若任意的x(t)满足不等式:

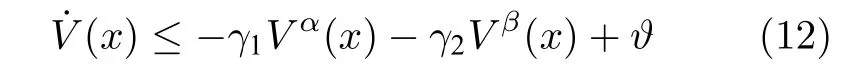
则该系统是实际固定时间稳定的,且存在正常数θ,0＜θ ＜1,使得收敛时间T满足:

2 主要结果

本节基于反步动态面控制算法,将分布式事件触发控制策略引入到多AUVs 编队控制策略中,设计编队控制器,同时选择合适的触发函数,保证系统达到全局固定时间稳定,实现期望编队控制的目标,其控制框图如图2 所示.

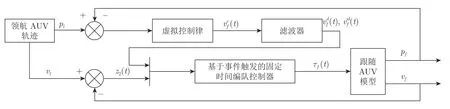
图2 编队跟踪控制示意图Fig.2 The diagram of formation control

2.1 事件触发编队控制器的设计

考虑到多AUVs 系统受限于有限带宽和有限通信资源,基于反步动态面算法思想,构造分布式事件触发机制,对于每个跟随AUV 给出基于状态信息的触发条件,当状态误差满足触发条件时才被触发,有效地减少控制器更新频率,降低通信资源的浪费.

用t0,t1,···来表示事件触发时间序列,其中tk表示跟随AUV 的触发时间.控制器设计如下:

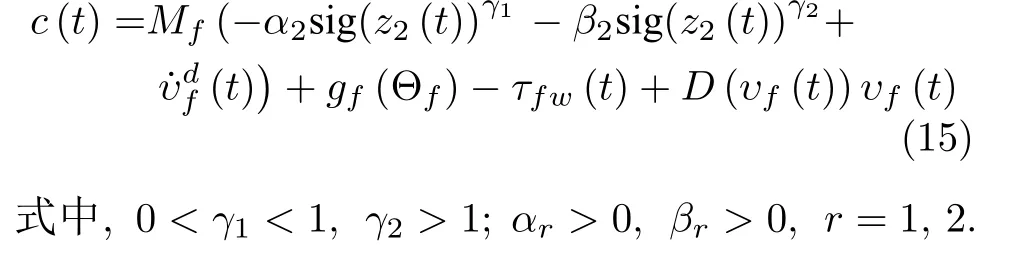
将事件触发机制定义为:

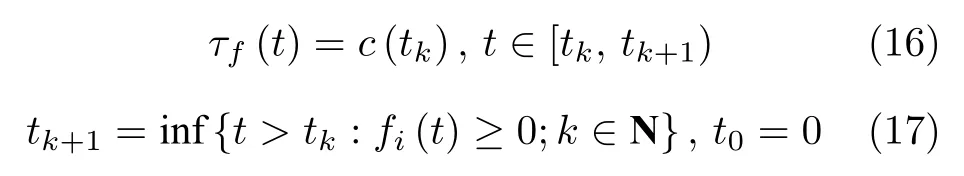
式中,fi(t) 为触发函数.当tk到达时,fi(t)≥0,事件触发控制器(17)被触发更新.在两次触发时刻之间,控制器保持不变.

将测量误差定义为:

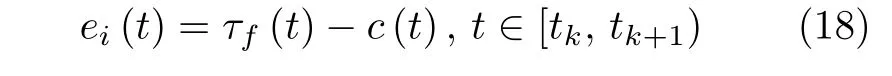
在领航-跟随编队控制策略、反步动态面控制算法和李雅普诺夫理论的基础上,利用固定时间理论,基于事件触发的编队控制器的设计过程分2 步.

步骤1.定义位置跟踪误差为:

为了验证z1(t)的收敛性,构造如下正定的李雅普诺夫函数:

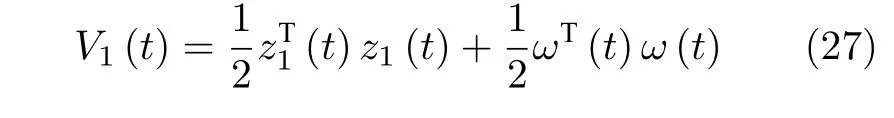
结合式(25)～ (26)、假设1 和Young's 不等式,对其求导,可得:

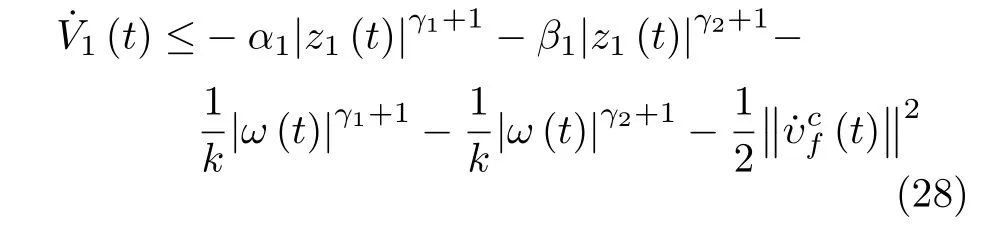
进一步可得:

由引理1～ 2,可得系统z1(t)是固定时间稳定的.

步骤2.定义速度跟踪误差:

由式(33)和定义1 对V2(t)求导,并依据假设1 和Young's 不等式,可得:

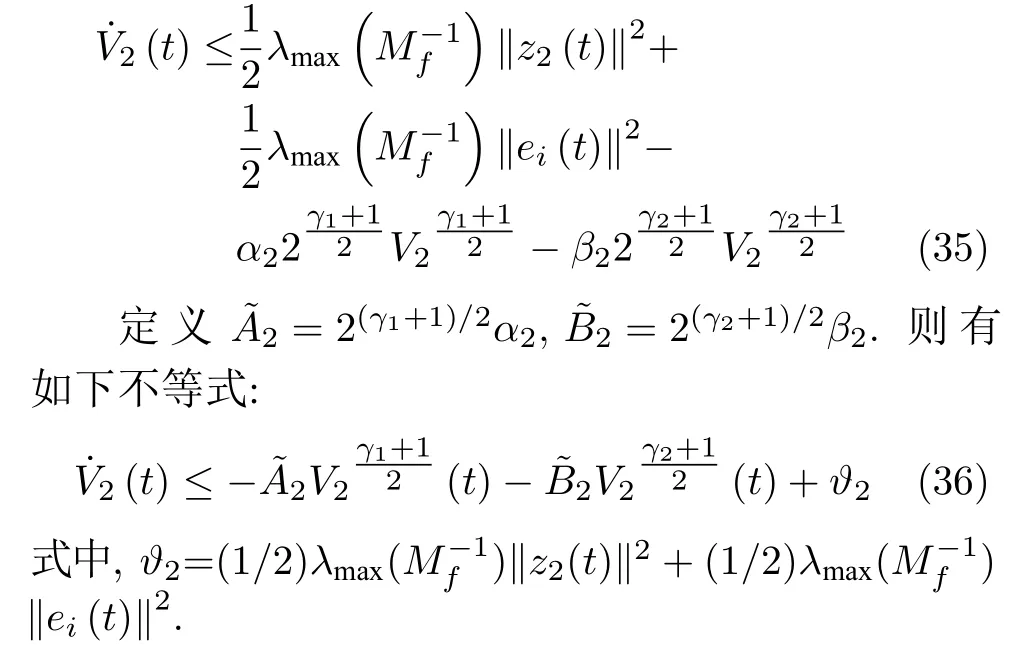
综上,根据引理2,可得系统z2(t)是固定时间稳定的.

定理1.考虑被控对象式(1),满足假设1 条件下,将分布式事件触发控制引入AUVs 编队控制策略中,设计出基于事件触发的控制器式(16),将触发函数选择为:

证明.为了验证整个多AUVs 编队控制系统稳定性,构造如下李雅普诺夫函数:

综合式(25)～ (26)和式(33),对V(t)求导,并依据Young's 不等式和定义1,可得:

2.2 可行性分析

事件触发通讯机制的关键是排除Zeno 行为,若存在Zeno 行为会使其控制器被无限次触发,通过证明任意两次触发间隔{tk+1-tk,k ∈N}都存在一个正下界,即可说明事件触发过程无Zeno 行为.

定理2.考虑多AUVs 编队系统(1),根据假设2,对于任意的初始状态,在事件触发控制器(16)和触发条件(37)作用下,以任意两次触发时刻为端点的区间段,其区间长度{tk+1-tk,k ∈N}一定存在某一固定的正下界.

根据式(18)、式(22)、式(33)和假设2,得到如下不等式:

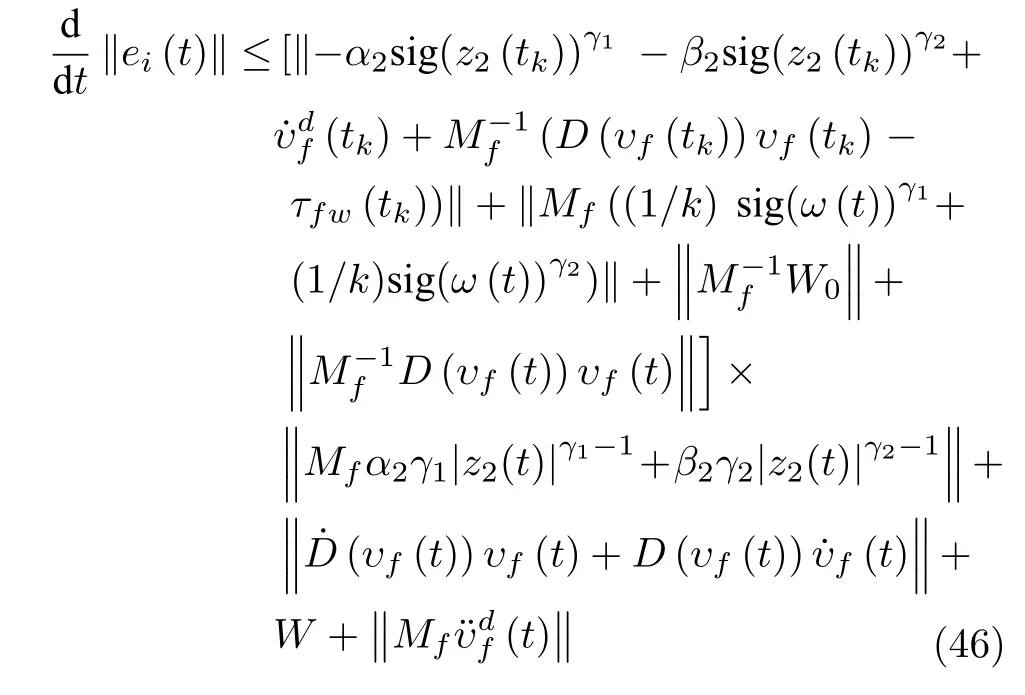
由式(27)和式(34)中正定的李雅普诺夫函数,可得不等式:

3 仿真研究

为了说明本文提出的控制方法的有效性,本文对4 艘AUV 组成的系统进行编队控制的仿真研究.

3.1 仿真条件

3.2 仿真结果

3.2.1 本文算法的仿真实例

为了验证本文提出编队控制策略的有效性和合理性,在相同条件下对两种工况(见表1)进行仿真验证,区别在于工况1 和工况2 取值于任意不同初始状态.其中AUV 0、AUV 1、AUV 2 和AUV 3 代表1 个领航者和3 个跟随者.控制器参数选择如下:k=diag{30,30,30},α1=β1=0.01,α2=2,β2=80,γ1=0.7,γ2=1.1.

工况1.依据本文提算法及上述参数对工况1中不同初始状态(见表1) 进行仿真,仿真结果如图3～ 12 所示.

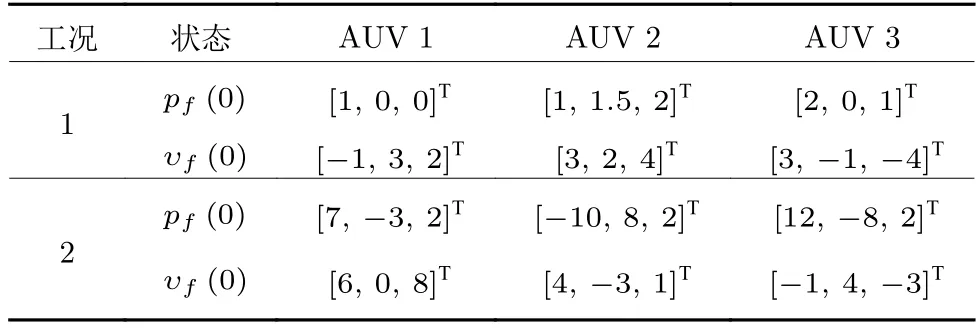
表1 跟随 AUVs 的任意初始状态Table 1 The arbitrary initial state of AUVs

图3 为多AUVs 的运动轨迹,显然在所提出的事件触发编队控制律下,跟随AUV 在安全距离内跟踪上领航AUV,实现所需的编队目标.图4～ 5分别为每个运动方向上位置状态和位置跟踪误差z1(t),z1(t)很好地收敛到原点附近.图6～ 7 为速度跟踪效果及其误差z2(t),可以看出,在事件触发编队控制器作用下,2 秒内所有跟随AUVs 的速度很好地跟踪上领航AUV 的速度,达到期望的收敛效果和控制精度.图8～ 9 分别为跟随AUVs 的虚拟控制器(t) 和控制输入向量τf(t).图10 给出在工况1 下所有跟随AUVs 的事件触发时刻示意图,可以看出,每个AUV 的事件触发时刻不在同一时刻,验证了本文设计的触发机制是分布式的,从而降低网络通信负担.此外,为了更加直观说明引入事件触发机制节约了通信资源,将工况1 下所有跟随AUVs 的触发次数统计结果在后续表2 中给出并进行分析.

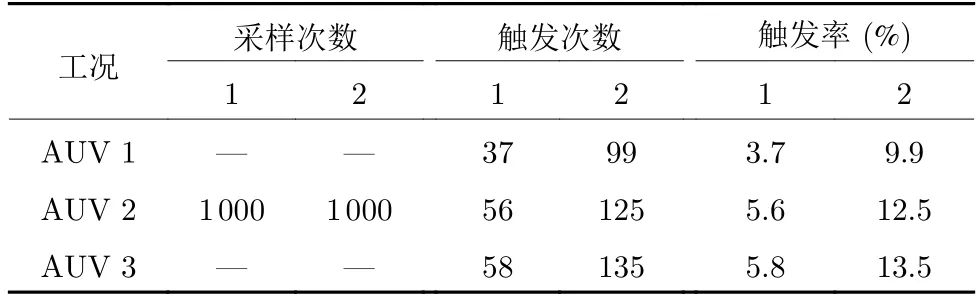
表2 跟随者AUVs 的事件触发次数和触发率Table 2 Event-triggered and triggered ratios for follower AUVs

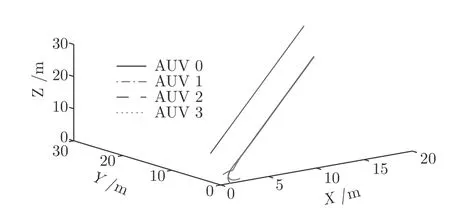
图3 工况 1 下的轨迹Fig.3 The trajectory under working Condition 1

图4 工况 1 下的位置Fig.4 The position under working Condition 1

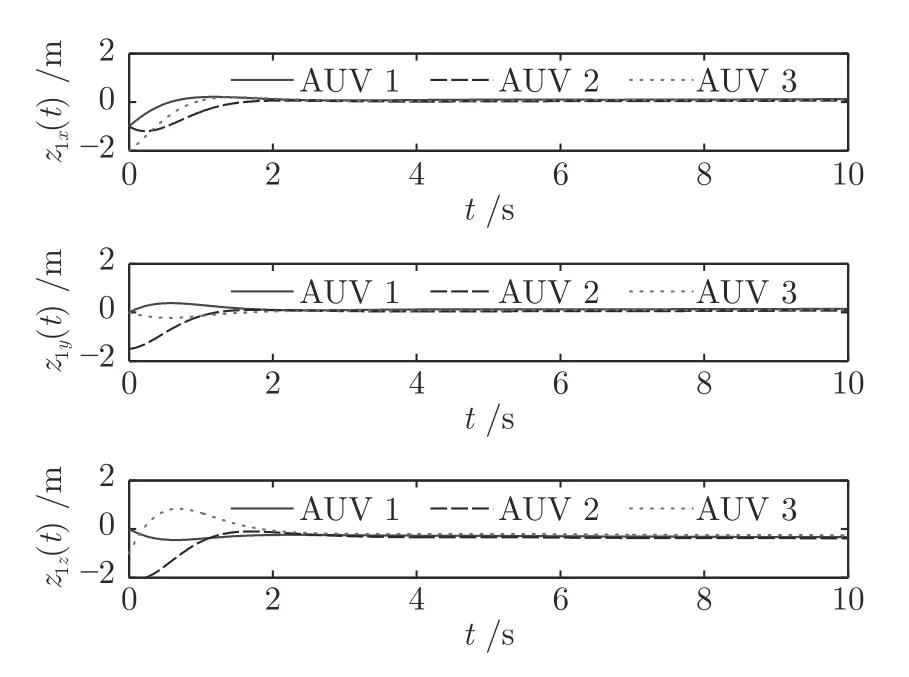
图5 工况 1 下的位置跟踪误差Fig.5 The position tracking error under working Condition 1

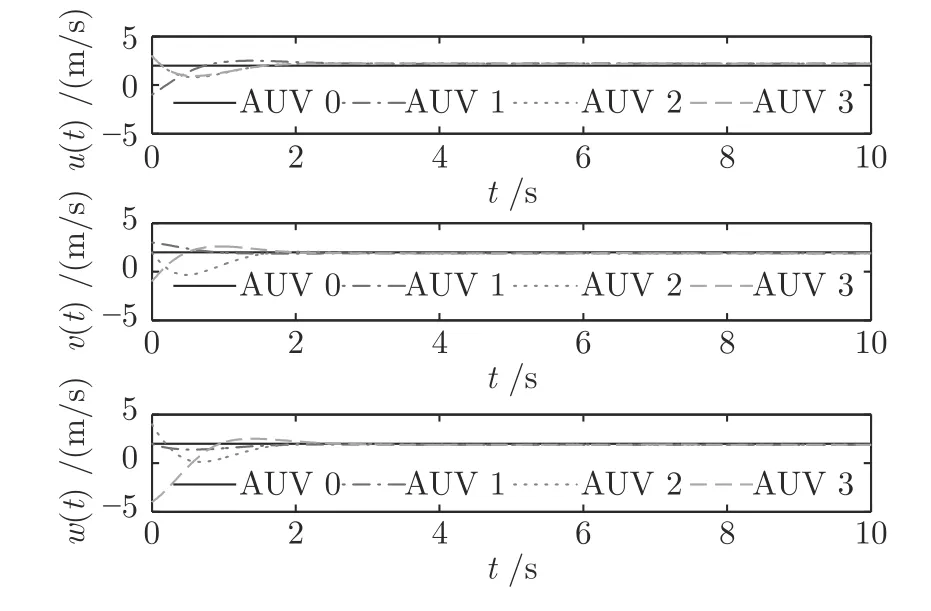
图6 工况 1 下的速度Fig.6 The velocity under working Condition 1

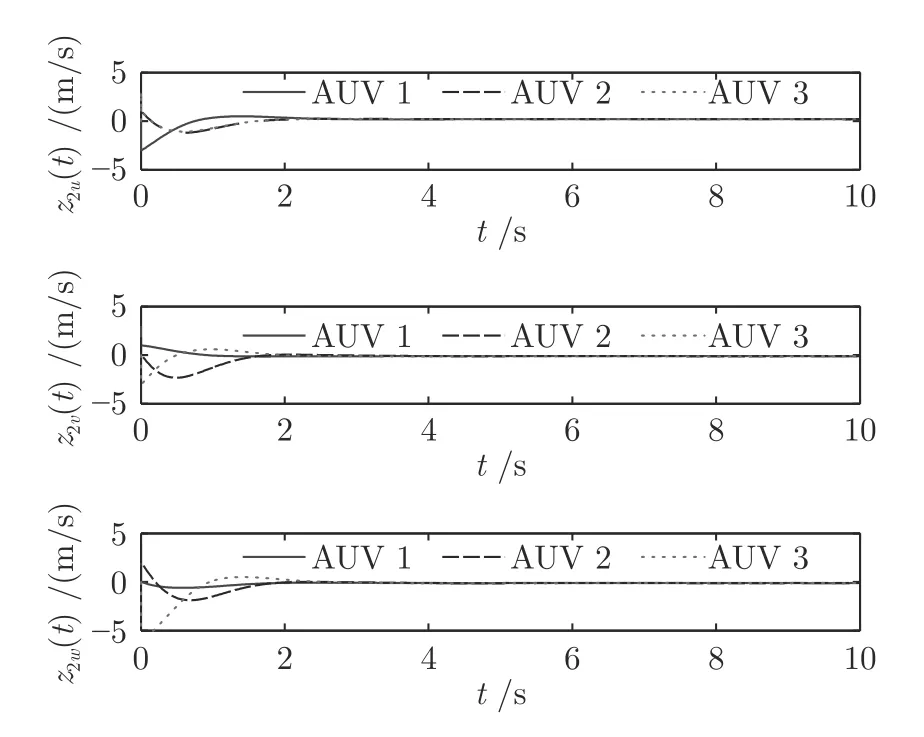
图7 工况 1 下速度跟踪误差Fig.7 The velocity tracking error under working Condition 1

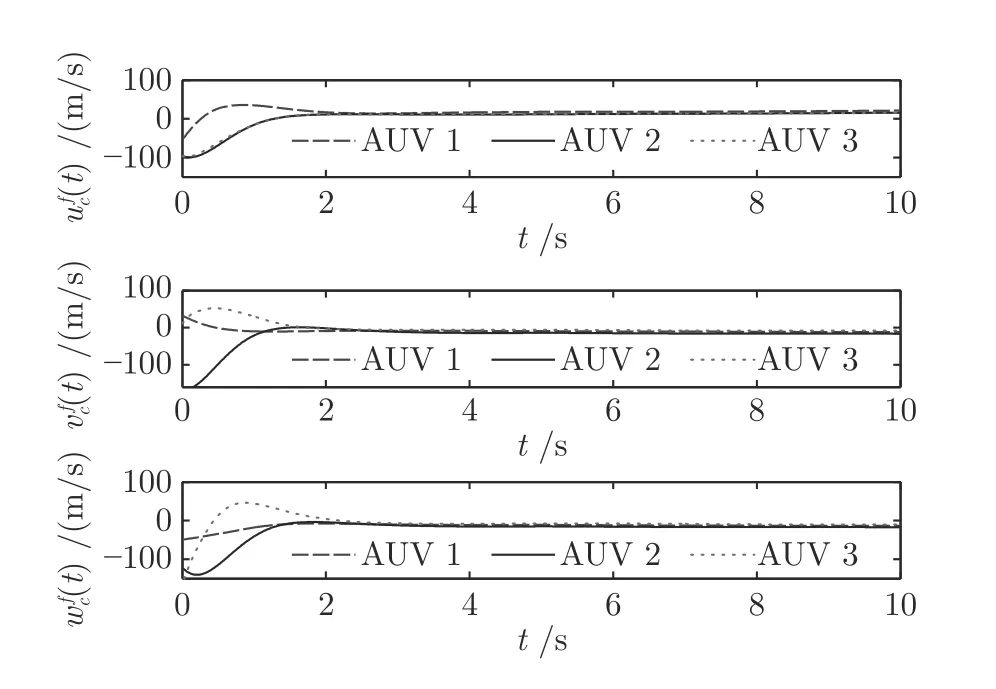
图8 工况 1 下的虚拟控制律Fig.8 The virtual control law under working Condition 1

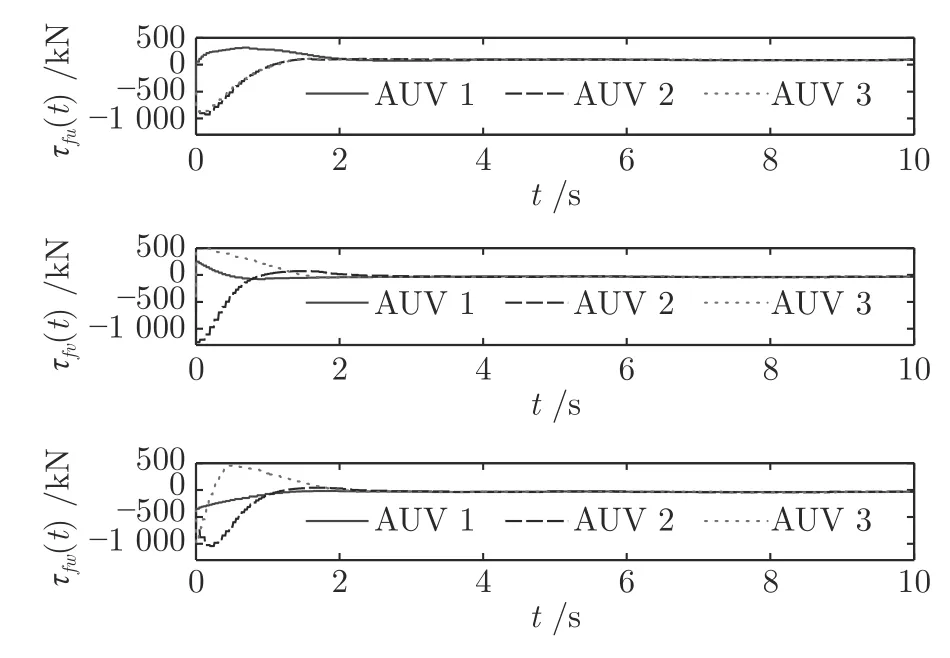
图9 工况 1 下的控制输入Fig.9 The control input under working Condition 1

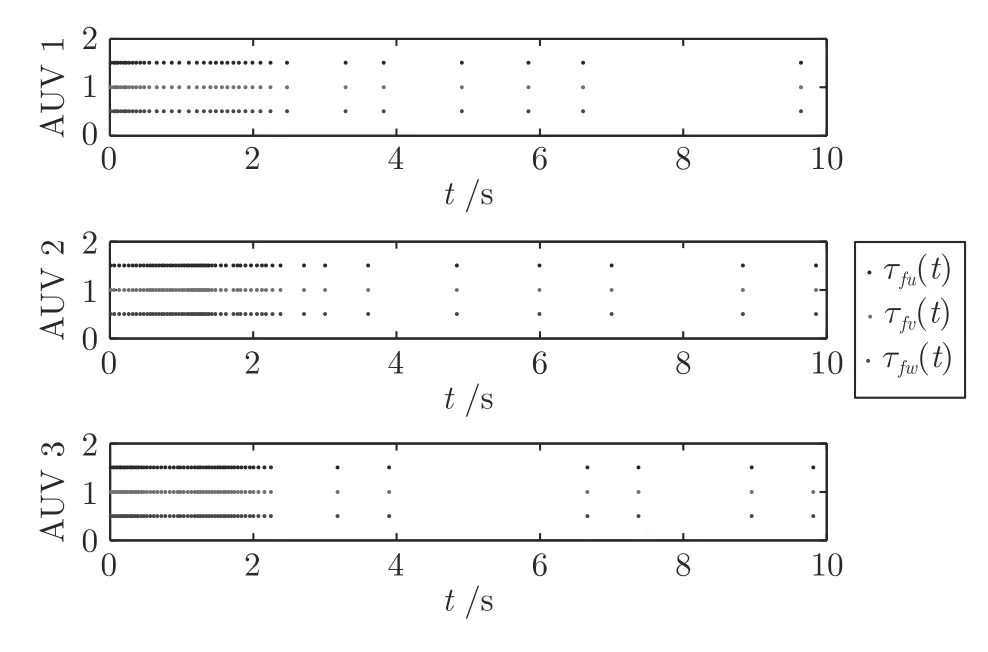
图10 工况 1 下的事件触发时刻仿真图Fig.10 The triggered interval under working Condition 1

为进一步说明基于事件触发通讯机制的编队控制器可节约有限的通信资源等性能,特给出工况1下AUV 1 的控制输入和事件触发时刻仿真图,见图11～ 12 所示.图11 显示连续通信和事件触发通信下跟随AUV 1 的实际控制输入的变化情况,可以看出相比于未引入事件触发的连续控制器c(t),基于事件触发的控制器τf(t)出现分段情况,每一段的开始和结束时刻为AUV 1 的触发时刻,τf(t)在触发时刻更新,在触发时刻之间保持为常数不变,从而减少因不必要的频繁通信造成的资源浪费.由式(37) 生成的事件触发时刻如图12 所示,结合图11 可看出在前2 秒触发间隔较小,2 秒之后控制器逐渐变小,系统逐渐趋于稳定,触发时刻变得稀疏,这与预期的结果一致.说明本文将分布式事件触发引入到AUVs 编队控制中,降低了通信次数和控制器的更新频次,提高了资源的利用率.

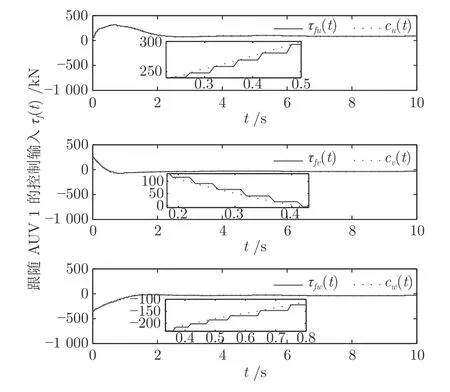
图11 跟随AUV 1 的控制输入τf(t)Fig.11 The control input τ f(t) of AUV 1

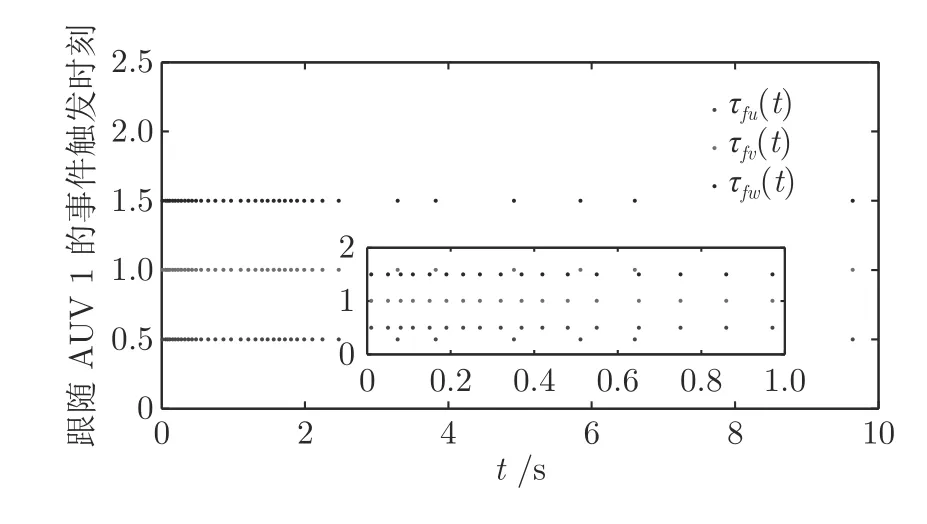
图12 跟随 AUV 1 的事件触发时刻Fig.12 The triggered interval of AUV 1

工况2.为了验证本文算法的正确性且系统收敛时间与初始状态无关,在相同参数条件下对工况2 中任意初始状态(见表1)进行仿真验证,仿真结果见图13～ 17 所示.由图13～ 17 可以看出,在初始状态与期望状态差别较大情况下,本文提出的基于事件触发的AUVs 固定时间编队控制算法的合理性.此外,根据工况1 和工况2 仿真结果验证了本文基于固定时间收敛算法在改善编队系统收敛率的同时其收敛时间与初始状态无关,即在任意不同初始状态下,编队均在2 秒内实现收敛.

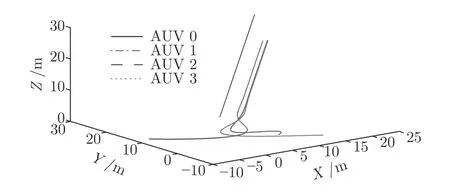
图13 工况2 下的轨迹Fig.13 The trajectory under working condition 2

图14 工况 2 下的位置跟踪误差Fig.14 The position tracking error under working condition 2

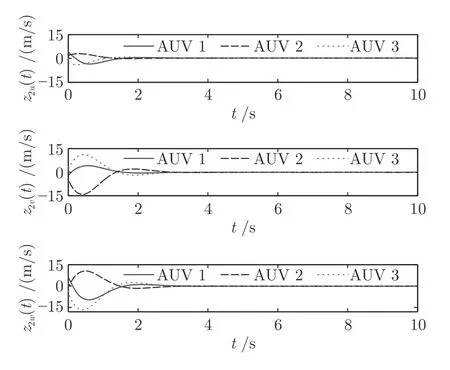
图15 工况 2 下速度跟踪误差Fig.15 The velocity tracking error under working condition 2

图16 工况 2 下的控制输入Fig.16 The control input under working condition 2

综上所述,为了更直观地说明引入事件触发机制节约了通信资源,表2 给出在分布式事件触发机制下,多AUVs 系统在10 秒内控制器的触发次数和触发比率,由表2 数据结合图10 和图17 的不同工况下的触发时刻图以及图11 不同通讯机制的控制器对比,可以看出,本文将事件触发通讯机制引入到多AUVs 编队控制中,降低了AUV 的采样和控制器的更新次数,改进了连续通讯因不必要的通讯造成资源的浪费;在有限网络带宽内,减少信息通讯次数可以降低能耗.显然,本文的基于事件触发控制算法比连续通讯更能节省通讯资源.

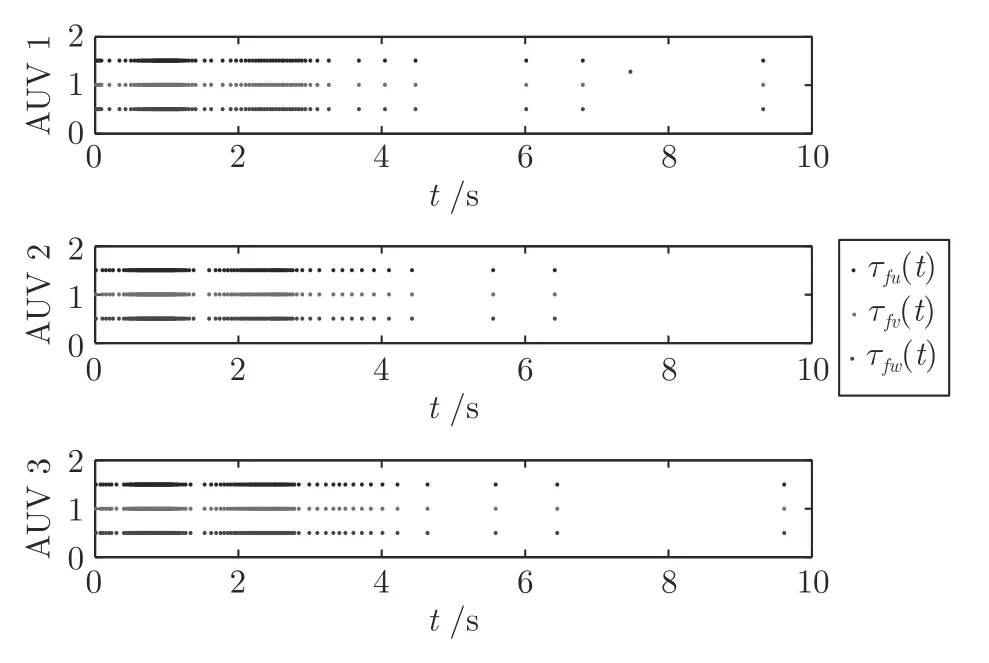
图17 工况 2 下的事件触发时刻仿真图Fig.17 The triggered interval under working condition 2

3.2.2 与比例-积分-微分控制算法的比较

基于工况2 中的AUV 1 给出的初始状态,将本文算法与传统的PID 控制算法进行比较,并给出比例-积分-微分控制算法(Proportional-integralderivative,PID)控制器如下:

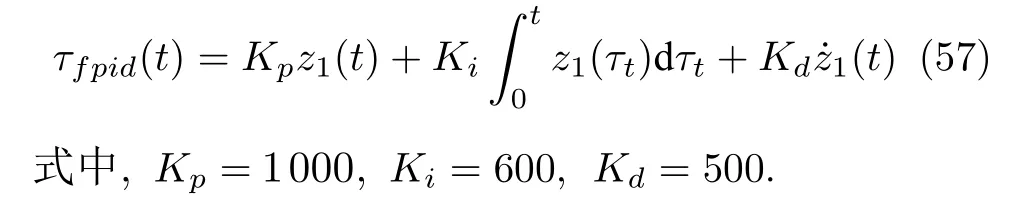
图18～ 19 描述了本文基于事件触发的固定时间控制算法与PID 控制算法下的编队位置跟踪误差和速度跟踪误差比较,由仿真结果可以看出,相比于本文算法,PID 控制算法存在瞬态性能不足,即编队误差在2 秒左右有一个峰值,说明本文所提出的算法不仅加快了编队系统的收敛时间,还具有较好的瞬态性能和稳态性能,可以更好地实现AUVs的编队.此外,表3 通过各个误差信号的均方差D和平均值E给出本文控制算法和PID 算法的一个量化比较结果,进一步直观地验证了本文所提出的算法不仅改善了编队的收敛时间,还提高了系统的控制性能,比PID 算法的系统控制性能更好.

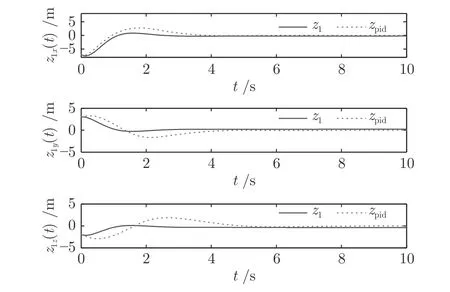
图18 跟随 AUV 1 的位置跟踪误差Fig.18 The position tracking error of AUV 1

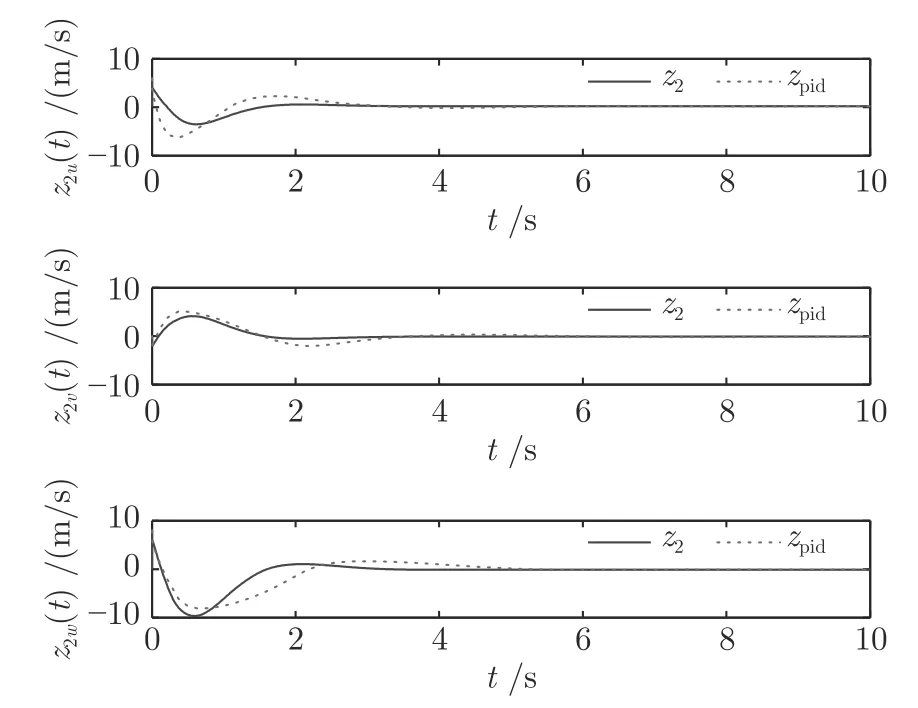
图19 跟随 AUV 1 的速度跟踪误差z2(t)Fig.19 The velocity tracking error of AUV 1

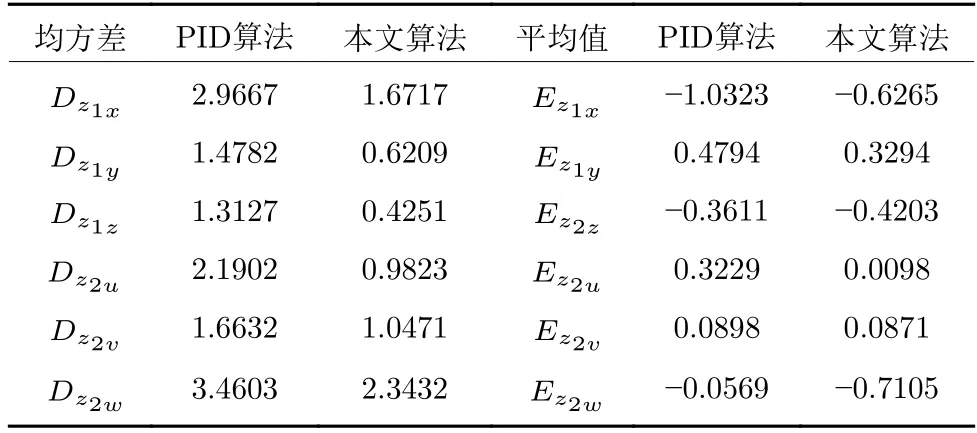
表3 本文算法和PID 算法的比较结果Table 3 Comparison results in the algorithm of proposed in paper and PID

4 结束语

本文提出一种基于事件触发机制的多AUVs固定时间编队控制算法,同时解决了多AUVs 编队系统有限通信资源的限制以及编队收敛速度慢的问题.基于反步动态面控制算法,将分布式事件触发通讯机制引入多AUVs 领航-跟随编队控制策略中,根据固定时间控制理论的思想,构造出事件触发函数,设计出基于事件触发的编队控制器,保证编队系统实现全局固定时间收敛.除了加快系统的收敛速度外,其收敛时间不受初始状态的影响;同时通过减少控制器的更新频次和通信次数,降低系统通信能耗,提高对有限通信资源的利用率.